基于“最近发展区理论”的高中数学教学

湖南省常德临澧县第一中学 石海清

基于“最近发展区理论”的高中数学教学

湖南省常德临澧县第一中学 石海清

“最近发展区理论”简单地将学生的发展水平分为了两类：一方面是现有水平，另一方面则是潜力水平，学生要通过学习从现有水平中挖掘出相应的潜力。在高中数学教学中，这一理论对学生的学习产生了极为积极的现实意义，使不同层次的学生发挥最大的潜能，以期使不同层次的学生达到应掌握的程度。

高三数学；最近发展区理论；目标；终点；潜能

苏联心理学家维果茨基的“最近发展区理论”提出到目前已经快有一百年的时间了，但是这一理论对现代高中数学教学仍具有极为有效的指导作用。在“最近发展区理论”的具体运用中，教师除了要对学生进行较为普遍的基础性教学外，还要在学生能力允许范围之内对学生实施针对性强化教学，以便能够让学生的潜力得到最大限度的发挥，为学生的能力获得更进一步的发展提供必要的保障。

一、基于学生的“最近发展区”来找准学生认知的起点、确定不同层次学生需达到教学的目标

最近发展区理论的提出者——维果茨基说过这样的话：“如果儿童在最近发展区接受新的学习，其发展会更有成果。”我根据多年从事高中数学的教学经验，再结合自己对于“最近发展区理论”的相关认识，对此有了一些属于自己的粗浅理解。

教师要在高中数学教学中运用“最近发展区理论”来促使学生进行“新的学习”，而这个所谓“新的学习”是由两个部分组合构成的，一是旧知识的认知起点；二是新知识的学习过程，借此来为学生的学习提供必要且有用的帮助。学生在对高中数学的学习过程中，凭自己的力量来得到的学习收获是极为有限的，其学习的效果受到自身学习能力的影响，如对知识的熟练程度、对相关知识的理解程度、对学习要点的把握程度等，可视作新知识发展的起点。因此，学生要想在学习中获得较为明显的效果，就需要依靠教师的不断引导，这样学生才能对所学的知识有着较为全面的理解，从而尽可能地将其中有用的部分进行吸收。

特别是对于处于高三阶段的学生而言，其进行数学学习的目标其实最为明确，就是要将数学基础知识掌握牢固，并尽最大可能得到数学综合能力的拓展，以便能够在不久后的高考中获得不错的成绩，从而使自身的价值得到充分的体现，并为日后的学习奠定良好的基础。正是基于这样一些因素，教师应当依据“最近发展区理论”的相关指导，在教学中尽可能地采取能够提高学生数学综合能力的教学方法，以不同层次学生认知的起点，高考为高三学生数学学习的最终目标，来对整个高三的数学教学进行较为合理的安排。

二、基于学生的“最近发展区”来对教学的终点进行确定

按照一般的教学理论，教学其实是一个永无止境的过程，在教学中永远都是没有最好只有更好。我们在这里需要将教学的范围进行适当的缩小，因为主要是对高三数学教学进行较为深入的讨论，所以这样的一个教学过程是存在一定终点的，其终点就是学生的最大潜能得到充分的发挥，使学生的能力水平达到理论的最高值。而在这一个教学终点的确定过程中，教师需要在“最近发展区理论”的指引下保证教学工作的顺利开展。

高中数学教师要对教材中的“最近发展区”进行升入挖掘，以便能够激发学生对数学学习的热情，从而构建起一定的数学知识体系。就平常的课堂教学而言，教师在教学中大多会以教材的例题进行讲学，这样做是有一定好处的，由于解答过程简单及教学思路清晰，使得学生能够较为容易地听懂例题教学。但是正是由于例题的简单，使得学生的学习过程显得过于平淡无奇，学生无法提起对数学学习的兴趣，从而使得学生的数学学习热情被削弱，进而使学生无法进行积极有效的学习。如果此时教师能够从“最近发展区”的角度出发，积极努力地寻求学生学习中的平衡点，这样就可以让学生的思维重新活跃起来，从而更为积极地对数学的相关问题进行思索及探究，这样就让学生在不知不觉间构建起了较为完善的数学知识系统化结构，进而使学生的潜能发挥变得更为容易，让学生的能力水平无限趋近于理论的最高值。

同时，教师还需要在高三数学的教学中对学生的学习施以必要的引导，以便能够合理地运用数学思考题来进行“最近发展区”的创设，从而有效缓解教学中上下衔接不畅的不良现象。在这样一个过程中，教师可以通过一定的教学经验对教材进行全面深入的了解，从而发现教材内的相互关联，并提出相应的问题来让学生进行思考，以便能够对学生进行由此及彼的有效引导，使学生能够在新课程的学习前对已学过的课程进行回顾，从而更为有效地去进行接下来的学习，以求其能够尽最大可能地将自己的最大潜能予以发挥，进而在教学中让学生获得的数学综合能力保持在尽可能高的水平之上。

三、基于“最近发展区”使不同层次的学生通过教师的指引达到相应的更高的层次，最终使各自的潜能尽情发挥、从而达到高考的要求

如函数与导数是选修2－2的内容，要求学生掌握函数的概念、函数的性质（主要是在必修1）、导数的概念、导数的几何意义、导数与函数的单调性（主要内容是在选修2－2）以及函数与导数的运用（高考要求能灵活运用）。我充分选择经典例题，发挥一题一灯的作用、照顾彼此，布置满足不同层次学生的题型练习，分类指导、逐渐带动。

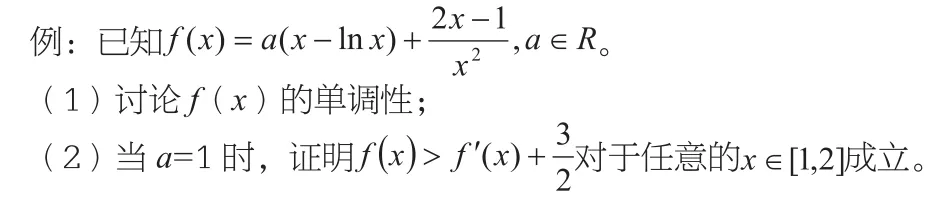
第（1）题可以请基础差的学生上台写函数的定义域，求导函数，请中等生上台继续完成分析单调性，然后在大家都弄懂的基础上完成第（1）问；第（2）问请基础好的学生说自己的解题思路，老师根据他们提供的思路带领大家演算，寻找最佳解题方案和途径，第（2）问蕴含的重要数学思想方法和实施技巧也能激发中等层面学生的学习兴趣，带动下层同学跃跃欲试的潜能。

总之，在高三阶段的数学学习中，基于“最近发展区理论”的教学指引，为了使学生能够在教学中获得更好的发展，有必要对学生进行差异化对待，以便让处于不同能力层次的学生均能得到有效的发展。

在具体教学中，教师需要注意的就是，要让学生能够接受有效的数学知识教学，从而让学生能够通过教学做到“低进高出、高进优出、优进特出”，即教师在正式进入教学前为了便于管理，将学生按学习潜能及基础知识掌握程度的不同进行了简单的分组，然后通过基于“最近发展区理论”的教学来使学生的能力层次上升一层，从而使学生的潜能能够得到最大程度的释放。

总而言之，在高中数学，特别是高三年级的数学教学中，教师一定要能够将“最近发展区理论”搞懂、搞透，从而将其对教学的促进作用发挥到极致，从而使学生的学习潜能能够得到最大限度的挖掘，进而让学生能够从容不迫地面对即将来临的重要转折——高考。