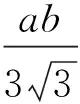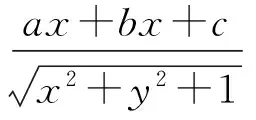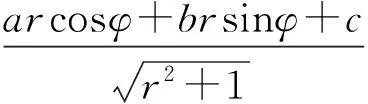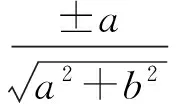浅谈多元函数极值的判定

余小飞，李 平

(河南工业职业技术学院，河南 南阳 473000)



浅谈多元函数极值的判定

余小飞，李 平

(河南工业职业技术学院，河南 南阳 473000)

根据多元函数极值的判定定理，研究多元函数极值的求解方法。

多元函数极值判定

1 多元函数极值的定义

若函数f(P)=f(x1,x2,…,xn)在点P0的领域内有定义，并且当0<ρ(P0,P)<δ时，f(P0)>f(P)或f(P0)

2 极值存在的充分条件

若函数f(P)在点P0处满足：(1)df(P0)=0，d2f(P0)<0时，函数f(P)在点P0处取得极大值；(2)df(P0)=0，d2f(P0)>0时，函数f(P)在点P0处取得极小值．

特别的，对于二元函数f(x,y)，设A=f″xx(x0,y0)，B=f″xy(x0,y0)，C=f″yy(x0,y0)，当D=AC-B2≠0时：(1)若D>0，A>0(C>0)，此时函数取得极小值；(2)若D>0，A<0(C<0)，此时函数取得极大值；(3)若D<0，此时函数的极值不存在．

3 案例分析

显然z的极值均为u的极值；且u在点(x,y)取得的极值不为零时，z也在点(x,y)取得极值；且u在点(x,y)取得的极值为零时，须进一步讨论．

解方程组

由于z在点P0附近变号，所以z(P0)不是极值.计算二阶偏导数：

解析另x=rcosφ，y=rsinφ，则

解方程组

(1)

(2) ，

先设a、b不同时为零.由(2)考虑到r=0不是解(r=0，不论φ为何值，都不满足(1)式)，故有asinφ=bcosφ.于是

设c=0，由(1)式有acosφ+bsinφ=0，再由(3)式得，a=b=0，这与a、b不同时为零矛盾，因此当c=0时无解．

为保证r>0，在cosφ与sinφ前取与c一致的符号，因此有

[1]费定辉，周学圣.数学分析习题集题解[M]．济南：山东科学技术出版社，2008：368-369．

[2]乐春红.关于二元二次函数极值的一点思考[J]．重庆工商大学学报：自然科学版，2009，26(4)：334-336．

[3]杨元超，张守贵.二元泰勒展开式在求解函数极限中的应用[J]．重庆工商大学学报：自然科学版，2013，30(10)：25-27．

(编辑 赵欣宇)

Discussion on the Judgment Theorem of Extremum of Multivariate Function

YU Xiaofei, LI Ping

(Henan Polytechnic Institute, Nanyang 473000, China)

According to the judgment theorem of extremum of multivariate function, this paper studies the method of solving the extremum of multivariate function．

judgment of extremum of multivariate function

2017-03-16

余小飞(1986-)，理学硕士，讲师。主要研究方向：基础数学。

G712

A

1672-0601(2017)07-0118-02