基于电容电压前馈的LCL逆变器并网控制

李锐，邓磊，李小谦，徐正喜，刘邦银

（1.武汉第二船舶设计研究所，湖北 武汉 430000；2.强电磁工程与新技术国家重点实验室，湖北 武汉 430000）

基于电容电压前馈的LCL逆变器并网控制

李锐1，邓磊1，李小谦1，徐正喜1，刘邦银2

（1.武汉第二船舶设计研究所，湖北 武汉 430000；2.强电磁工程与新技术国家重点实验室，湖北 武汉 430000）

并网逆变系统中，LCL滤波器相比单电感滤波器具有更优的滤波性能，然而引入了谐振点，降低了系统稳定性。揭示了存在数字延时LCL型并网逆变器逆变侧电流单环控制的稳定性恶化现象，提出了一种基于电容电压前馈的逆变侧电流控制方案，该方案通过电容电压前馈使系统降阶，从而有效地改善了系统的稳定性，同时分析了延时和前馈系数对电容电压前馈效果的影响。所提控制方案的有效性在自行研制的630 kW三相逆变器上得到了实验验证。

并网逆变器；LCL滤波器；电容电压前馈；数字延时

LCL型滤波器因为对高频分量具有更高的衰减能力，在工业产品中得到广泛的应用。但与此同时，LCL滤波器本身存在的谐振峰会造成并网逆变器的失稳，因此如何保证LCL型并网逆变器稳定运行成为一个关键的技术问题。许多文献中相继提出了无源阻尼和有源阻尼的方案来抑制LCL滤波器的谐振峰，从而实现系统的稳定。

无源阻尼的方案主要是在滤波电感或电容上并联或串联电阻，增加滤波器本身的阻尼，从而消除谐振峰对系统的影响［1］。然而电阻上会引入额外的损耗，并且会降低LCL滤波器对高频谐波的衰减能力。

针对无源阻尼增加系统损耗的缺点，相应的有源阻尼方案相继提出。有的学者通过额外引入电容电压或电容电流来实现有源阻尼［2-7］。以电容电流作为反馈增加1个内环控制，等效为在LCL滤波器电容上并联1个电阻，增加了系统的阻尼，可以有效地抑制谐振峰。有些文献考虑到增加1个电流采样霍耳代价较高，改为采样电容电压，利用电容电压微分来代替电容电流采样作为内环反馈，实现系统阻尼。但是采用电容电压微分容易放大系统中的高频扰动。还有学者同时采样逆变器侧电感电流和并网电流进行控制［8-12］。文献［8-9］采用逆变侧电流作为反馈，而用电网电流和电网电压作为前馈，实现三阶系统降阶。文献［10-12］中将逆变器侧电流和并网电流进行加权求和作为反馈，通过调整加权系数匹配LCL滤波器前后电感比，将三阶滤波器降阶为一阶，从而消除谐振峰的影响。这两种控制策略对电路参数较为敏感，参数匹配不当则不能实现完全的降阶。

在上述的文献中，均没有考虑到数字控制的特殊问题，即数字延时的影响。文献［13-16］考虑了数字控制1拍滞后的影响，从而发现并网逆变器采用网侧电流单环控制时，仅仅采用简单PΙ控制器也可以实现系统稳定。文献［16］发现当考虑1拍滞后时，只要逆变器LCL谐振频率和控制频率之比在一定范围内，就可以保证系统的稳定。文献［17］在此基础上，分析了考虑1拍滞后系统PΙ控制器参数的设计方法。文献［18］则提出了优化数字延时的网侧电流单环控制方法。

本文基于数字控制的特点，分析了存在数字延时条件下，逆变器并网控制稳定性上的特殊问题，发现逆变侧电流控制随着延时增加而逐渐失稳，给出了保证系统稳定的延时范围。进一步通过分析发现增加电容电压前馈，可以将逆变侧电流控制的并网逆变器系统降阶为一阶系统，从而消除谐振峰对系统稳定性的影响。并分析了数字延时以及前馈系数对电容电压前馈降阶效果的影响。最后通过实验验证了控制器参数设计的有效性。

1 数字延时对稳定性影响分析

图1所示为一个采用逆变侧电感电流控制的LCL型三相并网逆变器的系统结构图。三相并网逆变器采用坐标系变换，将abc三相坐标系的电量关系转换到dq旋转坐标系下实现相应的控制算法。本节详细分析延时对逆变侧电感电流控制策略稳定性的影响。

图1 逆变侧电流控制的并网逆变器Fig.1 The grid-tied inverter with inverter-side current control

将数字控制中的延时成分考虑进去，考察延时对逆变侧电感电流控制系统稳定性的影响，考虑延时后系统的控制框图如图2所示。

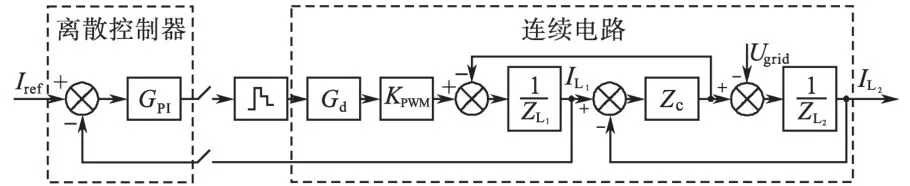
图2 考虑延时的逆变侧电感电流控制框图Fig.2 The block diagram of inverter-side inductive current control considering digital delay

图2中数字延时环节用Gd表示，当系统中存在延时Td时，延时环节表达式为

这里使用广义z变换来实现对含有纯延时系统的离散，这样离散化后的系统开环传递函数为

式中：Tc为控制周期；Kp为比例系数；Ki为积分系数；L1为逆变侧电感；L2为网侧电感；Cf为滤波电容。

系统参数为：LCL滤波器Linv=0.15 mH，Cf= 200 μF（Δ），Lg=0.15 mH，电网电压Ug=220 V（RMS），直流电压Udc=800 V，控制频率fc=2.5 kHz，控制器参数Kp=0.3，Ki=75。可以分析延时对这样一个系统稳定性能的影响。图3所示为延时分别为1Tc,2Tc,3Tc和4Tc时系统的开环波特图。

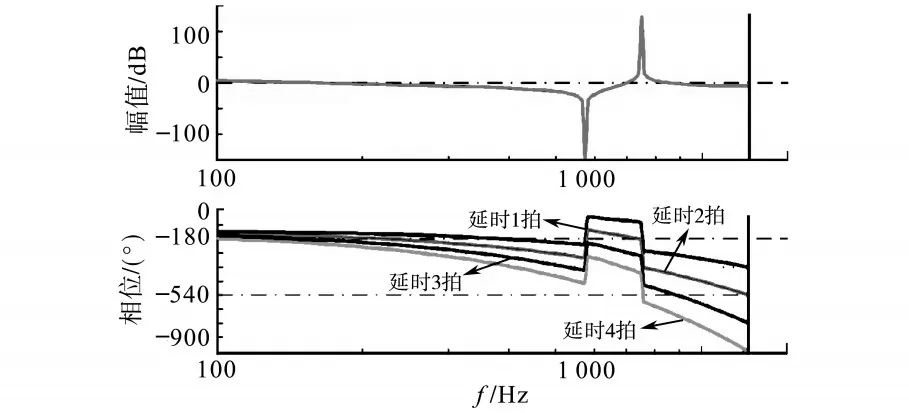
图3 不同延时下系统开环波特图Fig.3 The bode figure of open-loop transfer function with different digital delay

图3中可以看到，当存在1拍的延时后，系统稳定性被破坏，正谐振峰处的相位由于延时存在而被拉低，穿越了-180°，导致系统失去稳定；当延时进一步增大，相位穿越-180°的点被迁移到了负谐振峰段，使得系统又重新获得了稳定；然而随着延时再次增加，系统在控制器截止频率之前就穿越了-180°，系统将不再稳定。

从上述分析可以发现，采用逆变侧电感电流控制时，需要尽可能减小数字控制系统带来的延时，从而保证系统稳定性，若数字延时较大，逆变侧电流控制将失去其稳定性。然而实际数字系统可能由于AD采样过程和PWM调制过程带来的固有延时已经使系统的稳定裕度很小，甚至已经使系统失稳，因此需要考虑其他的方法来增加系统的稳定性能。

2 电容电压前馈的降阶特性

2.1 理想电容电压前馈的降阶特性

电容电压前馈一方面可以很好地抑制电网电压扰动的影响，另一方面同时也改变了系统本身的传递函数，对系统稳定性以及动态性能都会带来很大的影响。图4所示为增加电容电压前馈后的系统框图。

图4 增加电容电压前馈后系统框图Fig.4 The block diagram of LCL filter with capacity voltage feed-forward

图4中，k为电容电压前馈系数，Tdv为延时时间，这样增加前馈后的系统传递函数变为

当k为1，Tdv为0时，即电容电压前馈认为是一个理想的单位前馈，此时Gvc(s)=0，从图4中可以看出就实现了电容电压的解耦，系统传递函数变成：

图5给出了当控制系统存在1拍延时时，采用理想电容电压前馈后与无前馈的系统开环传函数的波特图，可以看到电容电压前馈将LCL型滤波器降阶成了单L滤波器，从一个三阶的振荡系统降阶到了一阶的系统，这样系统就不存在由于谐振峰带来的稳定性问题了。因此电容电压前馈可以非常有效地改善逆变侧电感电流控制系统的稳定性。从物理概念上我们可以这样理解理想电容电压前馈的系统降阶效果：电容电压中含有系统的所有谐振分量信息，将电容电压中的谐振分量直接前馈到逆变器输出电压后，前级电感两端电压的谐振分量就相互抵消，从而使系统不再含有谐振峰，实现了系统的降阶。

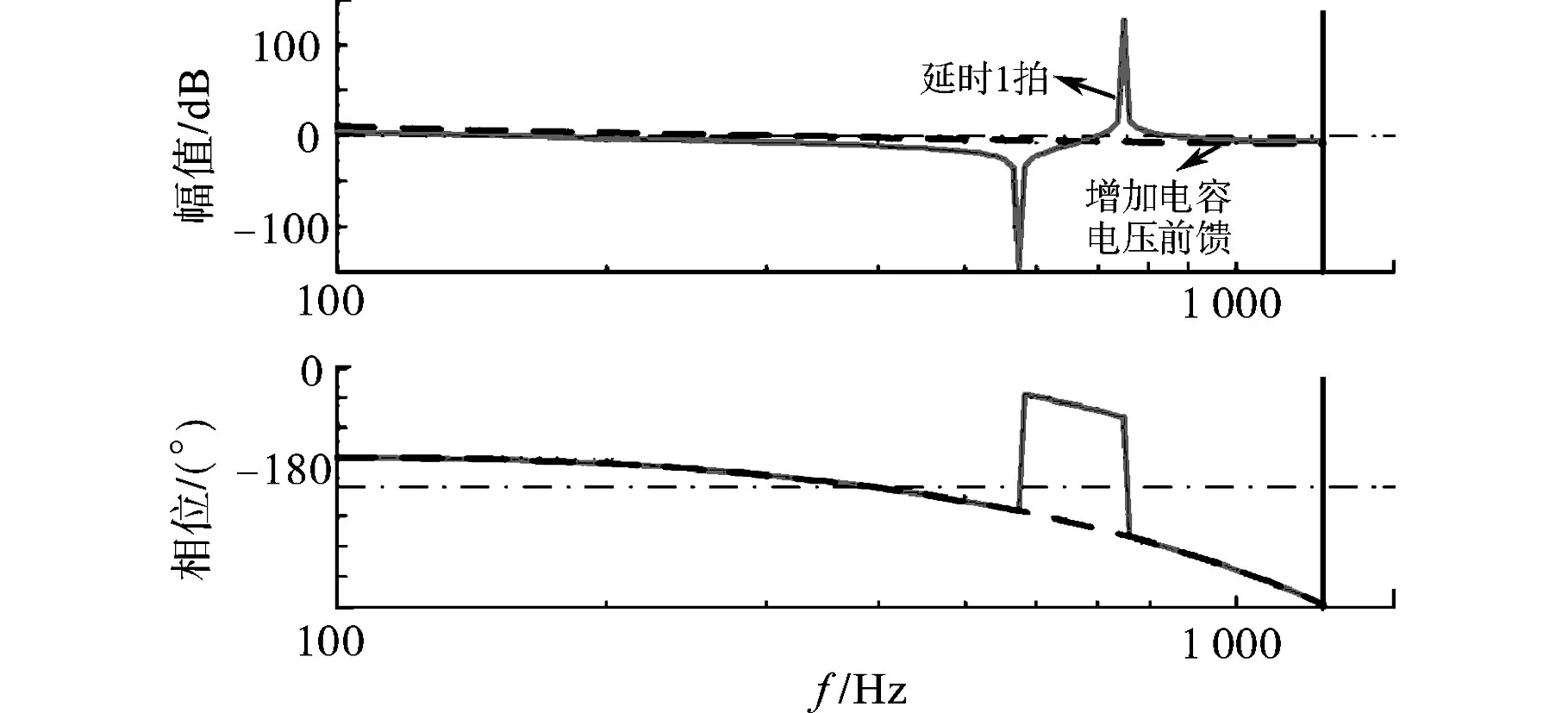
图5 增加电容电压前馈前后开环波特图对比Fig.5 The compare of open-loop bode figures with capacitive voltage feed-forward and without

2.2 数字延时对电容电压前馈影响

理想电容电压前馈会使系统降阶，可以非常明显地改善系统的稳定性。然而实际控制过程中很难做到理想的电容电压前馈，一方面数字控制器在采样电容电压量并前馈到输出控制量的过程中必然存在一定的延时，另一方面直流侧电压变化后前馈系数也相应变化，并不是恒定为1。前馈系数和延时都会影响到前馈控制的效果，首先讨论延时对电容电压前馈控制性能的影响。

图6 前馈通道不同延时的开环波特图Fig.6 The open-loop bode figures with different delay in feed-forward

图6给出了理想前馈和系统前馈通道分别为0.5拍、0.75拍和1拍延时条件下的系统开环波特图。从开环波特图可以看到滞后0.5拍时系统已经接近临界稳定的状态，并且随着滞后时间的增加，系统会趋于不稳定。而延迟越小谐振峰也越小，系统也越稳定。从物理概念上可以理解为：延迟时间使得前馈到逆变器输出电压中的谐振分量相位发生了偏移，从而前级电感两端电压的谐振分量不能完全抵消为零，当延迟越大相位偏移也越大，谐振分量也相应越大。当延时导致相位发生180°偏移时，前馈反而会导致前级电感两端压降中谐振分量增加1倍，对系统稳定起反作用。

2.3 前馈系数对电容电压前馈影响

考虑实际控制中总是存在一定的延时，这里取延时为0.5拍。改变前馈系数k，从图7所示的不同前馈系数下系统的开环波特图可以看到，随着前馈系数的减小谐振峰逐渐提高，系统趋于不稳。从阶跃响应可以看到随着前馈系数减小，超调逐渐减小，前馈系数为1时，超调量约为90%，前馈系数为0.6时，超调量约为70%。然而随着前馈系数减小，前馈效果减弱，系统稳定性变差，从图8中可以看到，前馈系数为1时，系统发生阶跃后，振荡会迅速大幅度衰减，振荡频率很低，具有明显的收敛稳定过程；而前馈系数为0.6时，系统会较长时间振荡，收敛速度慢，且振荡频率变高，趋向于谐振段频率，说明系统稳定性降低了。

图7 不同前馈系数时的开环波特图Fig.7 The open-loop bode figures with different feed-forward factor

图8 不同前馈系数时的阶跃响应Fig.8 The step responses with different feed-forward factor

3 实验验证

在一台630 kW三相光伏并网逆变器上进行电容电压前馈逆变侧电流控制方案实验验证，该逆变器具体参数与系统参数相同。需要注意的是，由于实验室条件限制，无法实现以额定功率接入电网进行实验，而是采用了1个环形对拖的测试平台进行实验。测试平台以1台变频器作为电压源模拟电网，逆变器并联到变频器的输出侧，逆变器直流侧与变频器直流侧并联。由于变频器输出侧也有很大的滤波电感，相当于逆变器输出的网侧电感加大，约有0.8 mH，等效的谐振频率约在600 Hz附近。

图9 不同数字延时的实验结果Fig.9 The experimental results with different delay

图9、图10分别给出了逆变器不同数字控制延时和前馈通道延时下的静态波形和采用不同前馈系数进行控制的系统静态和动态输出波形。测试时输出电流为1 000A峰值，输出线电压为310V。底部为实时检测的电流频谱分析。可以看到，当反馈和前馈延时均为0.25拍时，因为反馈本身延时较小，前馈相对较理想，此时的控制效果最佳，系统具有较好的谐振抑制效果，并网电流THD含量为2.4%。当反馈延时增加到0.5拍后，谐振段谐波有所增加，符合前面所得到的逆变侧电流控制中延时会加剧系统稳定性的分析结果；此时因为前馈控制对系统降阶效果较理想，反馈延时增加对稳定性减弱的效果不是很明显，该条件下并网电流THD含量为2.5%。当前馈延时也增加到0.5拍后，前馈的降阶效果被削弱，波形上可以看到谐振段谐波进一步加剧，出现了明显的振荡，系统稳定性进一步减弱，电流THD达到了3.9%，这和前述的理论分析是吻合的。

图10 不同前馈系数的实验结果Fig.10 The experimental results with different feed-forward factor

图10给出了在反馈和前馈延时均为0.25拍条件下，采用不同前馈系数进行控制的系统静态和动态输出波形。可以看到由于本身控制延时小，不同的前馈系数均能保证系统稳定，前馈系数对系统静态特性影响不明显。2种前馈系数下动态响应上则存在差异，实验条件为系统电流指令从200 A峰值阶跃至600 A峰值。前馈系数为1时，系统指令跳变后第1个最大峰值电流为780 A，超调约有45%，且第2个波峰即已调节至600 A，整体调节时间小于10 ms。而前馈系数为0.6时，系统指令跳变后第1个最大峰值电流为680 A，超调约有20%，且第2个波峰仍为680 A，直至第3个波峰才调节至600 A，整体调节时间为20 ms。这个实验结果表现的趋势和前述关于前馈系数对动态特性影响的理论分析也是吻合的。由于逆变系统是基于正弦量阶跃而非直流量阶跃，因此超调量和调节时间数值上与图8存在一定差异。

4 结论

本文主要分析了延时对LCL型并网逆变器逆变侧电流控制稳定性的影响，分析发现延时越大，该控制方案下系统稳定性越差。同时发现采用电容电压前馈的方案可以使系统降阶，从而有效地改善系统的稳定性。前馈通道不同的延时和前馈系数对系统稳定性以及动态特性均有影响，延时越大，前馈系数越小，稳定性越差。

［1］Liserre M，Blaabjerg F，Hansen S.Design and Control of anLCL-filter-based Three-phase Active Rectifier［J］.IEEE Trans⁃actions on Industry Applications，2005，41（5）：1281-1291.

［2］Guoqiao S，Dehong X，Luping C，et al.An Improved Control Strategy for Grid-connected Voltage Source Inverters with an LCL Filter［J］.IEEE Transactions on Power Electronics，2008，23（4）：1899-1906.

［3］Prodanovic M，Green T C.Control and Filter Design of Three-phase Inverters for High Power Quality Grid Connection［J］.IEEE Transactions on Power Electronics，2003，18（1）：373-380.

［4］Guohong Z，Rasmussen T W，Lin M，et al.Design and Control of LCL-filter with Active Damping for Active Power Filter［C］∕∕in：Proc.of Industrial Electronics（ISIE），2010 IEEE Interna⁃tional Symposium on.Bari，2010：2557-2562.

［5］Erika T，Holmes D G.Grid Current Regulation of a Three-phase Voltage Source Inverter with an LCL Input Filter［J］.IEEE Transactions on Power Electronics，2003，18（3）：888-895.

［6］Dannehl J，Fuchs F W，Hansen S，et al.Investigation of Active Damping Approaches forPI-based CurrentControlof Grid-connected Pulse Width Modulation Converters with LCL Filters［J］.IEEE Transactions on Industry Applications，2010，46（4）：1509-1517.

［7］王亮，王志新，陆斌峰.基于Park变换的单相光伏并网控制研究［J］.电气传动，2015，45（6）：37-40.

［8］Petrella R，Revelant A，Stocco P.A Novel Proposal to Increase the Power Factor of Photovoltaic Grid-connected Converters at Light Loads［C］∕∕in：Proc.of Universities Power Engineering Conference（UPEC），2009 Proceedings of the 44th Internation⁃al，Glasgow，2009：1-5.

［9］Malinowski M，Kazmierkowski M P，Szczygiel W，et al.Simple Sensorless Active Damping Solution for Three-phase PWM Rectifier with LCL Filter［C］∕∕in：Proc.of Industrial Electron⁃ics Society，2005.IECON 2005.31st Annual Conference of IEEE.Raleigh，NC，2005：5.

［10］Guoqiao S，Xuancai Z，Min C，et al.A New Current Feedback PR Control Strategy for Grid-connected VSI with an LCL Filter［C］∕∕in：Proc.of Applied Power Electronics Conference and Exposition，2009.APEC 2009.Twenty-fourth Annual IEEE.Washington DC，2009：1564-1569.

［11］Guoqiao S，Xuancai Z，Jun Z，et al.A New Feedback Method for PR Current Control of LCL-filter-based Grid-connected In⁃verter［J］.IEEE Transactions on Industrial Electronics，2010：57（6）：2033-2041.

［12］沈国桥，徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制［J］.中国电机工程学报，2008，28（18）：36-41.

［13］Qiang Z，Lewei Q，Chongwei Z，et al.Study on Grid Connected Inverter Used in High Power Wind Generation System［C］∕∕in：Proc.of Industry Applications Conference，2006.41st IAS Annual Meeting.Conference Record of the 2006 IEEE.Tampa，FL，2006：1053-1058.

［14］Teodorescu R，Blaabjerg F，Liserre M，et al.A Stable Three-phase LCL-filter Based Active Rectifier Without Damp⁃ing［C］∕∕in：Proc.of Industry Applications Conference，2003.38th IAS Annual Meeting.Conference Record of the.2003，3：1552-1557.

［15］仇志凌，杨恩星，孔洁，等.基于LCL滤波器的并联有源电力滤波器电流闭环控制方法［J］.中国电机工程学报，2009，29（18）：15-20.

［16］Dannehl J，Wessels C，Fuchs F W.Limitations of Voltage-ori⁃ented PI Current Control of Grid-connected PWM Rectifiers with LCL Filters［J］.IEEE Transactions on Industrial Elec⁃tronics，2009，56（2）：380-388.

［17］Jinjun Y，Shanxu D，Bangyin L.Stability Analysis of Grid-connected Inverter with LCL Filter Adopting a Digital Single-loop Controller with Inherent Damping Characteristic［J］.IEEE Transactions on Industrial Informatics，2013，9（2）：1104-1112.

［18］李锐，殷进军，刘邦银，等.基于LCL滤波的光伏逆变器网侧电流单环控制［J］.电力电子技术，2013，（3）：62-64.

Grid-tied Control of LCL Inverter Based on Capacitive Voltage Feed-forward

LI Rui1，DENG Lei1，LI Xiaoqian1，XU Zhengxi1，LIU Bangyin2
（1.Wuhan Second Ship Design and Research Institute，Wuhan 430000，Hubei，China；2.State Key Laboratory of Advanced Electromagnetic Engineering and Technology，Wuhan 430000，Hubei，China）

LCL filter for smoothing grid current of PV inverter is better than simple L-filter.However，there is possible instability of the LCL filter system caused by the zero impedance at the resonance frequency.The stability degradation phenomenon of the inverter with inverter side current control with increasing of digital delay was revealed.Then inverter side current control scheme based on capacitive voltage feed-forward was proposed.The inverter side current control scheme based on capacitive voltage feed-forward realized the reduction of system order by the feed-forward of capacitance voltage and effectively improved the stability of system.Then the influences of digital delay and feed-forward coefficient on the stable effect of capacitance voltage feed-forward were analyzed in detail.The effectiveness of the control strategy is verified by experimental results in a 630 kW three-phase grid-tied inverter.

grid-tied inverter；LCL filter；capacity voltage feed-forward；digital delay

TM431

A

10.19457∕j.1001-2095.20170708

2016-05-16

修改稿日期：2016-07-27

李锐（1987-），男，博士，Email：learoylr@163.com