一种基于Logistic回归的银行保险消费行为影响因素分析与预测

于洪霞, 李 兴

(1.上海电力学院 数理学院, 上海 201300; 2.华泰财产保险有限公司 个险承保部, 上海 201315)



一种基于Logistic回归的银行保险消费行为影响因素分析与预测

于洪霞1, 李 兴2

(1.上海电力学院 数理学院, 上海 201300; 2.华泰财产保险有限公司 个险承保部, 上海 201315)

运用Logistic回归方法分析了银行保险消费行为的影响因素,并构建了预测模型,然后利用保留样本进行了实证检验.通过对样本数据过离散、空单元、多元共线性、特异值、特殊影响案例的诊断,以及对模型的拟合程度和预测效果的检验,验证了所构建的模型具有较好的拟合程度和预测效果.

银行保险; 消费行为分析; 分类变量; Logistic回归分析

随着经济的发展、人们收入水平的提高以及高新技术的普及,广大保险消费者的消费需求日趋复杂多样,对保险产品不仅要求有充足的保障功能,还需要提供周到完善的服务,对保险产品的购买渠道、投保和后续服务的方式也提出了多样化、个性化的需求.保险企业要通过产品和服务为消费者创造出值得回忆的美好体验,需要加强消费者行为研究,了解和掌握消费者的行为活动特点,为保险产品/服务和主题体验设计提供依据.

国内外研究人员已经对银行保险消费者行为开展了各种研究,例如:KARL Borch[1]按照购买动机对保险需求进行了分类,并研究了不同保险需求的决策方式;KUUSELA A H和SPENCE M T[2]对消费者如何选择保险产品进行了研究,并将消费者进行了分类,分析了消费者在决策过程中如何进行信息的排除和选择,进而如何选择不同的消费策略;万晴瑶[3]研究了人口、家庭结构变化对寿险消费需求的影响.对银行保险的研究可参考文献[4]和文献[5].桂林[6]设计了银行保险消费行为调查问卷,并在重庆市开展了调查,运用Logistic模型对调查问卷的数据进行了分析,建立了重庆市银行保险消费者购买模型.中国工商银行上海市分行课题组[7]分析了客户金融消费行为的影响因素和行为特征.

对消费者行为的研究需要大量可信的数据作为基础.目前的研究或从宏观角度出发,或以调查问卷的形式,尚未对银行客户保险消费的数据进行深入的统计分析和研究.为进一步深入分析银行客户保险消费的影响因素并构建预测模型,本文对一个零售银行消费数据库的数据进行了研究.该数据库涉及范围广,存储数据量大,可以满足研究需要.然后将Logistic回归分析方法[8-9]引入银行客户保险消费的统计分析研究中.从消费数据中选择了16个因素,运用Logistic回归分析方法,分析这16个因素与客户保险购买行为之间的关系,然后建立了预测模型并用实证进行检验.

1 数据来源及样本数据诊断

1.1 数据来源

本文数据来自于文献[10]中的案例数据,是一个零售银行的消费数据,共包括32 264条记录,47个变量.

首先,筛选出记录完整、无空单元的数据,共20 878条.选取前12 000条,将是否购买保险作为因变量,选取其中的16个自变量进行影响因素分析,并构建预测模型.在剩余的数据中选择5 000条作为保留数据,进行模型检验.

16个自变量定义如表1所示.训练样本数据统计结果如表2所示.

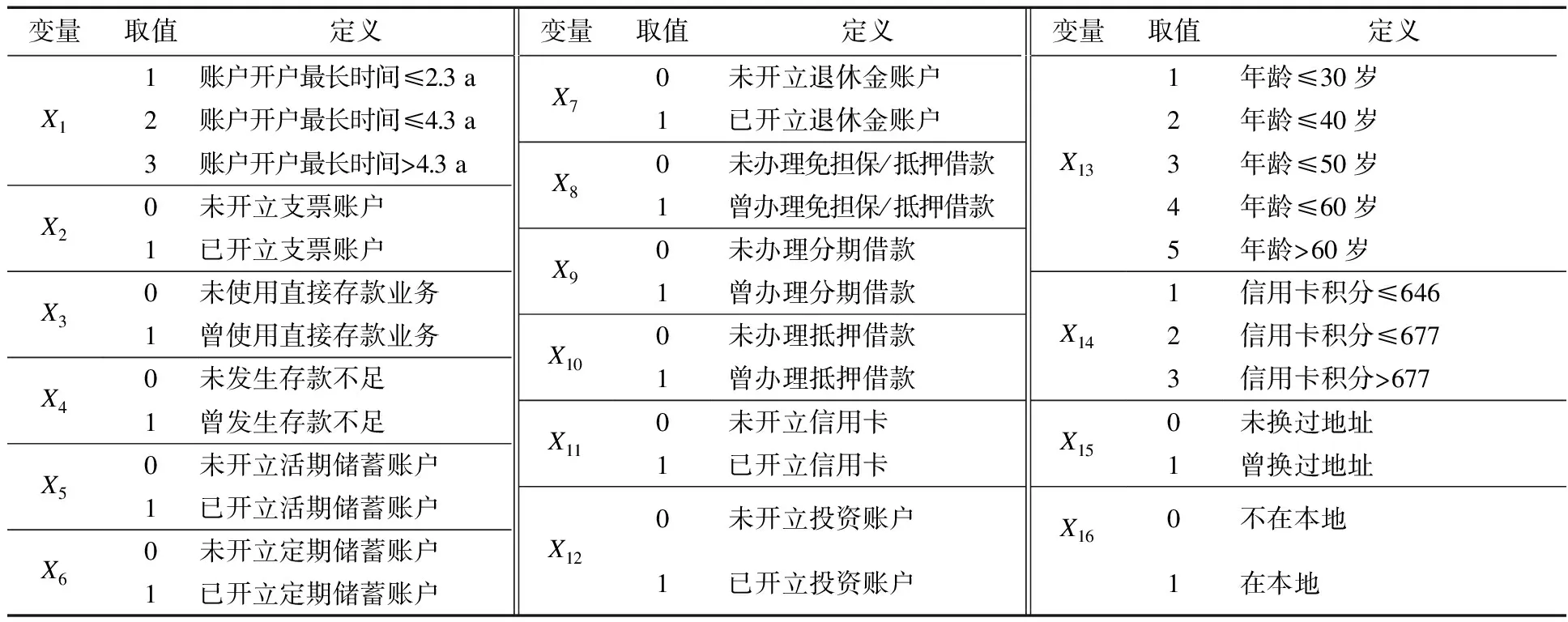
表1 16个自变量的取值和定义

表2 训练样本数据统计结果

1.2 样本数据诊断

判断样本数据是否符合Logistic回归分析的基本条件,主要考虑样本规模和样本结构两个方面.王济川和郭志刚[8]指出,Logistic回归分析的每个参数至少需要5～10个观测案例.本文研究的影响因素(自变量)为16个,从表2可以看出各组观测案例最少为119,因此样本数据满足样本规模的条件.下面将通过对过离散、空单元、多元共线性等方面进行诊断,判断样本数据是否存在数据结构的问题.

(1) 过离散 本文采用Pearson卡方检验所得的卡方值除以相应的自由度来估计离散参数,并使用SPSS中的NOMREG程序来进行计算,结果如下:卡方值为3 494.631;自由度为3 225;P值为0.001;离散参数为1.084.可以看出,离散参数近似等于1.0,这说明样本数据过离散可以忽略不计.

(2) 空单元 从表2可以看出,样本数据不存在空单元问题.

(3) 多元共线性 可根据容忍度指标来判断,当容忍度指标为零时,说明相应自变量与其他自变量完全相关;容忍度小于0.2,可以认为是多元共线性存在的标志;容忍度小于0.1,说明多元共线性很严重[8].样本数据多元共线性问题诊断结果如表3所示.表3中所有自变量的容忍度都远大于0.2,这表明不存在多元共线性问题.

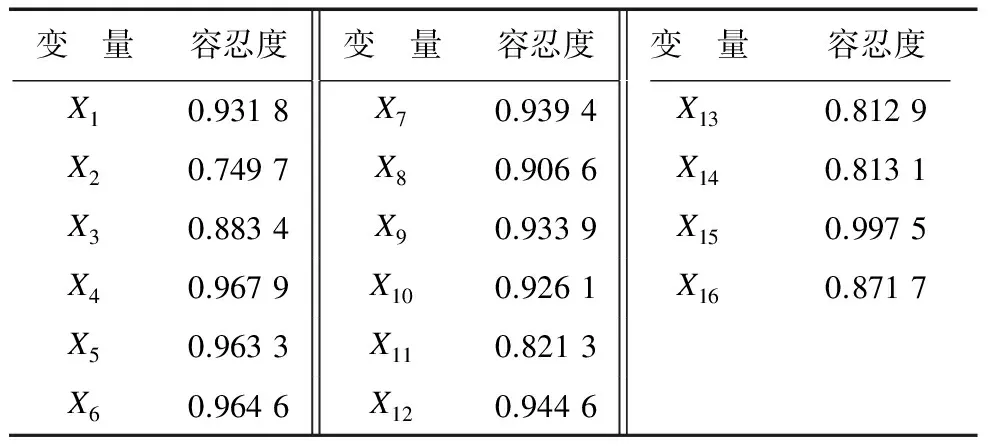
表3 样本数据多元共线性问题诊断结果

以上诊断结果说明,抽取的样本数据符合Logistic回归分析的基本条件.

2 基于Logistic回归分析的预测模型

2.1 Logistic回归分析及建模

设P为客户购买保险的概率,0≤P≤1,则1-P为没有购买保险的概率.假设Logistic回归模型为:

式中:β0——常数项;βi——回归系数,i=1,2,3,…,16.

本文运用基于最大似然估计的向前逐步回归法进行分析,基于Score检验统计量选入自变量,基于最大偏似然估计的似然比检验结果来剔除变量,分析软件选用SPSS.由于存在多分类的自变量,需要将多分类变量转换为多个哑变量,每个哑变量只代表某两个级别之间的差异,这样回归结果才能有明确而合理的实际意义.各自变量的哑变量编码如表4所示.

表4 哑变量编码

经过程序计算,在迭代12次后,模型中各变量的相应参数的检验结果如表5所示.

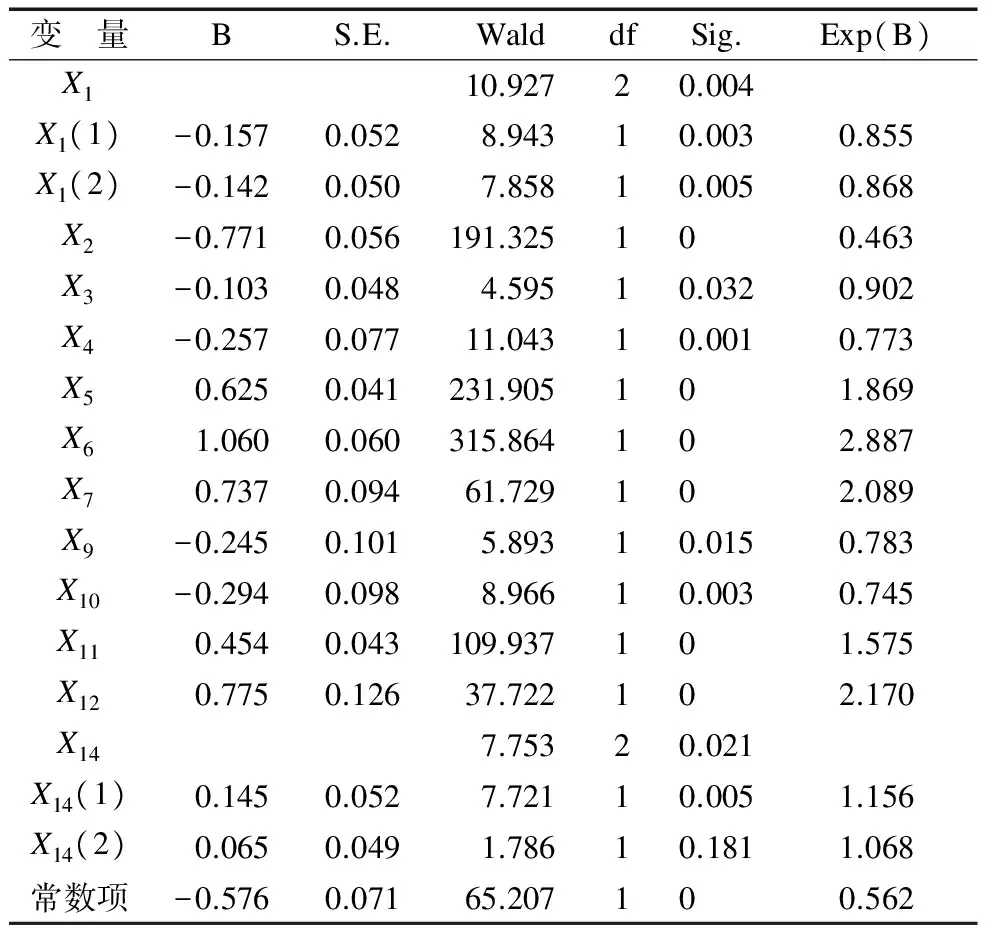
表5 模型的变量及其相应参数的检验结果

根据表5的检验结果可知,变量X8,X13,X15,X16不具有统计学意义.变量X1,X2,X3,X4,X5,X6,X7,X9,X10,X11,X12,X14具有统计学意义.因此,预测模型可以表示为:

其中:

Y=-0.576-0.157X1(1)-0.142X1(2)-

0.771X2-0.103X3-0.257X4+

0.625X5+1.060X6+0.737X7-

0.245X9-0.294X10+0.454X11+

0.775X12+0.145X14(1)+0.065X14(2)

2.2 模型拟合程度

2.2.1 特异值与特殊影响案例

本文采用Pearson残差来判断样本数据是否为特异值,如图1所示.采用杠杆度来判断样本数据是否属于特殊影响案例,如图2所示.由图1可以看出,存在Pearson残差值大于2的样本数据,这说明样本数据中存在特异值.由图2可知,样本数据的杠杆度平均值为(14+1)/12 000=0.001 25,大于2×0.001 25=0.002 5 的观测值(即杠杆点),因此样本数据中可能存在特殊影响案例.

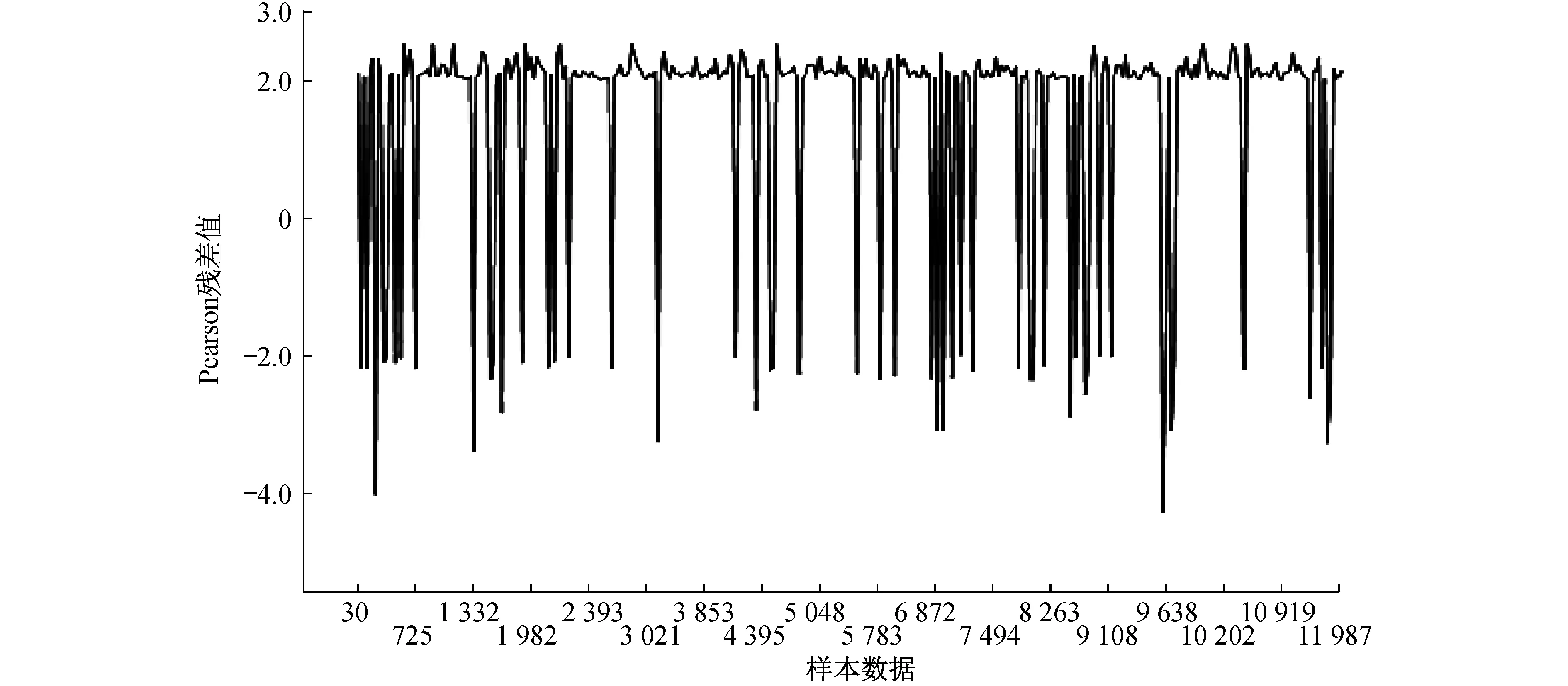
图1 训练样本数据的Pearson残差值

图2 训练样本数据的杠杆度值

为进一步判断特异值是否为特殊影响案例,将特异值的序号及对应的检验指标都查找出来,以便更清晰地观察检验结果.其中,样本数据中共有342个特异值,但杠杆度值小于0.002 5的共15个(详见表6),其Cook距离都小于最大值0.027 9,并且根据其各项dfbeta值可以看出,它们对系数估计的影响不太大,因此它们都不应算作特殊影响案例.

表6 样本数据特异值的各项检验指标值

注:DFB0_1,DFB1_1,DFB2_1,DFB3_1,DFB4_1,DFB5_1,DFB6_1,DFB7_1,DFB8_1,DFB9_1,DFB10_1,DFB11_1,DFB12_1,DFB13_1,DFB14_1—删去该案例后对各项系数估计的影响系数.

2.2.2 拟合优度检验与模型预测效果判断

本文采用Hosmer和Lemeshow检验来判断模型的拟合优度,得出结果:卡方值为15.001;自由度为8;P值为0.059,大于0.05,这表明模型预测概率获得的期望频数与观测频数之间的差异无统计意义,即模型拟合程度较好.

2.3 模型预测效果

对保留样本的5 000条数据进行预测准确率判断,结果见表7.

其中,模型对样本数据分类情况的综合预测准确率为68.3%,预测结果较好.

表7 保留样本数据预测分类情况

注:判断值为0.400.

3 影响因素分析

3.1 年龄因素

本文考虑客户年龄与客户账户年龄(账户开户最长时间)两个年龄因素.数据分析结果表明,客户年龄因素不具有统计学意义,账户年龄因素具有统计学意义.桂林[6]的研究认为,年龄因素对客户保险购买行为有一定影响.但在本文的研究中,客户年龄因素对于所研究的保险产品却不具有统计学意义,此结论是否适用于其他保险产品,有待进一步研究.

客户账户年龄因素的两个哑变量的回归系数分别为-0.157和-0.142.从回归系数可以判断,账户年龄小于2.3年的客户比大于2.3年的客户购买保险的概率高.此结论表明,新客户比老客户更倾向于购买所研究的保险产品,但该结论是否适用于其他保险产品,有待进一步研究.

3.2 账户或业务因素

本文考虑的账户或业务因素有:支票账户、直接存款业务、活期储蓄账户、定期储蓄帐户、退休金账户、信用卡业务、投资业务.这些因素的回归系数分别为-0.771,-0.103,0.625,1.060,0.737,0.454,0.775.数据表明,这7个因素都具有统计学意义.可以看出,办理活期存款账户、定期存款账户、退休金账户、信用卡业务、投资业务的客户购买所研究保险产品的概率比未办理的客户要高.而未办理支票账户、直接存款业务的客户购买所研究保险产品的概率比已办理的客户要高.

3.3 负债因素

本文考虑的负债因素有:存款不足、免担保或抵押借款、分期借款、抵押借款.研究表明,免担保或抵押贷款对所研究保险产品的购买行为不具有统计学意义,而存款不足、分期借款、抵押借款因素具有统计学意义,这3个因素的回归系数分别为-0.257,-0.245,-0.294.可以看出,未发生存款不足、未办理分期借款或抵押借款的客户购买所研究保险产品的概率比已发生或已办理的客户要高.

3.4 信用卡积分因素

数据表明,信用卡积分因素具有统计学意义,两个哑变量的回归系数分别为0.145与0.065.可以发现,积分>646的客户购买所研究保险产品的概率比积分≤646的客户要高.此结论表明,与积分低的客户相比,信用卡积分高的客户更倾向于购买所研究的保险产品,但该结论是否适用于其他保险产品,有待进一步研究.

3.5 住址因素

本文考虑的住址因素有:是否搬家、是否在本地.研究表明,这两个因素对所研究的保险产品购买行为不具有统计学意义.

4 结 语

本文基于一个零售银行客户消费数据库中的消费数据,运用Logistic回归分析方法分析了5类16个影响因素,构建了客户购买保险概率的预测模型.所涉及的影响因素范围较大,构建的模型拟合程度与预测效果较好,可以为保险企业进行客户细分和产品细分、研发满足不同客户需求的产品或服务、开展应用于不同客户的主题体验设计等方面提供科学参考.

[1] KARL Borch.The three markets for private insurance[J].The Geneva Papers on Risk and Insurane,1981(20):7-31.

[2] KUUSELA H,SPENCE M T.How consumer select life insurance policies:a protocol analysis[J].Journal of Professional Services Marketing,1998,18(1):49-63.

[3] 万晴瑶.人口、家庭结构变化对寿险消费需求的影响初探[J].上海保险,1999(11):15-17.

[4] 张洪涛,苗力.银行保险[M].北京:中国人民大学出版社,2005:1-100.

[5] 黄金财.中国银行保险发展的模式选择[J].保险研究,2006(11):39-40.

[6] 桂林.银行保险消费行为研究——以重庆寿险的银行保险为例[D].重庆:西南大学,2012.

[7] 中国工商银行上海市分行课题组.商业银行财富客户金融消费行为的统计与分析[J].金融论坛,2011(3):58-63.

[8] 王济川,郭志刚.Logistic回归模型——方法与应用[M].北京:高等教育出版社,2001:57-218.

[9] 于洪霞,季建华,李兴.一种基于Logistic回归的全损飞行事故分析与预测[J].中国安全科学学报,2010,20(3):34-38.

[10] MIKE Patetta.Predictive modeling using logistic regression[M].Cary:SAS Institute Inc,2008:1-15.

(编辑 白林雪)

Analysis and Forecast Model of Bancassurance Consuming Behavior Based on Logistic Regression Method

YU Hongxia1, LI Xing2

(1.SchoolofMathematicsandPhysics,ShanghaiUniversityofElectricPower,Shanghai201300,China; 2.UnderwritingDept.ofConsumerLine,HuataiP&CInsuranceCo.Ltd,Shanghai201315,China)

Logistic regression method is applied to analyze effect factors of bancassurance consuming behavior and build a forecast model.Then the model is tested with reserved sample.Through the diagnosis of overdispersion,zero cell count,multicollinearity,outliers,influential observations and test of level of fitness and predictive accuracy,the model is proved to be adequate and effective,indicating that 12 factors are of significance in statistics science.

bancassurance; consuming behavior analysis; categorical variables; logistic regression method

10.3969/j.issn.1006-4729.2017.03.019

2015-09-09

于洪霞(1978-),女,博士,讲师,辽宁朝阳人.主要研究方向为最优化理论及应用.E-mail:yuhongxialx@aliyun.com.

O212;F842.6

A

1006-4729(2017)03-0307-06