Ag-MgF2弥散结构复合薄膜的光学吸收特性

董睿曦, 朱群志

(上海电力学院 能源与机械工程学院, 上海 200090)



Ag-MgF2弥散结构复合薄膜的光学吸收特性

董睿曦, 朱群志

(上海电力学院 能源与机械工程学院, 上海 200090)

金属纳米颗粒和电介质基体构成弥散结构复合薄膜,由于局域表面发生等离子体共振效应,复合薄膜在一定光谱范围内会出现吸收峰增强的现象,而金属颗粒体积分数是影响共振吸收峰位置和强度的关键因素.分别采用有效介质理论和时域有限差分法对复合薄膜的吸收特性进行计算,讨论改变掺混颗粒体积分数对薄膜吸收率的影响.研究得出,随着体积分数的增加,更易在可见光波段产生强吸收峰.这一研究结果有助于掌握弥散结构复合薄膜吸收特性的影响机理.

复合薄膜; 等离子体共振; 有效介质理论; 时域有限差分法

由于石油、煤炭等化石资源的日益枯竭以及碳排放引起的全球气候变暖,太阳能等绿色能源的研究和运用越来越受到世界各国的重视.国内外有许多的前沿研究工作,将金属纳米颗粒与太阳能光伏电池结合,以提高太阳能的转换效率[1-6].WOKAUN A研究发现,通过改变金属颗粒的尺寸和形状、基体材料,或者改变金属颗粒在基体中的体积分数,都可以控制金属粒子表面等离子体共振的频率和强度,满足光电材料的要求[7].

将金属颗粒分布在陶瓷基体材料中可形成弥散结构复合薄膜,由于金属颗粒的局域表面发生等离子体共振效应,弥散结构复合薄膜在一定光谱范围内,其吸收峰将得到增强.这类复合薄膜材料具有特殊的吸收特性,在太阳能采集和转换器件方面具有应用前景,引起了研究人员的广泛兴趣[8].Ag-MgF2弥散结构复合薄膜拥有特异的光学和电学性质,是一种有前景的功能性材料[9].目前,金属-陶瓷弥散结构复合薄膜在实际工程中的应用较少,一个重要原因是对陶瓷材料和金属颗粒构成的弥散结构复合薄膜研究尚不完善,薄膜结构参数对薄膜性能的影响机理有待进一步研究.大多数文献采用有效介质理论来计算弥散结构薄膜的光学常数(n,k),然后得出弥散薄膜的透反射率.由于有效介质理论有一定的使用条件,得出的结论具有一定局限性.本文采用时域有限差分法对陶瓷材料氟化镁和金属银颗粒构成的弥散结构复合薄膜的吸收特性进行研究,并与有效介质理论得出的结果相比较,分析体积分数对复合薄膜光学吸收特性的影响.

1 研究模型与理论预测

1.1 薄膜结构及参数

本文研究的弥散结构复合薄膜是由陶瓷基体和金属银颗粒组成,结构如图1所示.银颗粒的尺寸为纳米级;基体材料为MgF2.银颗粒随机分散在MgF2基体中,形成弥散结构复合薄膜.

图1 金属银颗粒弥散于基体中形成的复合薄膜

1.2 球形粒子等离子体共振效应

当入射光照射复合薄膜时,球形金属纳米颗粒表面的自由电子由于极化作用产生偶极子,电场方向改变时,产生相反方向的偶极子,如此反复形成电子振动.这些偶极子随着电磁场的变化而集体振荡,使得金属颗粒表面的电磁场增强,有利于对入射光子的捕捉,从而使特定波长下的吸收率有所增加.

金属颗粒掺混于陶瓷基体中形成弥散结构复合薄膜,该弥散结构薄膜吸收系数可以应用Mie理论的偶极子近似(准静态近似)来描述[10]:

(1)

式中:α——吸收系数;λ——波长;f——金属颗粒体积分数;ω——角频率;εm——基体介电常数;ε1(ω)——金属颗粒介电常数实部;ε2(ω)——金属颗粒介电常数虚部.

对于MgF2等非吸收绝缘基体,其介电常数虚部非常小,所以按近似为零处理,并且其介电常数实部基本不随波长发生变化,可视为常数.由式(1)可知,若吸收系数α取最大值,则需满足以下条件[11]:

(2)

此时,所对应的波长即为等离子体共振的波长.图2给出了Ag-MgF2弥散结构复合薄膜ε1(ω)+2εm与λ的关系曲线,其中光学常数取自文献[12].

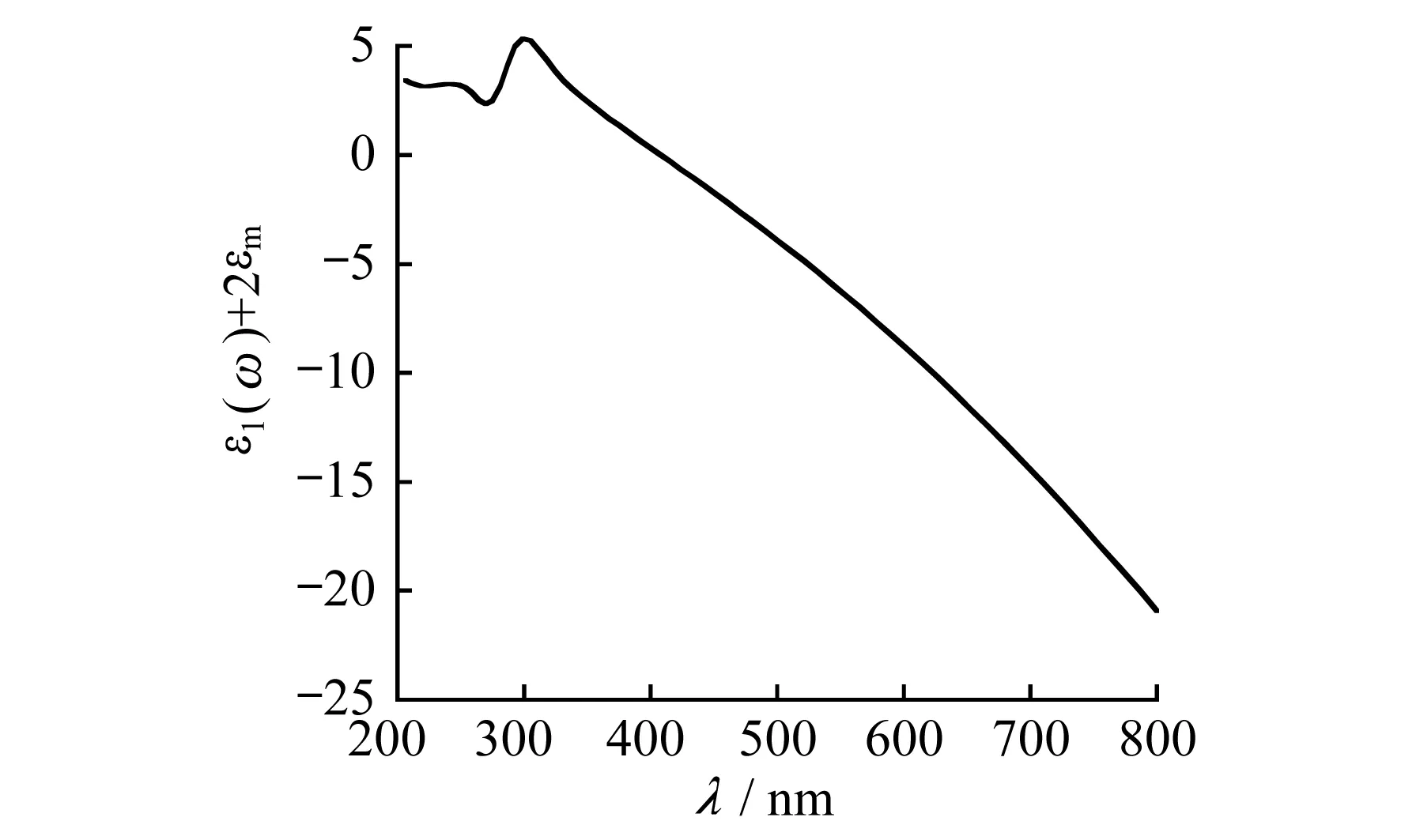
图2 ε1(ω)+2εm与λ的关系曲线

由图2可以看出,波长为400 nm时满足式(2).由此可以推测,Ag-MgF2弥散结构复合薄膜的共振波长位置在400 nm附近.

1.3 有效介质理论

对于微纳尺度金属颗粒与非金属基质形成的复合物,其光学和介电特性与微细结构有密切关联,有效介质理论是基于非均匀复合介质各组分的介电函数近似给出复合介质的等效介电函数.

1.3.1 Maxwell-Garnett理论

假设介电常数为εp的金属颗粒弥散于介电常数为εm的陶瓷基体中,则Maxwell-Garnett(以下简称“M-G”)关系式为[13]:

(3)

式中:ε——复合物有效介电常数;εp——金属颗粒介电常数.

根据式(3)可以得出复合物有效介电常数为:

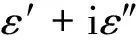
(4)

式中:ε′——复合薄膜介电常数实部;ε″——复合薄膜介电常数虚部.

在光频范围内,由Maxwell关系式可知,复合薄膜的光学复折射率N与有效介电常数之间的关系为:

(5)

式中:n——复合薄膜光学折射率;k——复合薄膜消光系数.

根据式(4)和式(5)可以得出:

(6)

(7)

最后,利用透射系数ρ和反射系数τ得出吸收率A,ρ和τ的计算式见文献[14].

(8)

1.3.2 Bruggeman理论

在考虑粒子间相互作用的情况下,BRUGGEMAN采用平均场理论导出了复合薄膜有效介电常数的Bruggeman(以下简称“B-G”)关系式[15]:

(9)

由式(9)可整理出复合薄膜的介电常数为[15]:

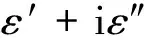
(10)

之后分离出复合薄膜介电常数的实部和虚部,根据式(6)和式(7)得到折射率和消光系数,最终得到吸收率.

2 仿真计算

2.1 时域有限差分法

时域有限差分法是由YEE K S提出的求解电磁场麦克斯韦方程的方法.其核心思想是将带时间变量的Maxwell旋度方程转化为差分形式,模拟出电子脉冲和理想导体作用的时域响应[16].该方法的优点是能够直接模拟电磁场的分布,且精度较高.

材料的介电常数是入射光频率的函数,取决于物质内部电荷在外部电磁场的作用下引起的极化电场的强弱.Lorentz-Drude 模型是一种常用的介电常数模型,它将材料的复介电常数表示为自由电子的带内效应与束缚电子的带间效应作用之和[17].

(11)

式中:ε(ω)——材料的复介电常数;ε∞——频率无穷大时的相对介电常数;ωm——第m个谐振子的共振频率;ωmp——第m个谐振子的等离子体频率;γm——第m个谐振子的阻尼系数.

将计算得出的粒子周围近场信息进行远场外推,就可以获得物体的远场散射或吸收信息,从而可以得到材料的吸收率.

2.2 建模及模拟过程

本文采用时域有限差分法模拟银颗粒随机分布在陶瓷基体中,得出紫外及可见光区间的光谱吸收率.计算中采用的复合薄膜厚度为100 nm,银颗粒选用3种半径分别为5 nm,7.5 nm,10 nm.银颗粒随机分布在陶瓷基体中,颗粒个数由金属的体积分数确定.考虑到仿真收敛性与计算时间等因素,仿真区域设置为X=Y=150 nm,Z=1 500 nm;网格大小设为1 nm×1 nm×1 nm;X方向和Y方向(垂直于光线传播方向)设置为周期边界条件,Z方向(沿光线传播方向)设置为完美匹配层边界条件.入射光为200～800 nm平面波光源,沿Z正方向射入.通过频域功率监视器可获得弥散薄膜的反射率和透射率,然后根据能量守恒计算出薄膜的吸收率.

由于颗粒为随机分布,为了获得统计平均值,在其他参数不变的情况下,对20个随机得到的弥散薄膜结构分别进行了计算,然后对20组数据进行算术平均.

3 结果与讨论

3.1 有效介质理论预测结果

根据M-G关系式分别计算了体积分数为1%,5%,10%,15%,20%的Ag-MgF2弥散结构复合薄膜,在200～800 nm波长范围内,得出吸收率随波长的变化曲线如图3所示.计算中的数据取自文献 [12].

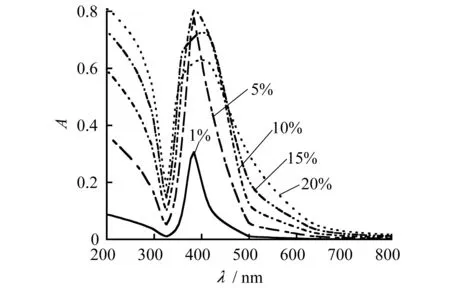
图3 M-G理论计算不同体积分数下Ag-MgF2弥散结构薄膜的吸收率

由图3可知,在紫外波段,随着波长的增加,5条吸收率曲线均出现下降,至325 nm时出现极小值;之后所有吸收率曲线随波长的增加而迅速升高,于380～390 nm时出现最大值,吸收峰对应的波长小于由Mie得到的共振波长;之后所有曲线均缓慢下降.此外,弥散结构薄膜吸收率曲线的峰值随着银颗粒体积分数的增大而升高,峰位略微红移.其中,体积分数为1%时,吸收峰位于380 nm处,峰值为0.30;体积分数为5%时,吸收峰位于381 nm处,峰值为0.78;体积分数为10%时,吸收峰位于385 nm处,峰值为0.80;体积分数为15%时,吸收峰位于390 nm处,峰值为0.72;体积分数为20%时,吸收峰位于395 nm处,峰值为0.62.

根据B-G关系式计算了体积分数为1%,5%,10%,15%,20%的Ag-MgF2弥散结构复合薄膜,在200～800 nm波长范围内,得出吸收率随波长变化的曲线如图4所示,计算中的数据取自文献[12].

由图4可以看出,在紫外波段,随着波长的增加,所有曲线均出现吸收率下降,至325 nm附近出现极小值;之后所有吸收率曲线随着波长的增加而升高,于390～400 nm处出现吸收峰,吸收峰对应波长略小于由Mie得到的共振波长,且吸收峰较宽;之后曲线均缓慢下降.其中,体积分数为1%时,吸收峰位于390 nm处,峰值为0.18;体积分数为5%时,吸收峰位于392 nm处,峰值为0.54;体积分数为10%时,吸收峰位于395 nm处,峰值为0.70;体积分数为15%时,吸收峰位于397 nm处,峰值为0.76;体积分数为20%时,吸收峰位于399 nm,峰值为0.80.结合图3和图4可以发现,相同体积分数下,用B-G理论得出的曲线峰值比M-G理论得出的曲线峰值宽一些,这可能是由于B-G理论考虑了颗粒与颗粒间的相互作用.

图4 B-G理论计算不同体积分数下Ag-MgF2弥散结构薄膜的吸收率

3.2 时域有限差分法的仿真结果

根据时域有限差分法模拟计算粒径为5 nm的Ag颗粒在体积分数为1%,5%,10%,15%,20%情况下,Ag-MgF2弥散结构复合薄膜的吸收率曲线,如图5所示.

由图5可以看出,当波长在200～320 nm时,吸收率随波长的增加而减小,至320 nm附近出现极小值;随后,吸收率曲线随波长的增加而迅速升高,在360 nm附近出现最大值;而在360～800 nm波段内,吸收率随波长的增加而迅速下降.其中,体积分数为1%时,吸收峰位于356 nm处,峰值为0.16;体积分数为5%时,吸收峰位于357 nm处,峰值为0.47;体积分数为10%时,吸收峰位于359 nm处,峰值为0.63;体积分数为15%时,吸收峰位于361 nm处,峰值为0.71;体积分数为20%时,吸收峰位于362 nm,峰值为0.76.由此可见,银纳米颗粒复合薄膜的吸收峰出现在360 nm附近,与图3中预测的峰值较相近,这说明银纳米粒子产生了局域表面等离子共振.随着体积分数的增大,吸收峰位置略微红移,强度明显增大.其原因是:随着体积分数的增加,银纳米颗粒间距减小,激发的表面等离激元会通过光子隧道效应发生耦合,耦合的加剧使得吸收峰红移[11];另一方面,随着银纳米颗粒数目的增多,颗粒中被激发的等离子激元产生的电磁场加强,其发生等离子共振的机会增加,从而使得复合薄膜吸收峰上升.

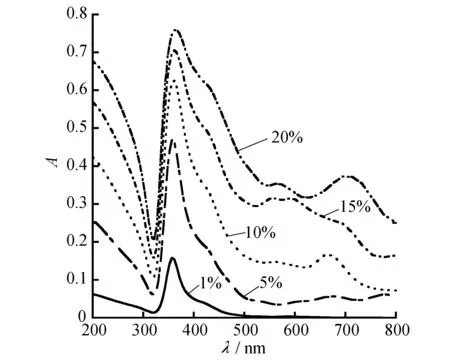
图5 半径为5 nm的Ag-MgF2复合薄膜吸收率曲线

粒径为5 nm,体积分数为20%,假设颗粒呈菱形阵列,则可以得出两粒子的间距[18],由此可以利用时域有限差分法模拟得出两银粒子间的电场分布,如图6所示.

图6 银粒子对间电场分布示意

由图6可以看出,半径为5 nm的银粒子对,两粒子球心间距为15.4 nm,在平行入射光的照射下,粒子对间产生强烈的等离子共振效应,导致银粒子对间电场强度相对于入射电场强度增加了5倍以上,由于粒子间电场强度的增强,使得复合薄膜对于入射光子的捕捉能力增强,从而导致图5中高吸收峰的形成.

3.3 3种计算结果比较

将有效介质理论Maxwell-Garnett理论和Bruggeman理论的预测值分别与时域有限差分法仿真值进行比较,结果如图7所示.

图7 3种理论仿真结果对比示意

由图7可以看出,Bruggeman理论的计算结果更加符合仿真结果.究其原因有:当体积分数在1%～20%之间时,颗粒间的相互作用已不能忽略,而Maxwell-Garnett理论适用于描述颗粒与颗粒间相互作用可以忽略的情况;Bruggeman理论用于描述颗粒间距离较小,且需要考虑颗粒间相互作用的情况,所以Bruggeman理论得到的吸收峰更加符合实际情况.但是Bruggeman理论结果与仿真结果在400 nm之后仍有一定的差距,其原因可能在于有效介质理论未考虑微尺度效应对其整体结构的影响.

4 结 论

(1) Mie理论的偶极子近似方法与有效介质理论得出的共振波长有一定差异,可知两种理论描述都有一定的局限性.

(2) 与时域有限差分法模拟计算相比,Bruggeman理论计算得出的吸收峰更加符合仿真结果.

(3) 改变颗粒的体积分数对吸收峰高度的调节有相当大的作用.体积分数每增加5%,吸收峰强度相应增加1.1～4倍.因此,可以通过调节颗粒在其中的体积分数对复合薄膜的吸收光谱特征进行调节.

[1] MENG X,DEPAUW V,GOMARD G,etal.Design,fabrication and optical characterization of photonic crystal assisted thin film monocrystalline-silicon solar cells[J].Optics Express,2012,20(S4):A465-75.

[2] OH J,YUAN H C,BRANZ H M.An 18.2%-efficient black-silicon solar cell achieved through control of carrier recombination in nanostructures[J].Nature nanotechnology,2012,7(11):743-748.

[3] GARNETT E,YANG P.Light trapping in silicon nanowire solar cells[J].Nano letters,2010,10(3):1 082-1 087.

[4] ZANOTTO S,LISCIDINI M,ANDREANI L C.Light trapping regimes in thin-film silicon solar cells with a photonic pattern[J].Opt.Express,2010,18(5):4 260-42 74.

[5] BECK F J,MOKKAPATI S,CATCHPOLE K R.Plasmonic light-trapping for Si solar cells using self-assembled,Ag nanoparticles[J].Progress in Photovoltaics:Research and Applications,2010,18(7):500-504.

[6] GRANDIDIER J,DECEGLIE M G,CALLAHAN D M,etal.Simulations of solar cell absorption enhancement using resonant modes of a nanosphere array[J].Journal of Photonics for Energy,2012,2(1):024502/1-11.

[7] WOKAUN A.Surface enhancement of optical fields[J].Molecular Physics an International Journal at the Interface Between Chemistry & Physics,1985,56(1):1-33.

[8] 史守华,孙兆奇,孙大明.Ag-MgF2复合纳米金属陶瓷薄膜的微结构及吸收光谱特性研究[J].光学学报,2002,22(5):622-626.

[9] 王磊,蔡琪,王佩红,等.Ag-MgF2复合纳米金属陶瓷薄膜的微粒尺寸效应[J].真空科学与技术学报,2003,23(5):319-322.

[10] 杨修春,刘会欣,李玲玲,等.影响贵金属纳米颗粒表面等离子体共振因素评述[J].功能材料,2010,41(2):341-345.

[11] BOHREN C F,HUFFMAN D R.Absorption and scattering of light by small paticles[M].New York:John Wiley & Sons,1998:223-237.

[12] MARVIN J Weber.Handbook of optical materials[M].Boca Raton,USA:CRC Press,2003:351-352.

[13] MAXWELL-GARNETT J C.Colours in metal glasses and metal films[J].Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences,1904,203(359-371):385-420.

[14] Zhoumin M.ZHANG.Nano/microscale heat transfer[M].New York:McGraw-Hill,2007:335.

[15] GRANQVIST C G.Photothermal conversion of solar energy by gold cermet coatings:applicability of the bruggeman effective medium theory[J].Journal of Applied Physics,1979,50(4):2 916-2 920.

[16] 葛德彪.电磁波时域有限差分方法[M].西安:西安电子科技大学出版社,2002:208-210.

[17] 谢处方,绕克谨.电磁场与电磁波[M].第4版.北京:高等教育出版社,2006:298.

[18] 谈和平,夏新林,刘林华,等.红外辐射特性与传输的数值计算——计算热幅射学[M].哈尔滨:哈尔滨工业大学出版社,2006:119.

(编辑 白林雪)

Optical Absorption Properties of Ag-MgF2Composite Film

DONG Ruixi, ZHU Qunzhi

(SchoolofEnergyandMechanicalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

Composite film by the micro and nanoscale metal particles and insulating matrix can obtain strong nonlinear physical effects.Different volume fraction will produce different localized plasmon resonance effect,resulting in different absorption peak height and position.Effective medium theory and finite difference time domain method is used to calculate the absorption rate of the composite film.The impact of changing the volume fraction on the absorption rate is discussed.The analysis shows that with increasing volume fraction it is easy to produce high-intensity absorption peak in the visible band.The results help to grasp the mechanism of absorption characteristics of the composite film.

composite film; plasmon resonance; effective medium theory; finite difference time domain method

10.3969/j.issn.1006-4729.2017.03.013

2016-04-29

朱群志(1972-),男,博士,教授,浙江台州人.主要研究方向为材料热辐射物性,辐射换热,太阳能利用.E-mail:zhuqunzhi@shiep.edu.cn.

国家自然科学基金(51576119).

O484.41

A

1006-4729(2017)03-0279-06