新型小波阈值函数的仿真及应用

范海哲, 王 昊, 韩春辉

(上海电力学院 能源与机械工程学院, 上海 200090)



新型小波阈值函数的仿真及应用

范海哲, 王 昊, 韩春辉

(上海电力学院 能源与机械工程学院, 上海 200090)

提出了一种新型小波阈值函数.借助于典型信号和高斯白噪声叠加形成测试信号,对传统小波阈值函数、改进小波阈值函数及新型小波阈值函数的去噪效果进行对比仿真研究.结果表明,采用新型小波阈值函数所得到的去噪信号,其信噪比和均方差均最优.此外,将新型小波阈值函数用于滚动轴承的实际振动信号的去噪研究,从去噪信号的时域信号对比及信噪比来看,该函数具有较好的去噪效果,使信噪比得到了较大提高.

小波阈值函数; 小波分析; 振动信号; 信噪比; 滚动轴承

在机械环境中,系统内部和外部环境的影响,使测得的信号往往存在噪声,而由于噪声的干扰,会导致一些错误的判断.因此,信号的去噪技术已成为各领域的热门话题,对于去噪方法的研究很有必要.由于具有低熵性、多分辨率、去相关性等特点,小波变换成为信号去噪的常用技术,并应用于诸多领域.在损伤检测中,小波包与声发射技术相结合组成的一种在线损伤检测方法,能够准确地实现对不同损伤状态的识别[1].在图像处理中,通过小波分析将不同条件下形成的图像信息进行整合从而更利于识别[2].在故障诊断中,对信号进行小波分析,根据能量分布选择时频区域,成功分离特征向量,从而完成诊断[3]等.

此外,还提出了很多以小波理论为基础的方法.例如:小波变换模极大值法,对小波系数的模极大值进行处理,去除噪声的模极大值[4];小波系数相关性法,将两个相邻层上的高频小波系数直接相乘,使信号增强,从而抑制噪声[5];小波阈值法,通过小波分解以及选择合适的阈值,使大部分噪声的小波系数置零,尽可能地保留有用信号,再通过小波系数的重构得到去噪后的信号[6].小波阈值法具有对原始信号的最优估计性、广泛适用性等优点,因此在小波去噪研究中应用最为广泛,也引起了很大的关注.但是基本的软硬阈值方法依然需要改进[7],如硬阈值函数可能造成振荡,软阈值函数容易造成高频信息的丢失,这些都对去噪效果产生了影响.为了对上述问题进行改进,国内外学者提出了相应的改进方法[8-9],如折中阈值函数、指数阈值函数、对数阈值函数等,但去噪效果都不是很理想.

本文以小波阈值函数去噪为目的,针对传统阈值函数及现有改进阈值函数的不足,总结了阈值函数进一步改进的条件,并提出了新型的小波阈值函数.对几种小波阈值函数的去噪效果进行了仿真研究,并将新型小波阈值函数应用到滚动轴承振动信号的去噪过程中,以证明其有效性.

1 传统小波阈值函数

1.1 小波阈值去噪

小波阈值去噪最基本的目的是使原始信号和噪声实现最大程度的分离。首先,设定阈值;然后,对高频小波系数进行阈值处理,对低频小波系数和阈值处理后的高频小波系数进行重构;最后,得到去噪后的信号.

1.2 小波分解层数的确定原则

小波分解层数的确定原则是:当相邻两层高频系数的标准差相差在一个可允许范围内时,则分解停止.因为在较高的分解层中,原始信号(不含噪声)在小波系数中所占的比例较大.也就是说,随着分解层数的增加,噪声信号在小波系数中所占的比例会逐渐减小,其标准差就会变大.

1.3 传统阈值函数

软硬阈值方法是最传统的小波系数处理方法,两者的表达式分别为:

(1)

(2)

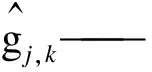
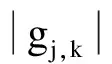
对于函数的平滑性,将gj,k=λ处连续的阈值函数称为平滑阈值函数,则该函数具有平滑性.函数的自然过渡性是指不仅连续,而且在噪声与自然信号之间存在一个平滑的过渡区,符合信号连续的特点,可以减少震荡和不必要噪声的引入.

2 改进的小波阈值函数

针对软硬阈值方法的缺陷,国内外学者提出了相应的阈值函数改进方法.本文选择了3种比较有代表性的阈值函数方法进行对比性研究,并通过观察总结提出了一种新型的小波阈值函数方法.

2.1 软硬阈值折中函数

软硬阈值折中函数的表达式为[10]:

(3)

式中:α——可变参数,α∈[0,1].

当gj,k∈[-1,1],α=λ=0.5时,软硬阈值折中函数如图1所示.

当α=0时,该阈值函数与硬阈值函数等效;当α=1时,该阈值函数与软阈值函数等效.α值的改变可以使函数在软、硬阈值函数之间灵活调整,并可以克服软阈值函数中存在恒定偏差的缺点,但该函数只是对软硬阈值进行折中,并无平滑作用.

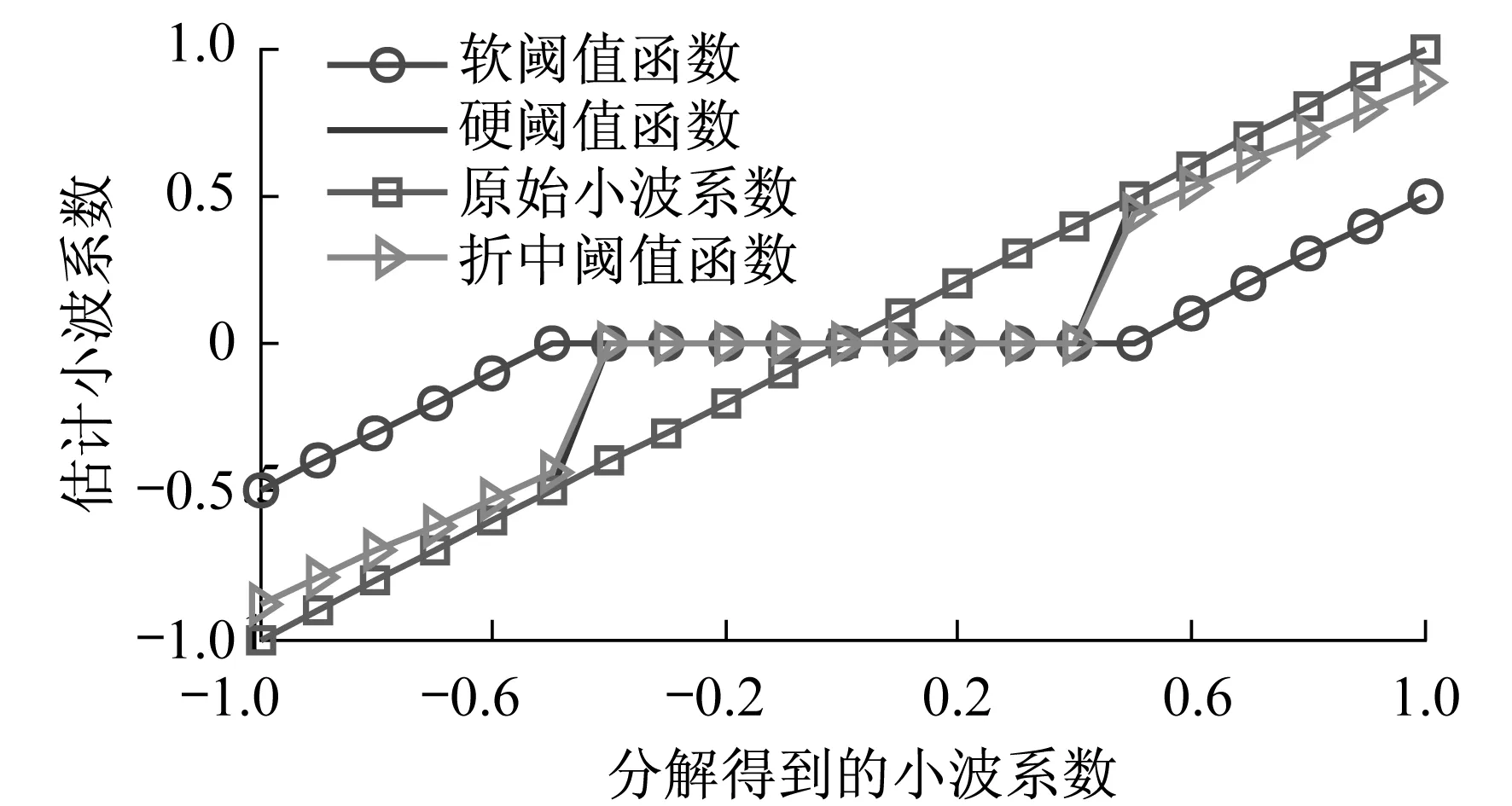
图1 软硬阈值折中函数

2.2 指数阈值函数

指数阈值函数表达式为[11]:

(4)

式中:n——任意正整数.

当gj,k∈[-1,1],n=λ=0.5时,指数阈值函数如图2所示.

图2 指数阈值函数

2.3 对数阈值函数

对数阈值函数表达式为[12]:

(5)

式中:t——调节因子,0≤t≤1,取黄金分割t=0.618;

n——正整数.

当gj,k∈[-1,1],t=0.618,n=λ=0.5时,对数阈值函数如图3所示.

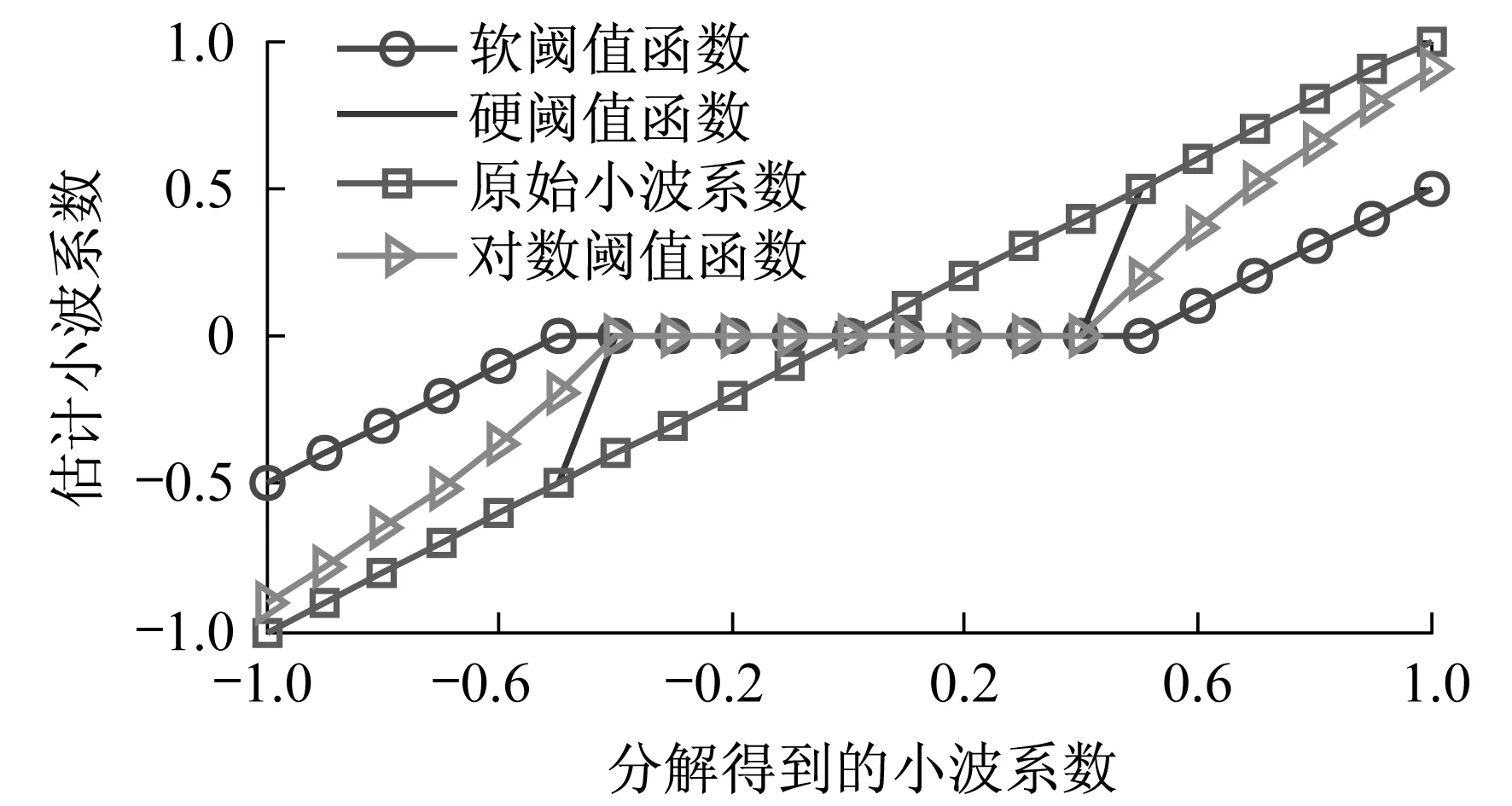
图3 对数阈值函数

3 新型小波阈值函数

通过对传统小波阈值函数及改进小波阈值函数的对比分析,可以得到进一步改进小波阈值函数的条件.

考虑到传统小波阈值函数及改进小波阈值函数在平滑性和自然过渡性方面的不足,根据上述条件,构造出新型小波阈值函数的表达式为:

(6)

式中:n,m,K——可变参数.

当gj,k∈[-1,1],n=λ=0.5时,m=1,K=2/3,新型小波阈值函数如图4所示.

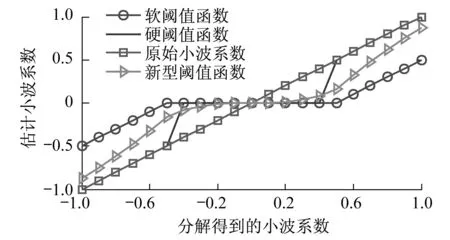
图4 新型小波阈值函数

该新型小波阈值函数具有如下特点.

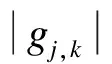
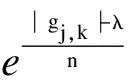
(3) 减少了高频有用信息的损失,在噪声与自然信号之间通过一个自然过渡区,符合信号的连续特征,可以减少震荡和不必要噪声的引入.

上述阈值函数的特性如表1所示.

表1 不同阈值函数的特性

4 仿真实验及性能对比研究

4.1 仿真条件

本文采用Blocks(块)和Bumps(颠簸)两种具有典型特征的信号[13],添加相同信噪比的高斯白噪声作为仿真测试信号.通过仿真实验,小波基选择效果最好的sym8小波,根据前文叙述的分层方法将其进行4层分解,并采用启发式阈值选择规则.

4.2 去噪效果评价标准

为了测试小波阈值函数的去噪效果,目前常用的方法是计算去噪信号的信噪比RSN和均方差EMS.信噪比越大,均方差越小,则说明去噪效果越好.RSN与EMS的函数表达式为:

(7)

(8)

式中:f——原始信号; s——去噪后的信号; N——信号长度.

4.3 仿真结果比较

图5与图6分别是Blocks信号和Bumps信号的原始信号、添加噪声之后的信号以及通过新型小波阈值函数去噪后的信号.

图5 Blocks信号去噪效果比较

为针对两种仿真测试信号,使用几种小波阈值函数进行去噪后,去噪信号的信噪比和均方差如表2所示.

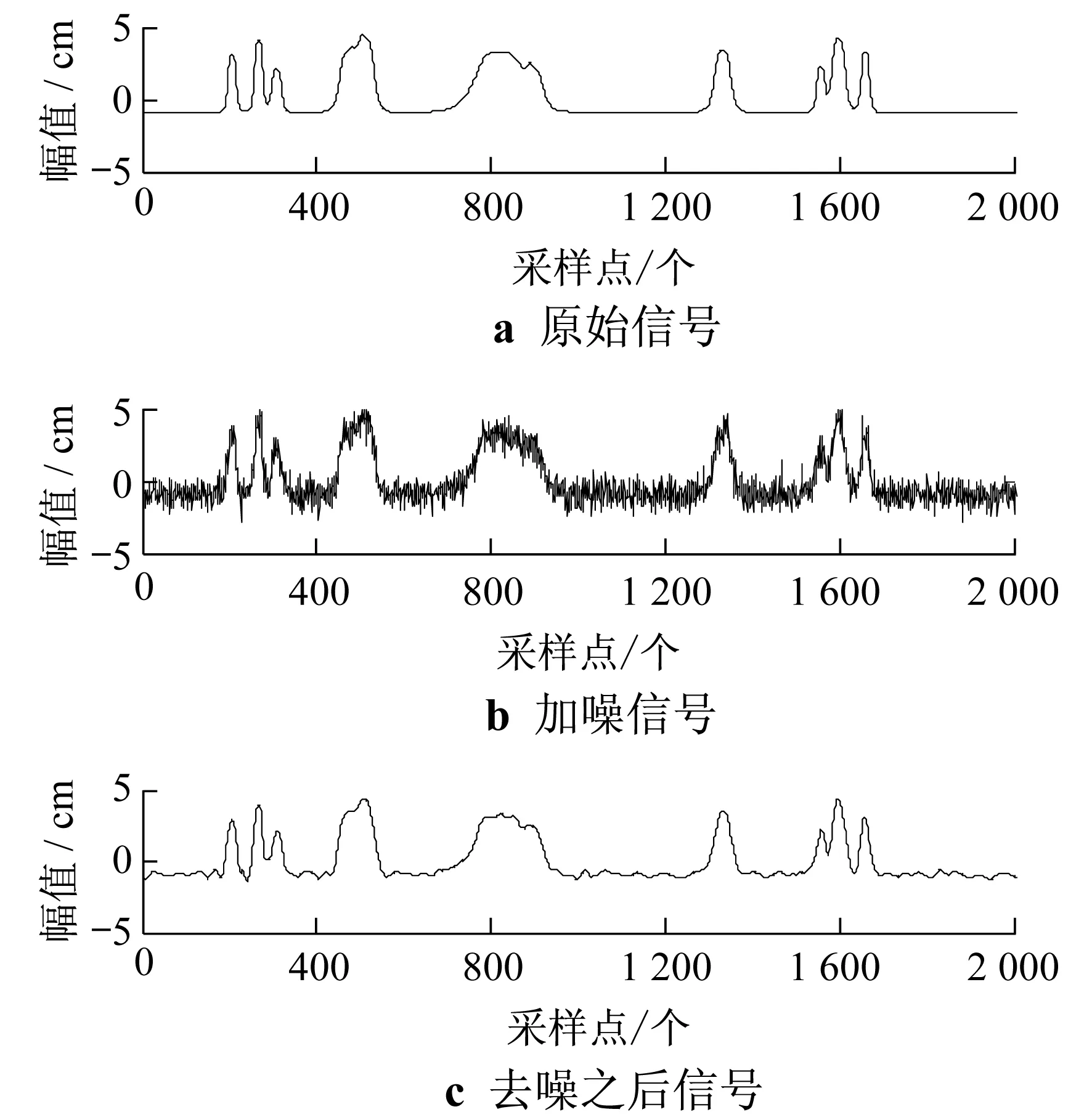
图6 Bumps信号去噪效果比较

函 数BlocksRSNEMSBumpsRSNEMS硬阈值14．77900．130617．16700．0455软阈值13．75110．165516．85560．0489折中14．11830．152016．99260．0474对数14．44040．141216．85800．0488指数14．68900．133316．07420．0585新型阈值15．16140．009617．65910．0406

根据表2可以得到如下结论:新型阈值函数对于两种不同的测试信号都非常有效,信噪比最大、均方差最小,均优于其他各种阈值函数,这与该新型阈值函数的平滑性和自然过渡性有关;对于其他几种阈值函数,针对不同的仿真测试信号,有不同的去噪效果,无论是信噪比还是均方差,没有明显的去噪优势.

5 滚动轴承实验

为了验证新型小波阈值函数的去噪效果,将其用于滚动轴承实验信号的去噪.数据采集于旋转机械故障诊断试验台,实验台由三相交流变频电机(功率为0.55 kW)、机械传动装置、传感器、计算机以及配套的软件组成,如图7所示.滚动轴承的型号为N205.

图7 旋转机械故障诊断试验台

测得真实的滚动轴承外圈故障振动信号,应用前文提到的各种小波阈值函数对其进行去噪.其中,应用新型小波阈值函数去噪前后的时域曲线图如图8所示.各种小波阈值函数去噪后的信噪比和均方差如表3所示.

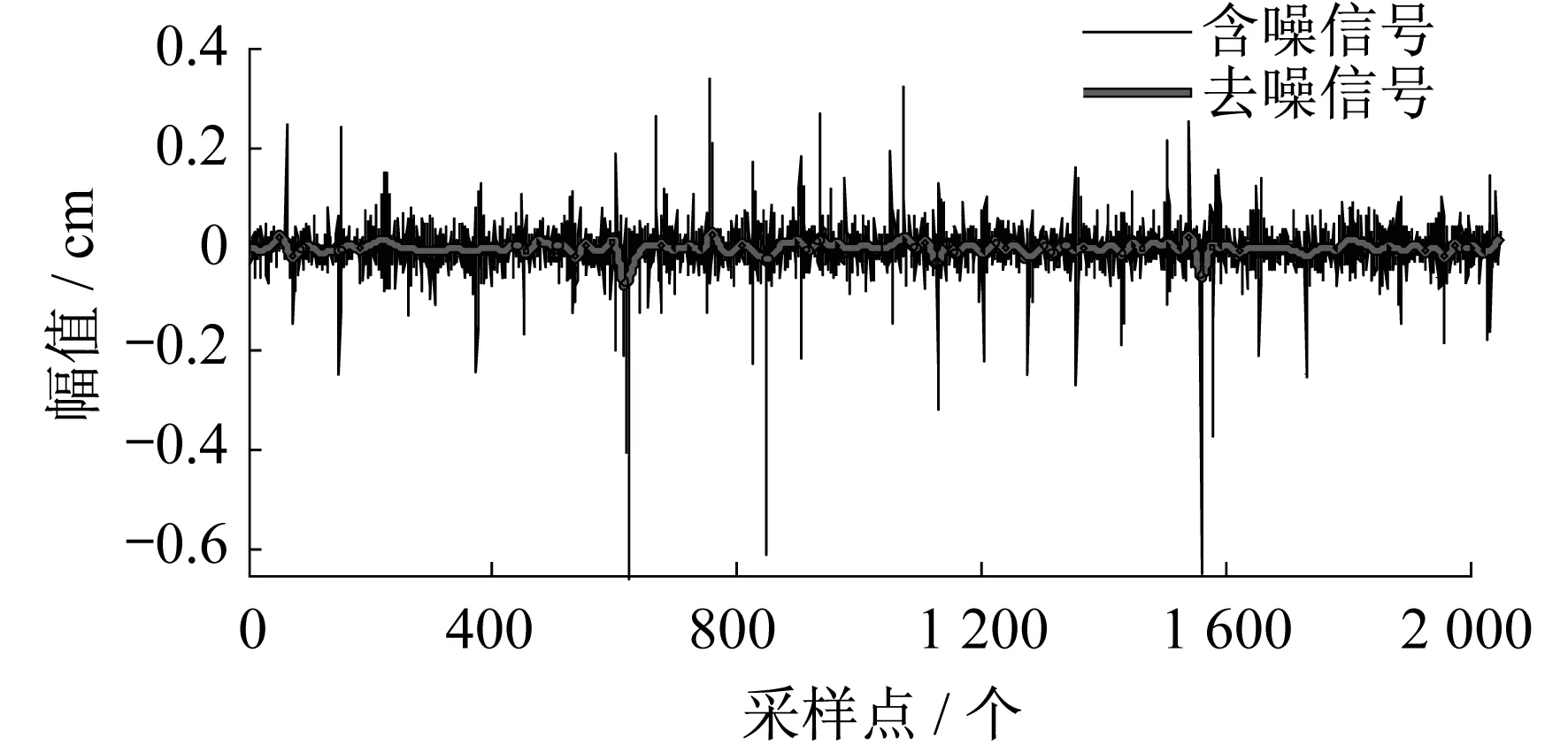
图8 滚动轴承外圈故障振动信号去噪前后时域曲线

函 数RSNEMS硬阈值13．7700．0025软阈值12．0900．0025折中13．9300．0025对数13．6100．0025指数13．7500．0025新型阈值14．4000．0025

将各种小波阈值函数用于滚动轴承外圈故障振动信号的去噪过程,各种阈值方法的均方差没有变化,而新型小波阈值函数的信噪比最大,去噪效果较好.

6 结 论

(1) 提出了一种通过比较相邻两层细节信号的标准差从而确定小波分解层数的方法,获得了很好的去噪效果.

(2) 通过对几种小波阈值函数的仿真研究表明,新型小波阈值函数具有很好的平滑性和自然过渡性,对于两种仿真信号,去噪效果稳定,明显优于其他阈值函数.而其他小波阈值函数的去噪效果具有相当的信号敏感性.

(3) 将新型小波阈值函数用于对滚动轴承振动故障信号的去噪中,得到了比较好的效果,因此该新型小波阈值函数可用于类似信号的去噪.

[1] 操礼林,李爱群,邓扬,等.声发射和小波包分析在损伤状态监测中的应用[J].振动、测试与诊断,2012,32(4):591-598.

[2] 沈政伟,吴纪桃,廖福成.格结构的三带小波构造及在图像融合中的应用[J].北京科技大学学报,2012,34(10):1 218-1 226.

[3] 段晨东,高强,徐先峰.频率切片小波变换时频分析方法在发电机组故障诊断中的应用[J].中国电机工程学报,2013,33(32):96-105.

[4] 段锋,黄亚继,李斌,等.基于小波模极大值的湍动流态化流型转变特性研究[J].中国电机工程学报,2011,31(26):71-76.

[5] XU Y S,WEAVER J B,HEALY JR D M,etal.Wavelet transform domain filters:a spatially selective noise filtration technique[J].IEEE Transactions on Image Processing,1994,3(6):747-758.

[6] DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.

[7] 李士心,刘鲁源.基于小波阈值去噪方法的研究[ J].仪器仪表学报,2002,23(3):478-479.

[8] HE Can,XING Jianchun,LI Juelong.A new wavelet threshold determination method considering interscale correlation in signal denoising[J].Mathematical Problems in Engineering,2014(28):1-9.

[9] 李红延,周云龙,田峰,等.一种新的小波自适应阈值函数振动信号去噪算法术[J].仪器仪表学报,2015,36(10):2 200-2 208.

[10] 张维强,宋国乡.基于一种新的阈值函数的小波阈信号去噪[J].西安电子科技大学学报:自然科学版,2004,31(12):196-299.

[11] 苑津莎,张冬雪,李中.基于改进阈值法的小波去噪算法研究[J].华北电力大学学报,2010,37(5):92-97.

[12] 崔华,宋国乡.基于小波阈值去噪方法的阈值去噪方法一种改进方案[J].现代电子技术,2005(1):8-10.

[13] DONOHO D L,LAIN M J.Ideal spatial adaptation by wavelet shrinkage[J].Blometrika,1994,81(3):425-455.

(编辑 白林雪)

Simulation and Application of a New Wavelet Threshold Function

FAN Haizhe, WANG Hao, HAN Chunhui

(SchoolofEnergyandMechanicalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

A novel wavelet threshold function is established.Based on the test signals formed by typical signals and Gaussian white noise,the de-noising effects are simulated and compared for the traditional wavelet threshold function,the improved wavelet threshold function and new wavelet threshold function.The simulation results demonstrate that the signal-noise ratio and standard deviation of the new wavelet threshold function for the de-noised signals are optimum.In addition,the new wavelet threshold function is applied to investigate the de-noising effects of the actual vibration signals of rolling bearing.From the contrasts of time domain signals and signal-noise ratio of de-noising signals,the novel wavelet threshold function shows better de-noising effect,and signal-noise ratio is greatly improved.

wavelet threshold function; wavelet analysis; vibration signal; signal-noise ratio; rolling bearing

10.3969/j.issn.1006-4729.2017.03.012

2016-08-31

范海哲(1988-),女,在读硕士,吉林长春人.主要研究方向为风力机的故障诊断等.E-mail:haizhe.1028@163.com.

TN911.72;TN911.4

A

1006-4729(2017)03-0273-06