技巧显身手 妙解数列题

江苏 陆东标 韩文美

技巧显身手 妙解数列题

江苏 陆东标 韩文美

数列是一种特殊的函数，既包含有函数的一般性质特征，又具有其独特的特殊含义．在实际解决数列问题时，可以借助函数的一般技巧方法，又可以超出函数寻求其独特的技巧策略．特别在解答数列小题时结合一定的技巧与策略，巧妙借助一些技巧方法，往往可以使问题简单易懂，解答快捷方便，达到非常好的效果．特别在解决一些相关的高考数列选择题或填空题中，如果采用一些技巧，往往方法简单，思维巧妙，大大节约了宝贵的考试时间．

1．简单化技巧

在实际解答数列的一些选择题或填空题时，经常采用把数列的项、数列的项数、数列的通项等简单化，利用更为具体直观的简单化问题来求解具有一般情况的数列问题．

【例1】（2015·陕西文·13）中位数为1010的一组数构成等差数列，其末项为2015，则该数列的首项为．

【分析】具体数列的项不能确定，必须根据中位数的性质分奇偶项来分析，而通过简单化思维，直接考虑数列分别为3项、4项的情况即可，问题简单化，求解更为快捷．

【解析】由数列的项数简单化，当数列的项数为3项时，则有a1＋a3＝2a2＝2020，解得a1＝5；

当数列的项数为4项时，则有a1＋a4＝a2＋a3＝2020，解得a1＝5．

综合可知该数列的首项为5，故填5．

【点评】常规方法是根据中位数的求法，考虑数列的项数分别为奇偶数时，结合数列的性质建立相应的数列关系式，进而分析与求解．而通过数列的项数简单化，使问题进一步具体化、简单化，求解起来更具体、直观．

A．an＞an＋1

B．an＜an＋1

C．an＝an＋1

D．与n的取值相关

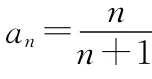
2．特殊化技巧

在实际解答数列的一些选择题或填空题时，我们有时可以尝试利用最简单可行的办法——特殊化来求解数列问题．可以用来解决数列的特殊项、数列运算等相关问题．

【例2】（2014·广东理·13）若等比数列｛an｝的各项均为正数，且a10a11＋a9a12＝2e5，则lna1＋lna2＋…＋lna20＝ ．

【分析】根据等比数列的相关性质计算时比较烦琐，而通过取特殊的等比数列——公比为q＝1的数列，可以使得计算更为简单快捷，又由特殊回归一般得到答案．

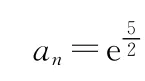
故填答案：50．

【点评】要直接计算或求解时难度比较大或计算比较烦琐，有时还可能无从下手，而通过取特殊数列、特殊项等特殊化技巧加以分析，并从中发现规律，进而得出答案．

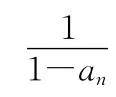
3．赋值化技巧

对于题设为一般状态，而结论为定值的问题，可以对题中的参数问题加以特殊赋值，可以赋以特殊数列、数列的特殊项进行代换，以特殊的赋值的结果替代一般的推理运算，从而得出答案．

【分析】根据题目条件，直接求解存在很大的难度，而通过依次赋值，结合相关项的值加以归纳得以确定规律，进而加以运算得到相关的答案．

【解析】由题意通过直接赋值可得b2＝3，b3＝4，b4＝5，a3＝3，a4＝4，

由不完全归纳可得an＝n，bn＝n＋1，

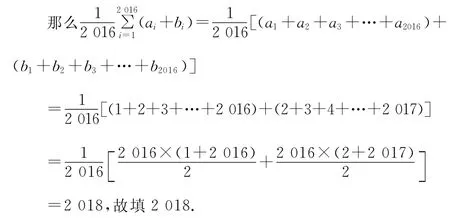
【点评】当相关数列的填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时，可以把题中变化的不定量用特殊值来赋值代替，即可以得到正确结果；对应数列的递推关系式问题也经常采用灵活赋值来分析．这里直接通过赋值化技巧确定数列｛an｝，｛bn｝的前几项，通过归纳得相应的通项后加以求解．

【变式3】（2016·浙江理·13）设数列｛an｝的前n项和为Sn．若S2＝4，an＋1＝2Sn＋1，，则a1＝________， S5＝________．

【解析】令n＝1，可得a2＝2a1＋1，

又S2＝a1＋a2＝4，解得a1＝1，a2＝3，

由an＋1＝2Sn＋1，可知a3＝2S2＋1＝9，则S3＝S2＋a3＝13，

同理a4＝2S3＋1＝27，则S4＝S3＋a4＝40；a5＝2S4＋1＝81，则S5＝S4＋a5＝121；

故填答案：1，121．

4．整体化技巧

把数列题中的一些式子视为一个整体，把它代入另一个式子，从整体思维上思考，便能化繁为简，得出答案．往往把数列中的一些项的整体、求和公式的整体等作为一个整体来加以研究．

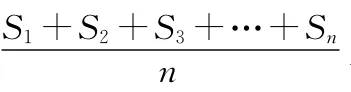
【分析】结合创新定义，非常巧妙地把式子S1＋S2＋S3＋…＋S99看作一个整体，利用整体思维与求和公式加以剖析，转化成式子S1＋S2＋S3＋…＋S99的代数运算形式，再利用相应的公式加以求解．

则有S1＋S2＋S3＋…＋S99＝99000，

则有100项的数列｛1，a1，a2，a3，…，a99｝的“凯森和”为

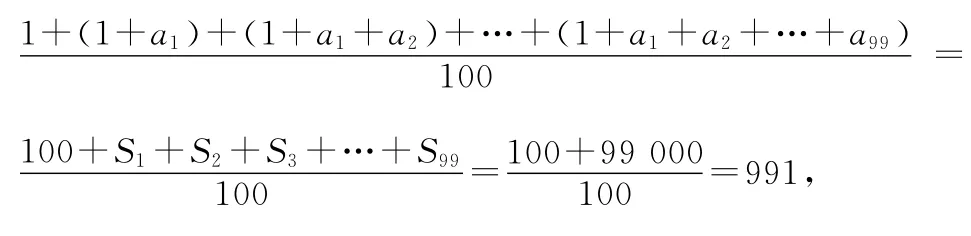
故填答案：991．

【点评】通过创新定义的应用，巧妙把相应的式子S1＋S2＋S3＋…＋S99整体化，结合新数列的运算加以转化，利用该整体式子的值加以分析与应用．整体化技巧在解决一些数列性质、创新定义、创新运算等数列问题时经常有上佳表现．

【变式4】（2015·新课标Ⅱ理·4）已知等比数列｛an｝满足a1＝3，a1＋a3＋a5＝21，则a3＋a5＋a7＝ （ ）

A．21 B．42

C．63 D．84

【解析】设等比数列｛an｝的公比为q，

则有a1＋a3＋a5＝a1＋a1q2＋a1q4＝21，

整理有q4＋q2－6＝0，解得q2＝2，

那么a3＋a5＋a7＝（a1＋a3＋a5）q2＝42，故选B．

5．拆分化技巧

涉及数列的一些通项问题时，往往可以通过对其通项加以合理转化，利用拆分化技巧，把通项加以巧妙拆分，再结合题目条件加以分析与求解．往往可以大大减少计算量，简化过程．

【例5】（2015·江苏·11）数列｛an｝满足a1＝1，且an＋1－an＝n＋1，则数列的前10项和为________．

【点评】通过巧妙拆分数列的通项，把有关分式的通项进行拆分，把通项拆分为两数式差的形式，再结合数列求和加以抵消达到简化运算的目的．

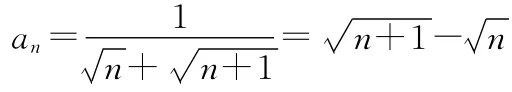
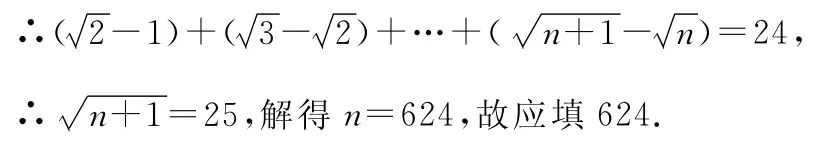
6．建模化技巧

建模构造是在解决一些数列填空题时，可以根据题设有关数列的条件与结论的特殊性，构造出一些新的数学形式（例如直观几何模型、函数、特殊数列、方程等），并借助于它认识和解决问题的一种方法．

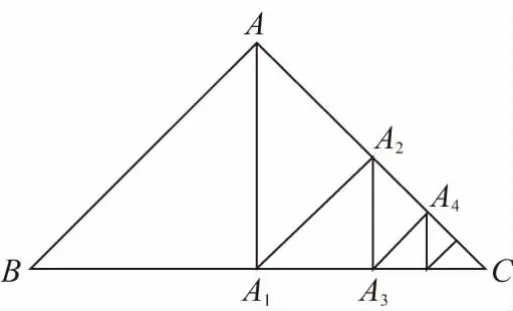
【例6】如图，在等腰直角三角形ABC中，斜边BC＝，过点A作BC的垂线，垂足为A1；过点A1作AC的垂线，垂足为A2；过点A2作A1C的垂线，垂足为A3；……，依次类推，设BA＝a1，AA1＝a2，A1A2＝a3，…，A5A6＝a7，…，则a2017＝________．

【分析】结合等腰直角三角形的性质，根据对应的三角形的直角边构成等比数列的关系，建构模型，结合等比数列的递推关系与通项关系来分析，并通过归纳推理来求解．

【点评】本题考查了图表的表示、分析与处理，等比数列的应用，归纳与推理，建构模型等．关键是通过建构模型，利用图表表示形式引入，利用等腰直角三角形的直角边间的特征规律加以探究分析，进而归纳出一般性的规律，从而得以解决相应的问题．此类数列问题解决的基本思路是：递推→通项→求值（和、积等）．

【变式6】（2014·安徽文·12）如图，在等腰直角三角形ABC中，斜边，过点A作BC的垂线，垂足为A1；过点A1作AC的垂线，垂足为A2；过点A2作A1C的垂线，垂足为A3；依此类推，设BA＝a1，AA1＝a2，A1A2＝a3，…，A5A6＝a7，则a7＝________．

解答数列小题中，关键是抓住等差数列或等比数列的定义、公式与相关性质加以分析与处理，特别碰到一些计算量大、创新性强、信息量多的数列问题时，可以抓住题目本质，从定义、性质等方面入手，使问题简单化，通过以上一些相关的技巧方法入手加以辅助解决，往往可以使得数列小题的解答显得更为简单快捷，处理起来更为顺手，同时可以简化运算，提升解题速度，提高解题效率．

（作者单位：江苏省张家港职业教育中心校）