高考易错题自测卷
——解析几何
江苏 尚建敏浙江 张永兵
高考易错题自测卷
——解析几何
江苏 尚建敏浙江 张永兵
一、选择题
1.经过点(2,-1)且在两坐标轴上的截距相等的直线方程为 ( )
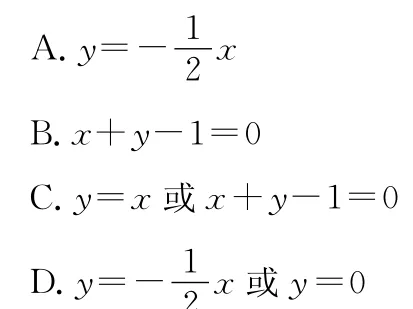
2.已知直线l1:x+ay-1=0,l2:a2x-y+3=0(a∈R),若l1⊥l2,则a的值是 ( )
A.0 B.1
C.0或1 D.-1或1
3.以点(5,0),(0,5)为端点的线段的方程为 ( )
A.x-y-5=0
B.x+y+5=0
C.x+y-5=0(0<x<5)
D.x+y-5=0(0≤x≤5)
4.过点(1,1)的直线与圆x2+y2-4x-6y+4=0相交于A、B两点,则|AB|的最小值为 ( )

5.已知F1、F2为两个定点,动点P满足|PF1|+|PF2|=10,则动点P的轨迹是 ( )
A.椭圆 B.圆
C.线段 D.不确定
A.4 B.12
C.16 D.48

8.设抛物线y2=mx(m≠0)的准线与直线x=1的距离为3,则抛物线方程为 ( )
A.y2=-8x
B.y2=-16x
C.y2=-8x或y2=16x
D.y2=8x或y2=-16x

10.若动点M与两个定点A(3,0),B(-3,0)构成的三角形周长为16,则动点M的轨迹方程为 ( )
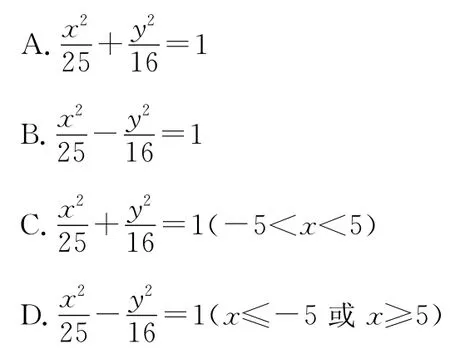
二、填空题
12.等腰三角形的顶点A(-4,0),底边一个端点B的坐标为,则另一个端点P的轨迹方程为_______.
13.已知实数x、y满足方程x2+y2-4x+1=0,则z=y-x 的最大值和最小值分别为_______.
14.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆的方程为_____________.
15.双曲线x2-y2=16的左焦点为F1,点P在双曲线上,若|PF1|=10,则|PF2|=________.
16.已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0),B(m,0),m>0,若圆上存在点P,使得∠APB=90°,则m 的取值范围是_______.
18.过点(0,1)的直线且与抛物线y2=2x仅有一个交点的直线方程为____________.
19.已知A是抛物线y2=4x上一点,F是抛物线的焦点,直线FA交抛物线的准线于点B(点B在x轴上方),若|AB|=2|AF|,则点A 的坐标为_______.
20.已知动圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,则动圆圆心M的轨迹方程为____________.
【参考答案与提示】
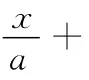
2.C 【解析】因为l1⊥l2,所以a2-a=0,解得a=0或a=1,故选C.
【易错警示】由斜率乘积等于-1得到a的值是-1,忽略了直线l1的斜率不存在的情况.
3.D 【解析】以点(5,0),(0,5)为端点的线段的方程为x+y-5=0(0≤x≤5).
【易错警示】不注意线段与直线方程的区别.

【易错警示】不能区别弦长与弦心距,把求最小值当作求最大值.
5.D 【解析】依题意,①当|F1F2|<10时,动点P的轨迹是以F1、F2为焦点的椭圆;②当|F1F2|=10,动点P的轨迹是线段|F1F2|;③|F1F2|>10,动点P的轨迹不存在.故选D.
【易错警示】对椭圆的定义理解不透彻,误以为点P到两定点的距离之和为常数的点的轨迹一定是椭圆.
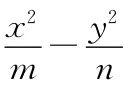
所以m+n=16,
解方程组
所以mn=48,故选D.
7.C 【解析】①当椭圆的焦点在x轴上,因为a2=2,b2=m,所以c2=2-m,
②当椭圆的焦点在y轴上,由题意得b2=2,a2=m,所以c2=m-2,
【易错警示】由于2与m的大小关系不确定,椭圆的焦点可能在x轴或y轴上,需要分类讨论.

【易错警示】忽视m<0的情况,注意:抛物线y2=2px(p>0)开口向右,抛物线y2=-2px(p>0)开口向左.
得(x-2)2+(y-3)2=4(1≤y≤3),如图所示,

10.C 【解析】因为A、B是两定点,|AB|=6.
又三角形的周长为16,所以|MA|+|MB|=10.

其中2a=10,2c=6,即a=5,c=3,
所以b2=a2-c2=25-9=16,
因此应去掉椭圆在x轴上的两个端点,
11.直线x=1和射线x+y-1=0(x≥1) 【解析】由方程得或,则x+y-1=0(x≥1)或x-1=0,故原方程的曲线表示直线x=1和射线x+y-1=0(x≥1).
【易错警示】注意二次根式的被开方式应大于或等于0,所以求出的是曲线的一部分.
12.(x+4)2+y2=36(x≠-10且x≠2) 【解析】根据题意,由等腰三角形的特征,设P(x,y),由PA=AB,得,
则另一个端点P的轨迹方程(x+4)2+y2=36.
因为△PAB必存在,所以P、A、B不共线,
所以x≠-10且x≠2,
故点P的轨迹方程(x+4)2+y2=36(x≠-10且x≠2).
【易错警示】因为△PAB必存在,所以P、A、B不共线,所以注意x的取值范围是x≠-10且x≠2.【解析】z看作是直线y= x+z在y轴上的截距,当直线y=x+z与圆相切时,纵截距z取得最大值或最小值,此时,解得z=或,所以z的最大值为,最小值为.
【易错警示】不理解z的几何意义,或用点到直线的距离公式时漏掉绝对值符号.
【易错警示】忽视焦点的位置,只求出一个方程.
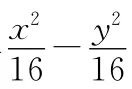
因为|PF1|=10,由||PF1|-|PF2||=2a=8,
得|PF2|=10-8=2或|PF2|=10+8=18.
所以|PF2|=2或18.
【易错警示】对双曲线的定义理解出错,把||PF1|-|PF2||写成|PF1|-|PF2|只能求出一个结果.
16.[4,6] 【解析】由已知以AB为直径的圆与圆C有公共点,AB中点为原点,|AB|=2m,则|m-1|≤,解得4≤m≤6,故m的取值范围是[4,6].
【易错警示】漏掉不等式中的等号.
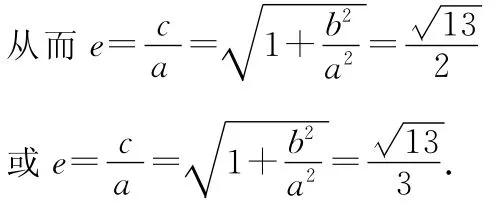
②当所求直线斜率k=0时,直线为y=1,平行于x轴,它正好与抛物线y2=2x只有一个交点;
③当k≠0时,设所求的过点(0,1)的直线为y=kx+1,

【易错警示】忽视k=0与斜率不存在的情形,对于直线与抛物线“相切”和“只有一个交点”理解不透彻.
由
②若点A位于x轴下方,则此时点F(1,0)是线段AB的中点,
又点B的横坐标是-1,
【易错警示】忽视点A在x轴下方的情况,导致得到的答案不全面.
又C1(-4,0),C2(4,0),所以|C1C2|=8,
根据双曲线定义知,点M的轨迹是以C1(-4,0),C2(4,0)为焦点的双曲线的右支.
所以b2=c2-a2=14,
【易错警示】不能区别||MC1|-|MC2||与|MC1|-|MC2|的含义;写方程时忽视了限制条件.
(作者单位:江苏省赣榆县海头高级中学,浙江省杭州市黄公望高级中学)

