与动量知识结合的易错问题分析

湖北 许 文

与动量知识结合的易错问题分析

湖北 许 文

学习中防止出现错误，才能取得进步。认识每一道错题背后可能隐藏的知识上的疏漏、理解上的偏差，透过错误表象看到其本质，往往比正确做出一道题收效更大。2017年全国高考物理大纲将动量知识内容调整为必考内容，这一调整必将在高考中有所体现。本文分析高考中与动量知识结合的易错问题，做到有的放矢，科学备考。

一、用动量定理分析持续作用问题建模致错

【例1】如图1所示，一架质量为M的武装直升机武直－10的旋翼桨旋转向下推空气获得反冲力使直升机悬停在空中。已知向下推出空气的速度为v，则直升机发动机的功率为 （ ）

图1

【错解】因直升机悬停在空中，旋翼桨旋转向下推空气获得反冲力F＝Mg，则直升机发动机的功率为P＝Fv＝Mgv，B项正确。

【错因】直升机发动机带动旋翼桨旋转持续向下推空气使其获得反冲力，发动机的平均功率是指旋翼桨对推出空气做功的平均功率。以上错解在于不能对持续作用问题正确建立物理模型。

【正解】在本题的求解过程中，我们可以构建这样一个物理模型：设发动机带动旋翼桨旋转一段很短的时间Δt，使质量为Δm的一团空气体获得向下的速度v，发动机对这团气体的作用力为F（FΔmg），直升机获得反冲力F′而停在空中不动。发动机在这段时间内对这团气体所做的功ΔW应等于这团气体的动能的增量，即

对直升机有F′＝Mg

对这团气体由动量定理有 （F＋Δmg）Δt＝Δmv，

由于FΔmg，上式可以变为FΔt＝Δmv

由牛顿第三定律得F与F′的大小应相等，即F＝F′

【答案】C

【感悟】持续作用问题又称流体问题。液体流、电子流、光子流、气体流等被广义地称为“流体”，其中电子流、光子流、气体流等又可统称为粒子流。对于流体的持续作用问题，关键的是正确建立物理模型，选取合适的研究对象。

持续作用问题的求解要点：

（1）确定研究对象：选取研究对象的方法通常用到微元法。对液体流，通常选取质量为Δm的一段液柱为研究对象；对于运动粒子流，通常是选取体积为ΔV的体积元为研究对象。

（2）选取作用时间：选取持续作用过程中一段很短的时间Δt。注意这段Δt内发生作用的“流体元”的质量Δm很小，必要时这一条件是采用相关数学近似计算的依据。

（3）选用相关规律：一般可用动量定理，也可用牛顿运动定律与相关运动学公式。值得注意的是，在很短的作用时间Δt内，研究对象“流体元”受到的作用力可以认为是不变的，或取作用力的平均值。动量定理的表达式是一个矢量式，可以用在某个方向上，应用时要注意相关矢量正方向的选取。

二、动量与能量相结合时对暂态过程分析不清致错

【例2】如图2所示，A、B、C三个木块的质量均为m，置于光滑的水平桌面上，B、C之间有一轻质弹簧，弹簧的两端与木块接触而不固连。将弹簧压紧到不能再压缩时用细线（细线未画出）把B和C紧连。现A以初速度v0沿B、C的连线方向朝B运动，与B相碰并黏合在一起，之后细线突然断开，弹簧伸展，从而使C与A、B分离。已知C离开弹簧后的速度恰为v0，求弹簧释放的势能。

图2

【错解】设A与B碰后A、B的共同速度的大小为v，由动量守恒定律得mv0＝2mv①

设C离开弹簧时，A、B的速度大小为v1，由动量守恒定律得2mv＝2mv1＋mv0②

设弹簧释放的弹性势能为Ep，从细线断开到C与弹簧分开的过程中系统机械能守恒，有

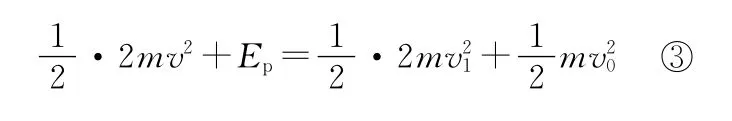
【错因】由于题给出“B和C间的弹簧压紧到不能再压缩”，在A与B碰撞瞬间，也存在B与C碰撞这样一个暂态作用过程，可等效为A与B、C一起碰撞。以上错解没能认清这个暂态作用过程，致使列出的表达式①②③式均有错误，因而得出的结果错误。

【正解】设A与B、C碰后A、B、C的共同速度的大小为v，由动量守恒定律得mv0＝3mv①

设C离开弹簧时，A、B的速度大小为v1，由动量守恒定律得3mv＝2mv1＋mv0②

设弹簧的弹性势能为Ep，从细线断开到C与弹簧分开的过程中机械能守恒，有

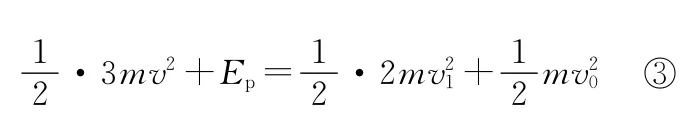
【感悟】刚性物体间的碰撞是一个暂态作用过程。对这个暂态过程的分析，一般可从动量的观点和能量的观点来进行。由于这两个观点研究的是物体或系统运动变化所经历过程中状态的改变，不对过程变化的细节做深入的研究，只关心运动状态变化的结果及引起变化的原因。因而就很容易忽视对暂态过程的分析。含有弹簧的碰撞问题，在碰撞过程中系统的机械能不一定守恒，如本例中，弹簧伸展之前，A与B碰撞的过程为完全非弹性碰撞，但在碰撞结束后，弹簧伸展的过程中，系统的动量和机械能均守恒。

三、动量守恒定律应用于原子能级跃迁因机理不明确致错

【例3】用电子碰撞静止的原子，能使原子从基态跃迁到激发态。设电子质量为m，原子质量为M，原子基态与激发态的能量差为ΔE，求入射电子初动能的最小值。

【错解】设入射电子的初动能为Ek，则初动量大小为与静止的原子碰撞后原子的速度为v，碰后电子的速度为零时，Ek最小。由动量守恒定律得，由能量守恒定律得，联立以上两式可得

【错因】以上错解在于对原子能级跃迁的机理不明确。电子碰撞静止的原子，原子只吸收电子的部分能量而不是全部，因此碰后电子的速度不可能为零。

【正解】设入射电子的初动能为Ek，则初动量大小为与静止的原子碰撞后电子的速度为u，原子的速度为v。由动量守恒定律得

【感悟】能量守恒定律与动量守恒定律是自然界中最普遍的规律，它们不仅适用于宏观低速运动的物体，也适用于微观高速运动的粒子。本题的求解要建立正确的物理情景：电子与原子的“碰撞”过程中损失的机械能被原子吸收，等于基态的原子跃迁到激发态而增加的原子能量。由于题给出的这一能量是个定值，由能量守恒定律知入射电子的初动能与碰撞后电子或原子的速度大小有关。通过运用两个守恒定律导出电子初动能与碰后电子或原子的速度大小的表达式，再运用数学知识求极值。

（作者单位：湖北省武汉市华北科技大学附属中学）