焊接机器人运动控制算法研究

韩沛文，周 靖，蒋 林，张金泳

（深圳市鸿栢科技实业有限公司，深圳 518105）

焊接机器人运动控制算法研究

韩沛文，周 靖，蒋 林，张金泳

（深圳市鸿栢科技实业有限公司，深圳 518105）

运动控制系统是决定焊接机器人性能的关键部件之一。针对焊接机器人的作业要求和特点，探讨了改进焊接机器人性能的运动控制算法，包括6关节串联型焊接机器人运动学，运动平滑加减速规划，运动插补，速度前瞻算法等。力图摆脱国产机器人在核心技术方面受制于人，落后挨打的局面。基于OpenGL（Open Graphics Library）的虚拟机器人模拟仿真以及实际机器人作业级实验结果，证明提出的算法是有效的，可用于国产焊接机器人的运动控制系统。

焊接机器人；样条加减速规划；运动插补；速度前瞻；重力矩补偿

0 引言

焊接机器人具有焊接质量稳定、改善工人劳动条件、提高劳动生产率等特点，因此被广泛应用于汽车、工程机械、通用机械、金属结构和兵器工业等行业。据不完全统计，全世界在役的工业机器人中大约有一半用于各种形式的焊接加工领域[1]。目前，国内焊接机器人应用市场可分为日系、欧美系和国产三类。其中日系主要以安川MOTOMAN（如MOTOMAN-ES165D）、OTC（如FD_V166）、松下（如VR-006L）、FANUC（如R-2000iB/165F）等机器人为主；欧美系以德国的KUKA（如KR-150R3100PRIME）、CLOOS（如ROMAT350）、瑞士的ABB（如IRB6650S）以及奥地利的IGM（如RTE499）机器人等；国产焊接机器人主要以沈阳新松机器人、广州数控机器人为主。和国外产品相比，国产焊接机器人在价格和性能两个方面都处于劣势。究其根本原因，就是在焊接机器人系统的关键技术特别是运动控制技术方面没有突破，且落后于人，受制于人[1,2]。

运动控制系统是决定焊接机器人性能的关键部件之一。运动控制算法又是确定运动控制系统特性提高企业竞争力的核心技术[3,4]。所以，研究稳定、高效、适合焊接机器人作业的运动控制系统，特别是核心算法，是国产焊接机器人摆脱落后局面，提高竞争力，抢占行业市场先机的关键。

本文将从焊接机器人运动控制系统组成、机器人运动学、运动加减速规划、运动插补、速度前瞻、重力矩补偿等方面，阐述改善和提高焊接机器人性能的运动控制算法，并给出算法的计算机仿真和在一种原型机器人上的实验结果。

1 焊接机器人运动控制系统

如图1所示，焊接机器人运动控制系统主要由程序解释器、运动插补器、伺服驱动器以及其他一些辅助模块组成。其中运动插补器相当于人类的大脑智慧部分，它接收用户程序指令解释器输出的运动控制指令，并根据指令附带的技术要求，精心规划出位置或轨迹运动参数，交给驱动伺服器执行。可见运动插补是焊接机器人运动控制系统的核心技术。它主要包含机器人运动学、运动加减速规划、运动插补、速度前瞻、重力补偿、焊缝跟踪和多机协调等核心算法。限于篇幅，以下仅研究机器人运动学、运动加减速规划、运动插补、速度前瞻算法。有关重力补偿、焊缝跟踪和多机协调核心算法，将在后续的文章中表述。

2 运动控制核心算法

焊接机器人手末端通常装有焊钳，其重量可达几百公斤。这种大载荷对垂直6关节串联型焊接机器人（如图2所示）的运动控制提出更加严格的要求。首先，机器人焊接作业运动在笛卡尔空间，而伺服位置控制在关节空间，为实现焊接作业运动控制，必须解决笛卡尔空间坐标到关节空间的变换问题（逆运动变换），或者关节空间坐标到笛卡尔空间坐标间的变换问题（正运动变换）。其次，由于6关节串联型机器人的结构在作业时位姿（位置和姿态）变化巨大，这对于大载荷的焊接机器人意味着任何加速度的突变都会产生较大的力或力矩突变，最终引起工具的振动，降低焊接质量。为此必须研究适应此种作业要求的平滑加减速规划算法。再次，弧焊机器人在处理多段连续轨迹的焊缝时，为提高焊接效率和质量，必须研究相邻线段交接点的轨迹速度和加速度问题（速度前瞻）。最后，机器人杆件的重力和载荷对关节电机的力矩随作业位姿变化而变化，研究这种变化有利于改善焊接机器人的动态特性。

图1 焊接机器人运动控制系统

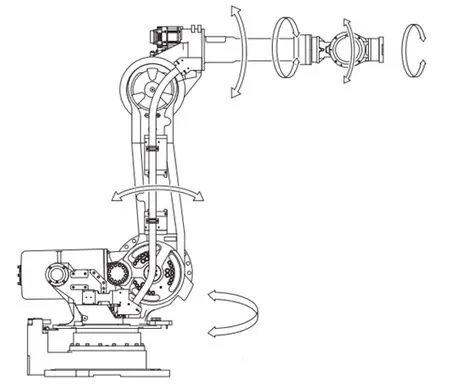
图2 垂直6关节串联型焊接机器人本体

2.1 机器人运动学

机器人运动学主要解决笛卡尔空间运动到关节空间（或者相反）的变换。由于正运动学比较直接，本文仅讨论垂直6关节串联型焊接机器人的逆运动学求解算法。

图3为相应图2采用DH方法[5]建立的杆件坐标系。表1为与图3对应的DH参数表。

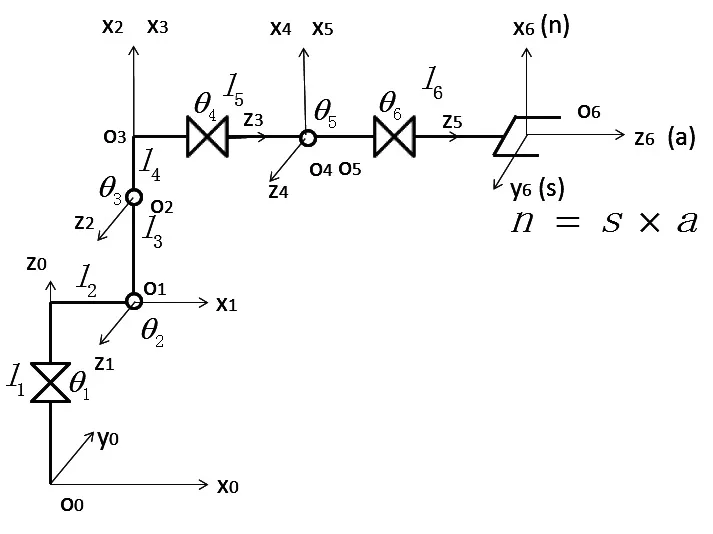
图3 机器人杆件坐标系

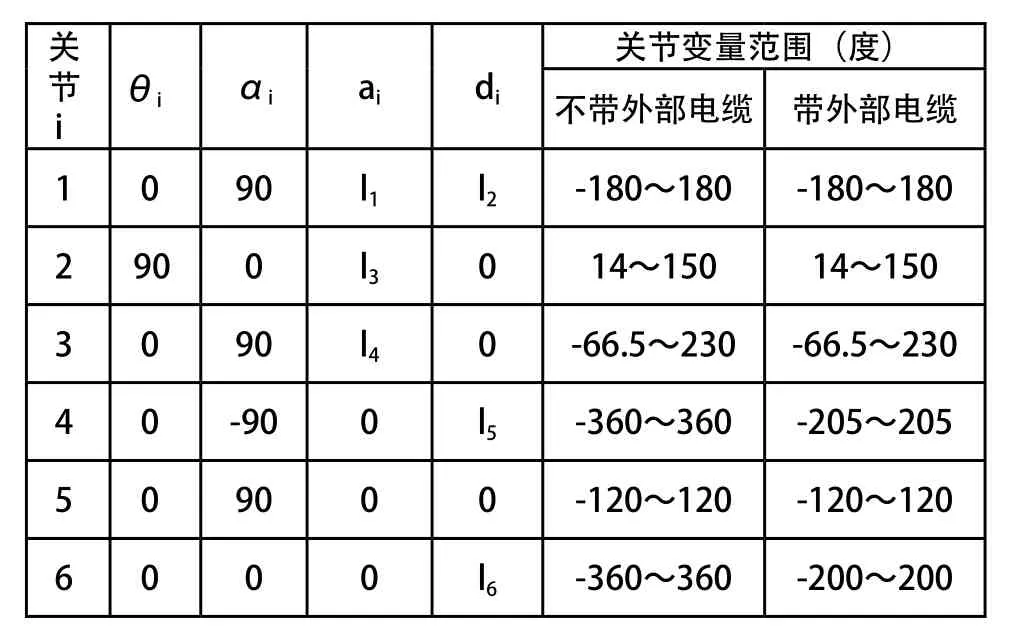
表1 网络拓扑结构图

其中，θi,i=1,2,…,6为关节角位移；1i,i=1,2,…,6为杆件长度；机器人手末端（法兰盘中心）的位置p=[px,py,pz]T，姿态向量为n,s,a。

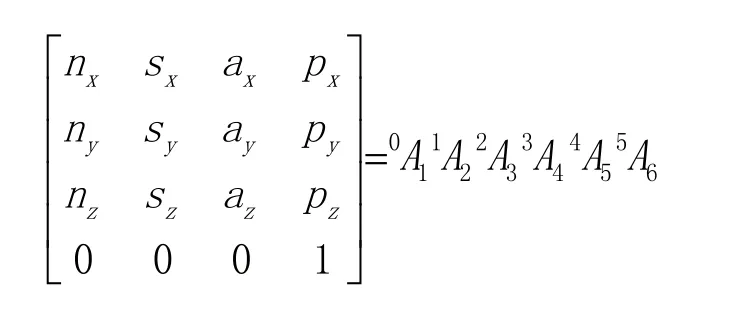
解出，速度和加速度可借助雅可比矩阵求出。以下是位移解。

上述算法在实际应用时还需考虑以下约束：运动的连续性；实际关节角的运动范围；实际关节角的运动区间。

特别注意，算法中使用了atan2(Dy,Dx)函数，这个函数数在Dy=Dy=0时可能会出现退化情况，即可能有无数组解。此种情况，一种选择是令当前解等于上一时刻的对应值。另一种选择是继续计算下一时刻的解，然后利用插值求解出当前的解。

此外，实际作业时，要求机器人工具姿态的变化是连续平稳的，且姿态的描述通常采用3个欧拉角来描述[5]，所以，需要姿态n,s,a向量转换成欧拉角。这样，运动插补就包括位置和姿态插补两个部分，且插补计算是类似的。

2.2 运动加减速规划

作业空间（笛卡尔空间）运动的平稳性是保证焊接机器人焊接质量的基本要求。为了克服加速度的突变对焊接机器人工具的冲击，必须考虑笛卡尔空间加速度二阶光滑连续的速度曲线规划算法。因为要求加速度二阶光滑连续，所以采用了三次多项式样条加减速速度曲线，该速度可保证曲线在每个运动段的加速度曲线是二阶光滑连续的。图4中从上到下，依次为位移、速度和加速度曲线。设采样周期为T，单位为秒，可求出时域内相应的数学表达式(7)～式(9)。

图4 三次多项式样条加减速速度曲线

2.3 运动插补

运动插补是将笛卡尔空间的位置和姿态运动分解到关节轴运动。由于焊接作业在笛卡尔空间，所以运动的平稳性要就也是针对笛卡尔空间，自然运动的加减速规划也在笛卡尔空间。但焊接作业的运动是各关节电机的复合运动来实现的。换言之，在任一采样时刻，所有参与运动的关节电机所组成的复合运动位置必须在对应时刻的作业轨迹上。为了保证这一点，通常需要先对笛卡尔空间的作业轨迹进行加减速规划，以保证加速度平滑性要求（可通过调用式(7)～式(9)来实现）。进而通过调用上述逆运动学方程（式(1)～式(6)）来求解与作业轨迹上的采样点相对应的各关节电机的位置、速度和加速度，并将这些运动参数作为目标位姿交给伺服驱动器执行位置闭环控制，最终实现机器人工具沿指定的作业轨迹运动，完成焊接作业。这种先加减速计算后插补计算的方法，是目前运动插补器通常采用的有效算法。

2.4 速度前瞻

在机器人实际生产作业中（例如弧焊作业），工具的控制点（TCP）的加工轨迹往往由连续的线段（通常是直线和圆弧）组成。此时TCP的轨迹为连续运动轨迹（Continuous Path or Contouring）。为提高加工质量和效率，必须考虑当TCP不在起始点和终止点时，根据加工轮廓轨迹的几何性质、运动约束和加工的要求来确定各控制点（即相邻线段交点）的速度，以控制TCP准确、平稳的跟踪预定的加工轨迹。否则在线段的交接处会产生速度突变，进而造成工具抖动，甚至出现过切，影响作业质量。解决这一问题的有效方法之一是采用速度前瞻技术。

速度前瞻控制主要是指插补过程中的轨迹前瞻控制，是随着数控加工技术向高速高精度发展而出现的一种新的控制方法。其基本思想是对插补轮廓轨迹进行预处理，包括分析组成插补轮廓各线段交接处的几何特性，并根据几何特性和运动约束（线段长度、线段的交角、最大速度、最大加速度、最大加加速度等）对加工路径的速度进行规划，保证加工时能够以适当的速度通过相邻线段的交接点，以减少在插补过程中速度变化引起的冲击，提高加工效率和质量。

为实现轨迹速度前瞻控制，需解决两个关键问题，一是减速特征识别，二是进给速度前瞻处理。考虑如图5所示的连续轨迹运动。当机器人的工具控制点从li段运动到li+1段时，在两运动段的交点会出现速度方向的变化，其变化的大小可用i来表示。由于因此产生的加速度不能超过给定的最大加速度，所以在两运动段的交点的速度vi必须满足式(10)。

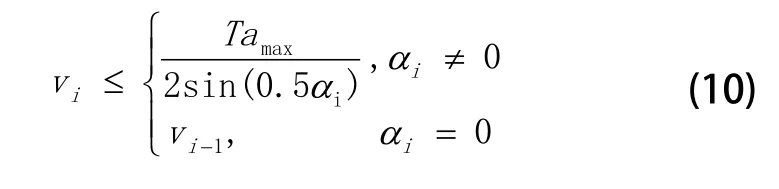
式中T为采样周期。

又由于机器人的工具控制点在圆弧段li+1段运动时会产生向心及速度，所以对于给定的最大向心加速度amax，vi还必须满足式(11)。

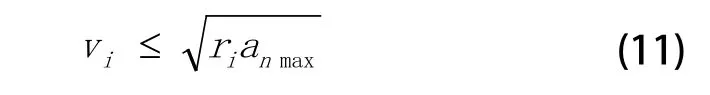
式(10)和式(11)的意义在于，机器人工具控制点在经过除起始点和终止点以外的各线段的交点时，不必减速到零，而是减速到作业允许的值，这样可以提高效率。这种根据运动线段交接的几何特性和作业要求来计算交接点的速度，就是减速特征识别。

速度前瞻则考虑当给定最大加速度和线段长度约束时，相对某些控制点，需要提前减速的问题。从速度规划来考虑，通常一个运动段包含加速、恒速和减速三个阶段。对于给定的速度、加速度约束，随着运动距离的减小，可能就没有恒速区，甚至只剩下加速区或减速区。另一方面，为使得运动平稳，必须有加减速过程。也即对于给定的速度、加速度约束，运动距离太短，会使速度规划不能实现。或者规划的速度曲线不能满足加速度约束，导致加速度过大，在这些小线段处产生冲击。为克服此种情况，应当保证实际的运动线段长度大于或等于规划线段的最小弧长。如图6所示。

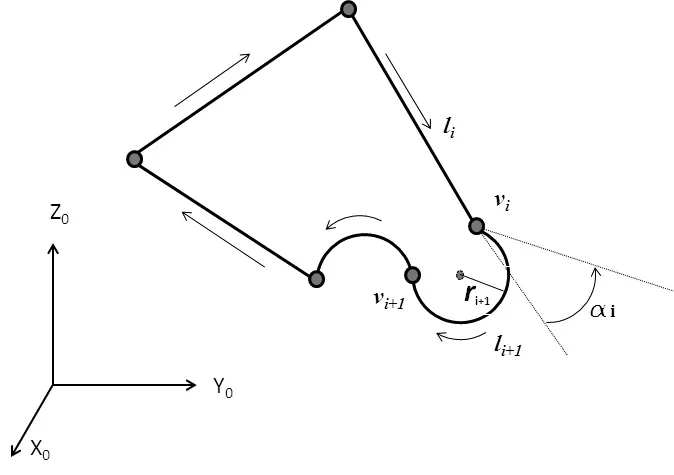
图5 连续插补与减速特征识别

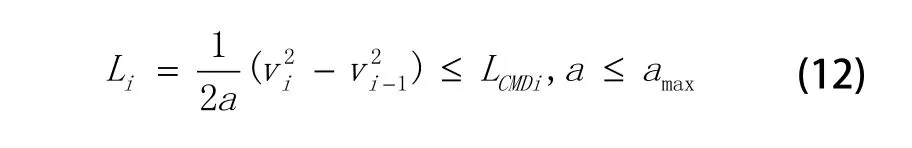
式中，Li为给定运动参数决定的弧长，LCMDi为指令运动段弧长。

当式(12)满足时，对应线段的速度规划是平稳的。当这个条件不能满足时，对于给定的线段弧长和加速度约束，就需要调整对应线段的起始或终止速度。注意到，任何一个轮廓轨迹运动，在物理上要求结束段终点的速度、加速度和加加速度均为零。为保证运动能够平稳停止，可从轮廓轨迹的结束段开始，回溯整个时间历程，对每一运动段进行上述检查，必要时进行调整，如此即可保证整个轮廓连续运动的平稳性和高效率。此过程就是速度前瞻。

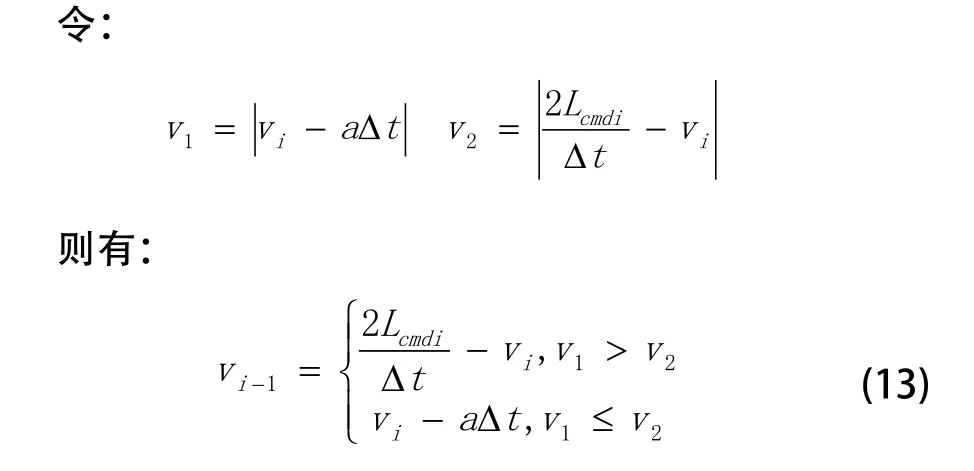
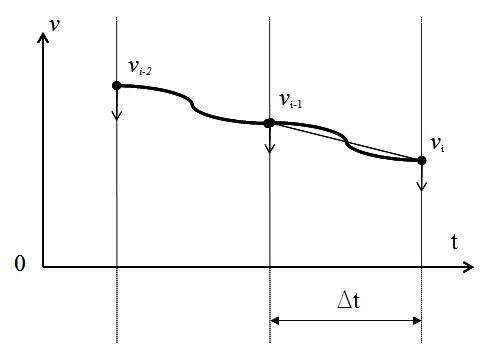
图6 连续插补与速度前瞻

3 计算机仿真

本文算法在OpenGL虚拟机器人上进行了计算机仿真。图7为应用本文机器人运动学算法在虚拟机器人上实现单段螺旋运动的情况。图8为应用本文机器人运动学算法以及速度前瞻算法在虚拟机器人上实现多段连续轨迹运动的情况。仿真结果与期望结果完全一致。

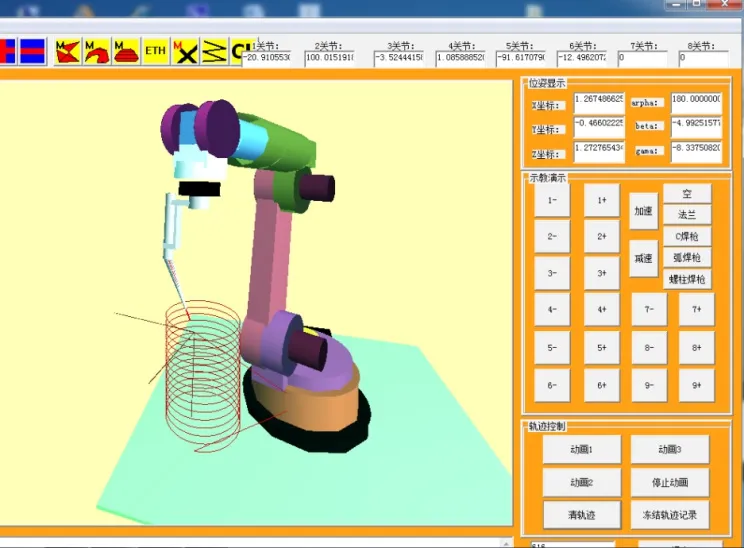
图7 焊接机器人逆运动学算法计算机模拟

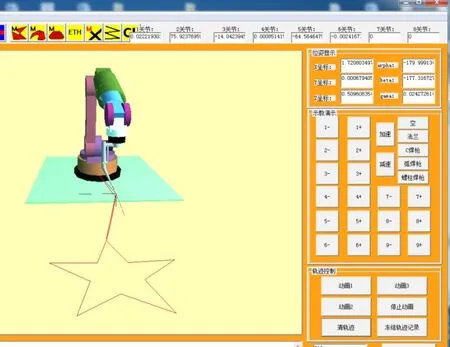
图8 焊接机器人速度前瞻算法计算机模拟

4 机器人实验

为进一步验证实际效果，本文算法在一个特制的负载为2kg的原型机器人上进行了实际测试。图9为模拟弧焊作业完成相贯线的焊接实验。图10为模拟弧焊作业完成多段连续轨迹的焊接实验。实验结果与期望结果完全吻合。

图9 焊接机器人弧焊作业实验

图10 焊接机器人连续轨迹速度前瞻实验

5 结论

针对焊接机器人的作业要求，研究了焊接机器人运动控制系统的核心算法。给出了垂直六关节串联型焊接机器人的逆运动学、三次多项式样条加减速速度规划、速度前瞻算法。计算机仿真和模型机器人实验验证了算法的有效性。可用于焊接机器人的运动控制系统，提高和改善焊接机器人的作业性能。

[1] 宋天虎,张军.关于中国焊接机器人发展的粗浅思考[J].焊接,2014(8):1-3.

[2] 刘占起,李子木.焊接机器人技术发展现状与趋势[J].现代焊接,2016(2).

[3] Y. Z. Du,X. L. Ping, L. G. Chen, W. B. Xu. Motion Control of Welding Robot Based on ADAMS and ACR-9000[J].Advanced Materials Research,2012,542-543:789-794.

[4] Q. Wu, J. Wu. A Control System Based on ARM and Motion Controller for Arc Welding Machine[J].Advanced Materials Research, 2014,889-890:1121-1125.

[5] 付京逊,R.C.冈萨雷斯,C.S.G.李.机器人学[M].杨静宇,等译.北京:中国科学技术出版社,1989:4.

Research on motion control algorithms for welding robots

HAN Pei-wen, ZHOU Jing, JIANG Lin, ZHANG Jin-yong

TP241

：A

1009-0134(2017)07-0152-05

2017-05-31

深圳市科技计划技术攻关重点项目（JSGG20160301151929860）

韩沛文（1984 -），男，安徽定远人，硕士，研究方向为焊接机器人。