重型机床立柱结合面应力研究

陈 浩，齐向阳，史 凯，田尚沛

（天津工业大学 机械工程学院，天津 300387）

重型机床立柱结合面应力研究

陈 浩，齐向阳，史 凯，田尚沛

（天津工业大学 机械工程学院，天津 300387）

鉴于重型机床体型庞大、重量大、加工和装配精度不好保证的情况，以重型龙门铣床立柱为例，分析讨论了立柱结合面在不同压力、扭矩、表面粗糙度、平面度情况下的装配应力变化情况。结果表明结合面表面粗糙度、平面度对结合面的影响较大，且有较为明显的线性关系，横梁自重次之，装配扭矩对结合面影响最小。该结果可以为机床立柱设计优化和装配提供依据，最终实现重型机床运动过程中的高精度特性。

重型机床；静态特性；有限元模拟；结合面特性参数；应力

0 引言

机床制造业作为机械制造行业的核心，已经成为衡量一个国家机械制造水平的重要标志，重型机床的高可靠性和高精度已经成为研究的重点。机床结合面作为机床结构的一个重要参数，在装配过程和运动过程中，结合面之间的应力会随之变化的，从而影响到机床整体的精度，重型机床尤为突出。因此，结合面特征参数的有效识别对于优化结构具有重要意义。本文鉴于重型龙门铣床存在横梁自重过大、双立柱不平行不共面产生的装配扭矩、结合面间加工误差所造成的装配应力，分析讨论了重型龙门铣床立柱结合面在不同压力、扭矩、表面粗糙度、平面度情况下的装配应力、变形情况。Levina[9]研究了结合面的平面度误差给结合面接触刚度带来的影响，Masuko[10]进一步肯定了切向载荷与切向接触刚度的关系。

1 结合面接触参数分形模型的构建

近年来研究表明[1]影响结构结合面静态特性的因素可以分为以下三类：

1）影响结构的因素，如零件结合面的尺寸与类型、功能、形状误差等；

2）影响工况的因素，如零件结合面上的静载荷等；

3）影响结合面固有特性的因素，如结合面表面的粗糙度，结合面的预面压、零件的材料属性、加工所需要的方法以及结合面之间的介质等。

从Majumdar[7,8]等人的研究表明，机械零件的接触表面都具有自仿射分形的表面特征，并提出了基于分形理论为研究基础的表面接触模型（简称MB模型）[7,8]。在MB模型，先假设零件的粗糙表面具有各向同性的形貌，忽略由弹性变形到塑性变形转换所引起的加工硬化，且随着距离材料表面深度的变化，材料硬度不变，在粗糙表面上，假设零件粗糙表面的接触是一个理想的平面与一个粗糙的表面的接触。在微观尺度上，结合面的两表面都存在着大量的微凸体，结合面的相互接触实际上就是微凸体之间的相互接触作用结果。因此，首先得研究理想平面与粗糙表面接触的接触性质，然后再确定单个微凸体与刚性理想平面的接触性质，然后再建立微凸体的理想接触模型。

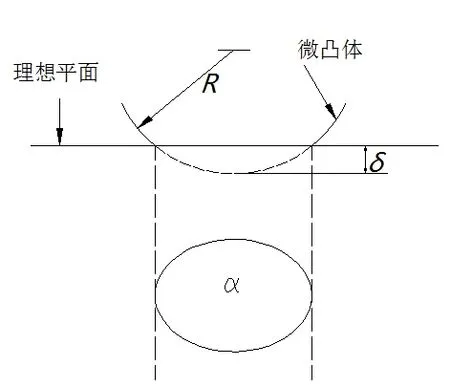
图1 微凸体接触模型

当单个微凸体与理想平面接触发生弹性变形时，其法向接触刚度可由式(1)表示。

当单个微凸体与理想平面接触发生弹性变形时，其切向接触刚度可由式(2)表示。

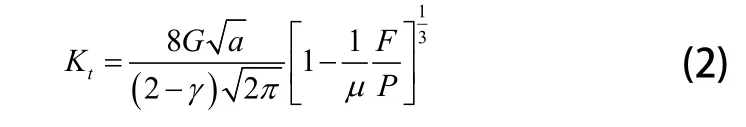
R为曲率半径（微凸体）；

δ为变形量（微凸体）；

E为弹性模量；

G为当量剪切弹性模型；

γ为泊松比；

µ为摩擦因数；

α为微凸体截面面积；

P为法向载荷（作用于微凸体）；

F为切向载荷（作用于微凸体）。

由上可知法向载荷、切向载荷、表面粗糙度、介质状况、结合面的材料及结构类型是影响法向、切向接触刚度的主要因素，法向、切向接触刚度是决定结合面间应力、应变、变形的主要因素，研究结合面间的法向载荷、切向载荷、表面粗糙度、平面度对螺栓结合面的影响是本课题的主要研究内容。

2 理论分析及仿真

2.1 建立模型

如图2所示试验装置材料选用HT300，螺栓选用直径为10mm性能等级为12.9的标准螺栓，其最大紧固螺距为116Nm，最大预紧力为45.2kN，实际预紧力不应超过最大预紧力的80%（仿真预紧力选用35kN），镶条选用紫铜，如图2所示是一种重型机床结构件装配应力测试试验平台，两个滑块分别安装于各自的水平导轨上，滑块与水平导轨的侧接触面之间存在镶条；两个立柱分别安装于各自的滑块上；两个后支架对称地安装在底座上，位于各自水平导轨的末端；两个电机通过各自的后支架固定在底座上；两个立柱均与平衡梁连接；活动横梁安装于立柱的竖直导轨上，活动横梁与竖直导轨的侧接触面之间存在镶条；两个竖直方向上的电机固定在平衡梁上，电机通过丝杠使滑块前后移动、横梁上下运动。

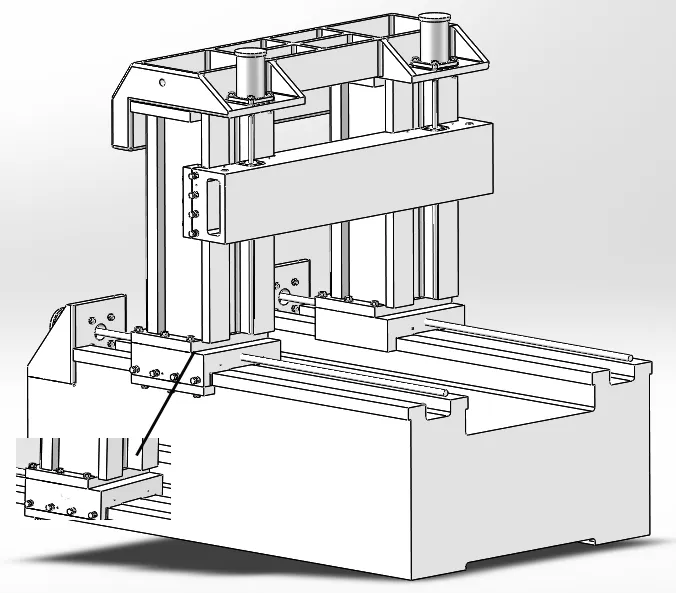
图2 重型龙门机床三维图

本课题研究立柱装配过程中产生的压力、扭矩对结合面应力变化的影响，同时也研究存在加工误差情况下，结合面应力随表面粗糙度、平面度误差的变化情况。

2.2 横梁自重变化引起的压力变化对结合面应力的影响

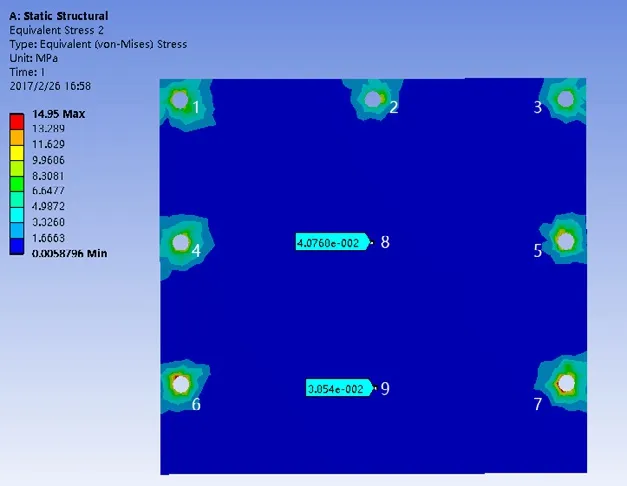
图3 初始状态滑块上表面应力分布图

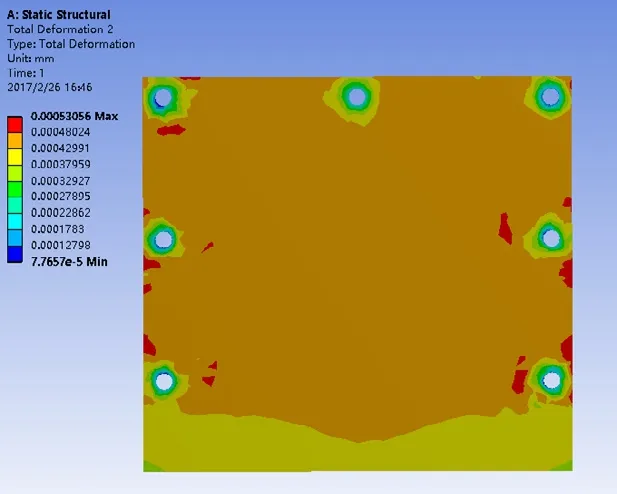
图4 初始状态滑块上表面变形分布图

图5 横梁自重引起的应力变化

如图5所示，当横梁加载G时，所产生的效果是作用在滑块表面的M1、M2之和。

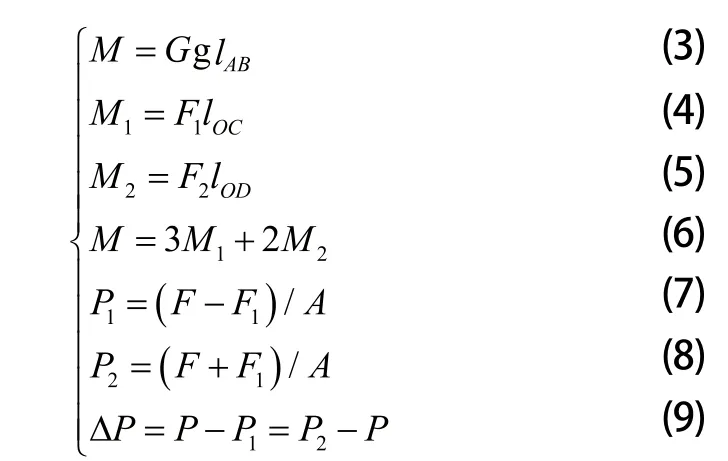
F为螺栓孔周围平均压力，F1、F2为横梁自重影响下螺栓孔周围平均压力的增大或减少量，F约为螺栓预紧力的1/10，机床尺寸、螺栓预紧力已知，当G=4000N时，求得∆P=0.66MPa。

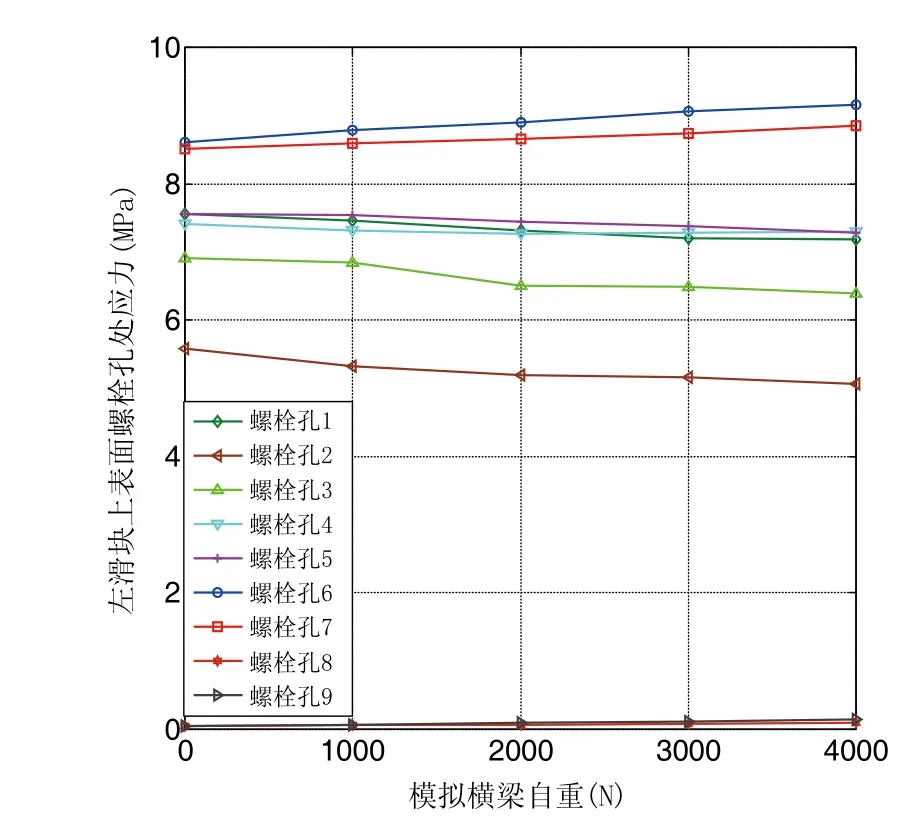
图6 螺栓孔应力随横梁自重变化情况

由仿真可知，应力变化范围在0.6MPa左右，和理论计算结果近似，初始状态滑块上表面变形分布较均匀（如图4所示），随着模拟载荷的不断增加，上表面底部变形出现越来越紧密的上下分层现象，所有螺栓孔处变形也逐渐变大，但最大变形只有几微米。加载前6、7螺栓孔处应力最大，达到9Mpa左右，而2处螺栓孔处应力最小，将近6Mpa左右，其他螺栓孔处应力差别不是很大（如图3所示），左滑块上表面1、2、3随着横梁自重增加，应力逐渐变小， 6、7孔处应力逐渐变大（如图6所示），4、5孔处应力基本不变，滑块上表面8、9俩点应力呈现微弱的变大，说明随着横梁自重的增加左右立柱向加载方向发生了倾覆。

2.3 立柱装配引起的扭矩变化对结合面应力的影响

立柱装配产生扭矩的作用效果为摩擦力矩和螺栓力矩之和。

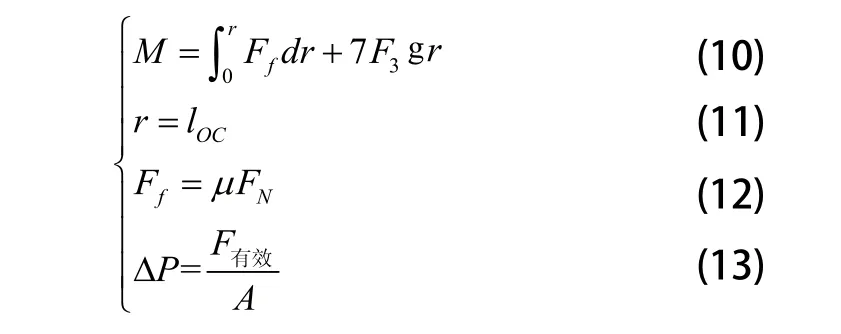
摩擦系数为0.1，F3为螺栓与螺栓孔的挤压力，F有效约为F3的1/10，当M=2000Ngm时，由式(11)～式(14)计算可知=0.38MPa。

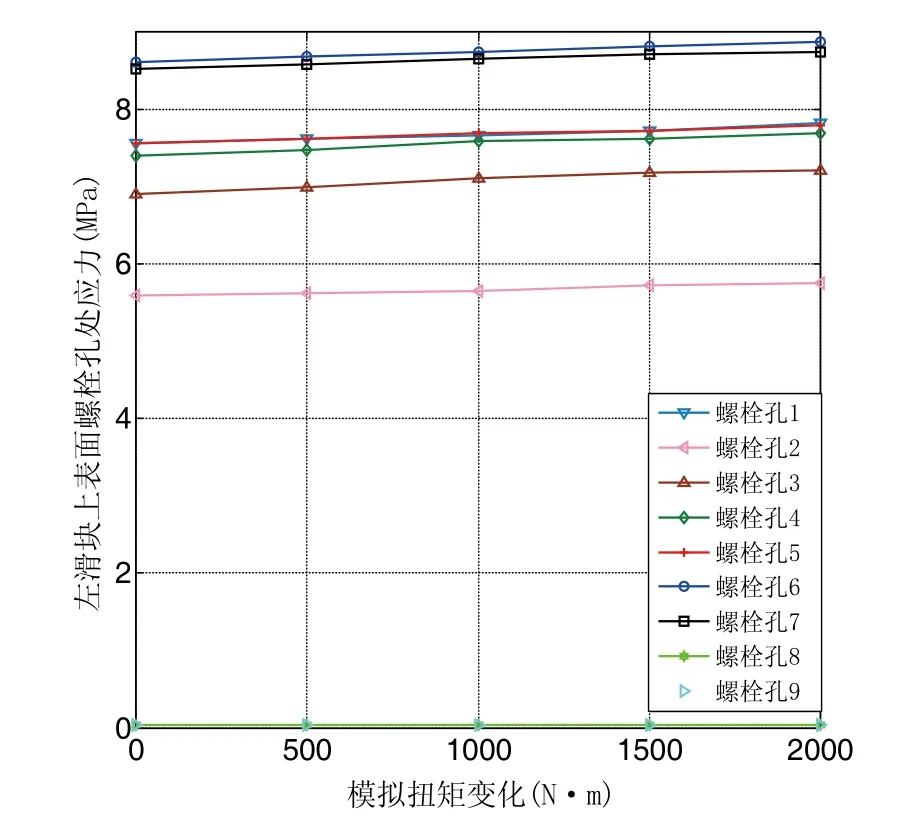
图7 螺栓孔应力随扭矩变化情况

由仿真可知，应力变化范围在0.3MPa左右，和理论计算结果近似，仿真中给立柱xy平面上逆时针的扭矩，初始状态滑块上表面变形分布较均匀，随着模拟扭矩的不断增加，左滑块表面螺栓孔处的变形不明显，螺栓1、2、3、4、5、6、7处应力随着模拟扭矩的增加都逐渐变大（如图7所示），滑块上表面8、9点应力的变化范围非常小，可以认为扭矩对8、9影响很小，由上可知，随着模拟扭矩的持续增加，螺栓与螺栓孔发生挤压，螺栓孔处的应力也随之变大，而扭矩的改变对于表面其他处的应力变化影响非常小。

2.4 结合面粗糙度对结合面应力的影响

研究表面粗糙度对结合面应力的影响，可以转化为摩擦系数对结合面的影响，摩擦系数和实际接触面积的关系如式(15)、式(16)所示。

图8 螺栓孔应力随摩擦系数的变化情况

0τ为剪切强度，其变化程度远大于，故A，成反比，当摩擦系数不断变大时，其实际接触面积会变小，压力不变的情况下其应力会变大。由于仿真不能直接加粗糙度，可以改变摩擦系数来模拟粗糙度的变化对结合面螺栓孔处应力的影响，初始状态滑块上表面变形分布较均匀，随着模拟摩擦系数的不断增加，左滑块表面螺栓孔处的变形非常明显，结合面螺栓孔处应力随着摩擦系数增大呈现近似线性趋势的变大，当摩擦系数从0.1变大到0.5时，应力变化最大达到5MPa，点8、9处应力也变大了将近1MPa左右（如图8所示），可以认为粗糙度对螺栓结合面上所有点的应力变化都有较大影响。

2.5 滑块上表面平面度公差对结合面应力的影响

图9 表面不平面示意图

滑块上表面存在如图9所示不平面的情况时，2处（滑块上表面上部中间处）螺栓变形最大，当t=200μm时， 2处螺栓变形、结合面应力如式(16)、式(17)所示。

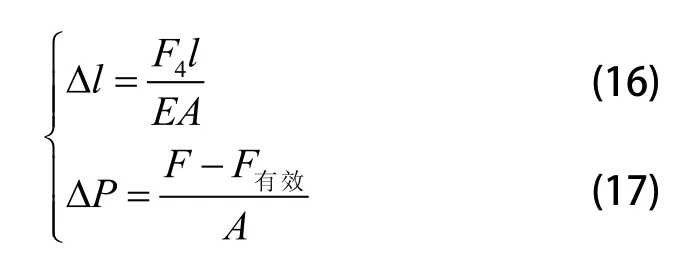
F4为螺栓预紧力，F有效为预紧后表面的压力，螺栓孔2处的应力变化由计算可求得∆P=3.5MPa。

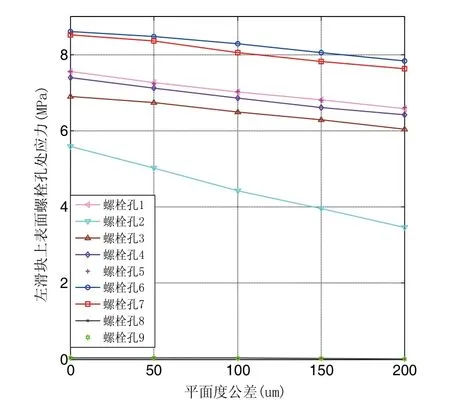
图10 螺栓孔应力随平面度公差的变化情况

由仿真可知，2处应力变化范围在3MPa左右，和理论计算结果近似，初始状态滑块上表面变形分布较均匀，模拟力加载前6、7螺栓孔处应力最大，而2处螺栓孔处应力最小，其他螺栓孔处应力差别不是很大，随着表面平面度公差的不断增加，左滑块上表面1、2、3、4、5、6、7应力都呈现逐渐变小的线性趋势， 2孔处应力变化最明显，滑块上表面8、9俩点应力呈现微弱的变小趋势（如图10所示），说明结合面平面度公差对螺栓结合面应力影响较大。

3 实验结果

试验是在横梁上加载重物来模拟横梁自重的变化情况，在螺栓孔外侧贴上应变片来记录各螺栓孔处的应力变化，由于1、2、3变化趋势相似，4、5变化趋势相似，6、7变化相似，可以取各组的平均值来反映上中下螺栓孔应力的变化趋势，仿真1为1、2、3应力平均值，仿真2为4、5应力平均值，仿真3为6、7应力平均值，实验与仿真结果如图11(a)所示。

由于应变片是贴在靠近螺栓孔处滑块外侧，与实验仿真结果存在误差，但其变化趋势基本一致，说明仿真与实验的一致性。

由仿真结果可知，随着摩擦系数的变大，螺栓孔处应力都有变大的趋势，可以取螺栓孔处应力的平均值来和实验结果比较，实验中通过贴塑来模拟表面的不同粗糙度，实验和仿真结果基本一致，结果如图11(b)所示。

由仿真结果可知，随着扭矩的变大，螺栓孔处应力都有变大的趋势，实验和仿真结果其变化基本一致，差值在1Mpa左右，结果如图11(c)所示。

由仿真结果可知，随着平面度公差的变大，螺栓孔处应力都有变小的趋势，取螺栓孔处应力的平均值作为仿真值，实验中通过铣表面来创造表面的不平面度，实验和仿真变化基本一致，结果如图11(d)所示。

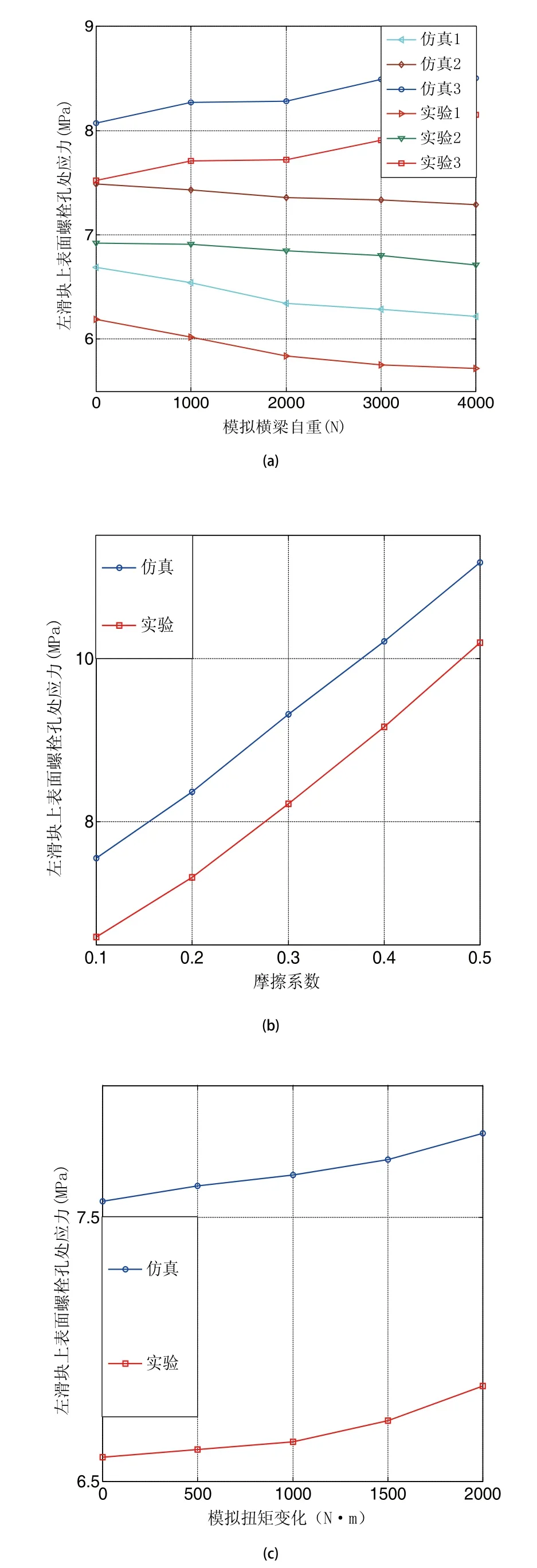
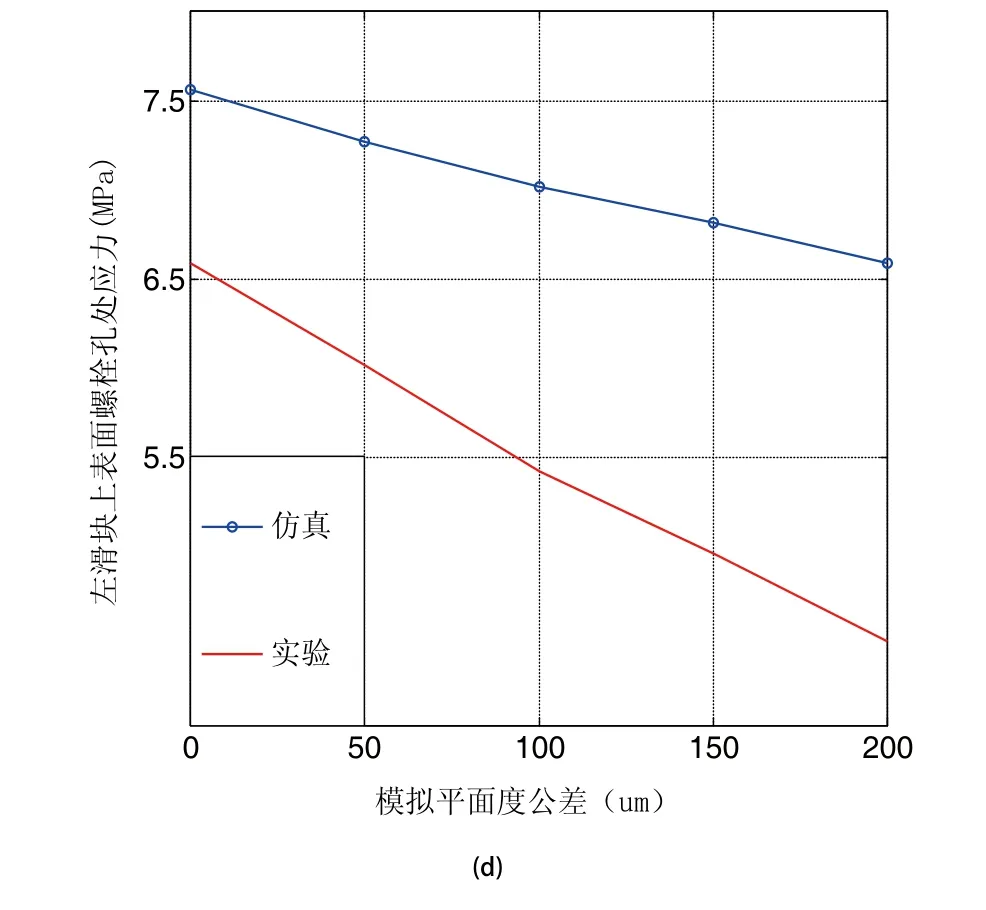
图11 在滑块上表面螺栓孔处应力变化情况

4 结束语

1）基于分形理论，本文所建立的结合面接触分形模型可以通过法向载荷（横梁自重）、切向载荷（扭矩）、表面粗糙度、表面平面度对螺栓结合面应力进行理论预估、仿真预算、实验验证。

2）法向载荷（横梁自重）对螺栓结合面的应力影响较明显，随着横梁自重的增加，立柱发生了倾斜，表面变形出现越来越紧密的分层现象，表面底部螺栓孔应力逐渐变大，表面上部螺栓孔应力逐渐变小。

3）切向载荷（扭矩）对螺栓结合面的应力也有影响，扭矩的增大对表面变形几乎没影响，但螺栓孔应力逐渐呈现微弱变大的趋势，说明螺栓与螺栓孔发生了挤压现象。

4）结合面表面粗糙度对螺栓结合面的应力影响很明显，随着粗糙度的变大，上表面变形、应力都逐渐变大，螺栓孔应力与粗糙度有较为明显的线性关系，螺栓孔处应力变化比表面其他处更为明显。

5）随着平面度公差的变大，螺栓结合面的应力都发生逐渐变小的趋势，螺栓孔应力与平面度公差有较为明显的线性关系，螺栓孔处应力变化比表面其他处更为明显。

6）理论、仿真、实验结果基本一致，说明了本文建立的理论模型和仿真模型的合理性和有效性。

[1] 张学良,温淑花.机械结合面静动态特性研究回顾与展望[J].太原重型机械学院学报,2002,23(3):276-281.

[2] 温淑花,张学良,武美先,等.结合面法向接触刚度分形模型建立与仿真[J].农业机械学报,2009,40(11):197-202.

[3] 温淑花,张学良,文晓光,等.结合面切向接触刚度分形模型及其仿真[J].农业机械学报,2009,40(12):223-227.

[4] 张学良,温淑花,兰国生,等.平面结合面切向接触阻尼分形模型及其仿真[J].西安交通大学报,2011,45(5):74-77,136.

[5] 尤晋闽,陈天宁.基于分形接触理论的结合面法向接触参数预估[J].上海交通大学学报,2011,45(9):1 275-1,280.

[6] 尤晋闽,陈天宁.结合面法向动态参数的分形模型[J].西安交通大学学报,2009,43(9):91-94.

[7] Majumdar A,Bhushan B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces[J].ASME Journal of Tribology,1990,112(2):205-216.

[8] Majumdar A,Bhushan B.Fractal model of elastic- plastic contact between rough surfaces[J].ASME Journal of Tribology,1991,113(1):1-11.

[9] Z.M.Levina.Calculation of Contact Deformations in Slideways[J].M achine and Tooling,l965,36(1):l-8.

[10] M.Masuko,Y.ITO and C.Fujinoto．Behaviour of Horizontal Stif fness and Micro-sliding on the Bolted Joint under the Nor-mal Pre-load[A].Pro c.12nd Intem.Confer.M.T.D.R[C].1972.

Study on the stress of column joint surface of heavy machine tool

CHEN Hao, QI Xiang-yang, SHI Kai, TIAN Shang- pei

TH115

：A

1009-0134(2017)07-0048-05

2017-05-06

“高档数控机床与基础制造装备”科技重大专项：重型机床可靠性试验与评价方法的研究（2014ZX04014011）

陈浩（1993 -），男，安徽六安人，硕士研究生，研究方向为机床结合面及装配精度保持。