汽车天窗密封条分析与优化
蒋振宇,陈忠钰
(伟巴斯特车顶系统中国有限公司研发中心,上海 201108)
汽车天窗密封条分析与优化
蒋振宇,陈忠钰
(伟巴斯特车顶系统中国有限公司研发中心,上海 201108)
全面阐述了天窗密封条设计的三大性能要求:装配性,刮擦性和密封性。在设计天窗密封条时,除了需要考虑密封条本身结构功能特性以外,更需要考虑产品的可制造性和可装配性。在考虑制造能力的前提下,列举了用有限元方法解决这三大性能问题的实际案例,并取得了良好的效果。
汽车天窗;密封条;结构优化;计算机辅助工程
0 引言
汽车天窗上有许多密封条,特别是全景天窗。天窗密封条主要是降低噪声,防止外部风沙、雨水、尘土等物质浸入车内。密封条在车顶中的位置如图1所示。在设计和测试天窗的时候,天窗密封条有三大难点:装配困难,刮擦噪声和漏雨或不隔音。作者将以有限元分析为基础,介绍某公司在2009年和2013年利用有限元技术对密封条进行装配、刮擦和密封仿真分析和优化的案例。

图1 某天窗前端Y-O截面视图
1 天窗密封条结构
天窗上有许多种密封条,比如:主密封条,隔音密封条。所有的天窗密封条都由下面两部分组成:
(1)密实橡胶。主要用以将密封条固定在车顶或天窗上,要求在装配时有较小的插入力和拔出时有较大的保持力,以满足密封条在汽车或天窗装配流水线上的装配方便性和可靠性。
(2)发泡橡胶。主要承受天窗关闭时的压缩载荷,以产生密封性和回弹性能,同时还可以弥补天窗与车顶开口之间的间隙不均匀。
2 橡胶材料本构模型
橡胶材料在大变形的情况下不满足胡克定律,即受力和变形或应力和应变是非线性关系。密实橡胶在变形中体积变化比较小,具有几乎不可以压缩的材料特性;发泡橡胶在变形中体积变化极大,具有可压缩的材料特性。在研究橡胶材料时,通常用应变能势函数来描述其力学行为,其中应用较多的应变能密度函数是Mooney-Rivlin和Ogden。
2.1 密实橡胶材料模型
2.1.1 Mooney-Rivlin橡胶材料模型
M MOONEY在1940年提出了应变能势函数[1]:
W=C1(I1-3)+C2(I2-3)
(1)
式中:C1和C2为与温度相关的材料常数,由试验确定;I1和I2分别是Cauchy-Gree变形张量的第一和第二不变量:
(2)
(3)
式中:λ1、λ2、λ3是主伸长比。
R S RIVLIN在1951年提出另外一种应变能函数[2]:
(4)
式中:Cmn是与温度相关的材料参数,m、n为从0开始的整数,其数值越大,拟合所得的应变能势函数精度就越高。式(1)、式(2)即为MOONEY-RIVLIN模型。式(1)因为简洁而应用比较多。
2.1.2 Ogden橡胶材料模型
1972年Ogden直接采用3个主伸长比作为应变能函数的自变量,提出了不同于Mooney-Rivlin模型的新应变能密度函数[3]:
(5)
式中:μn、αn是材料参数,由材料试验数据决定。此模型是目前准确性较高的不可压缩弹性体材料模型,因此本文采用此模型模拟密实橡胶。
2.2 发泡橡胶材料模型
1972年OGDEN同样直接采用主伸长作自变量,提出发泡橡胶材料模型[4]:
(6)
式中:λi(i=1,2,3)为主拉伸长比;μn、αn和βn(n=1,2,3)为材料常数,其值根据发泡橡胶材料的单轴拉伸、平面剪切和体积试验数据确定。该模型不仅能比较准确地反映发泡橡胶材料特性,还可适用于高度可压缩性材料,文中采用此模型来模拟发泡橡胶。
3 天窗密封条装配分析与优化
在天窗密封系统中,密封条的插拔力是评价密封条安装特性和可靠特性的一项重要指标。由于零件的制造和装配误差的存在,良好的插拔特性要求密封条在装配间隙最小的时候有较小插入力和在装配间隙最大的时候有较大的拔出力,防止在使用过程中脱落。
下面将以该公司某款天窗密封条为例,介绍天窗密封条装配性分析。具体密封条截面如图2所示,此密封条已经批量生产,经常听到生产部门的抱怨:密封条在最小装配间隙的时候十分难装,甚至有时候需要借助于榔头才能完成装配。如果密封条被较大的力强行压入玻璃总成,必定会对玻璃的弧度、表面张应力和安全性产生影响。
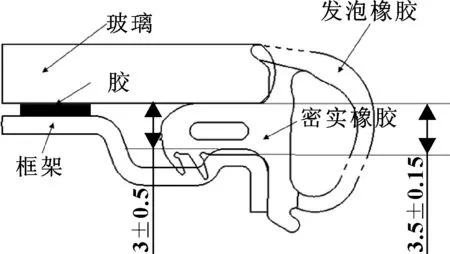
图2 某天窗密封条装配到玻璃总成后的截面图
从图2可知:影响密封条装配性的两个关键尺寸,分别是图2中标注的玻璃和框架之间的装配间隙尺寸和密封条密实橡胶的主体厚度尺寸。为了研究方便,把密度条主体厚度尺寸作为不变量,根据公差计算,玻璃和框架之间的最小间隙是2.35 mm。
为了解决装配困难的问题,进行了有限元分析,假设玻璃和框架是刚体,在装配间隙最小的时候,把密封条插入玻璃和框架之间。根据CAE结果,在t=0.57 s的时候密封条网格变形特别大,如图3所示,根本就压不进去,说明密封条十分难装。

图3 原始结构密封条在装配过程中的变形
为了解决在最小装配间隙下的安装问题和平衡在最大装配间隙下的拔出力和外观问题,考虑到粘胶玻璃总成的工艺水平,把玻璃和框架之间的间隙增大到3.8 mm,同时对密封条的截面进行了优化,如图4所示。
同样也对新的密封条进行了有限元分析,密封条能够在最小装配间隙下被顺利地插入,如图5所示;最大插入力101 N/100 mm,如图6所示,装配非常方便。

图4 天窗密封条优化示意

图5 优化后的密封条在装配过程中的变形

图6 新的密封条在装配过程中的插入力
除了上面完成的密封条在最小装配间隙下的插入分析,还进行了在最大装配间隙下的拔出和外观性分析,新的密封条拔出力和外观特性都符合生产和设计的要求。此密封条设计已经应用到产品中,在大批量生产的过程中再也没有听到任何抱
怨了。
4 天窗密封条刮擦分析与优化
天窗在打开和关闭的时候,密封条不断地刮擦车顶,常常产生各种噪声。下面将以该公司某款天窗密封条为例,模拟密封条在天窗打开和关闭过程中的变形情况。
此天窗在打开和起翘实际测试过程中,特别在密封条与车顶干涉量比较大的时候,经常听到“砰”的声音,这个问题一直困扰着设计和测试工程师。为了解决此问题,进行了密封条刮擦有限元分析,根据有限元分析结果,在t=1.0 s的时候,由于摩擦力的作用,密封条产生滞后运动,天窗继续打开;在t=1.4 s的时候,密封条突然释放如图7所示,根据经验判断,密封条必然会扰动空气,产生“砰”的声音。

图7 原始结构密封条在天窗打开过程中的变形图
影响密封条与车顶滑动的因素很多,如密封条的结构和表面涂层、车顶翻遍工艺和表面涂层等。根据此密封条具体结构及装配要求,把改变发泡橡胶的形状作为优化方案:增大泡管下面的壁厚,并将泡管向上移动。新的密封条结构如图8所示。
再次进行有限元分析,根据CAE结果,新的密封条在与车顶刮擦的过程中再也没有出现停滞状态,如图9所示,优化效果比较明显;在实际测试过程中,再也没有出现“砰”的声音。
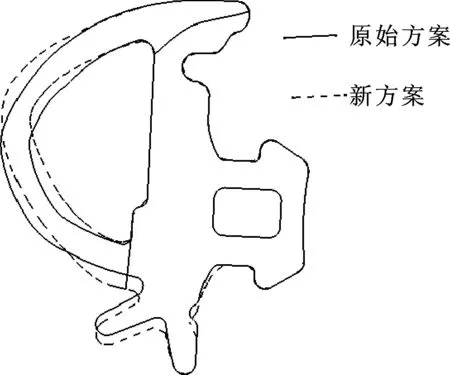
图8 天窗密封条结构优化示意

图9 新的密封条在天窗打开过程中的变形图
5 天窗密封条在拐角处密封性分析与优化
为了研究密封条在弯曲时的材料流动情况,可以借鉴板料弯曲网格实验来说明密封条在弯曲前后截面形状的变化,如图10所示。板料在弯曲前后,必有一层纤维材料的长度在弯曲前后保持不变,这一层材料层定义为应变中心层(见图10 中的o-o层),根据体积不变原则,当板料在弯曲变形的时候,外侧材料受拉伸长(网格长度b-b变长),材料在厚度方向会减薄,内侧材料受到压缩(网格长度a-a变短),材料在厚度方向会增厚[5]。由此可见,密封条在弯曲时,外侧材料在厚度方向必定减薄,与车顶的干涉量也必定会减少,内侧材料在厚度方向必定会增厚,容易引起起皱。

图10 板料弯曲前后坐标网格的变化
为了研究天窗拐角处密封条与车顶的密封情况,2009时该公司进行了相关研究。选取某一个天窗密封条为研究对象,进行了CAE分析,把密封条装到玻璃总成后,发现天窗拐角处的密封条与车顶的干涉量明显减少,如图11所示,这样容易引起天窗在车顶拐角处漏雨,CAE分析结果符合理论推理,验证了CAE分析的合理性。为了消除天窗拐角处的密封条与车顶干涉量减少的问题,对玻璃总成进行了补偿设计,然后同样进行了CAE分析,发现天窗拐角处的密封条与车顶的干涉量没有变小,如图12所示,说明玻璃总成的补偿设计是合理的。因此在设计天窗的时候,特别需要注意密封条在拐角处的密封情况,否则就会带来主密封条漏雨,隔音密封条不隔音和密封条起皱的问题。

图11 玻璃总成没有补偿设计时拐角密封条与车顶干涉量

图12 玻璃总成补偿设计后拐角密封条与车顶干涉量
其实,对于整个天窗的密封情况,还需要通过有限元仿真把整个天窗装到车顶上后,检查密封条与车顶之间的接触压强,判定天窗的密封性。
6 天窗密封条CAE其他研究
天窗密封条CAE其他研究包括:汽车天窗密封条动力学建模和隔音仿真分析;汽车天窗密封条截面拓扑和形状优化仿真分析;汽车天窗密封条起皱仿真分析。
7 结论
全面、系统地阐述了天窗密封条设计的三大性能要求:装配性、刮擦性和密封性,并列举了用有限元方法解决这三大性能问题的实际案例。
从上面的一些案例分析可知:在密封条前期开发阶段,必须借助专业的有限元软件对密封条的性能进行分析,避免产品的一些缺陷,从而能够减少试验次数,并降低产品的开发成本和缩短其开发周期。
[1]MOONEY M.A Theory of Large Elastic Deformation [J]. Journal of Applied Physics,1940(11):582.
[2]RIVLIN R S,SAUNDERS D W.Large Elastic Deformations of Isotropic Materials:Part 7:Experiments on the Deformations of rubber[J].Philosophical Transactions of Royal Society,1951,243:251-288.
[3]OGDEN R W.Large Deformation Isotropic Elasticity:On the Correlation of Theory and Experiment for Incompressible Rubberlike Solid[C]//Proceedings of the Royal Society,1972:565-584.
[4]李欢,李惠林,张斌,等.基于Msc.Marc的汽车车门密封条起皱分析及优化[J].橡胶工业,2015,62(3):169-171.
[5]邓仕珍,范淼海.汽车车身制造工艺学[M].北京:北京理工大学出版社,2004.
Vehicle Sunroof Seal Analysis and Optimization
JIANG Zhenyu,CHEN Zhongyu
(Research Center,Webasto Roof China Co., Ltd., Shanghai 201108, China)
Three property requirements for seal design of vehicle sunroof were disclosed, including assembly, scratch and sealing. When the seal was designed, not only its own structural features should be considered, but also the product manufacturability and assembly were needed to consider more. With the help of finite element software, some successful cases were chosen to explain three property requirements of seal design, and good results were obtained.
Vehicle sunroof; Seal; Structural optimization; CAE
2017-03-16
蒋振宇(1977—),男,硕士,高级工程师,研究方向为结构耐久、安全和NVH分析与优化等。E-mail:Michael.Jiang@webasto.com。
10.19466/j.cnki.1674-1986.2017.07.008
U467.2
A
1674-1986(2017)07-030-04

