股市风险溢价的非对称性研究——基于传媒行业指数的分位数回归分析

赵宸浩，李坤明，郑旗山，黄和亮

(福建农林大学经济学院，福建 福州350002)

股市风险溢价的非对称性研究
——基于传媒行业指数的分位数回归分析

赵宸浩，李坤明*，郑旗山，黄和亮

(福建农林大学经济学院，福建 福州350002)

运用分位数回归模型，以传媒行业为例，探究行业指数在不同市场行情下的风险溢价是否具有非对称性。研究结果表明：在传媒行业风险溢价较低时，其受大盘风险溢价影响较大；在传媒行业风险溢价较高时，其受大盘风险溢价影响有所减小；在传媒行业风险溢价极高时，其受大盘风险溢价的影响表现为剧烈的先增后减态势。基于以上实证结果，提出关于保护投资者利益、维护市场秩序的若干建议。

风险溢价；非对称性；分位数回归；传媒行业

我国证券市场从成立之时的8只股票，到如今2900多只股票，股票有效账户从1993年的835万多户，到2017年1月增加到11831万多户[1]。可见，我国股票市场不断发展，市场影响力不断扩大。在股市中，股票价格是人们关注的对象，其决定了投资收益的多少，而市场风险溢价是影响股票价格水平的关键因素。市场风险溢价是资本资产定价模型中重要的参数之一，通常是指股票资产与无风险资产之间的收益差。风险溢价的大小往往会对投资者的投资决策产生重大影响。影响个股收益的因素较多，且具有较大随机性，而从行业层面分析风险溢价具有平均效应，能够使分析结果具有更高的可信度和代表性。其中，选择A股指数和传媒行业指数为模型样本主要在于传媒行业指数的变动性较强，价格波动较大，而且包含的股票数量较多，有较大的资金容量，相对于其他行业指数具有更强的代表性，因此，本文以传媒行业指数作为研究对象来分析股市风险溢价的非对称性[2]。对风险溢价的研究有利于投资者理性选择投资组合及资产管理方案，有利于促进我国股票市场的良性发展[3]。

一、文献回顾

国内外学者针对股市风险溢价进行了大量的研究。Sharpe于1964年提出了著名的资本资产定价模型，描述了市场风险与资产风险溢价之间的关系[4]。程兵等利用几何平均模型、股利贴现模型和盈利增长模型分别计算A股的风险溢价，认为A股真实风险溢价为负，我国股票市场存在较大泡沫[5]。谢曙光采用定量分析的方法对我国股市投资收益非对称性问题进行实证分析，发现我国股市非流通股股东与流通股股东之间存在投资收益非对称性[6]。罗登跃等研究发现，股市的流动性风险溢价主要来源于市场收益与非流动性风险溢价的互相敏感性[7]。李小为从我国股票市场投资者的基本构成、市场有效性、心理特点以及羊群效应等方面分析了我国股票市场波动非对称性产生的原因，发现我国股票市场存在“尖峰厚尾”的特点[8]。邓可斌等在其研究的2个股市期间均没有发现风险溢价的证据，这一发现与国内大多数研究结果不同[9]。何兴强等在广义误差分布条件下，通过构建ANST-GARCH(M)-GED模型考察了不同市场态势下股票市场的非对称性反应，发现牛市、熊市态势下股市收益均具有非对称均值回归特征，但回归方式差异明显[10]。谭治国等采用分位数回归模型对股票风险值进行了有效估计，认为分位数回归模型在经济学研究领域中具有现实的可操作性[11]。佟孟华等认为系统流动性风险溢价具有不稳定性，在每个时期的表现均不一样[12]。王茵田等对我国股市风险溢价的截面差异进行研究，通过采用Fama-MacBeth两步回归法，发现债市的指标能够显著影响股市风险溢价，同时资产定价理论中的投资比率和现金流股价比能够反映我国股市风险溢价[13]。黄芬红等认为利好消息和利空消息对特质波动的影响存在非对称性[14]。

关于我国股市的研究主要集中在宏观层面上，研究政策对股市的影响，关于股市风险溢价方面的研究则较少。已有研究也主要关注我国股市整体的风险溢价并与外国股市进行对比，而对我国股市内部及各板块的风险溢价特征研究较为缺乏。众多研究表明，行业因素对投资者的投资决策影响越来越大，股票行业收益的波动性将直接影响投资者尤其是机构投资者的资产配置状况[3]。因此，本文选取传媒行业的数据进行分析，同时针对股市收益率“尖峰厚尾”的特征，采用分位数回归模型进行分析，以此探究某个行业在不同市场行情下，受大盘的影响是否存在非对称性特征。

二、研究设计

Koenker等于1978年提出了分位数回归思想[15]。与最小二乘法相比较，分位数回归并非只针对一个分位点进行分析，而是对于不同的分位点进行分析，用几个分位函数来估计整体模型，从而可以使数据分析更加全面。传统的均值回归模型是关于因变量条件期望的回归，只能够分析自变量对因变量条件期望的影响，无法考察因变量条件分布在其他位置的信息。而分位数回归在进行回归分析时无需对序列的分布作出假设，因而就整体而言，分位数回归的方法更为稳妥。本文不仅要研究行业板块指数条件期望的信息，还要考察其在不同分位点的信息，因为在不同分位点下自变量系数的估计量常常不同，即自变量对不同水平因变量的影响不同。

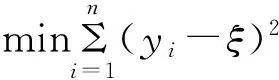
其中，ρτ(z)=τzI(0,∞)(z)-(1-τ)zI(-∞,0)(z)，函数I为示性函数。对于一般线性条件均值函数E(Y/X=x)=x′β，通过求解β=argminβ得到参数估计值。而一般线性条件分位数函数为Q(τ|X=x)=x′β(τ)，通过求解β(τ)=argminβ得到参数估计值。对于任意的τ(0,1)，β(τ)称为第τ回归分位位数[16]。

(二)分析与模型设定

1.样本数据。选择A股指数的日收盘指数、传媒板块指数的日收盘指数，以及上海银行间同业拆放利率的隔夜年利率数据为样本数据。传媒行业指数包含了沪深两市所有上市的传媒企业，本文选取以沪深两市中所有上市的传媒企业为基础编制的传媒行业指数，以及沪深两市上市的A股股票为基础编制的A股指数，所有样本取自2007年8月1日至2016年4月11日。经过两轮大牛市之后，样本数据跨越的时间维度较长、数据容量较大，数据代表性较强。剔除个别数据缺失的样本，总计样本量为2112个，数据来源于同花顺金融证券数据库及上海银行间同业拆放利率官方网站。

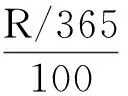
3.数据的描述性统计与单位根检验。通过收集整理传媒行业板块指数、A股指数及无风险利率，计算得出传媒板块风险溢价Cr和股市大盘风险溢价Crm的相关数据，各变量的描述性统计见表1。

在解答问题时，列出正确的函数关系式尤其重要。同时学生可能使用的数学知识通常为几何图形面积公式、勾股定理以及相似三角形等，应在实际问题解答期间结合各种数学知识背景对问题进行解答。如用勾股定理对函数表达式进行求解时，图中一定存在直角三角形或通过添辅助线，可以形成直角三角形。在使用相似三角形知识时，问题中通常具有平行线段以及角度相同的角。通常情况下很少直接有利用图形面积公式对函数关系式进行明确，通常需要结合实际需求进行相应的割补。

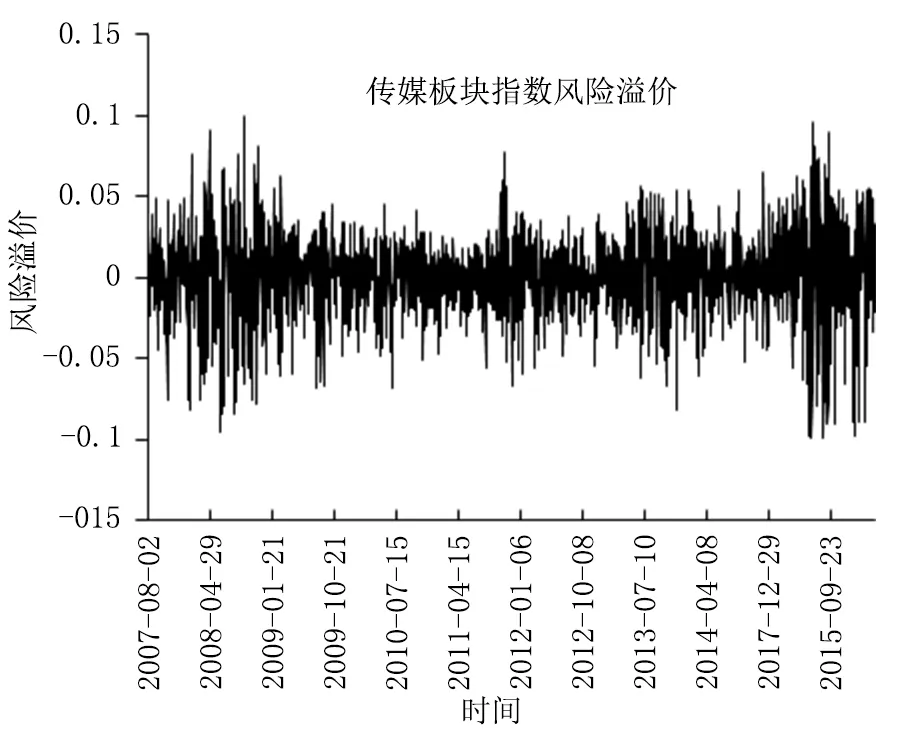
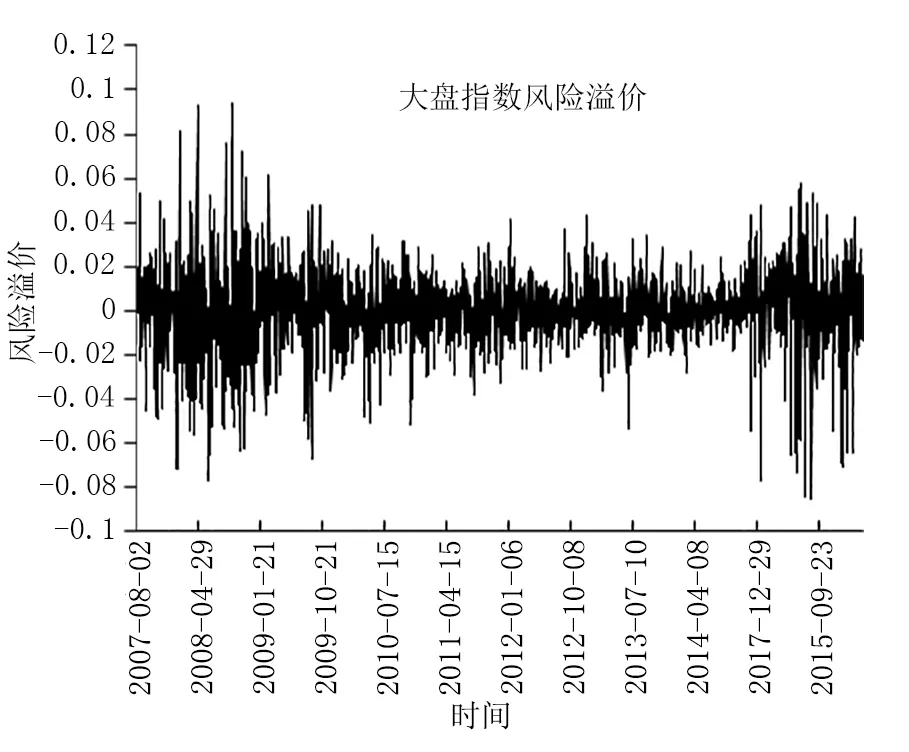
图1 股市大盘与传媒板块风险溢价对比图

从表1可以看出，rm、r、Crm、Cr这4个变量的标准偏差都大于其平均值，表明数据很有可能存在极端异常值，这说明仅依靠均值回归模型不能完整分析这些数据，故采用分位数回归模型进行分析。为了避免伪回归，确保估计结果的有效性，需要对Cr与Crm进行ADF单位根检验。经过检验，认为这2个变量都是平稳的(表2)。

表2 单位根检验结果

4.模型设定。资本资产定价模型认为，一项投资所要求的必要报酬率取决于以下3个因素：(1)无风险报酬率，即将国债投资(或银行存款)视为无风险投资；(2)市场平均报酬率，即整个市场的平均报酬率，如果一项投资所承担的风险与市场平均风险程度相同，该项报酬率与整个市场平均报酬率相同；(3)投资组合的系统风险系数，即β系数，是某一投资组合的风险程度与市场证券组合的风险程度之比。资本资产定价模型说明了单个证券投资组合的期望收益率与相对风险程度间的关系，即任何资产的期望报酬一定等于无风险利率加上一个风险调整后相对于整个市场组合的风险[17]。

资本资产定价模型的数学表述如下：

r=rf+(rm-rf)β+ξ

为了考察股市风险溢价的非对称性，本文以资本资产定价模型为基础，通过构建均值回归模型及分位数回归模型来估计平均意义上的风险溢价和在不同行情条件下的风险溢价，具体如下所示：

均值回归模型：r-rf=α+(rm-rf)β+ξ

分位数回归模型：Qr-rf(τ/rm-rf)=ατ+βτ(rm-rf)

其中，r-rf为因变量，表示传媒行业板块的风险溢价；Qr-rf(τ/rm-rf)为因变量，表示风险溢价分位数，rm-rf为自变量，表示A股风险溢价，τ[0,1]，表示分位数(分别取 1 %,5 %,…,95 %,99 %)。

5.模型参数估计。均值回归模型的估计结果见表3。从表3可以看出，Cm的系数估计值为1.0717910，并且该系数T检验的P值小于1%，说明在1%的显著性水平上显著，具有很强的正效应，就平均来看，A股风险溢价每增加一个单位，传媒板块风险溢价则相应增加1.0717910个单位。

利用传统的均值回归进行分析，只能得到条件分布期望值的信息(表3)。如果分布是对称的，也就是相当于中位数的回归，无法得到分布的其他位置的信息。为了检验在不同行情下风险溢价非对称性的存在，本文运用分位数回归方法，以大盘风险溢价为自变量，估计每一分位点上风险溢价的影响，也就是估计上述分位数回归模型。重要分位点的估计结果见表4。

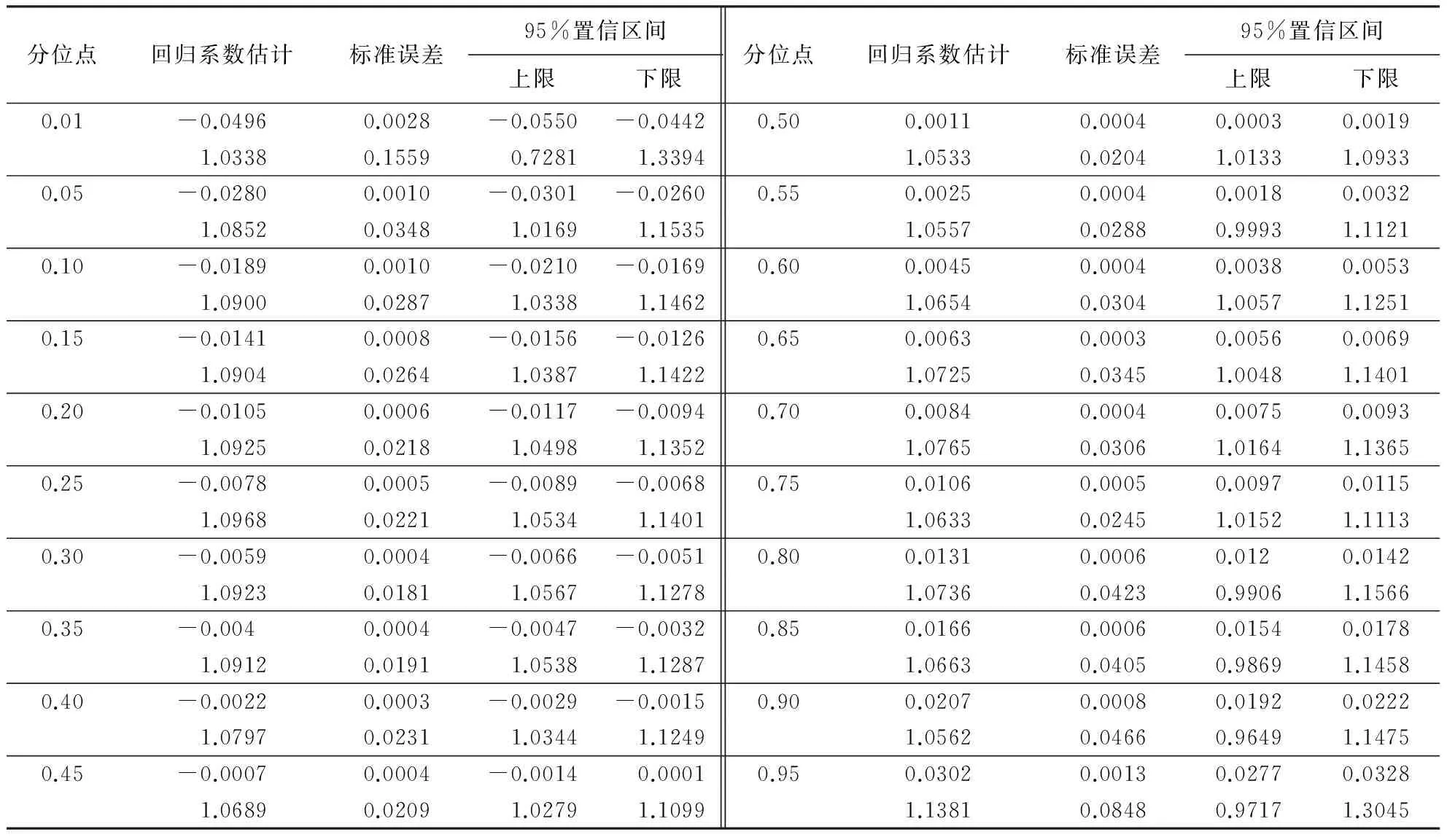
表4 分位数模型的系数估计结果

我国股市指数变化在不同时间段波动较大，股市风险溢价离散程度较高，因此，表4中列出了20个分位点，这样使信息不至于缺失，保证了信息的完整性。从表4可以看出，回归系数βτ的估计值均在置信区间内，说明βτ对风险溢价的影响是显著的。

三、模型估计结果的分析

当前，我国股票市场中个人投资者数量占据比例较高，股票市场的波动幅度较为剧烈，常常表现为暴涨暴跌，从2008年和2015年的2次股市异动中可以明显看出，大盘指数的风险溢价与行业板块的风险溢价呈现非对称性。一方面，由于存在信息的非对称性，个人投资者在获取信息方面的能力较弱，更依赖于公开的信息载体和传播媒介，而大盘指数作为股市信息的综合表现，在一定程度上能够给个人投资者提供参考意义，因此，行业的指数波动经常跟随大盘指数的波动，但在不同行情阶段，投资者对大盘的参考程度有差异。在较为低迷时期，个人投资者参与积极性不高，多为跟随大盘操作，此时的行业风险溢价与大盘风险溢价关联性较高；在行情较为高涨时期，投资者情绪高涨，参与积极性高，操作上不一定跟随大盘走势而采取更为激进方式，此时行业的风险溢价与大盘的风险溢价相关性降低。另一方面，个人投资者存在“羊群效应”，即个人投资者会根据其他投资者的行为而选择自己的投资行为，如在行情低迷时期，参与程度低，而在行情高涨时期，参与积极性大幅提高，进一步加大了行业风险溢价与大盘风险溢价的非对称性。

将表4中回归系数βτ的估计值和截距项的估计值整理制作成折线图(图2)。从图2中的右图可以看出，估计值的纵坐标基本上在1的上方，可见βτ的估计值几乎都大于1，可以判断传媒板块指数风险溢价与大盘指数风险溢价具有很强的相关性，但系数的估计值并不平稳，体现了传媒板块风险溢价受大盘风险溢价的影响程度不尽相同，显示了其非对称性质。

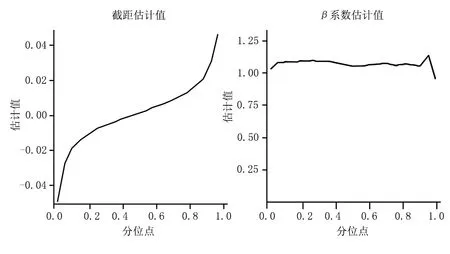
图2 分位数回归参数-分位点图

根据分位数回归模型的特点，可以看出分位数回归模型的分位点代表因变量的分布位置，而根据本文的研究内容，即收益率的分布位置，低分位点代表低收益率，高分位点代表高收益率。结合我国股市的特点，在行情较为低迷时期，股市收益率较低，在行情较为高涨时期，股市收益率较高，因此可以推测，在低分位点对应股市的熊市，在高分位点对应股市的牛市。

从表4可以看出，在0.01分位点至0.25分位点，回归系数β的估计值呈增加趋势，表明在低分位点时，传媒行业风险溢价受大盘风险溢价的影响逐渐增大，可能是因为在分位数较低的区间内，股票市场的行情为熊市，在熊市中大盘表现低迷，而传媒企业在熊市时对大盘的解读和信息的传播一般会给投资者造成消极影响，导致多数投资者参与积极性降低，以目前手中持有股票为基础减少操作，甚至不进行操作，持有股票也表现为跟随大盘的波动而变动，因此大盘低迷行情影响了传媒企业的表现，使得在这个分布区间内传媒行业风险溢价较低，故在此时传媒板块的风险溢价与大盘风险溢价相关性高，且受其影响较大。

在0.25分位点至0.5分位点，回归系数β的估计值呈下降趋势；在0.50分位点至0.70分位点，回归系数β的估计值虽呈上升趋势但幅度不大；在0.70分位点至0.90分位点，回归系数β的估计值先降后升然后又降，但每次幅度都较小。从总体来看，在0.25分位点至0.90分位点，回归系数β的估计值整体呈现下降趋势，表明传媒行业风险溢价受大盘风险溢价影响有所减缓，这种现象可能是由于大盘行情开始趋于稳定，呈现出由熊市转牛市的过渡行情，在此期间，传媒企业在察觉到行情扭转的趋势后，会对市场的表现及时作出反应，不再表现为跟随大盘的波动而变化，因此，传媒板块风险溢价受大盘风险溢价的影响逐渐减小。

在0.90分位点至0.99分位点，回归系数β的估计值呈现出先急剧上升后急速下降的趋势。此时大盘的波动较为剧烈，再加上当前传媒板块风险溢价处于高分位区间，板块收益率较高，可以推测市场进入大牛市阶段。传媒行业由于行业特点，对信息的获取能力和解读能力比其他企业稍强，当市场进入牛市预期时，最先反应的是传媒行业，而上市传媒企业作为受益者之一，股票自然而然也受到投资者关注，因此，其股价的涨幅较大，波动幅度甚至会超过大盘波动幅度，此时表现为传媒板块风险溢价受大盘风险溢价的影响急速增大。但当这种高位状态保持一定时间后，由于涨幅过大，投资者会担心大盘和个股的风险问题，而且我国股市在牛市期间，一直存在板块轮动效应，作为率先启动的传媒行业板块在经历了一定幅度的增长之后，自然而然地让位于其他涨幅较小的板块补涨，此时表现为传媒板块风险溢价受大盘风险溢价的影响急剧下降。

四、结论与政策建议

(一)结论

本文利用分位数回归模型实证检验了传媒行业股票指数风险溢价的非对称性，结论如下：(1)在低分位点时，传媒板块指数风险溢价与大盘指数风险溢价有较强的相关性，表明此时受大盘熊市影响较为突出。(2)在中间分位点时，两者的相关性有所降低，表明在该分位区间内，大盘行情开始趋于稳定，传媒板块指数风险溢价受大盘指数风险溢价影响逐渐减小。(3)在高分位点时，回归系数的估计值表现出较为极端的走势，剧烈地先升后降，表明传媒板块开始时受大盘行情影响很大，随后这种影响急剧下降。随着牛市的到来，大盘指数对传媒板块的影响先增后减，此时大盘处于一个比较高的位置，同时传媒行业的风险溢价也达到最大。

(二)政策建议

1．完善股票市场信息渠道建设。股票市场风险溢价的非对称性是信息非对称性的一种体现，个人投资者获取信息的渠道单一，导致信息传播不及时、不准确，从而对个人投资者的投资决策产生一定误导，引发市场剧烈波动。为了避免较大的市场风险和波动幅度，引导投资者理性投资，监管机构应加强股票市场信息渠道的建设，充分利用当下大数据、云计算等新型互联网信息技术，保障信息传播的及时性和准确性。

2．规范上市公司的信息披露制度。股票市场信息不对称的另外一种表现在于上市公司的信息披露不充分，股票价格往往是投资者依据已获得的股票信息并通过集合竞价与连续竞价形成。上市公司信息披露的充分性是促进市场形成合理价格、维护广大个人投资者利益的重要手段。我国监管部门应完善相关的法律法规，规范上市公司的信息披露，以保证信息的完整性。

3．加大对证券中介机构的监管。证券中介机构作为专业化程度较高的服务机构，能够为个人投资者提供比较合理的投资建议，因此受到越来越多的个人投资者的青睐。相关监管部门要加大对证券中介机构的监管，使其能更好地为中小投资者服务。

4．严厉处罚股票市场违法交易行为。“公开、公平、公正”是证券市场监管的3个基本原则，股票价格操纵与内幕交易等行为无疑违反了上述原则。这些行为使得股价不能反映股票的真实价值，不利于投资者进行投资判断，危害了投资者的利益，一定程度上扰乱了正常的市场交易秩序。监管部门应制定严格的法律法规，对上述行为进行严厉处罚，保证我国股票市场的平稳运行。

[1]中国证券登记结算有限责任公司.中国股票账户统计表[EB/OL]. [2017-01-06]. http://data.eastmoney.com/cjsj/yzgptjnew.html.

[2]方丽婷,李坤明.上证行业指数收益率的影响因素——基于三因素模型的分位数回归分析[J].金融理论与实践,2012(10):8-9.

[3]郭沛.我国股票市场行业指数波动非对称性与持续性的计量检验[D].长春:吉林大学,2011.

[4]SHARPE W F. Capital asset prices: a theory of market equilibrium under conditions of risk[J]. The Journal of Finance,1964,19(3):425-442.

[5]程兵,张晓军.中国股票市场的风险溢价[J].中国科学院,2004(2):23-26.

[6]谢曙光.中国股市投资收益非对称及其治理研究[D].上海:复旦大学,2003.

[7]罗登跃,王春峰,房振明,等.基于时间序列的上海股市系统风险流动性风险溢价实证研究[J].系统工程,2005,23(7):49-54.

[8]李小为.我国股票市场波动非对称性的实证研究[D].长沙:中南大学,2006.

[9]邓可斌,唐珺.股权规模、风险溢价与投资者理性——基于中国股市的经验研究[J].当代财经,2006(2):32-37.

[10]何兴强,李涛.不同市场态势下股票市场的非对称反应——基于中国上证股市的实证分析[J].金融研究,2007(8):131-139.

[11]谭治国,蔡乙萍.分位数回归在风险管理中的应用[J].统计与决策,2006(17):23-24.

[12]佟孟华,余世奎,HAN S.股市系统流动性风险溢价动态实证研究[J].财经问题研究,2010(1):58-63.

[13]王茵田,朱英姿.中国股票市场风险溢价研究[J].金融研究,2011(7):152-166.

[14]黄芬红,王志强.中国股市价值溢价与时变特质风险：基于GJR-GARCH-M模型的分析[J].金融经济学研究,2015,30(2):40-50.

[15]KOENKER R, BASSETT G. Regression quantiles[J]. Econometrica,1978,46(1):33-50.

[16]陈建宝.分位数回归技术综述[J].统计与信息论坛,2008(3):89-96.

[17]赵佳妮.浅谈CAPM模型中β的作用与局限性[J].学理论,2012(20):141-142.

(责任编辑： 何晓丽)

Asymmetry of stock market risk premium— Based on the quantile regression analysis of the media industry index

ZHAO Chen-hao, LI Kun-ming*, ZHENG Qi-shan, HUANG He-liang

(CollegeofEconomics,FujianAgricultureandForestryUniversity,Fuzhou,Fujian350002,China)

This article uses quantile regression model and takes the media industry as an example, explores whether the risk premium of the industry index in different markets is not symmetrical. The results show that when the risk premium is low in the media industry, it is affected by the broader market risk premium. When the risk premium is higher, its impact on the broader market risk premium has been reduced to some extent. But when the media industry risk premium is high, and its impact by the broader market risk premium shows a sharp increase in the trend after the decrease. Based on the above empirical results, this paper puts forward some suggestions on protecting the interests of investors and maintaining the market in order.

risk premium; asymmetry; quantile regression； media industry

2017-03-05

国家社会科学基金项目 (16BTJ018)；福建省中青年教师教育科研项目(JAS150251)。

赵宸浩(1992-)，男，硕士研究生。研究方向：金融计量与金融产品定价。*为通信作者。

F830.91

A

1671-6922(2017)04-0072-06

10.13322/j.cnki.fjsk.2017.04.012