基于MATLAB的二孩政策下人口增长模型研究——以郑州市人口为例

田海丽

(郑州工商学院 机械与电信工程学院，河南 郑州451400)

基于MATLAB的二孩政策下人口增长模型研究
——以郑州市人口为例

田海丽

(郑州工商学院 机械与电信工程学院，河南 郑州451400)

综合考虑影响二孩的各种因素，以郑州市历年人口数据为基础，给出二孩政策下人口增长模型函数——改进的Logistic模型，并采用MATLAB进行参数预测和函数建模；在建模过程中着重分析影响MATLAB建模性能优劣的两个关键因素：初值的设定和曲线拟合的实现方式；用MATLAB仿真软件，尝试多种Logistic曲线拟合的方法，找出性能良好的Logistic函数实现方法，最终确定二孩政策下的郑州人口增长模型；对多种方法设置不同的初始值来检验拟合方法对初始值的宽容度，最终找出对初始值宽容度较高的两种MATLAB，实现Logistic曲线拟合的方法：nlinfit非线性拟合和lsqcurvefit最小二乘拟合.

二孩人口增长模型；MATLAB；Logic回归模型；初始值设置；曲线拟合方法

0 引言

全面二孩政策放开以后，人口增加会对社会各方面带来影响，人口增长模型研究迫在眉睫，根据郑州市统计局公布的历年人口数，选取1980—2015年郑州市人口数据(表1)[1]进行人口增长建模，并用MATLAB 2016a软件仿真实现.得到性能较好的人口增长模型，较为准确地预测人口增长，进而为社会的各项活动顺利开展提供人口数参考.

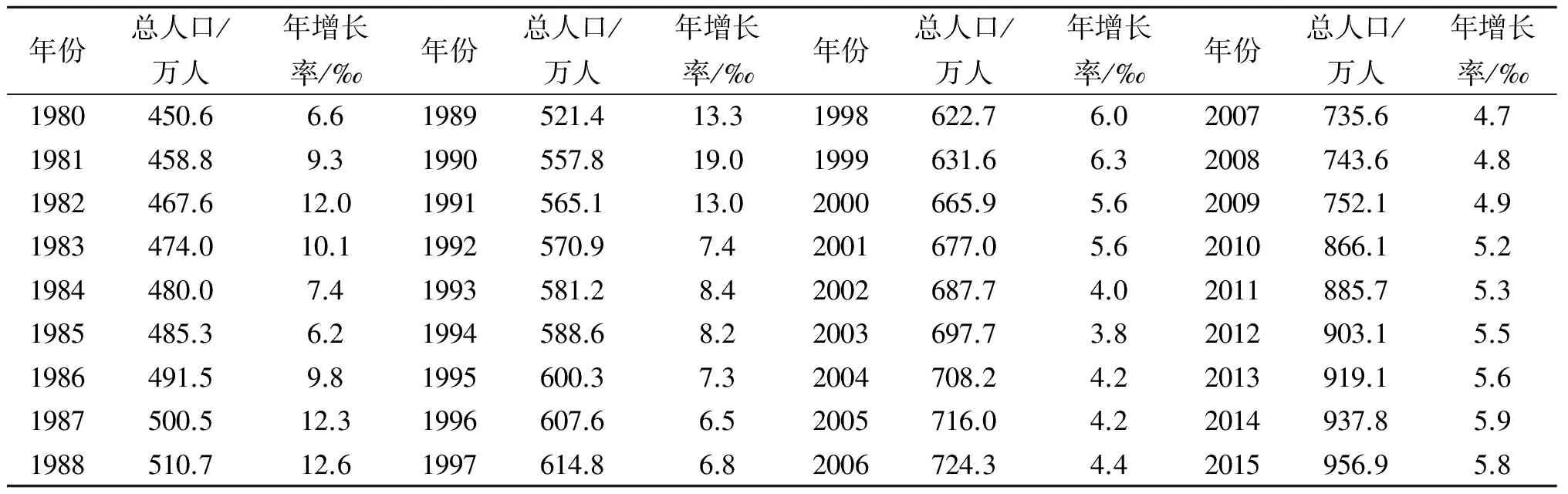
表1 郑州历年人口数Tab.1 The population of Zhengzhou in these years

1 相关理论和方法

1.1 Logic回归模型[2]

荷兰生物数学家提出Logistic人口增长模型为

(1)

其中，xm为自然资源和环境条件所能容许的最大人口，r为净相对增长率(出生率减去死亡率)，x(t)为第t年的人口数，x0为初始人口数.

考虑到影响二孩生育的因素，如夫妻年龄、夫妻职业、家庭收入、生育意愿、一孩性别、所在地区等，对Logistic人口增长模型进行改进,得到

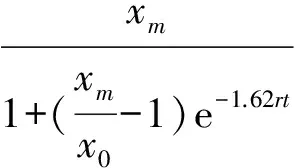
(2)

模型的关键是xm和r值的确定.

1.2 非线性回归的MATLAB实现

1.2.1 MATLAB提供的函数实现非线性回归

1)nlinfit函数[3],用于计算回归系数，可以得出拟合的回归系数和预测值.

2)lsqcurvefit函数[3],实现非线性最小二乘拟合[3]，命令格式为：[x,resnorm,res]=lsqcurvefit(@f,x0,t,y,lb,ub),f可以是M-函数或inline函数，x0=参数初值；t=自变量向量； y=函数值向量；lb,ub=参数的上下界；输出 x=参数估计值；resnom=(误差平方和)；res=r(误差向量).

3)lsqnonlin函数[4],实现非线性最小二乘拟合,命令格式为x=lsqnonlin(fun，x0，lb,ub)：lb与ub为变量x的下界及上界.lsqnonlin函数采用的是迭代法，由于程序的局限性，不可能搜索无穷大的区间，因此初始值的选择很重要.如果最优解离所给初始值比较近，迭代出该最优解的概率就很高.lsqnonlin指令适合求解任意形式的非线性拟合，需要先定义拟合函数，任取初始向量，调用lsqnonlin命令即可求得最优值.

1.2.2 MATLAB自定义非线性回归函数

MATLAB可以用3种方式来自定义函数：①命令inline;②用 “.m”文件；③用匿名函数定义要拟合的函数.

1.2.3 非线性回归曲线拟合相关方法和关键

1)初值的设定.非线性回归通常的求解方法具有局部收敛性，需要给出合适的初值，从生态学角度考虑，初始种群大小对于种群增长非常重要，初值准确与否是整个求解工作成败的关键[2,5-6]，因此需要找出对初值容忍度较大的实现方法.

2)曲线拟合实现方法.①非线性拟合模型线性化,常用的有取变量的倒数、对数，关系式的微分-积分线性化变化，分段线性化，将非线性拟合问题转化为线性拟合问题[5]，线性化拟合函数常用的有polyfit函数和regress线性回归函数.②直接非线性化拟合,常用的有nlinfit拟合、lsqcurvefit函数拟合、lsqnonlin函数拟合.

1.3 曲线拟合度的评判准则

决定系数R2，也称为拟合优度，R2越接近于1越好，越接近1表示拟合度越好，R2的公式为

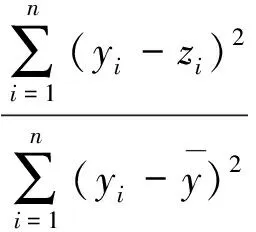
2 MATLAB曲线拟合实现

2.1 非线性直接拟合

1)取倒数，用nlinfit函数进行非线性拟合

实现程序如下，本次程序完整可运行，后面只给出程序核心部分.

>> t=0:1:35;

x=[450.6 458.8 467.6 474.0 480.0 485.3 491.5 500.5 510.7 521.4 557.8 565.1 570.9 581.2 588.6 600.3 607.6 614.8 622.7 631.6 665.9 677.0 687.7 697.7 708.2 716.0 724.3 735.6 743.6 752.1 866.1 885.7 903.1 919.1 937.8 956.9];

y=1./x; %取倒数

fy=inline(′a(1)+(1/450.6-a(1))*exp(-1.62*a(2)*t)′,′a′,′t′) %定义拟合函数

a=nlinfit(t,y,fy,[200,0.7]) %进行非线性拟合

t1=min(t):0.1:max(t);

y1=a(1)+(1/450.6-a(1))*exp(-1.62*a(2)*t1);

y2=1./y1; %还原

xm=1/a(1)

r=a(2)

y3=fy(a,t);

y4=1./y3;

R2=1-sum((y-y3).^2)/sum((y-mean(y)).^2) %决定系数

plot(t,x,′*′,t,y4,′o′,t1,y2)

>> title(′Logistic拟合曲线′)

>> legend(′Data′,′Logistic Fit′)

此时，决定系数为R2=0.989 1，接近于1，拟合优度较高，人口模型函数为

(3)

这种方法在确定a=nlinfit(t,y,fy,[-1,1])时，对初始值取值的宽容度较大，具体数据见图1，拟合结果见表2.

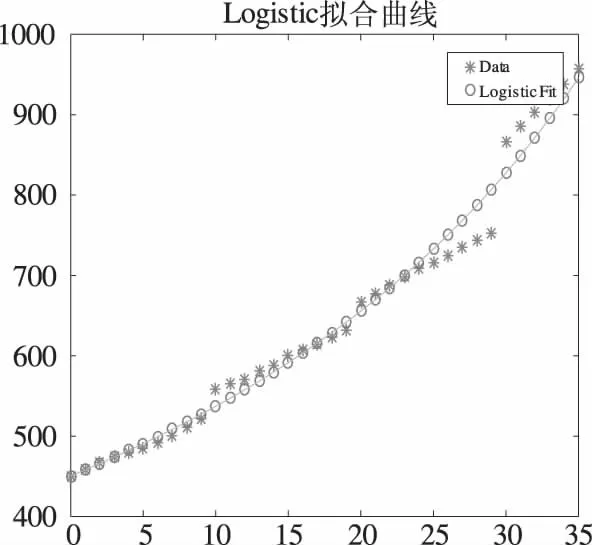
图1 nlinfit函数进行非线性拟合Fig.1 The performance of nlinfit nonlinear fitting

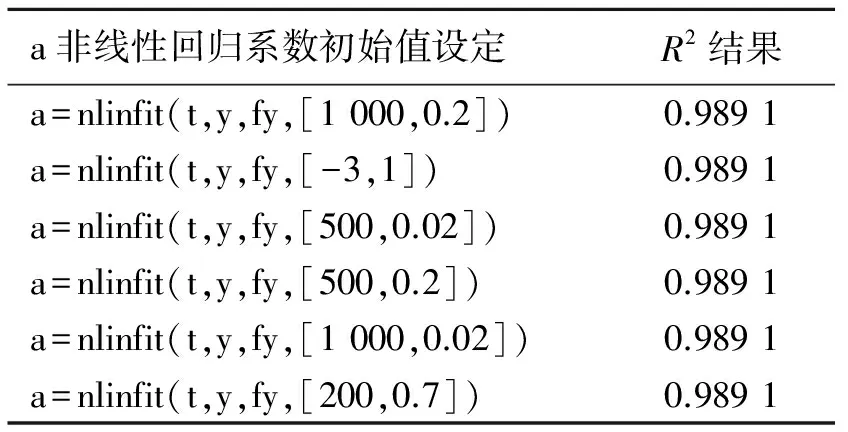
表2 不同初始值拟合结果Tab.2 Effect of different initial values

2)lsqcurvefit最小二乘拟合实现

主要程序如下：

x0=[500,0.02];

[x,norm,res]=lsqcurvefit(@mylogistic,x0,t,y);

y1=mylogistic(x,t);

R2=0.9666

而且可以验证这种方法对初值选择有比较大的容忍度，且容易实现，拟合系数R2接近于1，具体数据见图2，拟合结果见表3.

3)lsqnonlin求最优解拟合

最小二乘法(least square method)，通过最小误差的平方和寻找数据的最佳函数匹配，可用于曲线拟合.在MATLAB 5.x中，用函数leastsq[8]，在MATLAB 2016a中使用lsqnonlin.

function f=cf1(a)

t=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35];

y=[450.6,458.8,467.6,474.0,480.0,485.3,491.5,500.5,510.7,521.4,557.8,565.1,570.9,581.2,588.6,600.3,607.6,614.8,622.7,631.6,665.9,677.0,687.7,697.7,708.2,716.0,724.3,735.6,743.6,752.1,866.1,885.7,903.1,919.1,937.8,956.9];

f=a(1)/(1+(a(1)/450.6-1))*exp(-1.62*a(2)*t);

end

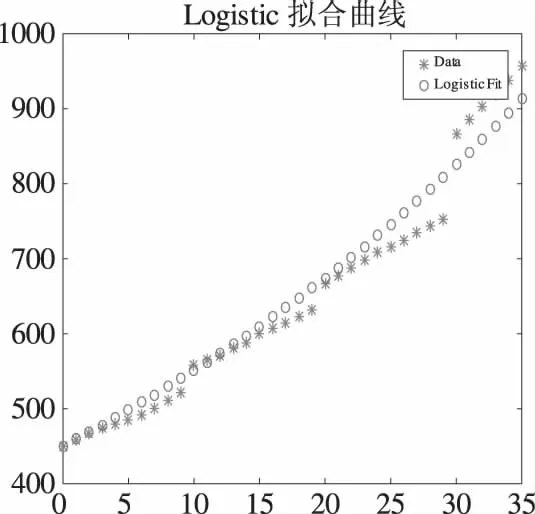
图2 lsqcurvefit最小二乘拟合Fig.2 The performance of lsqcurvefit nonlinear fitting

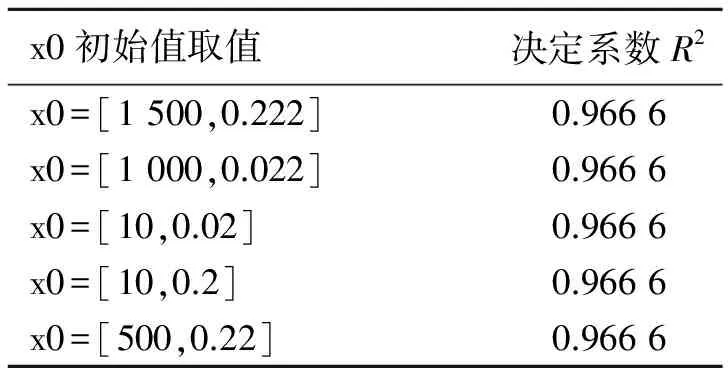
表3 不同初始值拟合结果Tab.3 Effect of different initial values

以文件名cf1.m存盘(文件名与函数名应一致)，然后在MATLAB的工作窗口输入语句： a0=[1,1];a=lsqnonlin (@cf1,a0);成功取得最优解为：a=[331.030 9,5.265 7]，R2= -3.055 1，拟合结果较差.进行其他多次尝试,都没有好的拟合结果(表4).这种方法最优解的收敛与初值选择很有关系，初值选择不好，拟合出的参数结果较差，试解很多次，仍然找不出适合的参数值.此命令在进行二孩人口建模时不适用.

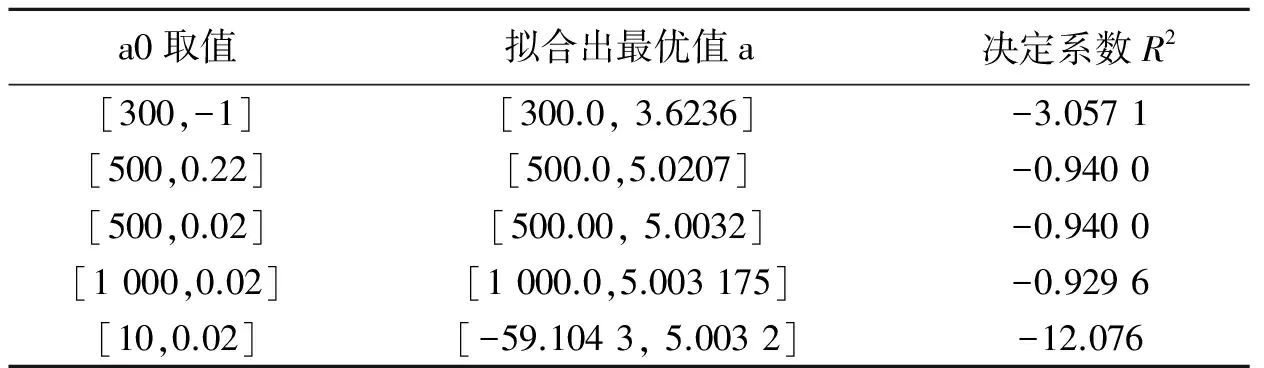
表4 不同初始值拟合结果

2.2 非线性曲线线性化拟合

1)求导后用polyfit进行多项式线性拟合

主要程序如下：

>> x0=450.6;

>>y=diff([x0 x])./(1*x);%一阶求导

>> A=polyfit(x,y,1);%多项式线性曲线拟合

>> polyval(A,t)%多项式在x处的拟合值y

>> r=A(:,2)；s=-A(:,1)；xm=r/s;

此时，xm = 95.646 8，r =-0.003 5，此时R2 =0.911 8.人口模型参数为

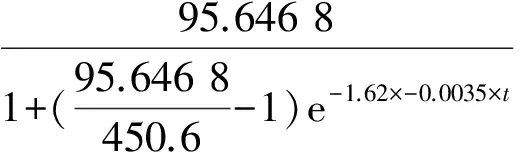
(4)

拟合图与原始图对比曲线见图3.

2)线性化后regress回归

将dx/dt=rx(1-x/xm)改为：(dx/dt)/x=r-sx,其中s=r/xm这样对r,s的估计是线性的，左边可用数值微分计算.主要程序如下：

>> dx=diff(x);dxx=dx./x(1:35); dxx=dxx′; tt=x(1:35); z=[ones(35,1) tt′];

>> b=regress(dxx,z);z(1)=-b(1)/b(2);z(2)=b(1);

>> y1=mylogistic(z,t);

由图4可知，拟合结果较差，不宜采用此方法.

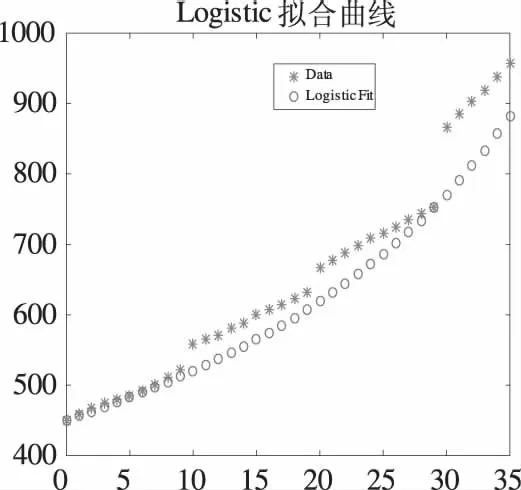
图3 求导后多项式polyfit拟合Fig.3 The performance of polyfit linear fitting after derivation

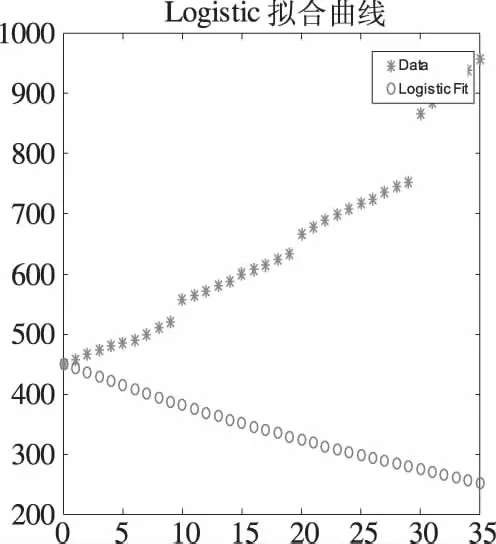
图4 线性化后regress回归Fig.4 The performance of regress after linearization

3 结论

在用MATLAB做非线性回归时，实现的方法有很多种，而且不同的初始值和不同的实现方法会影响到拟合函数是否可有效利用，需要进行不断地尝试.可得出以下结论：

1) 曲线非线性化直接拟合结果优于曲线线性化拟合结果.

2) 用nlinfit函数进行非线性Logsitic改进模型拟合时，在确定系数时，对初值的容忍度较大，拟合系数R2=0.989 1，拟合性能优于lsqcurvefit最小二乘拟合，是实现方法中性能最好的.

3) lsqcurvefit最小二乘拟合进行Logsitic改进模型拟合时，对初值设置的宽容度较大，比较容易实现，拟合系数R2=0.966 6，虽然拟合系数稍劣于nlinfit拟合，但是R2接近于1，由此方法确定的函数模型可以接受.

4) lsqnonlin函数在其他函数建模中表现出较好的性能，但是在二孩人口建模时找的最优解拟合性能很差，无法采用.

[1] 郑州市统计局.历年人口数[EB/OL]. 2017-01-01[2017-02-09].http://tjj.zhengzhou.gov.cn/ndsj/216707.jhtml.

[2] 杨益民,付必谦.关于Logistic 增长模型参数估计方法的再探讨[J].统计与决策,2015(13):28-29.

[3] 马莉.MATLAB数学实验与建模[M].北京：清华大学出版社，2010:148-149.

[4] 何正风.MATLAB在数学方面的应用[M]. 北京：清华大学出版社，2012:225-226.

[5] 胡亮. 非线性拟合的初值问题[J]. 吉首大学学报 (自然科学版), 2003, 24(1): 37-39.

[6] 殷祚云. Logistic 曲线拟合方法研究[J]. 数理统计与管理, 2002, 21(1): 41-46.

[7] 谢兰,高东红. 非线性回归方法的应用与比较[J]. 数学的实践与认识, 2009, 39(10): 117-121.

[8] 袁新生, 龙门. 非线性曲线拟合的三种软件解法之比较[J]. 徐州工程学院学报, 2005, 20(3): 74-76.

ResearchedonModelofPopulationGrowthUnderTwo-childPolicyBasedonMATLAB：ACaseStudyofZhengzhouCity

TIAN Haili
(CollegeofMechanicalandTelecommunicationsEngineering,ZhengzhouTechnologyandBusinessUniversity，Zhengzhou451400,China)

Taking factors on bearing second-child into account, based on data of Zhengzhou City in recent years, an population growth model, namely, an improved logistic population model, under two-child policy was presented. Then the parameters were estimated and functions were modeled based on MATLAB 2016a. It focused on two chief factors affecting the performance of curve fitting method with MATLAB: setting of initial parameter value and curve fitting methods. After repeated attempts in variety of implementations with MATLAB，the better method of curve fitting was founded, and the population growth model of Zhengzhou under two-child policy was established finally. Moreover, tested the different nonlinear fitting methods’ tolerance of initial value, and found the best two methods, namely, the nlinfit nonlinear fitting method and the lsqcurvefit least square fitting method.

the population growth model under the two-child policy; MATLAB; logistic regress model; setting of initial parameter value; curve fitting method

2017-04-13

河南省社科联、河南省经团联调研课题“基于二胎政策下人口增长模型对郑州市中小学教育发展的影响”(SKL-2016-697)；2015年河南省教育技术装备和实践教育研究项目“高职移动通信技术专业公共实践教学平台建设研究”(GZS222)

田海丽(1978—)，女，河南开封人，郑州工商学院机械与电信工程学院讲师.

10.3969/j.issn.1007-0834.2017.02.008

TP391

：A

：1007-0834(2017)02-0030-06