基于第一原理计算拟合Ag、Si和C原子间作用势的研究

王永伟,郭永亮,,张伟,柯学志

(1.华东师范大学物理与材料科学学院,上海200241; 2.中国科学院上海应用物理研究所,上海201800)

基于第一原理计算拟合Ag、Si和C原子间作用势的研究

王永伟1,郭永亮1,2,张伟2,柯学志1

(1.华东师范大学物理与材料科学学院,上海200241; 2.中国科学院上海应用物理研究所,上海201800)

为了实现Ag在SiC晶体中扩散的分子动力学模拟,根据第一性原理计算结果,采用“力匹配”方法对Ag、Si和C原子间相互作用势进行拟合,并用晶格常数、内聚能、体弹性模量、弹性常数和缺陷形成能等进行了势函数的验证.结果表明,拟合所得的势对Si、C和SiC晶体的内聚能、晶格常数和体弹性模量的计算非常准确,最大误差不超过0.6%;并且,该势对Si和C晶体中空位与间隙形成能及SiC晶体中Si与C空位形成能的计算值比采用J.Tersoff给出的势的计算值更精确;此外,该势对16种AgSiC三原子体系缺陷形成能的计算也比较精确.

Tersoff势;力匹配;SiC;第一性原理计算

0 引言

弥散在石墨集体中的TRISO(Tristructural-Isotropic)包覆颗粒燃料是高温气冷反应堆的基本元件,从内到外它的基本组成单元依次是:燃料内核(通常是UO2)、多孔石墨缓冲层、内致密热解炭层、SiC层、外热解炭层,如图1所示.在TRISO颗粒中SiC层为其提供了结构支持并且起到阻碍主要核裂变产物扩散的作用[1].虽然SiC层能够有效抑制大部分金属裂变产物的扩散,但是也有实验发现,在高温条件下仍然有Ag等裂变产物透过SiC层扩散到反应堆冷却剂中[1-2].这会导致Ag在反应堆中的积淀,这给核电系统的维护工作造成了很大的困难,同时还存在一定的安全隐患,因为放射性产物110Ag的半衰期比较长,为253 d.

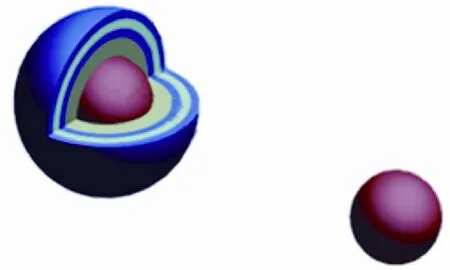
图1 TRISO包覆颗粒燃料结构示意图Fig.1 The structure of Tristructural-Isotropic-coated fuel particle

为了控制裂变产物Ag在SiC层中的扩散,明确其扩散机制是至关重要的.针对Ag在SiC层中的扩散现象,很多扩散机制被提出,其中包括SiC的降解[3-4]、通过裂缝和纳米孔的扩散[5-7]、沿着晶粒边界和错位层的扩散[8-9]等.但是时至今日,究竟是哪一种扩散机制起作用仍然是不明确的,有待于实验和理论工作的进一步验证.

关于Ag在SiC中的扩散,在实验[10-14]和基于密度泛函理论(Density Functional Theory, DFT)的第一性原理[15-16]方面都有相应的研究,其中对Ag扩散系数的计算都是根据计算出来的主要几种点缺陷的形成能和迁移势垒按照公式D=D0exp(−Q/kbT)估算获得;然而没有分子动力学模拟方面的研究,这是因为缺乏相应的原子间相互作用势.众所周知,由于计算条件的限制,第一性原理方法只能在小尺度范围内进行计算研究;而分子动力学方法可以在大尺度下进行长时间的动态模拟,并且可以通过分子动力学模拟对扩散机制的微观过程进行直接观察.分子动力学方法可以用均方位移法或速度关联函数法直接计算扩散系数.对于缺陷迁移这类微观上低概率事件,可以借助于加速分子动力学方法[17]来进行模拟.

进行分子动力学模拟研究需要相应的势函数作为支持,在AgSiC三原子体系中存在Si-Si、C-C、Si-C、Ag-Ag、Ag-Si和Ag-C等6种相互作用关系.但是,现有的势中没有Ag-Si和Ag-C势.况且,已有的Si-Si势、C-C势、Si-C势[18-22]和Ag-Ag势[23]并不是针对我们研究的体系拟合的,需用进一步修正甚至重新拟合.因此,需要建立一个AgSiC三原子体系的相互作用势,为分子动力学方法研究Ag在SiC中扩散提供支持.

1 理论方法

1.1 计算原理及公式

本文中势函数的验证过程中所涉及的体系内聚能、缺陷形成能和体弹性模量等的计算分别采用如下公式.

内聚能的计算公式[24]为

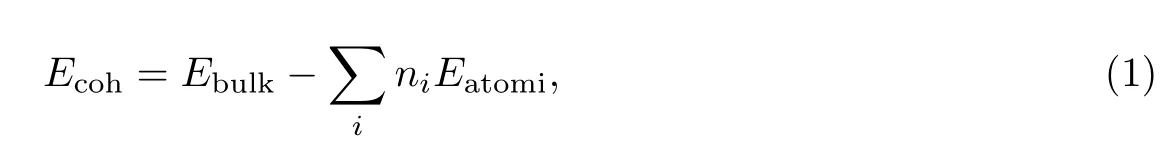
其中,Ebulk和Eatomi分别表示单个化学势晶体能量和单个原子能量(其中包括自旋能和零点振动能两部分).

缺陷形成能的计算公式[15,17]为

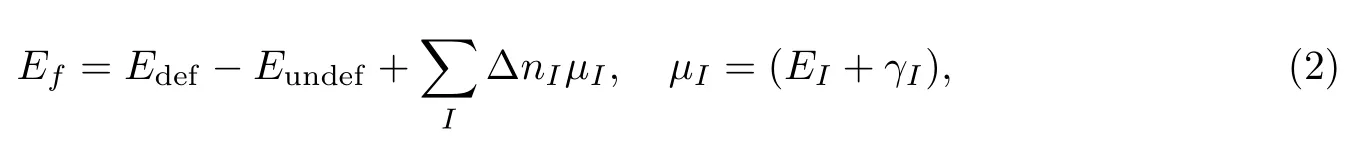
其中,Edef表示包含缺陷的晶胞能量,Eundef表示完整晶胞能量,I表示元素种类,∆nI表示完整晶胞中I类原子数减去缺陷晶胞中I类原子数,µI表示对应化合物构型(SiC晶体)下I类原子的化学势,EI是相应单质构型(在这里就是Ag、Si和C晶体的)下单个I原子的能量,γI表示元素I在相应单质构型下的化学势,可根据文献[25]确定它的取值范围,即, 0≤γI≤ESiC−ESi−EC.这里分3种情况分别取[15]:γSi=γC=(ESiC−ESi−EC)/2; γSi=ESiC−ESi−EC,γC=0;γSi=0,γC=ESiC−ESi−EC.本文计算SiC晶体缺陷形成能时只考虑γC=(ESiC−ESi−EC[15])/2的情况.

晶格常数a、内聚能E、体弹性模量B0等值是通过Murnaghan方程[26]对体积–能量关系的拟合结果获得,Murnaghan方程的一般表达式为

本文采用Tersoff势[21]来描述原子间相互作用,其一般形式为

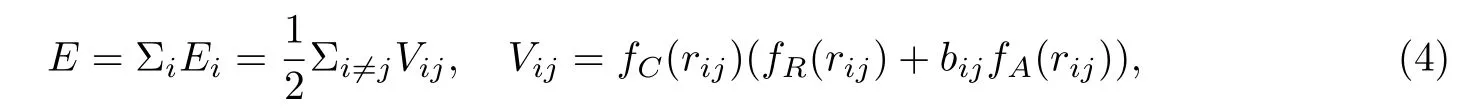
其中,排斥(Repulsive)势fR和吸引(Attractive)势fA如式(5)所示,截断(Cutoff)函数如式(6)所示,即

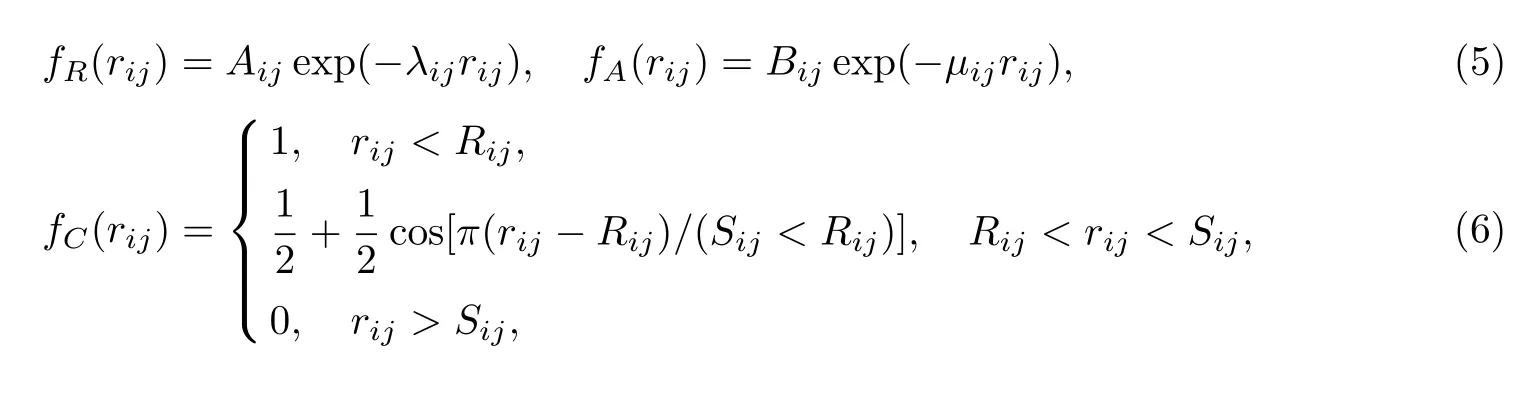
以及表示原子周围环境的三体作用项

式(4)至式(7)中i,j,k表示原子序号,rik表示原子i和k之间的距离,θijk表示ij和ik原子间化学键之间的角度.为了简单起见,令χ=1,则以上各式共有11个待定参数.其中A,B,λ和µ这4个参数为两体相互作用部分,β,n,c,d和h为三体相互作用部分,R,S的取值跟截断半径有关.

在拟合过程中POTFIT采用最小二乘法、共轭梯度法、模拟退火法等,来优化参考构型的力和能量等物理量的第一性原理计算值和势函数计算值之间的差值函数,使之取最小值,从而获得势函数各参量的值.差值函数的一般形式为

其中,

分别代表来自内聚能、力和压强的贡献.在以上各式中Wi表示权重,NC表示所有构型的数目,NA表示所有原子的数目,Fi,xj表示i原子在xj方向受到的力,σi,j表示i原子应力张量的第j个数值.本文拟合时只考虑了式(8)中的能量和力两项对差值函数的影响.

1.2 计算参数设置

本文采用Tersoff势作为Ag、Si和C原子间作用的力场函数,其合理性已经在参考文献[18-22,27]中得到了很好验证.拟合势函数所需的第一性分子动力学、静态优化和电子步优化等计算及验证势函数所需的弹性常数、缺陷形成能、晶格常数和内聚能等第一性原理的计算采用基于密度泛函理论(DFT)的VASP[28]软件包.势函数的拟合采用基于“力匹配”方法的POTFIT[29]软件包.势函数验证过程中用拟合的势计算弹性常数、晶格常数、内聚能、体弹性模量和SiC晶体缺陷形成能等值时采用基于“牛顿力学”的Lammps软件包.

本文用VASP软件包的投影缀加波方法进行密度泛函计算,采用PBE[30]形式的GGA[31]交换关联泛函求解Kohn-Sham方程.平面波截断能取570 eV.Monkhorst-Pack K-point[32]网格:8原子体系取13×13×13;大于60原子体系取7×7×7.在SiC和AgSiC缺陷的第一性分子动力学计算中,步长取1.55 fs,温度参考文献[10-14]中的实验温度取1 073～1 773 K.

Lammps计算过程中涉及的静态优化过程都采用最陡下降算法,步长取1.55 fs.POTFIT优化过程中,体系能量权重取100,退火温度取1 500 K.

2 结果与讨论

2.1 构型选取

在势函数的拟合过程中要选取包含所研究的物理过程或物理条件的晶体结构作为第一性原理计算的构型.为了描述Ag在SiC晶体中的扩散,AgSiC三原子缺陷体系构型的选取David Shrader在文献[15]中提到的16种缺陷作为基本构型,它们分别是AgC、Ag TC、AgCVC、AgCVSi、AgC2VSi、AgCVSiVC、AgCVSiSiC、AgCVSiCSi、AgSi、Ag TSi、AgSiVSi、AgSiVC、AgSi2VC、AgSiVCVSi、AgSiVCSiC和AgSiVCCSi.在这里AgC和AgSi分别表示Ag原子替换了C和Si原子,VSi和VC分别表示在Ag原子最近的Si空位和C空位,它们前面的数字表示空位的数目;SiC和CSi则分别表示1个Si原子替换了离Ag原子最近的C原子和C原子替换了离Ag原子最近的Si原子, Ag TC和Ag TSi则分别表示Ag填隙在4个C的中心和4个Si的中心.为了便于理解,我们画出了其中5种缺陷构型,如图2所示,其中,图2(a)AgSiVC表示Ag原子取代了Si原子的位置,并且在Ag原子的4个最近邻位置之一出现了1个C空位;图2(b)AgSiVCVSi则表示取代Si的Ag原子的四个最近邻位置上出现1个C空位,同时在Ag次近邻位置上出现了一个Si空位;图2(c)AgSi2VC表示取代Si的Ag原子的4个最近邻位置上出现2个C空位;图2(d)AgSiVCCSi表示取代Si的Ag最近邻位置上出现1个C空位,同时次近邻位置的Si被C取代;图2(e)AgSiVCSiC则表示取代Si的Ag最近邻位置上出现1个C空位,同时最近邻位置的另一个C被Si原子取代.其他11种构型表示方法以此类推.

图2 5种AgSiC三原子体系缺陷示意图Fig.2 Five kinds of AgSiC three-atom system defects

本文研究的AgSiC三原子体系的主体是SiC材料,所以在势的拟合过程中要兼顾SiC晶体的一些性质.因此我们首先对Si-Si,C-C和Si-C原子间作用势进行了拟合.在本文中Si-Si、C-C和Si-C原子间Tersoff势的截断半径[21]分别取3.0˚A,2.1˚A和2.5˚A;而在完全优化后的SiC晶格中Si-Si,C-C和Si-C原子间距分别约为3.1˚A、3.1˚A和1.9˚A.Si-Si和C-C间距都为3.1˚A大于对应的势函数截断半径3.0˚A和2.1˚A,因此在计算完美SiC晶体性质时, Si-Si和C-C势对其结果几乎没有影响;而Si-C间距1.9˚A在Si-C势的截断半径2.5˚A之内,因此Si-C作用在SiC晶体性质计算时有很大影响.我们用文献[21]中给出的Tersoff势进行了验证,结果表明,只有在SiC晶体中存在间隙等缺陷时,Si-Si和C-C作用势才会对SiC晶体性质的计算结果产生影响,否则没有影响.这是因为间隙的存在使得Si-Si和C-C原子间距分别在3.0˚A和2.1˚A以下产生了分布.因此,我们认为Si-Si和C-C作用势对SiC晶体性质直接产生的影响很小,可以最先单独进行拟合,这样使得拟合过程快速和简单,并且得到的SiC体系的势还可以兼顾C和Si晶体各自的性质.

基于以上分析,具体拟合过程分3步进行:首先,分别拟合Si-Si和C-C势;然后,固定Si-Si和C-C势的各参数不变进一步拟合Si-C势;最后,固定前两步中的拟合结果不变,进行Ag-Si和Ag-C作用势的拟合.相应构型的选取也分为如下3类.

1.Si-Si和C-C作用势构型

(1)首先,完全优化64原子Si(C)晶格;固定晶格常数分别对65(间隙)、63(空位)原子的Si(C)构型进行等体积优化,并计算相应构型Si(C)原子间距的分布及所对应权重(这里的权重与相同间距出现的次数成正比).Si和C单质体系的间隙、空位结构如图3所示.

(2)根据(1)中原子间距分布,放大或缩小8原子完全优化的晶格,使其原子间距刚好满足(1)中得到的原子间距分布.一般会产生10至20个构型.

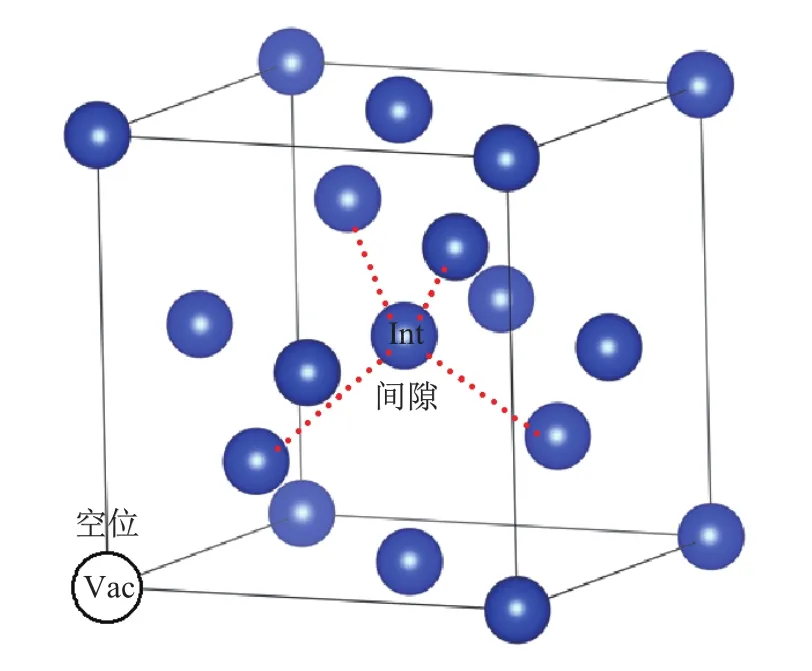
图3 Si(C)晶体中空位和间隙示意图Fig.3 Vacancy and interstitial of Si(C)crystal

2.Si-C作用势构型

(1)状态方程.为了确定SiC晶体的晶格常数、形成能、体弹性模量和弹性常数,我们对SiC完整晶格进行了完全优化(平衡体积为V0),并选取了0.90V0至1.15V0的15个构型.

(2)缺陷.为了初步考虑AgSiC体系中的缺陷,我们对AgC等16种缺陷固定体积进行了优化(采用64原子SiC晶体完全优化的晶格常数),然后去掉缺陷构型中Ag原子并保持原有Si原子、C原子位置不变,进行DFT静态计算(只做电子步计算).缺陷结构参照图2.此外,我们还考虑了SiC中的本征空位VC和VSi两种构型,其结构如图4所示.

图4 SiC晶体中Si和C空位示意图Fig.4 Si and C vacancy of SiC crystal

(3)分子动力学过程.为了获得SiC晶体在相应温度下可能出现的构型及其力和能量等信息,我们取64原子的SiC超胞,采用NVT系综在1 073～1 773 K下进行第一性原理分子动力学计算,每个分子动力学过程进行500步,步长1.55 fs,从轨迹中选取20个不同温度下的构型.

3.Si-Ag和C-Ag作用势构型

(1)缺陷静态优化.对AgC等16种缺陷进行固定体积优化,其晶格常数及体积取完全优化的SiC晶体的值.

(2)缺陷分子动力学过程.为了获得各缺陷体系在相应温度下可能出现的构型及其力和能量等信息,我们用第一性原理分子动力学方法对AgC等16种缺陷在NVT系综下运行500步,步长1.55 fs,温度1 073∼1 773 K.每种缺陷在不同温度下选取10个构型.

2.2 拟合过程

拟合过程中,首先,根据第2.1节中所述的3类构型选取构型,并用第一性原理计算各构型的力和能量等信息.然后,用POTFIT最优化Tersoff势函数中的11个待定参数,调整各参数的变化范围直到结果收敛.最后,用所得的Tersoff势计算各体系晶格常数a、内聚能E、弹性常数Cij、体弹性模量B0、缺陷形成能和16种缺陷的内聚能,并跟第一性原理计算结果进行对比,根据对比结果调整各个构型的权重,反复拟合,直到对比结果相吻合.

在Si-Si和C-C势的拟合过程中,我们只对B、λ和µ这3个参数进行了改动,其他参数借鉴文献[21]中的数值保持不变.之所以这么做是由于本文拟合基于第一性原理计算,而文献中[21]中的拟合基于实验数据,两者能量不匹配,而A、B、λ和µ等参数主要确定体系能量的高低,这里B、λ和µ参数足以达到能量匹配的效果;R和S参数确定相互作用势的截断范围,β、n、c、d和h跟原子周围环境因素有关,都可以不用改变.

在拟合Si-C势的拟合过程中,除了表示截断的R和S这2个参数与文献[21]保持一致外,其他参数都进行了改变.这是由于除了能量不匹配外,本文考虑的缺陷与文献[21]中考虑的缺陷不完全同,从而部分原子的周围环境因素不完全相同,跟周围环境因素有关的参数需用重新拟合.

在Ag-Si和Ag-C作用势的拟合过程中,β和n参数的选取参考了文献[33]中的结果直接取1,R和S的取值结合SiC晶体中原子最近邻和次近邻间距进行调整.

2.3势的验证及结果

由第一性原理计算的Si、C和SiC晶体的晶格常数、内聚能、体弹性模量、弹性常数、缺陷形成能等物理量见表1 DFT所示.这些数据作为势函数验证的主要依据,其准确性决定验证环节的可靠程度.因此我们拿这些数据跟其他第一性原理计算结果(表1 Refa和Refb)进行了对比,由表1 DFT、Refa和Refb的数据可以看出,本文的第一性原理计算值跟其他第一性理论计算值非常接近,其误差跟计算条件及精度有关,可以接受.

图5中(a)、(b)和(c)分别给出了Si、C和SiC晶体的内聚能-体积关系及用Murnaghan方程拟合的结果.图中,纵坐标为平均每个原子的内聚能,横坐标为平均每个原子的体积,黑色“△”、蓝色“□”和红色“○”分别表示文献[21]中所给出的势(Tersoff)、第一性原理(DFT)和本文拟合的势(This work)的计算值,相应的同种颜色曲线代表Murnaghan方程拟合结果.由图5可以看出,由第一性原理数据的Murnaghan曲线(蓝色)和本文给出的势的数据的Murnaghan曲线(黑色)基本重合,两者符合得很好.由Murnaghan方程拟合得到的晶格常数、内聚能和体弹性模量的值见表1所示.

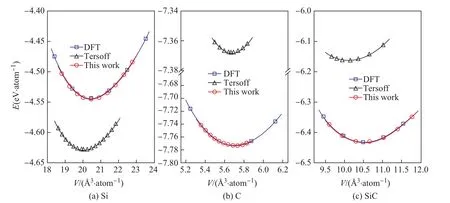
图5 Si、C和SiC晶体在不同体积下内聚能的计算值及用Murnaghan方程拟合的结果Fig.5 The calculated values of cohesive energies at different volumes in Si,C and SiC crystals and the Murnaghan equation fitting results of these values

表1给出了用本文拟合得到的势计算获得的Si、C和SiC晶体中晶格常数a、内聚能E、体弹性模量B0、弹性常数Cij、空位形成能Vac、间隙形成能Int、Si空位形成能VSi和C空位形成能VC等物理量数值,并跟第一性原理计算值、实验值及别人第一性原理计算值等对比.其中,exp、Tersoff和Ref分别表示实验值、文献[21]中势函数的计算值和参考文献的第一性原理计算值,相应的数据来源已在表格中标出;This work和DFT分别表示本文拟合所得势的计算值和第一性原理计算值;空位Vac、间隙Int、Si空位VSi和C空位VC的结构如图3和图4所示.由表1(a)和表1(b)可以看出,本文拟合的势对Si和C晶体的晶格常数、内聚能、弹性常数和体弹性模量的计算值跟第一性原理计算值非常吻合;而对Si和C晶体中空位和间隙形成能的计算值跟文献[21]给出势的计算值比较接近,但与其相比更接近第一性原理计算值,其结果有所改善;这是由于我们在Si-Si和C-C势的拟合过程中只拟合了B、λ和µ这3个参数,同时在构型选取时考虑了缺陷体系的原子间距分布的缘故.由表1(c)SiC可以看出,本文拟合的势对其他物理量的计算值跟第一性原理计算值吻合得很好.

表1 Si、C和SiC晶体中各物理量的计算值Tab.1 The calculated values of various physical quantities in Si,C and SiC crystals

表2给出了计算AgSiC缺陷形成能所需的化学势的值,并与文献[15]中的数据进行了对比,其计算方法及物理意义已在第1.1节中介绍.由第1.1节中的介绍可知,本文和文献[15]中给出的各化学势的差异归根结底是ESi、EC和ESiC值的不同.文献[15]中取块体能量–5.44 eV、–9.20 eV和–15.08 eV作为它们的值,本文取内聚能–4.545 eV、–7.773 eV和–12.862 eV作为它们的值.考虑Si和C的原子能–0.880 eV和–1.316 eV后,根据式(1)可由内聚能计算块体能,其值分别为–5.425 eV、–9.089 eV和–15.059 eV.这跟文献[15]中给出的值仍然有微小差别,这是由于计算精度及方法不同所致.

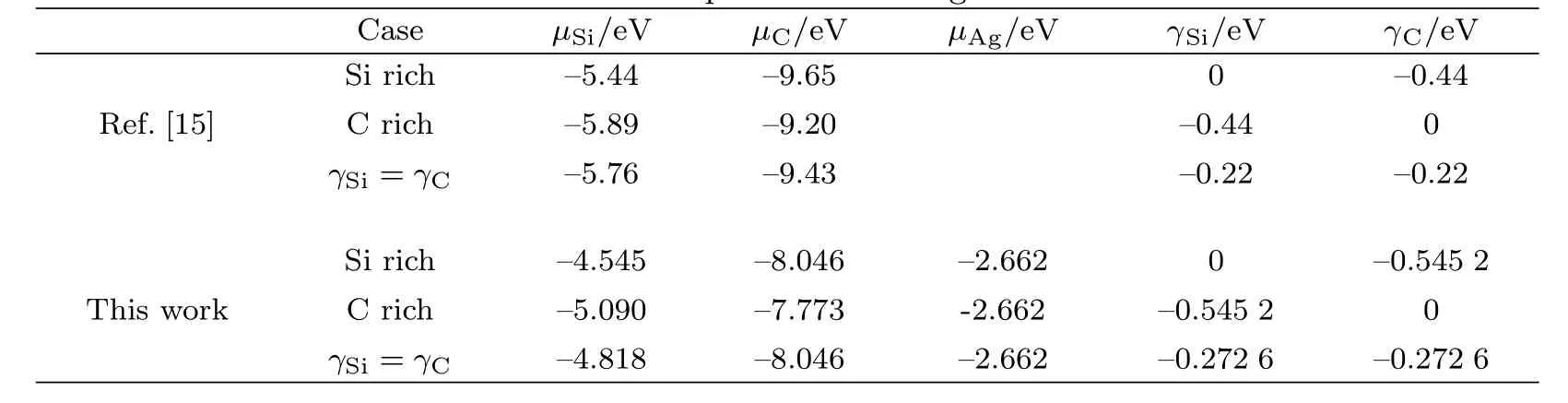
表2 Ag、Si和C的化学势Tab.2 Chemical potentials for Ag、Si and C

表3给出了本文拟合的势对16种AgSiC三原子体系缺陷形成能的计算值跟第一性原理计算值及文献[15]中给出的值的对比结果及相对误差.可以看出,本文拟合的势计算16种AgSiC体系缺陷形成能的值与第一性原理计算的值符合得很好.除了AgCVSiVC、AgCVSiSiC、AgCVC和AgSiVCSiC4这种缺陷形成能误差分别为2.12 eV、2.31 eV、4.83 eV和2.31 eV外,其他缺陷形成能的误差都不超过0.84 eV.由于我们考虑的缺陷种类较多,缺陷结构差异较大,拟合得到的势很难顾及到每一个缺陷的性质,这是经验势本身的局限性所致.个别构型的缺陷形成能显得大,但这也是可以接受的.如参考文献[20-21]中的势对int(S)和VSi+VC缺陷形成的计算值跟第一性原理计算值的最大误差分别为6.7 eV和5.3 eV,相对误差分别为40%和42%.

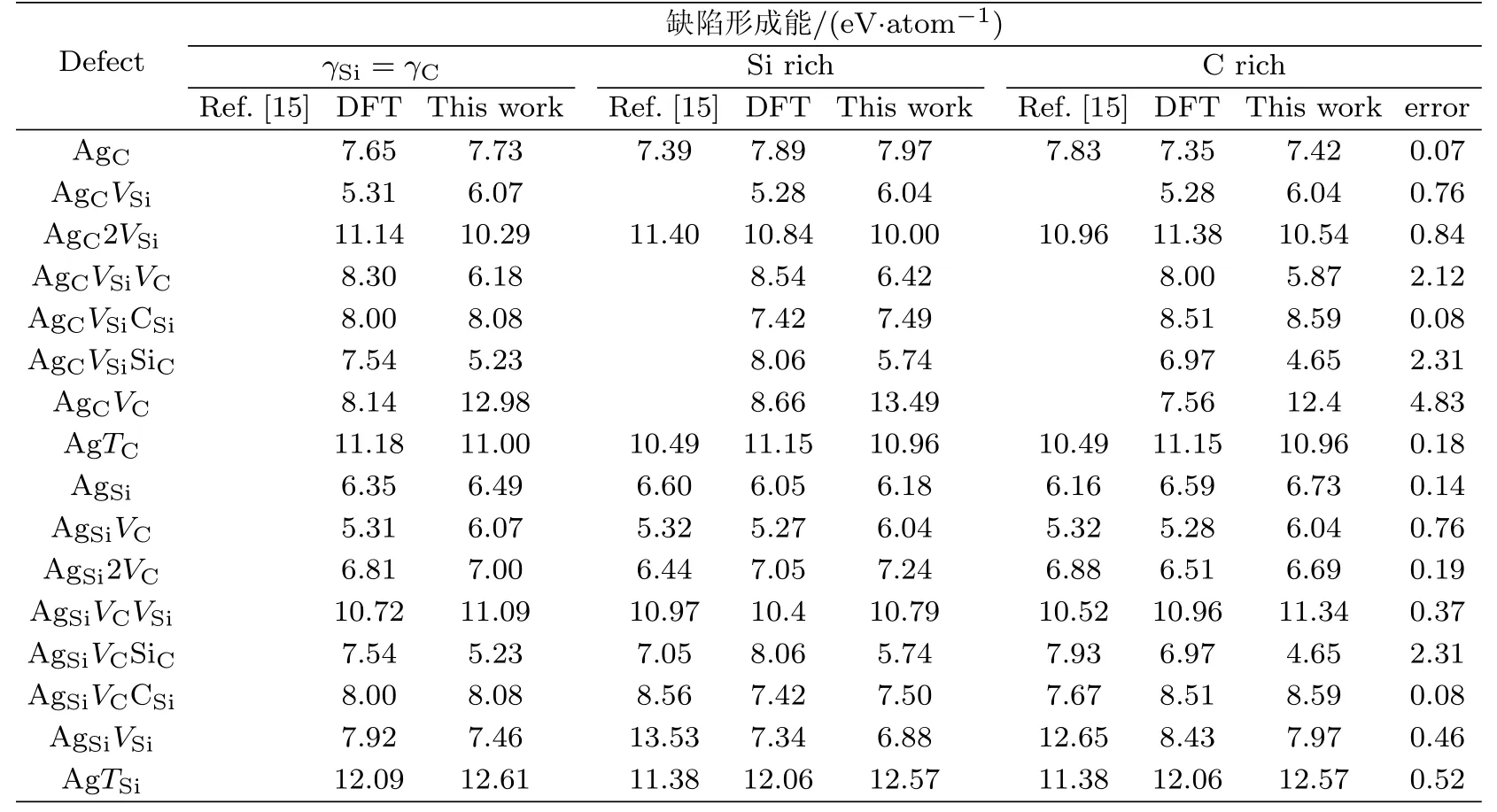
表3 16种缺陷体系缺陷形成能的计算值Tab.3 The calculated formation energies of 16 kinds of defect systems

最终得到的Si、C和Ag原子间相互作用势参数如表4所示,本文所研究的缺陷体系中只有一个Ag原子,故暂不考虑Ag原子间相互作用,Ag-Ag势参数手动设置使之为零.我们用表4中的势分别计算了Si、C和SiC的多个物理量并跟实验值(exp)进行了对比,如表1所示,两者有一定的差别,这是由于我们的拟合是基于第一性原理计算进行的.这个误差的根源是第一性原理计算结果和实验结果之间的差别.总体上来说我们的拟合是成功的.

表4 Si、C和Ag原子间相互作用势参数表Tab.4 Interatomic potential parameters of Si,C and Ag

3 结论

本文采用“力匹配”方法,基于第一性原理计算拟合了存在辐照缺陷的SiC晶体结构中Ag、Si和C原子间相互作用势.这种方法避免了传统的基于实验数据拟合势的方法中数据源不足的问题,为复杂体系材料原子间作用势的拟合提供了可能.拟合结果表明,通过该方法获得的原子间相互作用势能够很好地描述Si、C和SiC晶体材料的晶格常数、内聚能、弹性模量和缺陷形成能等.采用Tersoff形式的势来描述Ag掺杂的SiC晶体结构中Ag、Si和C原子间相互作用行之有效,不但可以兼顾Si、C和SiC晶体各自的性质,而且还能准确计算AgSiC体系的缺陷形成能.当然,由于经验势本身的局限性,我们对缺陷形成能的拟合中,个别构型的误差还是较大,这方面还有一定的提升空间.为拟合更为精确的势,需要更加全面地去考虑各个因素的影响,我们的现有结果为进一步的研究奠定了初步基础.

[1]RUBIN S D.TRISO-coated particle fuel phenomenon identifi cation and ranking tables(PIRTs)for fi ssion product transport due to manufacturing,operations and accidents[R].USA:US-NRC,2004.

[2]VERFONDERN K.Fuel performance and fi ssion product behavior in gas-cooled reactors No.TECDOC-978[R]. Vienna:IAEA,1997.

[3]MINATO K,SAWA K,KOYA T,et al.Fission product release behavior of individual coated fuel particles for high-temperature gas-cooled reactors[J].Nucl Technol,2000,131:36-47.

[4]SCHENK W,POTT G,NABIELEK H.Fuel accident performance testing for small HTRs[J].J Nucl Mater, 1990,175:19-30.

[5]MINATO K,OGAWA T,FUKUDA K,et al.Release behavior of metallic fi ssion products from HTGR fuel particles at 1 600 to 1 900°C[J].J Nucl Mater,1993,202:47-53.

[6]FRIEDLAND E,MALHERBE J B,VANDERBERG N G,et al.Study of silver diff usion in silicon carbide[J].J Nucl Mater,2009,389:326-331.

[7]MACLEAN H,BALLINGER R,KOLAYA L,et al.The eff ect of annealing at 1500˚C on migration and release of ion implanted silver in CVD silicon carbide[J].J Nucl Mater,2006,357:31-47.

[8]BULLOCK R E.Fission-product release during postirradiation annealing of several types of coated fuel particles[J].J Nucl Mater,1984,125:304-319.

[9]PETTI D,BUONGIORNO J,MAKI J,et al.Key diff erences in the fabrication,irradiation and high temperature accident testing of US and German TRISO-coated particle fuel,and their implications on fuel performance[J]. Nucl Eng Des,2003,222:281-297.

[10]NABIELEK H,BROWN P E,OFFERMAN P.Silver release from coated particle fuel[J].Nucl Technol,1977, 35:483-493.

[11]VERFONDERN K,MARTIN R C,MOORMANNN R.Methods and data for HTGR fuel performance and radionuclide release modeling during normal operation and accidents for safety analyses No.JUEL-2721[R]. Germany:Forschungszentrum J¨ulich GmbH,1993.

[12]AMIAN W,STOVER D.Diff usion of silver and cesium in silicon-carbide coatings of fuel particles for hightemperature gas-cooled reactors[J].Nucl Technol,1983,61:475-486.

[13]FRIEDLAND E,MALHERBE J B,VANDERBERG N G,et al.Study of silver diff usion in silicon carbide[J]. J Nucl Mater,2009,389:326-331.

[14]MACLEAN H J.Silver transport in CVD silicon carbide[D].Boston:MIT,2004.

[15]SHRADER D,KHALIL S,GERCZAK T,et al.Ag diff usion in cubic silicon carbide[J].J Nucl Mater,2010,408: 257-271.

[16]KHALIL S,SWAMINATHAN N,SHRADER D,et al.Diff usion of Ag alongΣ3 grain boundaries in 3C-SiC[J]. Phys Rev B,2011,84:214104.

[17]VOTER A F.Hyperdynamics:Accelerated molecular dynamics of infrequent events[J].Phys Rev Lett,1997,78: 3908-3911.

[18]TERSOFF J.New empirical approach for the structure and energy of covalent systems[J].Phys Rev B,1988, 37:6991-7000.

[19]TERSOFF J.New empirical model for the structural properties of silicon[J].Phys Rev Lett,1986,56:632-635.

[20]TERSOFF J.Empirical interatomic potential for carbon,with applications to amorphous carbon[J].Phys Rev Lett,1988,61:2879-2882.

[21]TERSOFF J.Modeling solid-state chemistry:Interatomic potentials for multicomponent systems[J].Phys Rev B,1989,39:5566-5568.

[22]TERSOFF J.Empirical interatomic potential for silicon with improved elastic properties[J].Phys Rev B,1988, 38:9902-9905.

[23]FOILES S M,BASKES M I,DAW M S.Embedded-atom-method functions for the fcc metals Cu,Ag,Au,Ni, Pd,Pt,and their alloys[J].Phys Rev B,1986,33:7983-7991.

[24]LI X P,CEPERLEY D M,MARTIN R M.Cohesive energy of silicon by the Green’s-function monte carlo method[J].Phys Rev B,1991,44:10929-10932.

[25]KOHAN A F,CEDER G,MORGAN D,et al.First-principles study of native point defects in ZnO[J].Phys Rev B,2000,61:15019-15027.

[26]MURNAGHAN F D.The compressibility of media under extreme pressures[J].Proceeding of the National Academy of Sciences of the United States of America,1944,30(9):244-247.

[27]BUTLER K T,VULLUM P E,MUGGERUD A M,et al.Structural and electronic properties of silver/silicon interfaces and implications for solar cell performance[J].Phys Rev B,2011,83(23):2155-2161.

[28]KRESSE G,FURTHMULLER J.Effi cient iterative schemes for ab initio total-energy calculations using a planewave basis set[J].Phys Rev B,1996,54(16):11169-11186.

[29]BROMMER P,G¨AHLER F.Potfi t:Eff ective potentials from ab-initio data[J].Simul Mater Sci Eng,2007,15: 295-304.

[30]PERDEW J P,BURKE K,ERNZERHOF M.Generalized gradient approximation made simple[J].Phys Rev Lett,1996,77:3865-3868.

[31]MARTIN R M.Electronic Structure:Basic Theory and Practical Methods[M].Cambridge:Cambridge University Press,2004.

[32]MONKHORST H J,PACK J D.Special points for Brillouin-zone integrations[J].Phys Rev B,1976,13:5188-5200.

[33]ERHART P,ALBE K.Analytical potential for atomistic simulations of silicon,carbon,and silicon carbide[J]. Phys Rev B,2005,71(3):035211.

[34]MOORE C E.Atomic Energy Levels Volumer[M].Washington D C:NBS,1949.

[35]AADERSON O L.The use of ultrasonic measurements under modest pressure to estimate compression at high pressure[J].J Phys Chem Solids,1966,27:547-565.

[36]DONOHUE J.The structures of the elements[J].Diamond and Related Materials,1974,24(4):436.DOI: 10.1016/j.diamond.2011.01.035.

[37]YIN M T,COHEN M L.Microscopic theory of the phase transformation and lattice dynamics of Si[J].Phys Rev Lett,1980,45:1004-1007.

[38]CAR R,KELLY P J,OSHIYAMA A,et al.Microscopic theory of atomic diff usion mechanisms in silicon[J]. Phys Rev Lett,1984,52:1814-1817.

[39]BARAFF G A,SCHLUTER M.Migration of interstitials in silicon[J].Phys Rev B,1984,30:3460-3469.

[40]BREWER L.Lawrence berkeley laboratory report No.LB-3720[R].California:Lawrence Berkeley Laboratory, 1977.

[41]MCSKIMIN H J,ANDREATCH P.The elastic stiff ness moduli of diamond[J].J Appl Phys,1972,43:985-987.

[42]BERNHOLC J,ANTONELLI A,DELSOLE T M,et al.Mechanism of self-diff usion in diamond[J].Phys Rev Lett,1988,61:2689-2692.

[43]LEE D H,JOANNOPOULOS J D.Simple scheme for deriving atomic force constants:Application to SiC[J]. Phys Rev Lett,1982,48:1846-1849.

(责任编辑：李艺)

Interatomic potential fi tting study of Ag,Si and C based on
fi rst-principle calculations

WANG Yong-wei1,GUO Yong-liang1,2,ZHANG Wei2,KE Xue-zhi1
(1.School of Physics and Materials Science,East China Normal University, Shanghai 200241,China; 2.Shanghai Institute of Applied Physics,Chinese Academy of Sciences, Shanghai 201800,China)

In order to perform molecular dynamics simulations of Ag diff usion in SiC crystals,we use”force-matching”method to fi t the interatomic interaction potentials of Ag, Si and C based on fi rst-principle calculations.The eff ectiveness of our obtained potential functions are verifi ed by the calculations of the lattice constants,cohesive energies,bulk modulus,elastic constants and defect formation energies,etc.The results show that the values of cohesive energies,lattice constants and bulk modulus can be calculated precisely by our potentials,and the maximum error does not exceed 0.6%.The values of vacanciesand interstitial formation energies of Si and C crystals and Si and C vacancy formation of SiC crystals calculated by our potentials are more accurate than that calculated by J.Tersoff’s potentials.In addition,the formation energies of the 16 kinds of AgSiC three-atom defect systems can also be calculated accurately by our potentials.

Tersoff potential;force-matching;SiC;first-principle calculations

O411.2;O483;O414.2

A

10.3969/j.issn.1000-5641.2017.04.010

1000-5641(2017)04-0114-12

2016-07-22

王永伟,男,硕士研究生,研究方向为统计和凝聚态理论.E-mail：wangyongwe13@163.com.

柯学志,男,教授,博士生导师,研究方向为统计和凝聚态理论. E-mail：xzke@phy.ecnu.edu.cn.郭永亮,男,博士研究生,研究方向为统计和凝聚态理论.E-mail：ylguo@stu.ecnu.edu.cn.