覆盖空间在多连通积分定理证明中的运用
胡光明,龙见仁
(1.北京航空航天大学数学与系统科学学院,北京100191; 2.贵州师范大学数学科学学院,贵阳550001)
覆盖空间在多连通积分定理证明中的运用
胡光明1,龙见仁2
(1.北京航空航天大学数学与系统科学学院,北京100191; 2.贵州师范大学数学科学学院,贵阳550001)
众所周知,单连通区域上解析函数所确定的变上限积分是一个单值函数,然而对于多连通区域D上解析函数f(z)的变上限积分F(z)=∫zz0f(ζ)dζ,F(z)不仅依赖于z(z0是D内固定的一点),还依赖以下两点:(1)积分的路径;(2)函数f(z)关于洞是否恰当.由此可以知道F(z)可能是一个多值函数.以上结果均可以在一般复变函数教材中找到,这里不再赘述.本文利用黎曼曲面的正则覆盖曲面知识,给出了解析函数f(z)在多连通区域上积分的一种新诠释.
多连通区域;正则覆盖曲面;覆盖变换群;恰当微分;交换群
0 引言
本文考虑了多连通区域D上解析函数f的变上限积分F(z)=f(ζ)dζ,F(z)不仅依赖于z(z0是D内固定的一点),还依赖于积分的路径选取和函数f(z)关于洞是否恰当,因此F(z)可能是一个多值函数.本文从黎曼曲面的正则覆盖曲面的角度给出了定理的一个新诠释.本文主要定理如下.
定理0.1设f是平面区域D上的解析函数,a是D内固定的一点,对于任意p∈D存在一条路径
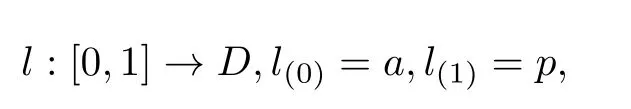
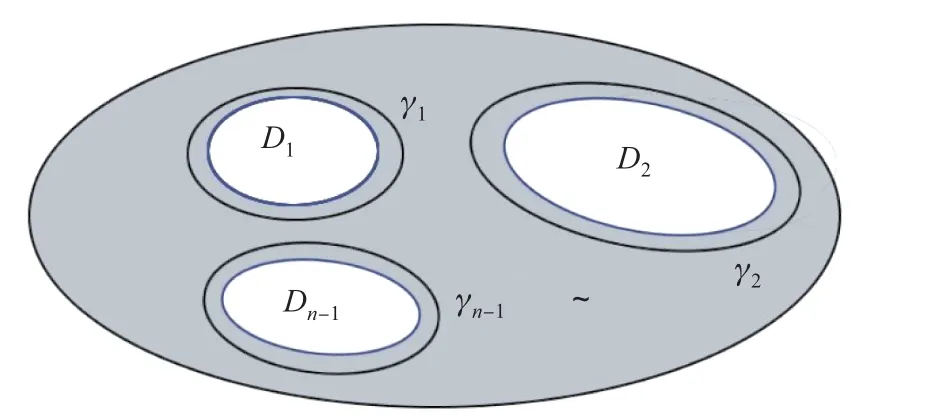
图1 n连通Fig.1 n-connection
定理0.2设D是n连通区域,f(z)在D内解析,这里将n−1个洞编序D1,D2,···, Dn−1,如图1所示.
(1)若f(z)d z是恰当微分,则
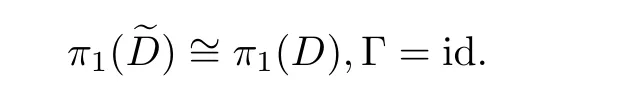
(2)若f(z)d z不是恰当微分,则
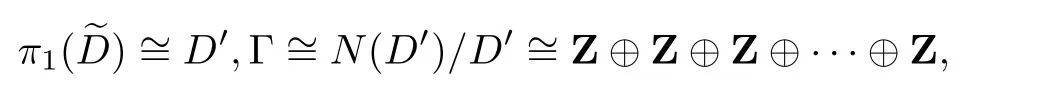
其中Z的个数由f(z)沿洞的简单闭曲线γ1,γ2,···,γn−1积分不为0的个数决定.
推论设D是n连通区域,f(z)在D内解析,这里重新将沿洞的简单闭曲线γ1,γ2,···,γn−1积分不为0的洞编序为对应的简单闭曲线为则F(z)=∫f(ζ)dζ一个单值分支的表达式
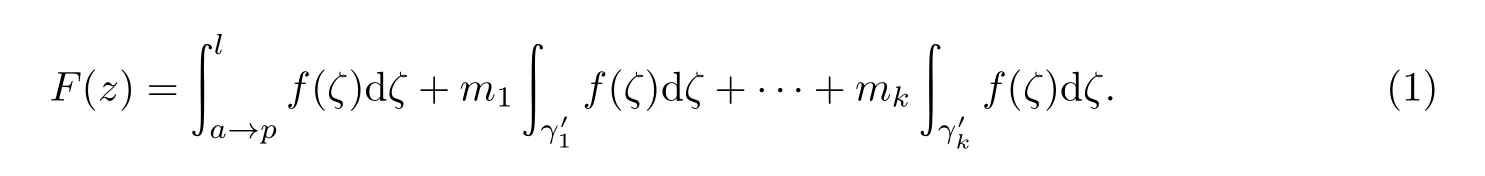
下面给出一个简单的例子.
例子设D∗是单位圆挖去一个原点,f(z)在D内解析,则F(z)=f(ζ)dζ会出现以下两种情况.
1 预备知识
记号说明如下.
(1)记[γ]表示曲线γ的同伦类,π1(D)表示D上的基本群,π1()表示上基本群.
(2)设D是n连通区域,它的有界余集有n−1个,分别为D1,D2,···,Dn−1,令γi表示围绕Di的简单闭曲线,那么我们知道{[γi]|i=1,···,n−1}生成π1(D).
(3)记D′为π1(D)的全体换位子所生成的群,即
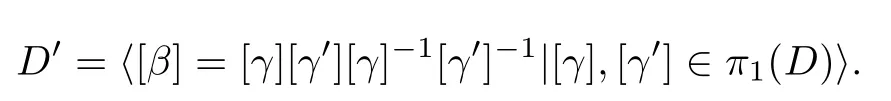
(4)B(p0,r)表示以p0为圆心,半径是r的开圆盘.
(5)对于任意q∈B(p0,r),定义p0与q的一条道路
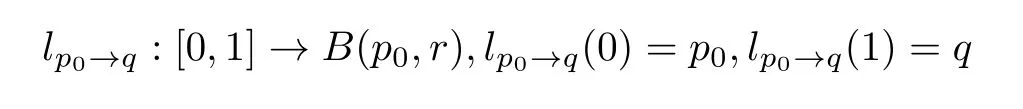
为连续映射.
(6)我们称一个微分为恰当微分,若存在一个低一阶的微分形式,使其外微分恰好等于给定的微分形式.
定理的证明还需要下面的引理.
引理1.1[1]是W的正则覆盖曲面,π1(W)是W的基本群,Γ是(˜W,π)上的覆盖变换群,则对于任意G<π1(D),有
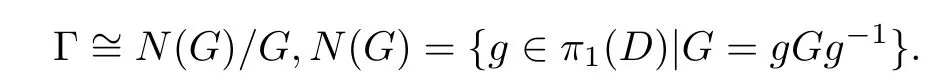
引理1.2[1]设是W的正则覆盖曲面,p是W上的一点,设∈π−1(p),则满足的覆盖变换是唯一的.
引理1.3[2]设G′是G的换位子群,则G/G′是交换群.
2 定理及推论的证明
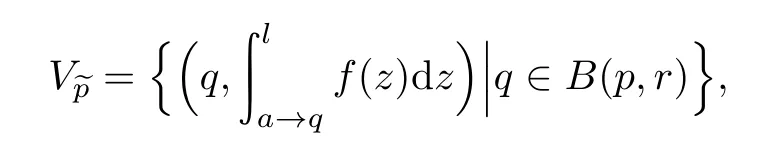
全体邻域基构成的族记为β.
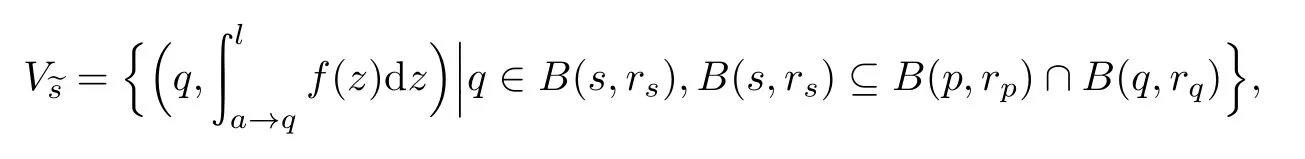
则˜D的子集族
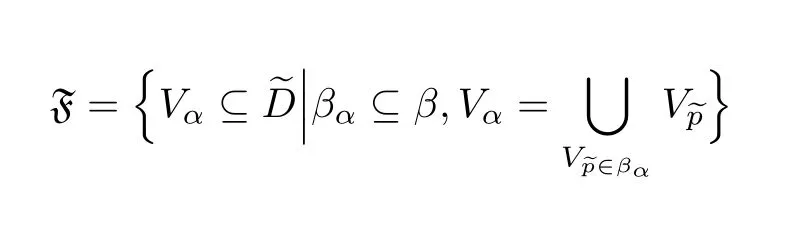
(2)我们将验证F为Hausdorff空间.
分两种情况考虑.
1)p1p2.则存在p1,p2的两个邻域B(p1,r1),B(p2,r2),满足
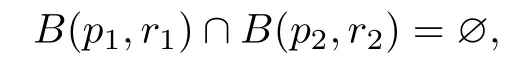
2)p1=p2.此时取两条不同的道路l1,l2,满足
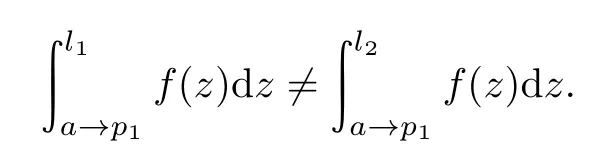
对于任意的p∈B(p1,r),我们取相互同伦两条路径δ1,δ2连接p1,p.由Cauchy定理[4]可知f(z)d z=∫f(z)d z,所以我们得到
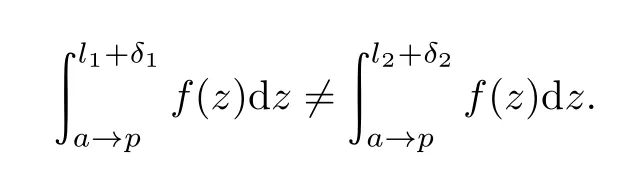
由邻域的定义可知存在V˜p1与V˜p2满足V˜p1∩V˜p2=∅,所以为Hausdorff空间.
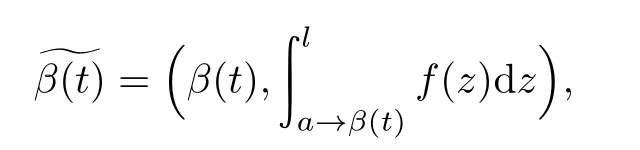
其中道路la→β(t)同伦于道路la→q1•β([0,t]),我们要证明˜β(t)的连续性,对于任意一点t0∈[0,1],
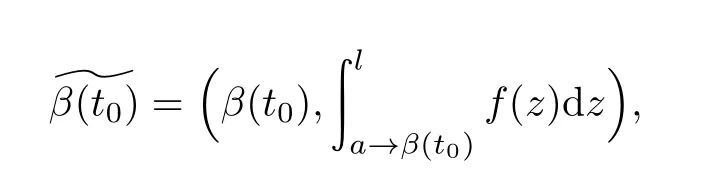
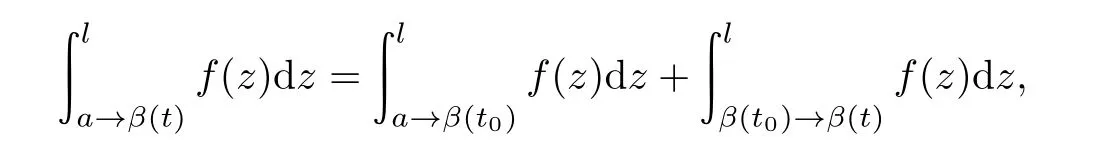
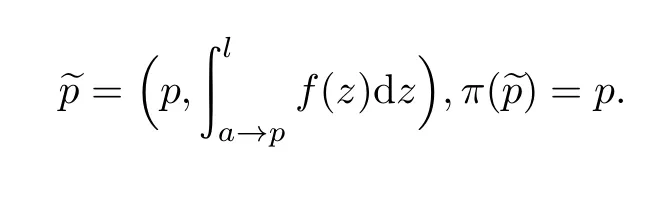
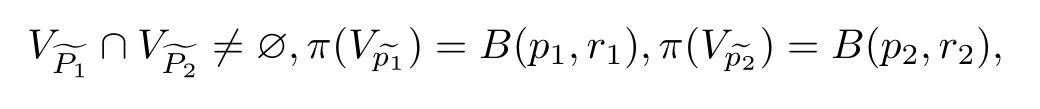
则
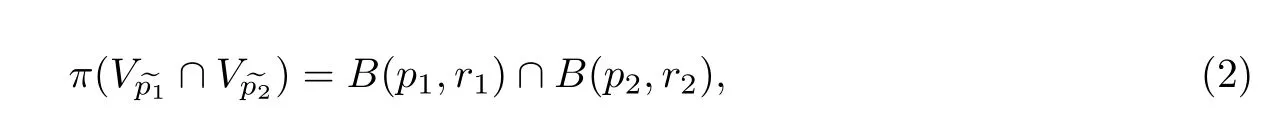
定理0.2的证明(1)设f(z)d z是恰当微分,由于恰当微分在任一闭链上的积分都为0,故对任意
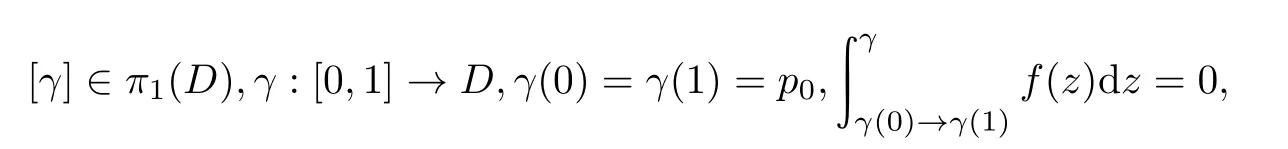
此时p0的所有的上方点都为(p0,0),记为那么γ的提升总是闭曲线,所以∼= π1(D).由引理1.2知,覆盖变换就是由同一点的所有上方点间的变换组成的,f(z)d z是恰当微分时,任意p0的所有上方点都是一样的,故此时的所有覆盖变换都是恒等变换,因而˜D的覆盖变换群Γ={id}.
(2)设f(z)d z不是恰当微分,则f(z)d z在任意闭链上的积分可能为0,可能不为0,但是对于任意两条闭曲线α和β,令
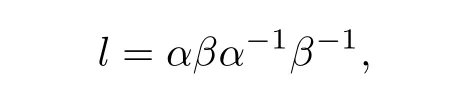
则
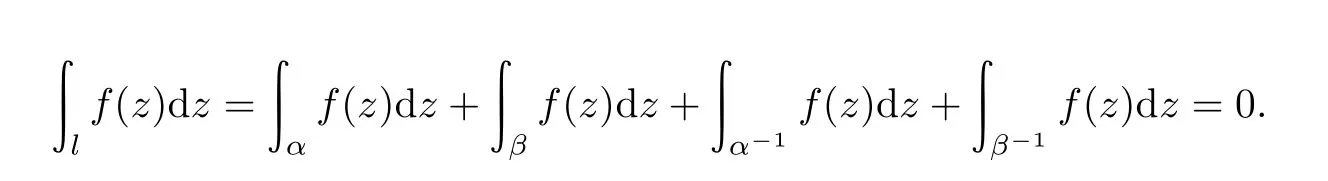
所以对于π1(D,p0)的全体换位子所生成的子群D′,及[β]=[γ][γ′][γ]−1[γ′]−1∈D′,有
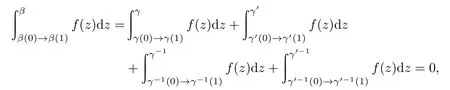
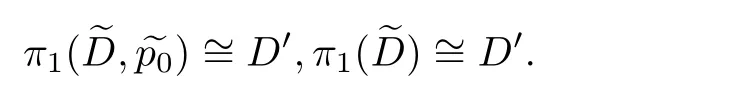
D′是π1(D)的子群,由引理1.1知

故Γ∼=N(D′)/D′.由于D′是π1(D)的全体换位子所生成的群,故N(D′)/D′是交换群并且是有限生成的,而有限生成交换群同构于有限个循环群的直和.事实上,覆盖变换群是由底曲面上一点的所有上方点之间的变换所构成的,那么对于任意
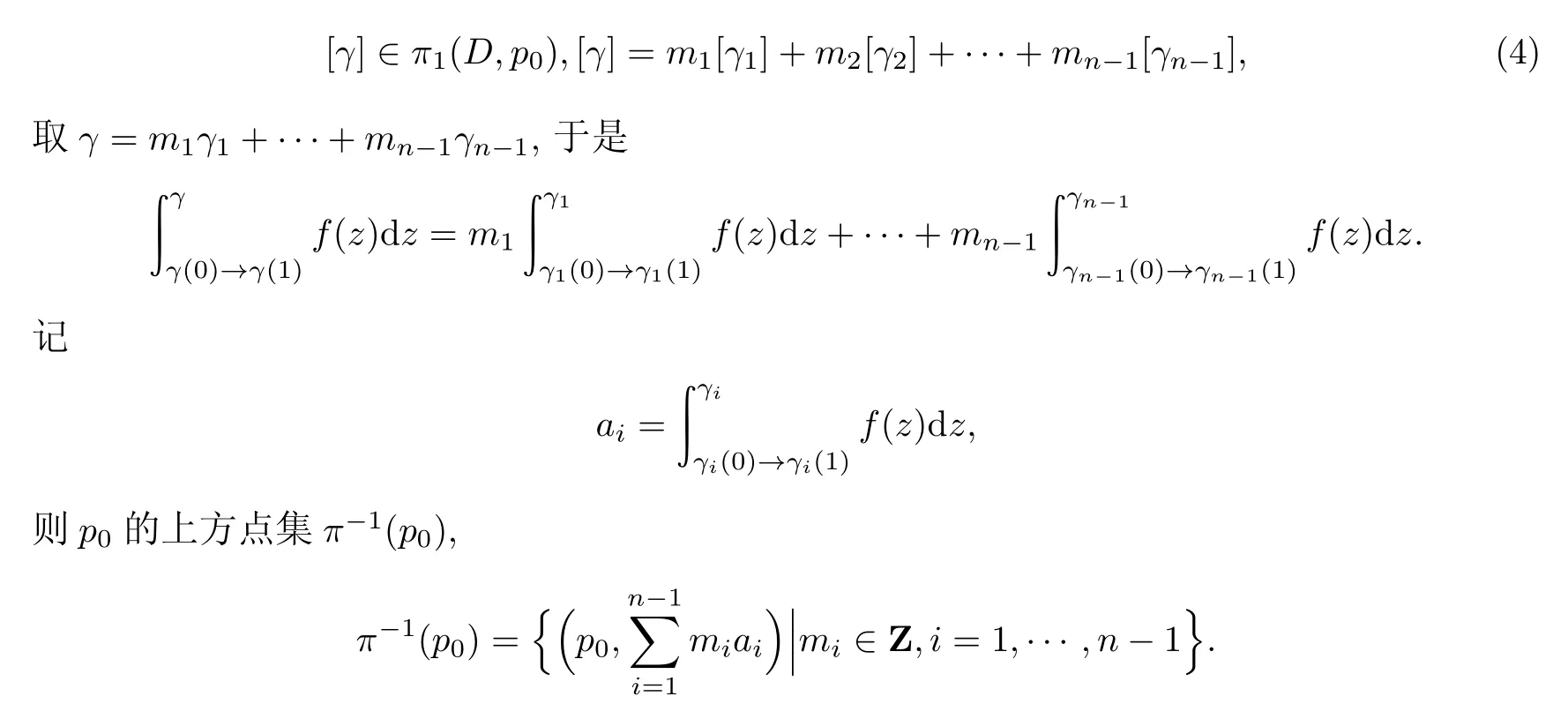
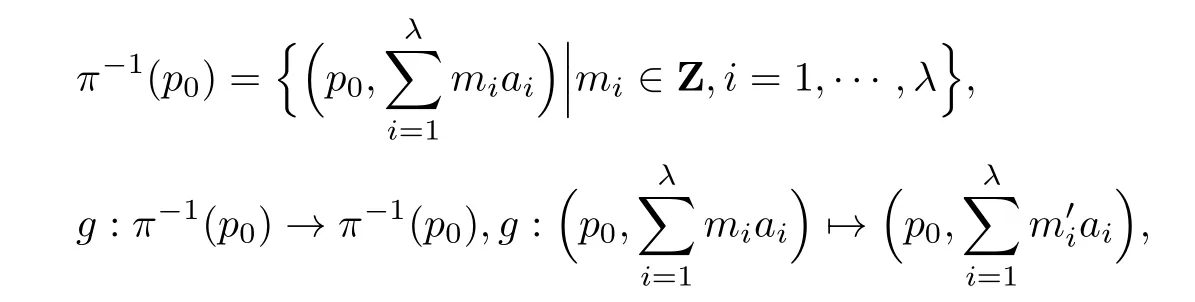
这样我们得到Γ∼=Z⊕Z⊕···⊕Z,Z的个数为λ.事实上,令
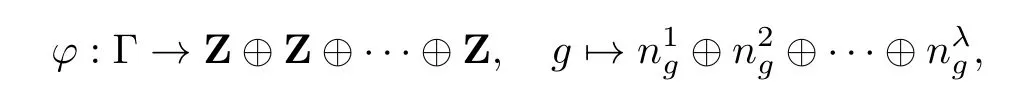
(i)φ是单同态.因为
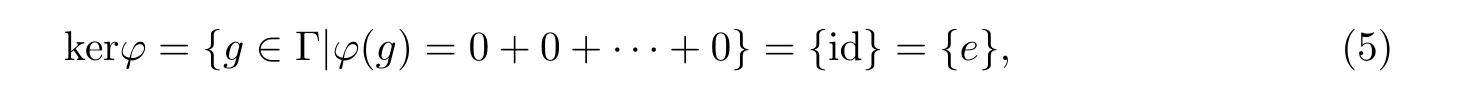
所以φ是单同态.
(ii)φ是满同态是显然的.
综上可知
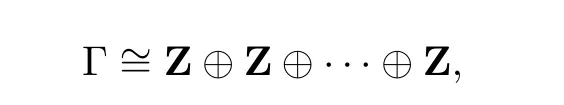
Z的个数由f(z)在γi上的积分不为0的个数决定.
推论的证明由于

Z的个数由f(z)在γi上的积分不为0的个数决定,又由于共有k个不为0,则由上面定理可知F(z)=f(ζ)dζ的一个单值分支的表达式为
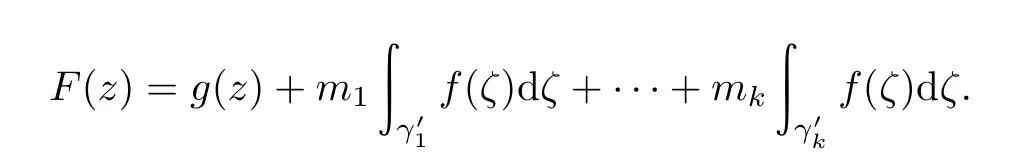
例子的证明(1)若f(z)恰当,则由定理2可知Γ={id},有序偶对为=所形成的黎曼曲面与D∗共形.
(2)若f(z)不是恰当的,由上述定理可知Γ∼=Z,则有序偶对为=(p,f(z)d z)所形成的黎曼曲面的基本群是{id},那么是单连通区域,由黎曼映射定理可知,与单位圆盘共形.
[1]吕以辇,张学莲.黎曼曲面[M].北京:科学出版社,1997.
[2]聂灵沼,丁石孙.代数学引论[M].北京:高等教育出版社,2010.
[3]熊金城.点集拓扑讲义[M].北京:高等教育出版社,2003.
[4]余家荣.复变函数[M].北京:高等教育出版社,2007.
(责任编辑:林磊)
Application of the covering space in the complex integral of multiply connected domains
HU Guang-ming1,LONG Jian-ren2
(1.School of Mathematics and Systems Science,Beihang University,Beijing 100191,China; 2.School of Mathematical Science,Guizhou Normal University,Guiyang 550001,China)
It is wellknown that the integralwith variable upper limit ofanalytic function is a single value function in the simple connected domain,while the integralwith variable upper limit of analytic function in the multiply connected domains is as following:F(z)=∫f(ζ)dζ,F(z)is not only dependent on the z(z0is the fixed point in D), but also depends on the integral path and function f(z)being exact or not in every hole. Therefore F(z)is likely to be multiple valued function.In this paper,we give a new proof method about the integral of analytic function f(z)in the multiply connected domain by the regular covering surface.
multiply connected domains;regular covering surface;group of covering transformations;exact diff erential;Abelian group
O174.5
A
10.3969/j.issn.1000-5641.2017.04.006
1000-5641(2017)04-0064-07
2016-11-27
贵州省科学技术基金(黔科合J字[2015]2112号);国家自然科学基金(11501142)
胡光明,男,博士研究生,研究方向为复分析及Teichm¨uller空间. E-mail:1186529024@qq.com.
龙见仁,男,教授,研究方向为复分析.E-mail:longjianren2004@163.com.

