Dougall5F4求和公式的一些应用

阮玉盛

(华东师范大学数学系,上海200241)

Dougall5F4求和公式的一些应用

阮玉盛

(华东师范大学数学系,上海200241)

Dougall5F4求和公式是特殊函数论中一个重要的级数求和公式,其在不同领域中的应用已被人们广泛讨论.本文以该公式为基础导出了一些新的求和公式,并利用这些公式给出了一系列新的关于1/π和1/π2的Ramanujan型级数公式.

伽马函数;超几何函数;Dougall5F4求和;Ramanujan型级数

0 引言

在文献[1]中,Ramanujan共提出了17个关于1/π的级数.1987年之前,仍然没有数学家可以真正处理这些级数.Borwein兄弟在文献[2]中第一次给出了Ramanujan级数的严格证明并得到了许多新的关于1/π的Ramanujan型级数.Chudnovsky兄弟则在文献[3]中给出了这些级数的一些拓展公式.

目前,有关1/π的一些新的Ramanujan型级数已经被许多数学家研究并取得了大量的成果,具体可参考文献[4-19].在文献[20]的基础上,本文通过对Dougall5F4求和公式中所包含的参数进行求导运算来得到一些新的有关1/π的Ramanujan型级数.同时,文章中还得到了许多新的关于其他常数的Ramanujan型级数.

本文需要下列有关特殊函数的一些基本概念.

定义0.1[21]对任意的复数z0,−1,−2,···,伽马函数Γ(z)可以定义为

其中(z)k为Pochhammer符号.

定义0.2若z为复数且n为自然数,则通常的Pochhammer符号被定义为

一般地,对于任意的复数α,可定义Pochhammer符号(z)α为

命题0.1[21]

式(3)中,γ代表欧拉常数,其具体定义为

命题0.2[21](欧拉反射公式)

定义0.3双伽马函数ψ(z)定义为

命题0.3[21]双伽马函数ψ(z)有如下性质.

其中0＜p＜q;∑′表示当q是偶数时,指标为n=q/2的项要除以2.这里,「q/2」表示不大于q/2的最大整数.

公式(7)也可以表达为

命题0.4[20](Dougall5F4公式)若R(a+b+c+d+1)＞0,则

命题0.5[20]若R(a+b+c+d+α−β−γ−δ+1)＞0,则

1 Dougall5F4求和公式的推广以及1/π的Ramanujan型级数

引理1.1对于任意的复数x,y,我们有

证明直接利用式(2)和定义0.1便可证明该引理.

定理1.1若R(a+b+c+d+1)＞0,则

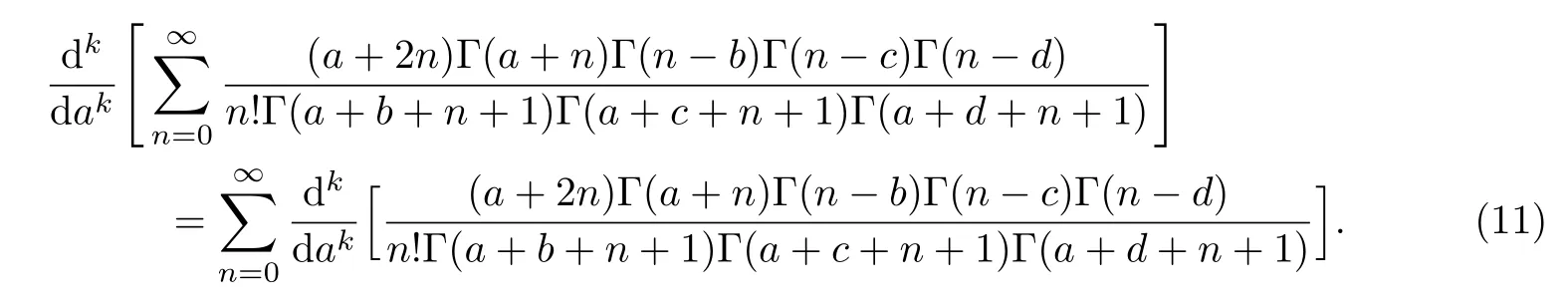
证明显然,上式左边被求导的级数是绝对收敛的.接下来我们需要证明此级数也是一致收敛的.记

利用引理1.1,我们有

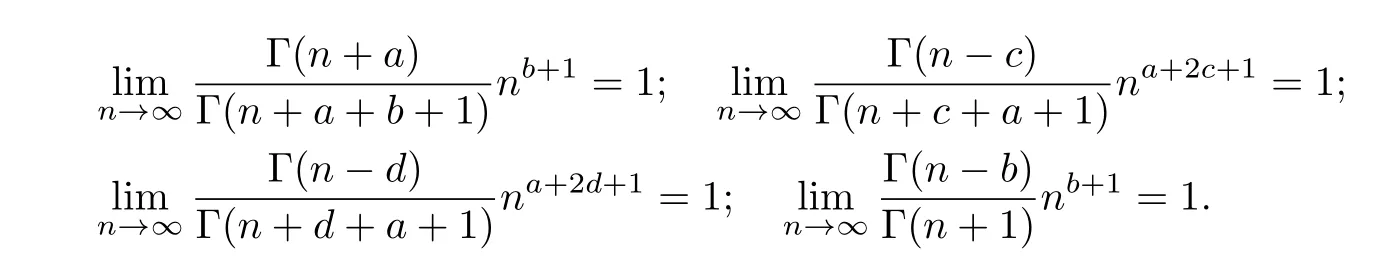
因此,当n→∞时,

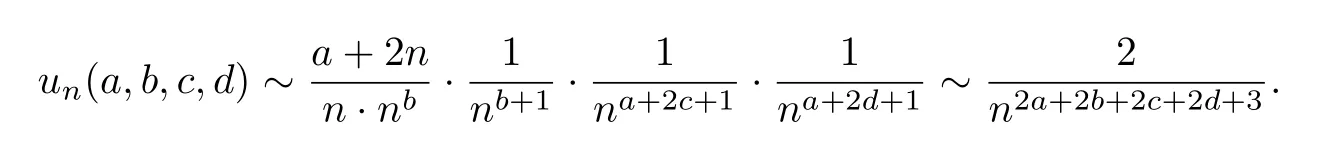
又由于R(2a+2b+2c+2d+3)＞1,故此级数一致收敛.

定义1.1设a,b,c,d为复数,n为整数.我们定义

其中ψ是由式(5)定义的双伽马函数.

定理1.2若R(a+b+c+d+1)＞0,则

证明首先,我们有

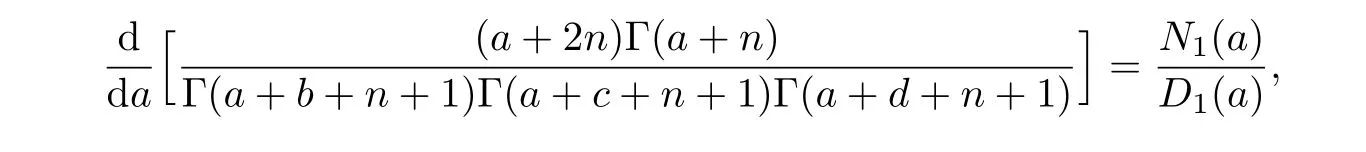
其中

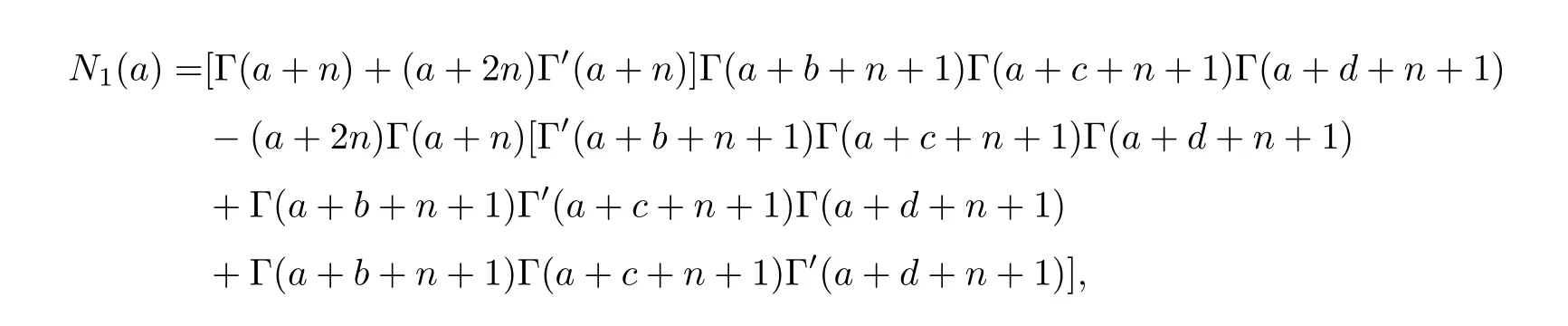
而

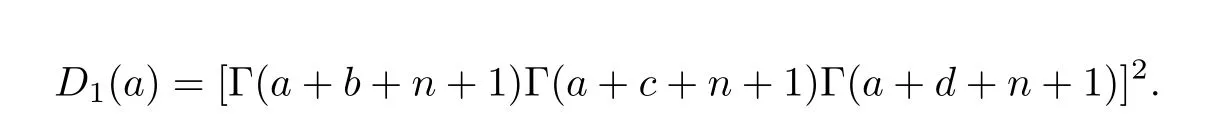
因此

另一方面

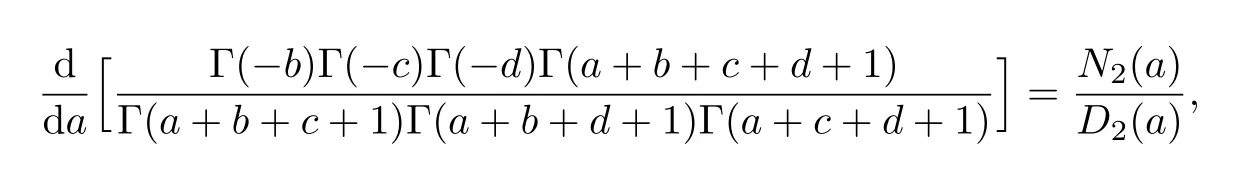
其中

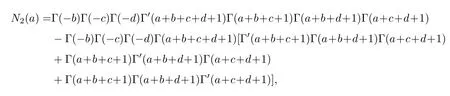
而

根据N2(a)和D2(a)的表达式,可进一步得到

最终,结合公式(9)、(11)、(13)以及(14),我们完成了公式(12)的证明.

定理1.3若R(a+b+c+d+α−β−γ−δ+1)＞0,则

证明利用公式(2),并将式(12)中的(a,b,c,d)替换为(a+α,b−β,c−γ,d−δ),就完成了定理的证明.

定理1.4若R(a+b+c+d)＞0,则

由于

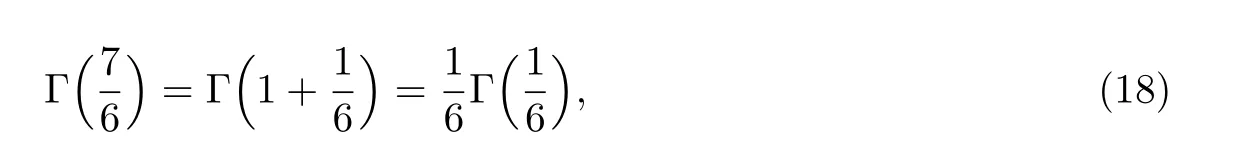
利用欧拉反射公式(4),我们有

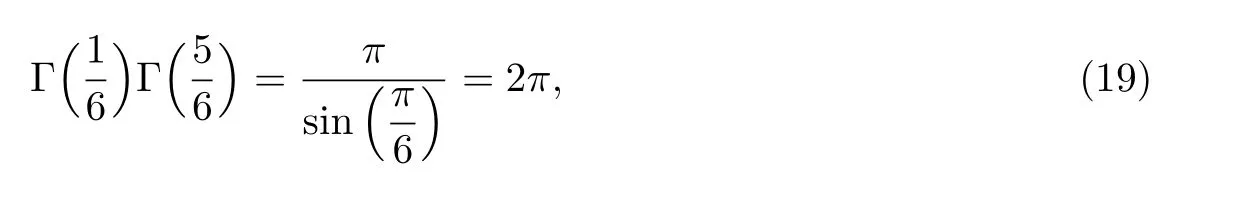
以及

在等式(17)的两边同时乘以2且将式(18)—(20)代入到此公式,我们就得到了公式(16).

例1在定理1.4中,取(a,b,c,d)=(1,0,0,0),则有

例2在定理1.4中令(a,b,c,d)=(1,−1,1,0),可以得出

2 π2的一般级数展开式

在这一节中,我们利用定理1.3来证明下面的级数展开式.

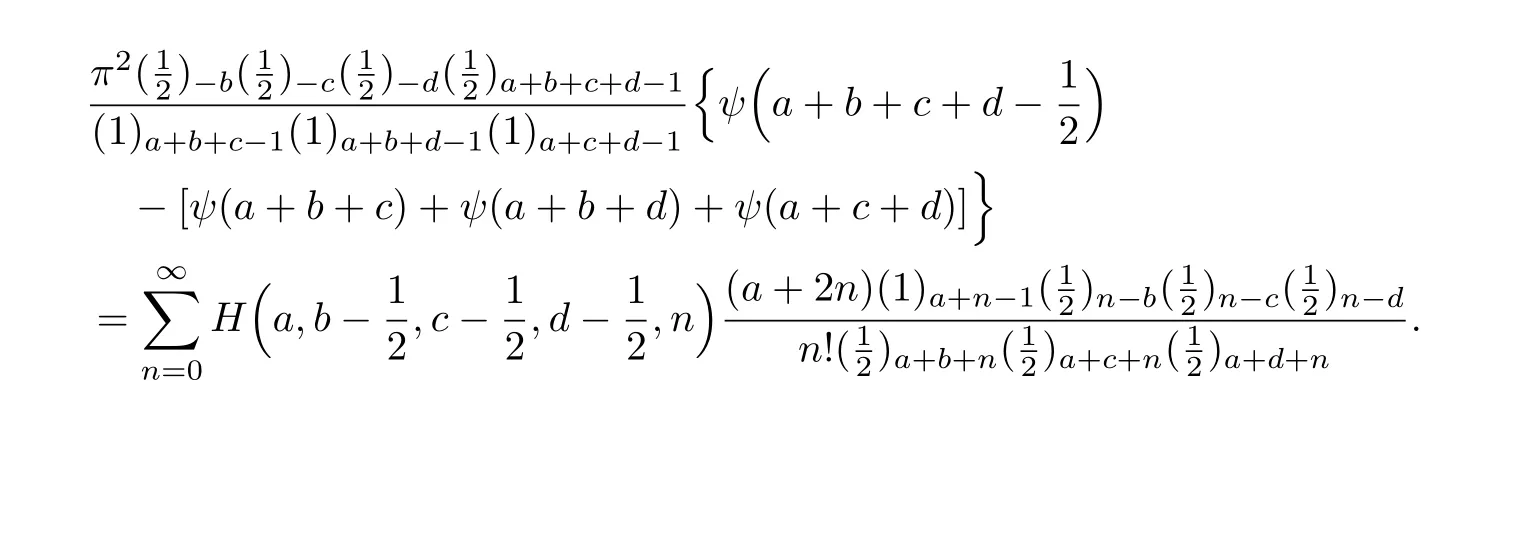
证明利用递归关系式Γ(z+1)=zΓ(z),我们可将定理1.3中的(15)式表示为

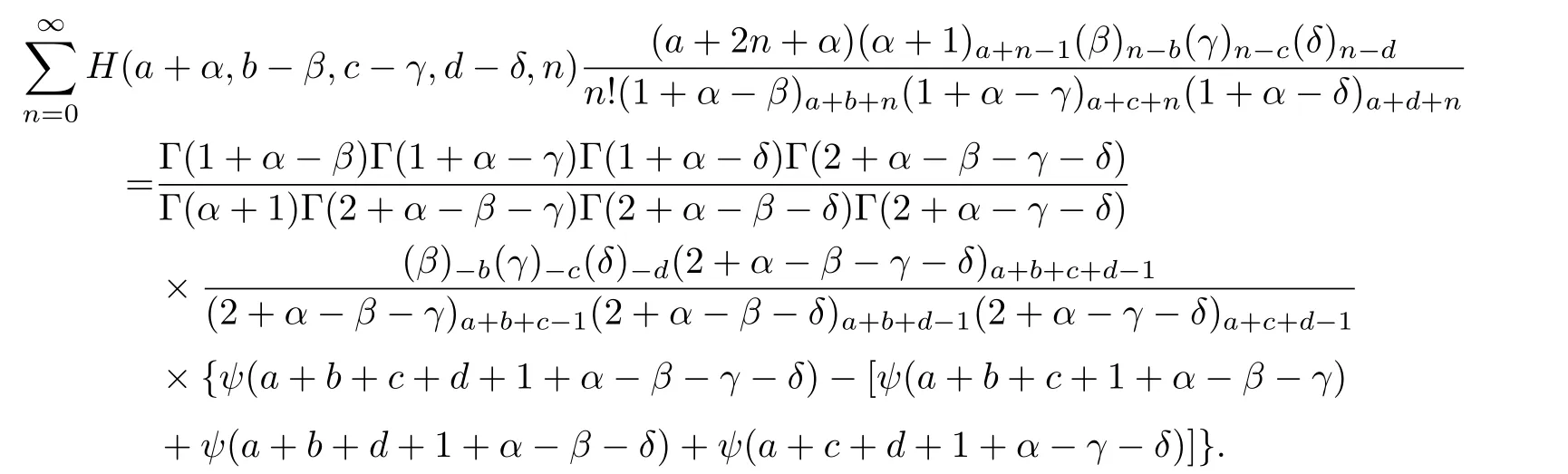
例3在定理2.1中,令(a,b,c,d)=(1,0,0,0),则有

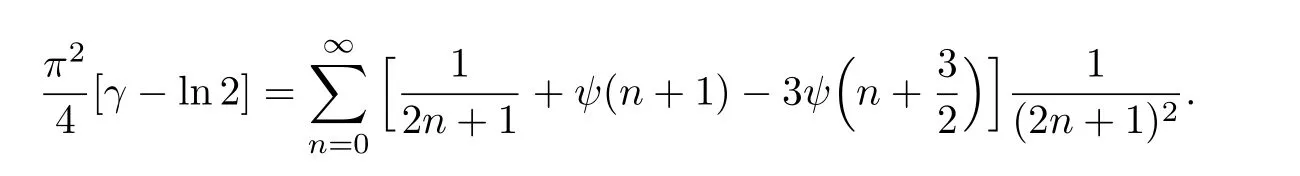
例4在定理2.1中,取(a,b,c,d)=(1,1,0,0),则有

例5在定理2.1中,令(a,b,c,d)=(2,−1,0,0),则可得

3 Γ-3()的一般级数展开式

例6在定理3.1中令(a,b,c,d)=(0,0,0,0),我们可推出

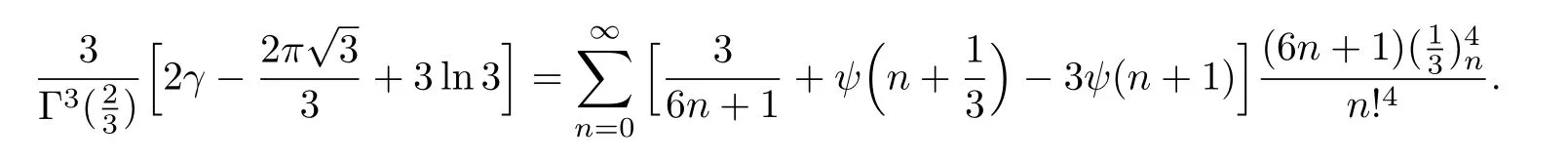
例7在定理3.1中令(a,b,c,d)=(1,0,0,0),我们可得到结论

例8在定理3.1中选取(a,b,c,d)=(1,−1,0,0),我们可得到

例9在定理4.1中令a=b=c=d=0,则有

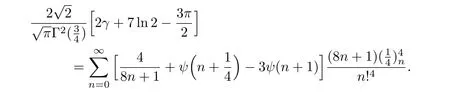
例10定理4.1中令a=1且b=c=d=0,则有

5 1/π2的Ramanujan型级数

定理5.1若R(a+b+c+d)＞0,则有

若在定理5.1中令b=c=d=−a,则可得到以下推论.

推论5.1若R(a)＜0,则

例11在推论5.1中令a=−1,则

例12在推论5.1中令a=−2,则

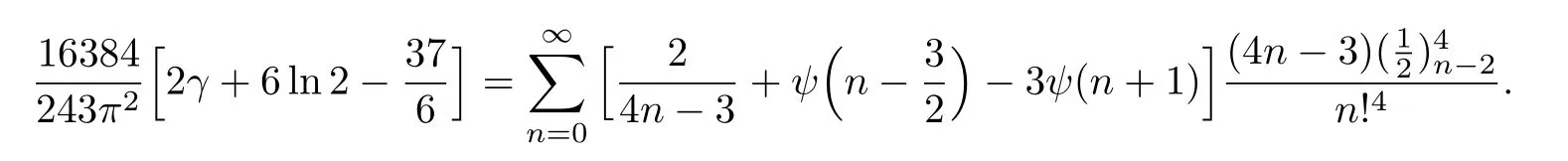
下面,我们将继续讨论定理5.1的特殊情形.在定理5.1中,若我们选取(a,b,c,d)= (k,0,0,0)并将其简化,我们很容易得到下面的命题.

命题5.1若k是正整数,则我们有

例13当k=1时,我们可以得到

命题5.2若k是一个非负整数,则我们有以下公式

证明在定理5.1中令(a,b,c,d)=(k,1,0,0)即可得到上面的等式.

例14在命题5.2中令k=0,我们可得到

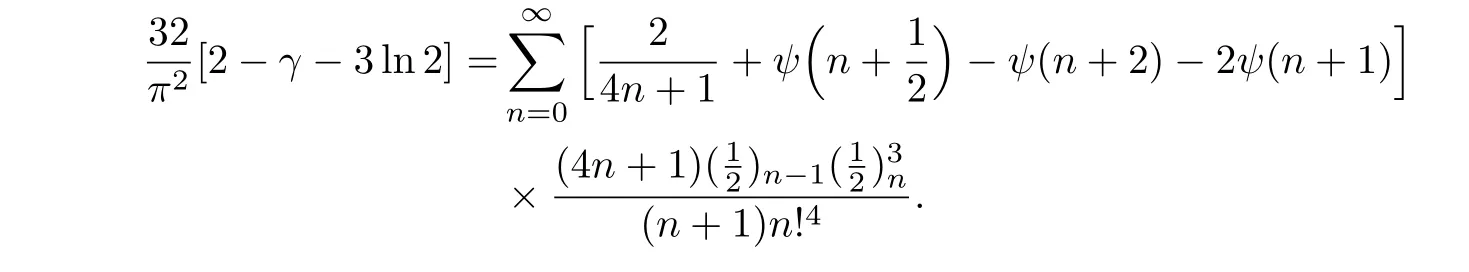
例15在命题5.2中取k=1,我们可推出

在定理5.1中选取(a,b,c,d)=(k,1,1,0),我们有以下等式

因此我们可得到下面的命题.

命题5.3若k≥0是整数,则我们有以下公式

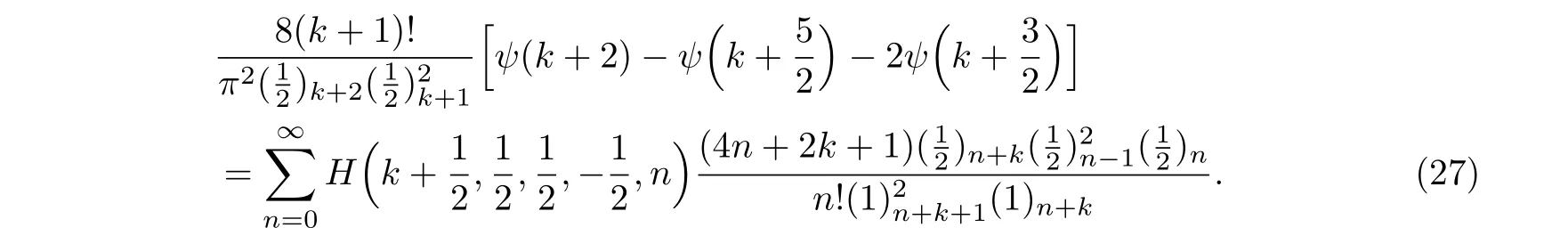
例16在式(27)中令k=0,我们可以得到

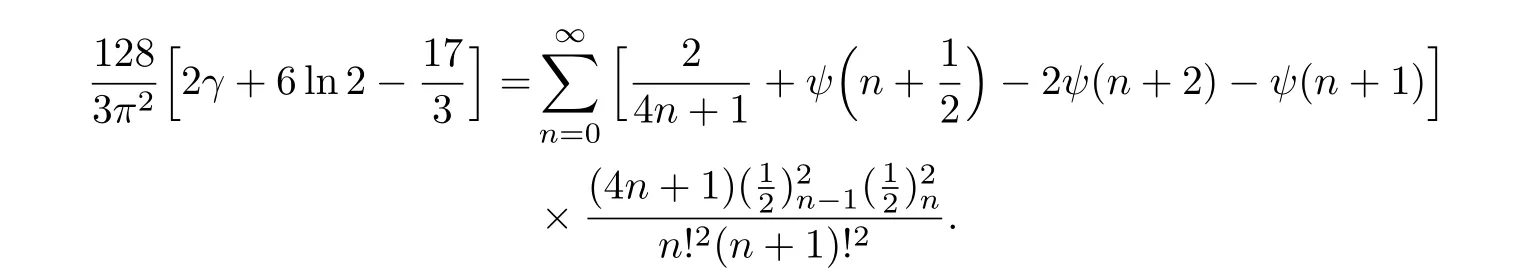
命题5.4若k是整数,且k≥−1,我们有

证明在定理5.1中取(a,b,c,d)=(k,1,1,1)即完成证明.

例17在式(28)中令k=−1,我们得到

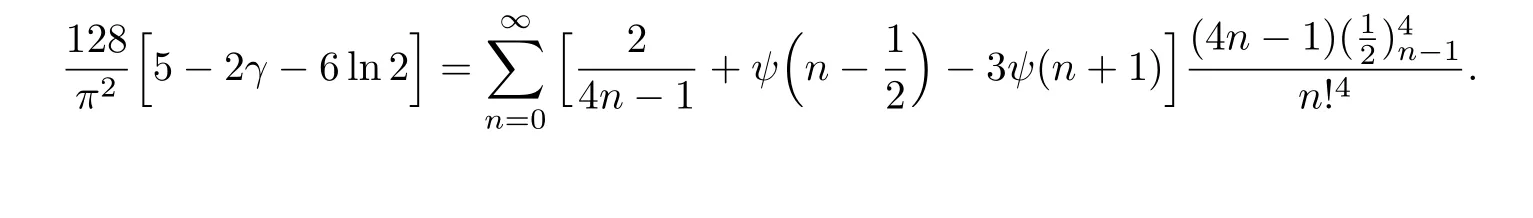
命题5.5若k是整数,且k≥2,我们有

证明在文[20]的定理7.1中取(a,b,c,d)=(k,−1,0,0).

例18在式(29)中令k=2,可得

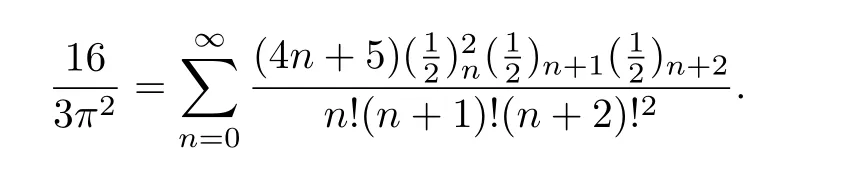
例19在式(29)中令k=3,可得

命题5.6若k是整数,且k≥3,我们有

证明在文[20]的定理7.1中令(a,b,c,d)=(k,−1,−1,0).

例20在式(30)中令k=3,可得

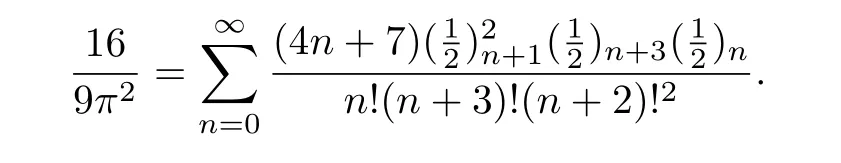
命题5.7若k是整数,且k≥−1,则

证明在文[20]的定理7.1中令(a,b,c,d)=(k,1,1,1).

例21在式(31)中取k=−1,可得

命题5.8若k是整数,且k≥2,则有

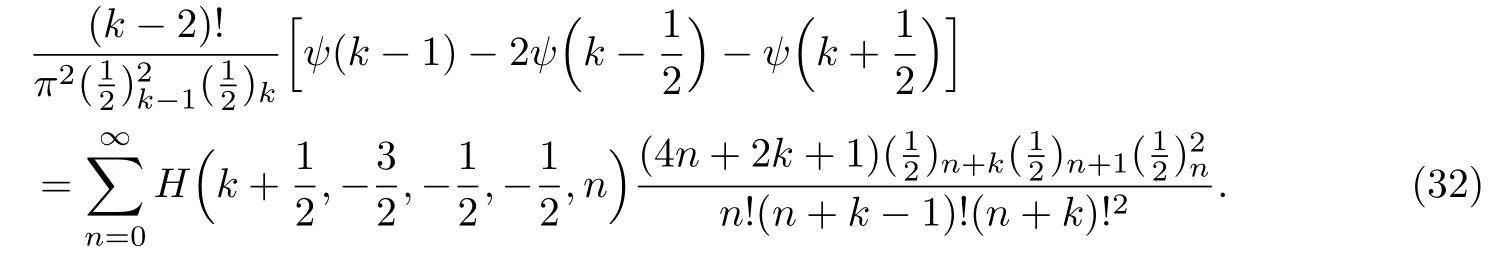
证明在定理5.1中令(a,b,c,d)=(k,−1,0,0)即完成证明.

例22在式(32)中取k=2,则有

命题5.9若k是整数,且k≥3,则

证明在定理5.1中令(a,b,c,d)=(k,−1,−1,0)即完成证明.

例23在式(33)中取k=3便可推出下列等式

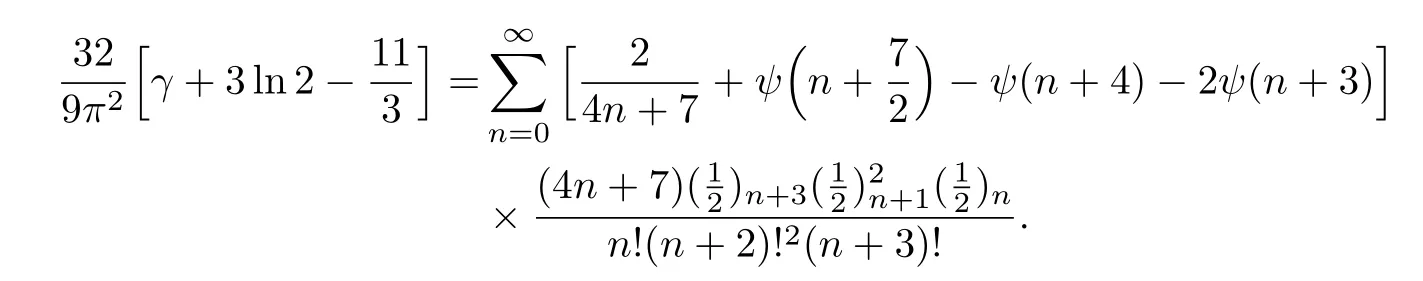
命题5.10若k是整数,且k≥4,则有

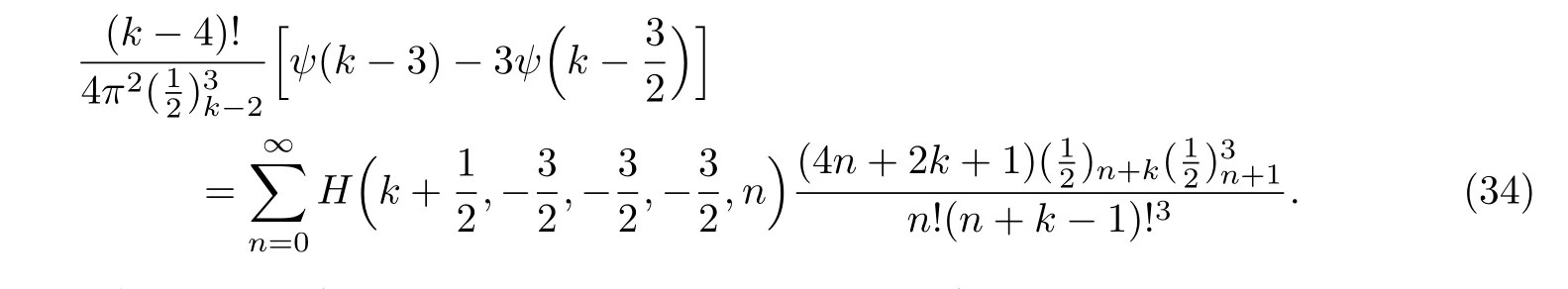
证明在定理5.1中取(a,b,c,d)=(k,−1,−1,−1)即完成证明.

例24在式(34)中令k=4,可推出以下等式

致谢这是作者在华东师范大学攻读博士学位期间所写的论文.非常感谢导师刘治国教授在此期间给予的无私帮助和细心指导.

[1]RAMANUJAN S.Modular equations and approximations toπ[J].Quart J Math Oxford Ser,1914,45(2): 350-372.

[2]BORWEIN J M,BORWEIN P B.Pi and the AGM:A Study in Analytic Number Theory and Computational Complexity[M].New York:Wiley,1987.

[3]CHUDNOVSKY D V,CHUDNOVSKY G V,Approximations and complex multiplication according to Ramanujan[C]//Proceedings of the Centenary Conference,Urbana-Champaign,1987.Boston:Academic Press,1988, 375-472.

[4]BARUAH N D,BERNDT B C.Ramanujan’s series for 1/πarising from his cubic and quartic theories of elliptic functions[J].J Math Anal Appl 2008,341:357-371.

[5]BARUAH N D,BERNDT B C.Eisenstein Series and Ramanujan-type series for 1/π[J].Ramanujan J,2010, 23:17-44.

[6]BARUAH N D,BERNDT B C,CHAN H H.Ramanujan’s series for 1/π:A survey[J].Amer Math Monthly, 2009,116:567-587.

[7]BARUAH N D,NAYAK N.New hypergeometric-like series for 1/π2,arising from Ramanujan’s theory of elliptic functions to alternative base 3[J].Trans Amer Math Soc,2011,363:887-900.

[8]CHAN H H,CHAN S H,LIU Z G.Domb’s numbers and Ramanujan-Sato type series for 1/π[J].Adv in Math, 2004,186:396-410.

[9]CHAN H H,COOPER S,LIAW WC.The Rogers-Ramanujan continued fraction and a quintic iteration for 1/π [J].Proc Amer Math Soc,2007,135(11):3417-3425.

[10]CHAN H H,LIAWW C,TAN V.Ramanujan’s class invariantλnand a new class of series for 1/π[J].J London Math Soc,2001,64(2):93-106.

[11]CHAN H H,LOO K L.Ramanujan’s cubic continued revisited[J].Acta Arith,2007,126:305-313.

[12]CHAN H H,VERRILL H.The Ap´ery numbers,the Almkvist-Zudilin numbers and new series for 1/π[J].Math Res Lett,2009,16:405-420.

[13]CHAN H H,RUDILIN W.New representations for Ap´ery-like sequences 1/π[J].Mathematika,2010,56:107-117.

[14]CHU W.Dougall’s bilateral2H2series and Ramanujan-likeπformulas[J].Math Comp,2011,80:2223-2251.

[15]COOPER S.Series and iterations for 1/π[J].Acta Arith,2010,141:33-58.

[16]GUILLERA J.Hypergeometric identities for 10 extended Ramanujan-type series[J].Ramanujan J,2008,15: 219-234.

[17]LEVRIE P.Using Fourier-Legendre expansions to derive series for 1/πand 1/π2[J].Ramanujan J,2010,22: 221-230.

[18]ROGERS M.New5F4hypergeometric transformations,three-variable Mahler measures and formulas for 1/π [J].Ramanujan J,2009,18:327-340.

[19]ZUDILIN W.More Ramanujan-type formulae for 1/π2[J].Russian Math Surveys,2007,62(3):634-636.

[20]LIU Z G.A summation formula and Ramanujan type series[J].J Math Anal App,2012,389:1059-1065.

[21]ANDREWS G E,ASKEY R,ROY R.Special Functions[M].Cambridge:Cambridge University Press,1999.

(责任编辑：林磊)

Some applications of Dougall’s5F4summation

NGUYEN Ngoc Thinh
(Department of Mathematics,East China Normal University,Shanghai 200241,China)

Dougall’s5F4summation formula plays an important role in the theory of special functions,and its various applications have been widely discussed.Using Dougall’s5F4summation formula,we derive some new summation formulas,from which new Ramanujan type series for 1/πand 1/π2are obtained.

gamma function;hypergeometric functions;Dougall’s5F4summation; Ramanujan type series

O156

A

10.3969/j.issn.1000-5641.2017.04.005

1000-5641(2017)04-0052-12

2016-10-19

国家自然科学基金(11571114)

阮玉盛,男,博士研究生,研究方向为特殊函数与数论.E-mail：thinhnn02@yahoo.com.