风力发电机高速级齿轮裂纹特性研究

陈长征，杨成龙，刘 杰，张 磊

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870；2.辽宁省振动噪声控制技术工程研究中心，辽宁 沈阳 110870)



风力发电机高速级齿轮裂纹特性研究

陈长征1，2，杨成龙1,2，刘 杰1，张 磊1,2

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870；2.辽宁省振动噪声控制技术工程研究中心，辽宁 沈阳 110870)

以风力发电机高速级齿轮为研究对象，基于有限元分析方法进行齿轮裂纹研究，考虑了裂纹深度和裂纹发生位置对接触情况和啮合刚度的影响。研究结果表明，随着齿轮裂纹的出现，轮齿以裂纹为界被分离成两部分，变形应力不连续；随着裂纹深度加深，分离现象越加明显；随着裂纹发生位置的不同，啮合过程中产生阶跃性突变现象；在各啮合区内，啮合刚度呈现不同的降低幅度，对齿轮裂纹故障的研究和预防轮齿断裂等严重事故发生具有一定意义。

风力发电机；齿轮裂纹；接触分析；啮合刚度

0 前言

轮齿在载荷作用下，其根部所产生的弯曲应力最大，且在齿根过渡圆角处有应力集中，同时齿轮在转动过程中使轮齿重复受载，在交变应力反复作用下，齿根处将产生疲劳裂纹，裂纹扩展导致轮齿弯曲疲劳折断，因此为了避免轮齿折断、齿面损伤以及塑性变形等因素引发的生产事故，对齿面的接触应力和齿轮时变啮合刚度等方面的强度分析非常重要，为研究齿轮裂纹故障和预防轮齿断裂等严重事故发生具有重要意义。近几年来国内外学者对齿轮裂纹故障和接触分析进行了许多研究。刘双等[1]通过改变齿轮轮缘厚度，研究此参数对齿轮裂纹扩展路径的影响。万志国等[2]对时变啮合刚度算法进行修正完善，并对齿根裂纹进行动力学建模，为齿根裂纹的故障机理、寿命预测及故障诊断奠定理论基础。Pandya等[3]基于有限元分析方法，分析了不同齿轮参数下直线裂纹和预估裂纹对齿轮啮合刚度的影响规律。Ignacio Gonzalez-Perez等[4]认为有限元法分析齿轮的最大接触应力以及应力分布等计算是非常有效的，为齿轮动力学计算啮合变形提供了较为方便的算法。Seok-Chul Hwang等[5]通过对直齿轮和螺旋齿轮各自配对齿轮的接触应力的研究，提出一对配合齿轮的接触应力比AGMA标准更严重。

基于风力发电机齿轮长期处在高转速、重载荷的环境下，其高速级从动轮转速最高，重复受载最多，易产生裂纹故障，并且很少有文献考虑裂纹参数和啮合位置对齿轮接触分析及啮合刚度的影响情况，故本文以风力发电机高速级从动轮为研究对象，通过ANSYS有限元分析软件，进行各种状况下的齿轮裂纹接触分析研究，并通过接触分析结果计算整理出齿轮啮合刚度曲线，为齿轮故障研究提供一些理论依据。

1 齿轮接触分析

1.1裂纹齿有限元网格模型建立

本文采用的直齿轮参数如表1所示。

表1 风力发电机高速级齿轮参数

材料参数：泊松比0.3，弹性模量 206 GPa，密度7 850 kg/m3。

裂纹参数：裂纹方向α=45°，裂纹深度q为2 mm、4 mm、6 mm。

裂纹尖端的应力和应变是奇异的，以1r变化，为了产生应力、应变的奇异性，裂纹尖端周围的网格单元应该是二次单元，在1/4点处有中节点，这些单元即为奇异单元。

1.2 齿轮接触分析模型建立

1.2.1 有限元接触模型建立

由于接触分析属于非线性分析计算量较大，为了减小计算时间，本文只采用四对齿轮进行接触分析，将扭矩转化为切向力均匀的施加在节点上，并不需要载荷移置，本文在主动轮内孔边界的所有节点上施加切向力来模拟转矩，切向力公式为

F=T1rd×n

(1)

式中，rd为主动轮轴径；T1为主动轮转矩；n为轴孔节点数。

由于含裂纹的齿在参与单齿啮合时，载荷全部由裂纹齿承担，裂纹的出现带给齿轮的影响最为明显，所以本文着重对裂纹齿参与的单齿啮合区接触分析情况进行研究。

1.2.2 齿轮接触赫兹理论

齿轮接触强度计算均以两轴线平行圆柱体对压的赫兹公式为基础，通过对原始赫兹公式加以变形及系数修正而获得的，基于赫兹理论，最大接触应力公式为[6]

σH=FnπL1R1+1R21-v21E1+1-v22E2

(2)

式中，v1、v2为两圆柱体材料泊松比；E1、E2为两圆柱体材料弹性模量；R1、R2为两圆柱体的曲率半径；L为接触线长度，对于齿轮来说是齿宽；Fn为齿轮法向载荷。

Fn=KT2z1/z2rccosα

(3)

式中，T2为从动轮转矩；K为载荷分配系数；α为压力角；z1、z2为主从动轮齿数；rc为接触点半径。

1.2.3 啮合刚度计算原理

针对单对齿轮啮合刚度，有公式[7]

k=Fnbδ

(4)

式中，b为轮齿齿宽；δ为接触面法向总变形。

当重合度大于1时，齿轮的综合啮合刚度就是同时参与啮合的各对齿轮刚度之和，根据接触分析所得的主动轮转角变形量，计算得到齿轮扭转啮合刚度，再将其转化成齿轮综合啮合刚度。齿轮扭矩刚度公式

kT=Tiδ/rbi=Fnrbiδ/rbi=bkr2bi

(5)

所以齿轮啮合刚度公式为

k=kTbr2bi

(6)

式中，Ti为主动轮扭矩；rbi为主动轮基圆半径。

2 接触结果和啮合刚度分析

2.1 齿根裂纹对齿轮接触及刚度影响

选取正常齿轮和齿根裂纹长度4 mm的齿轮进行接触分析对比，无裂纹从动轮和含齿根裂纹从动轮变形情况如图1和图2所示。

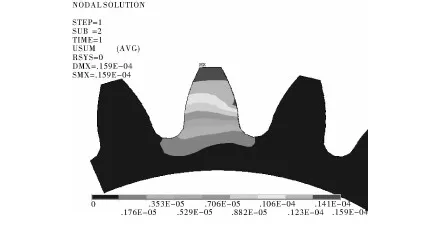
图1 正常齿轮接触变形

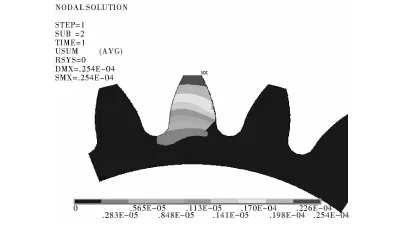
图2 齿根4 mm裂纹接触变形

通过图3和图4进行比较，可以看出变形最大值由0.159×10-4m增大到0.254×10-4m，增加了59.7%，齿轮的强度降低，齿轮变形量增大，并且轮齿的变形位置发生变化，轮齿变形以裂纹为界产生分离，接近齿顶部位即裂纹以上的部位发生变形，而裂纹以下的部位变形极小。

接触分析还需要进行应力比较，能够更清晰反映齿轮的受力情况，正常齿轮和齿根裂纹Von Mises应力情况如图3和图4所示。

随着裂纹的出现最大应力值由0.257×109Pa增加到0.293×109Pa，增加了14%，裂纹尖端出现应力集中现象，在裂纹尖端产生集中应力，使得裂纹迅速扩展，对齿轮的正常运转造成很大影响，严重缩短齿轮寿命。应力范围以裂纹为界产生分离现象，主要集中在接触区域、受压侧和齿根受拉侧，最大应力出现在接触区域，随着对接触区域的远离，应力逐渐变小，由于裂纹的出现受压一侧的应力区域变大，应力值变大，这对齿轮的产生很大损伤，加剧齿轮的损坏。

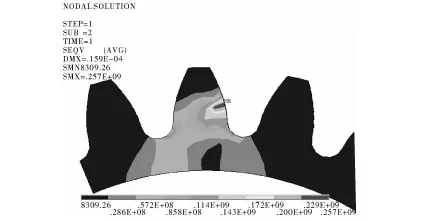
图3 正常齿轮Von Mises应力

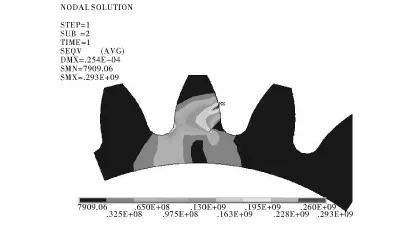
图4 齿根4 mm裂纹Von Mises应力

通过主动轮旋转一定角度，获得转角位移，重复以上操作，提取各啮合位置结果，经过计算并整理出齿轮时变啮合刚度，如图5所示。

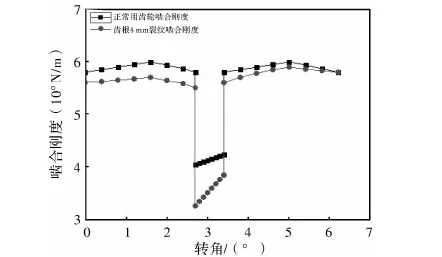
图5 齿轮时变啮合刚度

从图5可以看出，随着裂纹的出现，啮合刚度值减小，且降低率随着啮合过程的进行会产生不一样的趋势，降低率最高达到18%。从进入双齿区啮合到进入单齿区啮合区间，随着裂纹齿参与到啮合过程，裂纹齿承担的载荷逐渐增大，致使刚度降低率逐渐增大，啮合刚度降低的速度越来越快。当进入单齿啮合区间后，裂纹齿承担了所有载荷，刚度值会发生阶跃突变，降低率达到18%，刚度值最小值，在单齿啮合进行中，裂纹齿承担的载荷值保持不变，齿根部位承受的转矩会随着啮合位置发生变化，此次研究的是从动轮裂纹，啮合位置从齿顶到齿根的路径进行啮合，齿根裂纹承受的扭矩会越来越小，所以啮合刚度的降低率也会逐渐减小，在单齿啮合最高点处最大，即刚进入单齿啮合区位置。进入第二双齿啮合区，此次双齿啮合区与第一次相反，裂纹齿承担的载荷逐渐减小，降低率随之减小，啮合刚度值会慢慢趋向于正常齿轮啮合刚度值。

2.2 裂纹深度对齿轮接触及刚度影响

裂纹深度的变化使齿轮裂纹研究必须要考虑的因素之一，深度变化会对齿轮接触情况产生影响，不同深度的裂纹接触变形如图2、图6和图7所示。

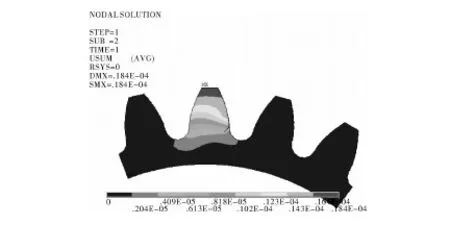
图6 齿根2 mm裂纹接触变形图

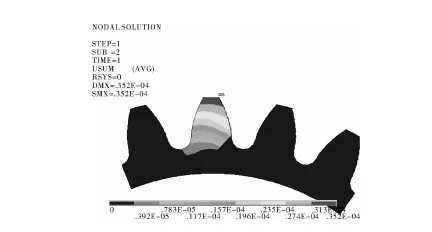
图7 齿根6 mm裂纹接触变形

随着裂纹深度的增加，对轮齿的强度影响越来越大，变形值的差别越来越明显，逐渐增大，达到3.52×10-4mm。随着裂纹深度的增加，变形分离现象越来越明显，对齿轮的接触区域轮齿体损伤越来越大，使得裂纹扩展更加迅速。

不同深度的裂纹接触Von Mises应力云图如图4、图8和图9所示。

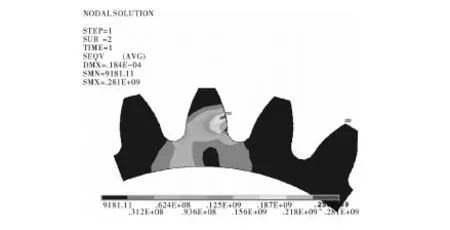
图8 齿根2 mm裂纹Von Mises应力

从应力最大值上可以看出，随着裂纹深度的增加，应力值呈现上升趋势，达到0.311×109Pa，裂纹尖端的应力集中现象越来越明显，受压一侧应力增大，逐渐超过接触区域应力值，范围也随之扩大，在运转中给予轮齿更大压力，加剧故障的发生。

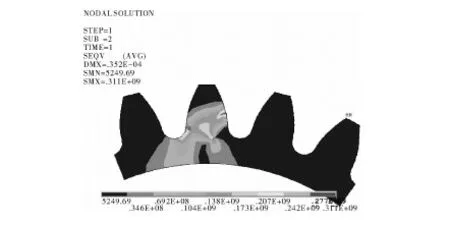
图9 齿根6 mm裂纹Von Mises应力

通过接触分析结果，计算并整理出不同深度裂纹对齿轮时变啮合刚度影响情况，如图10所示。

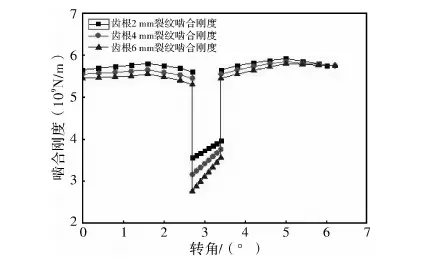
图10 齿根不同深度裂纹时变啮合刚度

随着裂纹深度的增加，对轮齿强度影响的更大，对啮合刚度的影响也会随之加深，数值会逐渐降低，增大了啮合刚度值的变化范围，使内部激励出现不等幅值。

2.3 裂纹位置对齿轮接触及刚度影响

在实际的齿轮运转状态中，裂纹不仅仅出现在轮齿齿根处。在轮齿表面上，分度圆处由于多次重复变载及受载较大，常常出现疲劳裂纹，随着这种裂纹的加深，轮齿容易出现半齿剥落现象。齿轮最常见的两个裂纹位置：齿根裂纹和分度圆裂纹，两种位置裂纹的接触变形如图2和图11所示。

由图11可以看出，由于分度圆裂纹存在，轮齿的最大变形位置发生改变，在啮合部位与裂纹以下的边界区域，沿着裂纹方向逐渐递减，轮齿的正常变形分布区域发生变化，主要在分度圆裂纹附近出现，这样会加剧裂纹的扩展，使齿轮损伤越来越严重。

图11 分度圆4 mm裂纹接触变形

分度圆裂纹和齿根裂纹接触Von Mises应力云图如图4和图12所示。

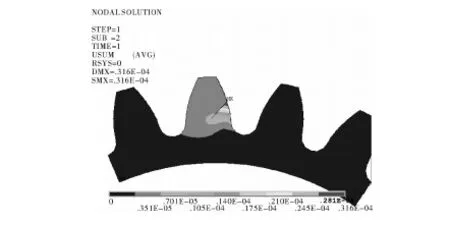
图12 分度圆4 mm裂纹Von Mises应力

通过图12可以看出，分度圆裂纹和齿根裂纹对接触应力的影响有很大区别，在此啮合位置上，分度圆裂纹应力最大值在裂纹前缘附近出现，由于啮合点离分度圆裂纹很近，更加促进了裂纹对轮齿的影响，在接近啮合点的裂纹前缘的应力集中现象最为明显。且在裂纹上方的轮齿接触应力值极小，完全由裂纹下方承载，这跟齿根裂纹出现的分离现象相同，只是啮合位置会随着齿轮的运转从裂纹以上到裂纹以下，这种情况会在过渡阶段出现突变，反复交替加剧轮齿的损坏速度。

通过接触分析结果计算整理出不同位置裂纹的齿轮时变啮合刚度如图13所示。

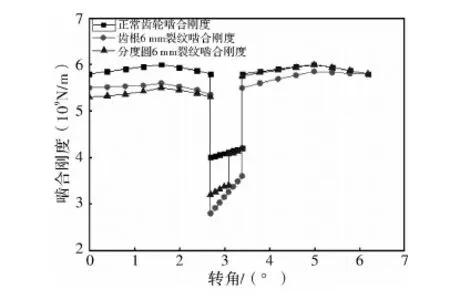
图13 不同位置裂纹时变啮合刚度

从图13可以看出不同裂纹位置对轮齿啮合刚度的影响有明显的差异性。在裂纹齿参与啮合的过程中，齿根裂纹对啮合刚度的影响是连续、完整的，刚度值会持续性发生变化；而分度圆裂纹对啮合刚度产生影响与否更加依赖于其啮合位置的变化，只有在分度圆裂纹处到齿顶之间部位参与啮合时，裂纹才会对啮合刚度产生明显影响，所以对于分度圆裂纹来说，在啮合位置由裂纹到齿顶区间过渡到裂纹到齿根区间时，啮合刚度会有阶跃性突变现象发生，不同于齿根裂纹的连续性影响。裂纹对刚度影响的实质是对轮齿体横载面及惯性矩的影响，所以对于分度圆裂纹来说，由于其对轮齿截面的影响是突变性的，这就导致啮合刚度产生阶跃性突变。在单齿啮合区中，随着啮合传动进行，啮合位置处于分度圆裂纹到齿根区间时，裂纹对啮合刚度的影响极小，趋于正常齿轮的啮合刚度值，一直延续到裂纹齿参与啮合结束。

3 结束语

针对齿轮裂纹的各种情况进行接触分析，得出齿轮特性的一般规律：

(1)齿轮裂纹会对齿轮正常啮合接触的变形值和应力值产生影响，使得数值都有增大趋势，裂纹前缘出现应力集中现象，并且齿轮以裂纹为界发生分离现象，裂纹上下部位表现出两种不同的分析结果，啮合刚度在不同啮合位置呈现不同的降低率。

(2)随着裂纹深度的增加，对轮齿的强度影响越来越大，数值增大，齿轮被裂纹分离现象更加明显，受压一侧的应力逐渐加剧，分布区域也随之扩大，啮合刚度值整体呈现降低趋势。

(3)不同位置的裂纹，对齿轮的接触呈现不同的影响情况，主要取决于啮合位置相对于裂纹位置之间的距离，分度圆裂纹时变啮合刚度随着啮合位置的改变出现阶跃性突变。

这些结果显示出齿轮在正常运行中裂纹对齿轮特性的一些改变，裂纹一旦出现，扩展速度变快，直至轮齿折断，造成重大危害，本文为达到齿轮能够高速平稳运转的目标提供一些依据，对齿轮裂纹故障的研究，预防轮齿断裂等严重事故发生具有一定意义。

[1] 刘双,朱如鹏,陆凤霞.齿轮轮缘厚度对裂纹,扩展路径的影响研究[J].机械制造与自动化,2013,42(6):11-14.

[2] 万志国,訾艳阳,曹洪瑞,等.时变啮合刚度算法修正与齿根裂纹动力学建模[J].机械工程学报,2013,49(11):153-160.

[3] Pandya Y, Parey A.Simulation of Crack Propagation in Spur Gear tooth crack and its influence on Mesh Stiffness [J].Engineering Failure Analysis,2013,30(5): 124-137.

[4] Ignacio Gonzalez-Perez, Jose L. Iserte. Alfonso Fuentes Implementation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact[J].Mechanism and Machine Theory ,2011,46(6):765-783.

[5] Seok-Chul Hwang, Jin-Hwan Lee.Contact stress analysis for a pair of mating gears[J].Mathematical and computer modeling, 2013,57(1):40-49.

[6] 李特文.齿轮啮合原理(二版)[M].上海:上海科学技术山版社,2004.

[7] 张素燕.考虑齿顶修缘的直齿轮-转子系统非线性动力学特性研究[D]．沈阳：东北大学，2015．

Study on crack characteristics of high speed gear for wind turbine generator

CHEN Chang-zheng1,2，YANG Cheng-long1,2，LIU Jie1，ZNANG Lei1,2

(1.School of Mechanical，Shenyang University of Technology，Shenyang 110870，China； 2.Liaoning Engineering Center for Vibration and Noise Control，Shenyang 110870，China)

The high speed gear of wind turbine generator is as the research object, this paper researches on gear crack based on finite element analysis method, and the effects of crack depth and crack location on the contact and meshing stiffness. The test result indicated that with the occurrence of crack gear, the crack serves as the boundary the tooth was divided into two parts, and the deformation stress was discontinuity. With the deepening of the crack depth, the divides was more obvious. With the different of the crack locations, the step mutation may come during meshing process, in each of the meshing regions, the meshing stiffness shows the different lowering rate. It is some significance for the research of the gear crack fault and prevention of tooth fracture and other serious accidents.

wind turbine;gear crack;contact analysis;meshing stiffness

2016-12-14；

2017-03-15

国家自然科学基金(51305276) 辽宁省教育厅项目(L2014039)

陈长征(1964-)，男，博士，教授，博士生导师。

TM315

A

1001-196X(2017)04-0056-06