带有库存限制与需求更新的供应链订货策略研究
温 馨,郭永江
(北京邮电大学理学院,北京 100876)
带有库存限制与需求更新的供应链订货策略研究
温 馨,郭永江
(北京邮电大学理学院,北京 100876)
针对季节性产品的销售,研究了带有库存限制与需求更新的供应链的订货策略问题。该问题中供应链由一个供应商与一个零售商构成,假设零售商有两次订货机会,分别发生在得到需求信号前后,且第一次订货受到了零售商库存的限制。对于该问题,首先利用导数的性质和逆推的方法,通过参数指标设置求解出无库存限制时的最优订货策略,再利用凹函数的性质得到在不同情况下有库存限制时的最优订货策略,使得供应链能够协调。最后通过算例验证了结果的正确性,并对最优的订货策略作了进一步解释。
库存限制;需求信号;供应链;回购合同
随着经济发展,企业间经济联系越来越紧密,企业所处的供应链关系着企业的生存发展。一个风险程度低、反应速度快、协调性高的供应链可以使企业在市场竞争中处于有利位置。基于对期望收益的最大化以及合同的协调性等指标的考量,采用各种数学方法对供应链结构进行计算和评价,是供应链管理领域非常重要的研究内容。
经典的供应链管理问题不考虑零售商的库存问题,但事实上零售商的库存是有限的,很多学者研究了有库存限制的供应链模型。Pasternack[1]研究了有库存限制的报童模型,利用收益共享合同来分配利润;Lim等[2]提出了零售商批发季节性产品且有库存限制的问题,在这个问题中零售商只有一次订货机会,并利用收益共享合同协调了供应链。经典的供应链问题不考虑第二次订货的问题,但事实上零售商根据市场情况进行再次订货也是合理的。Fisher等[3]提出零售商的需求更新可能改善整个供应链;Donohue[4]提出了零售商在出售季之前得到需求信号并进行第二次订货的模型;李健等[5]研究了带有需求更新的两阶段电子商务供应链模型,并设计了订购合同使供应链协调。简惠云等[6]研究了一般的二阶段并带有需求更新的供应链模型。胡觉亮等[7]和尚文芳等[8]分别研究了二阶段带有需求更新的服装供应链模型和延期供给的易逝品供应链模型。宋华明等[9]研究了带有需求更新的供应链的合作问题,并论证了合作策略的必要性。
在回购合同(buy-back contract)中,零售商在出售季之前以一个固定的批发价向供应商订购产品,出售季之后,如果零售商有剩余产品,供应商再以一个固定的回购价格回购这些产品。对于回购合同,Pasternack[10]针对报童问题对回购合同进行了详细分析,并指出回购合同能够协调供应链。邓欣[11]利用回购合同研究了损失厌恶偏好的供应链模型。在回购合同中,供应商会回购零售商的剩余产品,这样可能导致零售商的不理性订货,Porteus[12]的研究表明,零售商的不理性订货是不稳定的。Padmanabhan等[13]研究了一个供应商利用回购合同来处理多个零售商之间竞争的问题。除了回购合同之外,还有一些其它的合同也可以用于利润的分配,如批发价合同、收益共享合同、数量柔性合同以及销售回扣合同等。Lariviere等[14]在报童模型下对批发价合同进行了全面分析,Cachon等[15]在一般情况下对收益共享合同提供了一个完整的分析,Tsay[16]研究了利用数量柔性合同进行协调的供应链,Taylor[17]研究了利用销售回扣合同进行协调的供应链。因为回购合同在实际中很普遍且一般情况下能协调供应链,故本文也采用了回购合同。
本文针对季节性产品的销售,研究了零售商带有库存限制且有两次订货机会的供应链的订货策略,零售商的两次订货分别发生在得到需求信号前后,零售商的第一次订货受到库存的限制,在进行第二次订货时对市场需求有了更进一步了解,供应商直接发货给消费者,故第二次订货不受库存的限制。第二次订货对总的订货量进行了调整使得利润尽可能增大。本文利用回购合同进行利润分配,首先通过数学推导和参数设置,利用导数的性质和逆推的方法,求解出无库存限制时的最优订货策略,然后再利用分类讨论的方法和凹函数的性质得到有库存限制时不同情况下最优的订货策略。该供应链模型在实际中很常见,为了更好地利用本文所得的最优订货策略,本文给出了相应的实例。
一、带有库存限制与需求更新的供应链模型
本文研究零售商有库存限制且有两次订货机会的供应链模型:一个供应商和一个有库存限制的零售商,单一的出售季与随机需求。零售商在出售季之前有一次得到需求信号的机会,在出售季之前零售商有两次机会向供应商订货,第一次订货发生在得到需求信号之前,第二次订货发生在得到需求信号之后。为了方便,本文把整个过程分为两个阶段,第一阶段为得到需求信号之前,第二阶段为得到需求信号与出售季之间。第一阶段的订货选择源于市场需求分析与以往的经验且受制于零售商的有限库存。第二阶段的订货选择源于新得到的需求信号,零售商对所有的需求有了比较全面的了解。零售商第二次订货时,供应商生产产品并在出售季开始时直接发货给消费者,故零售商第二次订的产品并不占用零售商的库存。如果第一次订货量大于正常需求量,那么第二次订货就不会存在,即第二阶段的订货量为零,否则第二阶段还需要订货。
(一)符号定义与模型假设
V:零售商的库存容量;
v:单位产品所占的体积;
D:小范围内的市场需求;
ξ:得到的需求信号;
G(·):需求信号ξ的分布函数;
g(·):需求信号ξ的密度函数;
F(·|ξ):得到需求信号ξ之后,需求D的分布函数;
f(·|ξ):得到需求信号ξ之后,需求D的密度函数;
p:单位产品的零售价;
w1:第一阶段单位产品的批发价;
w2:第二阶段单位产品的批发价;
b:单位产品的回购价格;
c1:第一阶段单位产品的成本;
c2:第二阶段单位产品的成本;
q1:零售商在第一阶段的总订货量;
q2:整个过程中零售商的总订货量;
π2(q2|q1,ξ):给定q1与ξ,总订货量为q2时供应链的利润函数;
πr2(q2|q1,ξ):给定q1与ξ,总订货量为q2时零售商的利润函数;
πs2(q2|q1,ξ):给定q1与ξ,总订货量为q2时供应商的利润函数;
q2(q1,ξ):给定q1与ξ,使供应链利润最大的q2;
π1(q1):整个过程中,总订货量为q2(q1,ξ),第一阶段总订货量为q1时供应链的利润函数;
πr1(q1):整个过程中,总订货量为q2(q1,ξ),第一阶段总订货量为q1时零售商的利润函数;
πs1(q1):整个过程中,总订货量为q2(q1,ξ),第一阶段总订货量为q1时供应商的利润函数。
假设:供应商在每一阶段按零售商的订货量生产产品;F(·|ξ)严格单增,p为常数;产品的成本包括库存费用、运输费用以及生产费用等其他费用;出售季结束之后产品的剩余价值为零;需求信号ξ与需求D单位一样且ξ≥0;c1 (二)模型分析与求解 本节求解带有库存限制与需求更新的供应链的最优订货策略。首先考虑无库存限制的情况,利用逆推的方法找到第一、二阶段的最优订货量;然后考虑有库存限制的情况,利用凹函数的性质,得到带有库存限制与需求更新的供应链的最优订货策略。 得到需求信号ξ之后,需求D的分布函数为: F(x|ξ)=P(D≤x|ξ), 当需求信号ξ增大时,需求D增大,p(D≤x|ξ)减小,故F(x|ξ)随着ξ的增大而减小。 1.求解无库存限制时带有需求更新的供应链的最优订货策略 首先分析第二阶段,为了方便,把产品的售出及剩余产品的回购均看作是第二阶段发生的。第二阶段供应链的利润函数等于卖出去产品所得收益减去第二阶段的成本。给定q1与ξ,总订货量为q2时供应链的利润函数为: π2(q2|q1,ξ)=pS(q2|ξ)-c2(q2-q1)=pS(q2|ξ)-c2q2+c2q1, 其中: 此时, (1) q2(q1,ξ)=q1. 给定q1、ξ总订货量为q2时零售商的利润函数:πr2(q2|q1,ξ)=pS(q2|ξ)+b[q2-S(q2|ξ)]-w2(q2-q1) =(p-b)S(q2|ξ)-(w2-b)q2+w2q1. 给定q1、ξ总订货量为q2时供应商的利润函数: πs2(q2|q1,ξ)= w2(q2-q1)-c2(q2-q1)-b[q2-S(q2|ξ)]. 考虑回购参数{w2,b}引入常数λ≥0,使得: (2) 则λ∈(0,1),且 πr2(q2|q1,ξ)=λπ2(q2|q1,ξ)-λc2q1+w2q1, πs2(q2|q1,ξ)=(1-λ)π2(q2|q1,ξ)+λc2q1-w2q1, 故给定q1、ξ后,供应链、零售商和供应商最优总订货量均为q2(q1,ξ)。 下面分析整个供应链,把在第二阶段中找到的给定q1与ξ之后最优总订货量q2(q1,ξ)代入整个过程的供应链利润函数中,寻找最优的q1。 定义函数ξ(q1),使得: (3) 即给定一个q1就可以找到一个函数ξ(q1),当需求信号为ξ(q1)时,最优总订货量为: ξ(q1)恰好把需求信号划分成了两部分:当ξ>ξ(q1)时,第二阶段需要订货,此时 q2(q1,ξ)>q1, 且满足式(1)。此时q2(q1,ξ)与q1无关。当ξ≤ξ(q1)时,第二阶段不需要订货,此时 q2(q1,ξ)=q1. 供应链的利润函数等于卖出去产品所得的收益减去两个阶段的成本。整个过程中,总订货量为q2(q1,ξ),第一阶段订货量为q1时应链的利润函数: π1(q1)=E[π2(q2(q1,ξ)|q1,ξ)]-c1q1=pE[S(q2(q1,ξ)|ξ)]-c2E[q2(q1,ξ)]+ c2q1-c1q1. 定理1π1(q1)关于q1是凹函数。 证明:首先对π1(q1)求一阶导, S[q1|ξ(q1)]g[ξ(q1)ξ′(q1)- S[q2(q1,ξ(q1))|ξ(q1)]g[ξ(q1)]ξ′(q1) 其中q2[q1,ξ(q1)]=q1。 则 故π1(q1)是凹函数。□ (4) 整个过程中,总订货量为q2(q1,ξ),第一阶段订货量为q1时零售商的利润函数: πr1(q1)=E[πr2(q2(q1|ξ)|q1,ξ)]-w1q1=λE[π2(q2(q1,ξ)|q1,ξ)]-(w1-w2+λc2)q1. 整个过程中,总订货量为q2(q1,ξ),第一阶段订货量为q1时供应商的利润函数: πs1(q1)=E[πs2(q2(q1,ξ)|q1,ξ)]-c1q1+w1q1. 选择w1使得 w1-w2+λc2=λc1 (5) 则 πr1(q1)=λπ1(q1), πs1(q1)=(1-λ)π1(q1), 故供应链、零售商和供应商第一阶段的最优订货量均为q1*。 综上所述,在无库存限制时,第一、二阶段的最优订货量分别为q1*、q2(q1*,ξ)-q1*,总订货量为q2(q1*,ξ)。 2.求解带有库存限制与需求更新的供应链的最优订货策略 从第1节的分析中可知,在两个阶段中供应链最优的订货量均是零售商和供应商的最优订货量,且第二阶段和整个过程供应链利润函数均为凹函数。 零售商第一阶段的订货量受到库存的限制,第二阶段的订货量不受库存的限制,在第二阶段供应商生产产品并直接发货给消费者。 设 (6) (一)实例分析 考虑某种在单一季节出售的产品,并且假设小范围内需求的变动对市场价格无影响。单位产品所占体积: v=0.5m×0.5m×1.5m=0.375m3, 第一、二阶段产品的成本分别为c1=80元、c2=100元,产品的零售价p=200元,零售商的库存容量: V=10m×10m×3m=300m3, 假设需求信号ξ~U(800,1200),给定ξ之后,需求D~U(ξ-200,ξ+200),零售商和供应商通过协商决定各自利润占供应链利润的一半,即λ=0.5,则由式(2)得b=100元,w2=150元,再由式(5)得w1=140元,由式(6)可得: 由式(3) 得 故此时第二阶段的最优订货量为 总的最优订货量为 如果 V=10m×5m×3m=150m3, 其它量不变,则由式(6) 则 则此时第二阶段的最优订货量为 总的最优订货量为 如果在第二阶段开始时观察到的需求信号ξ=300,零售商的库存容量 V=10m×5m×3m=150m3, 其它量不变,则由式(6) (二)应用总结 本文针对季节性产品的销售,研究了带有库存限制与需求更新的供应链,该供应链利用回购合同进行利润分配,本文利用逆推的方法和凹函数的性质,通过参数设置,分别得到了不同情况下第一、二阶段的最优订货量,该最优订货量能够协调供应链且使得供应链、零售商和供应商利润均达到最大。在实际中也可以直接利用这个模型使得各自利润最大。为了进一步理解该模型及最优的订货策略,给出了相应的算例。本文只研究了一个供应商和一个带有库存限制的零售商的供应链,事实上一个供应商对多个带有库存限制的零售商的情况很普遍,零售商可以通过各种促销增加销售量,产品过了销售季还有剩余价值,批发价会随着订货量的变化而变化等,这些情况有待进一步研究。 [1] PASTERNACK B A. The capacitated newsboy problem with revenue sharing[J]. Journal of Applied Mathematics and Decision Sciences, 2001, 5(1):21-33. [2] LIM Y F , WANG Y Z, WU Y. Consignment contracts with revenue sharing for a capacitated retailer and multiple manufacturers[J]. Manufacturing & Service Operations Management, 2015, 17(4):527-537. [3] FISHER M, RAMAN A. Ruducing the cost of demand uncertainty through accurate response to early sales[J]. Operations Research, 1996, 44(1):87-99. [4] DONOHUE K L. Efficient supply contracts for fashion goods with forecast updating and two production modes[J]. Management Science, 2000, 46(11):1397-1411. [5] 李健,史浩. 需求预测更新条件下两阶段电子商务供应链契约协调[J]. 运筹与管理, 2016, 25(2):24-35. [6] 简惠云,王国顺,许民利. 具有两阶段生产模式和需求信息更新的供应链契约研究[J]. 中国管理科学, 2013, 21(1):80-89. [7] 胡觉亮,孔云鹏,韩曙光,等. 需求信息更新下服装供应链的最优订货决策研究[J]. 纺织学报, 2012, 33(11):136-140. [8] 尚文芳,祁明,张智勇. 基于需求信息更新和短缺量延期供给的易逝品供应链期权契约研究[J]. 管理学报, 2012,9(6):908-912. [9] 宋华明,杨慧,罗建强. 基于Bayes需求预测更新的供应链合作策略研究[J]. 管理工程学报, 2011,25(2):220-227. [10] PASTERNACK B A. Optimal pricing and returns policies for perishable commodities[J]. Marketing Science, 2008, 27(1): 131-132. [11] 邓欣.基于损失厌恶偏好的供应链回购契约[D].重庆:重庆交通大学, 2012:24-29. [12] PORTEUS E. Responsibility tokens in supply chain management[J]. Manufacturing & Service Operations Management, 2000, 2(2): 203-219. [13] PADMANABHAN V, PNG I P L. Manufacturer’s returns policy and retail competition[J]. Marketing Science, 1997, 16(1): 81-94. [14] LARIVIERE M, PORTEUS E. Selling to the newsvendor: an analysis of price-only contracts[J]. Manufacturing & Service Operations Management, 2001, 3(4):293-305. [15] CACHON G, RARD P, LARIVIERE M A. Supply chain coordination with revenue sharing contracts: strengths and limitations[J]. Management Science, 2005, 51(1):30-44. [16] TSAY A. The quantity-flexibility contract and supplier-customer incentives[J]. Management Science, 1999, 45(10): 1339-1358. [17] TAYLOR T A. Supply chain coordination under channel rebates with sales effort effect[J]. Management Science, 2002, 48(8): 992-1007. (责任编辑: 康 锋) Ordering Strategy for a Supply China with Limited Storage Capacity and Demand Updating WENXin,GUOYongjiang (School of Sciences, Beijing University of Posts and Telecommunications, Beijing 100876, China) In this paper, we studied the ordering strategy for a supply chain with limited storage capacity and demand updating in the setting of the sale of seasonal products. The supply chain consists of one supplier and one retailer. The retailer is assumed to have two opportunities to place order before and after receiving demand signals respectively, and the first order is limited by the storage capacity. We obtained the optimal ordering strategy with no storage capacity limit by setting parameter indexes according to the properties of derivative with backstepping method, and then got the optimal ordering strategy with limited storage capacity according to the properties of the concave function in different cases, to balance the supply chain. At last, we verified the correctness of the result via numerical example, and further explained the optimal ordering strategy. storage capacity limit; demand signal; supply chain; buy-back contract 10.3969/j.issn.1673-3851.2017.08.003 2017-02-26 网络出版日期:2017-06-21 国家自然科学基金项目(11471053) 温馨(1991-),女,山西晋中人,硕士研究生,主要从事供应链管理方面的研究。 F274 A 1673- 3851 (2017) 04- 0299- 07


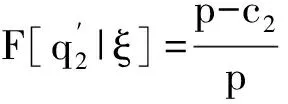
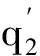



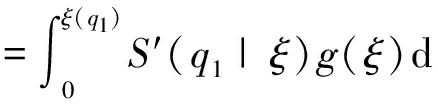
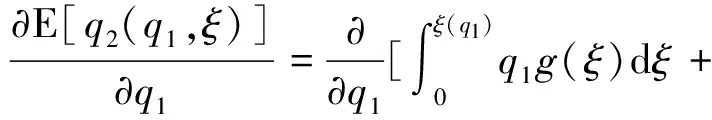


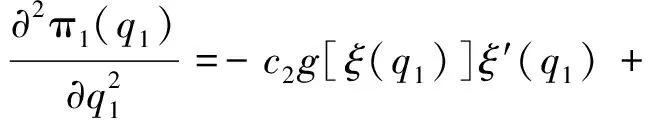

二、算例分析

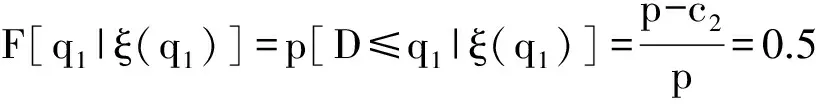
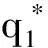
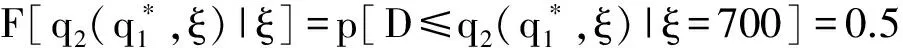
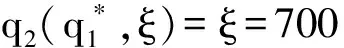
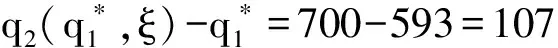

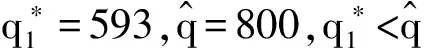

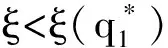


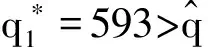
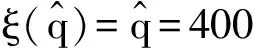

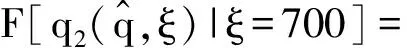




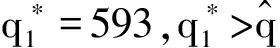
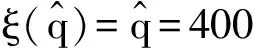

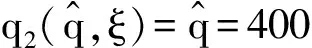

三、结 语

