考虑二维装箱约束的多车场带时间窗的车辆路径问题模型及算法研究

颜 瑞，朱晓宁，张 群，戚耀元，蔺俞铮

(1. 北京信息科技大学，北京 100192；2.北京科技大学，北京 100083)



考虑二维装箱约束的多车场带时间窗的车辆路径问题模型及算法研究

颜 瑞1，朱晓宁2，张 群2，戚耀元2，蔺俞铮1

(1. 北京信息科技大学，北京 100192；2.北京科技大学，北京 100083)

研究包含时间窗、多车场因素的二维装箱车辆路径问题，建立相应的数学模型，并提出求解该问题的一种新的混合算法，混合算法由量子粒子群算法和引导式局部搜索算法组成。其中，量子粒子群算法用于求解车辆路径问题，引导式局部搜索算法用于求解可行装箱方案。在引导式局部搜索算法中，提出一种基于最小浪费原则的启发式装箱规则，以灵活确定待装货物和装货空间之间的匹配关系，减少重复确定装箱方案所消耗的时间。设计了两组数值试验：第一组基于标准算例库，并将混合算法计算结果与已有文献中的结果进行对比；第二组基于随机生成的新算例，新算例给出多车场和时间窗数据，用于演示混合算法对新模型的计算过程和计算结果。两组数值试验的结果表明，混合算法在效率和性能方面均有较好的表现，计算结果和计算时间均优于已有文献，且混合算法能够较好的求解包含时间窗、多车场因素的二维装箱车辆路径问题模型。

车辆路径问题；二维装箱问题；量子粒子群算法；多车场；时间窗

1 引言

二维装箱约束的车辆路径问题(Two-Dimensional Loading Capacitated Vehicle Routing Problem，2L-CVRP)是带容量约束的车辆路径问题(Capacitated Vehicle Routing Problem，CVRP)和二维装箱问题(Two-Dimensional Bin Packing Problem，2BPP)的联合优化问题，近年来逐渐引起了相关领域学者的关注。现实的物流配送中有很多情况归属于2L-CVRP。比如，由于易碎、易损等原因，在物流配送过程中经常存在货物不可相互叠放的情况，那么货物能否装车就取决于货物底面能否拼装入车厢底面中。对于这类问题，“装箱”和“运输”这两方面是不可分割、相互制约的，只有综合考虑这两点才能既保证选择的配送路线成本最低，又保证货物可以全部合理地装入车厢。由于CVRP和2BPP均属于NP-hard问题[1-3]，且配送物品能否顺利装箱、装箱顺序等都会影响车辆配送任务的分配及配送路径的规划。因此2L-CVRP的启发式求解策略难以提炼，大规模问题的求解效率有待提高。2L-CVRP由Iori于2005年最早开始研究，目前为止大部分相关文献均注重研究更高效的求解算法，鲜有在模型方面进行改进的研究成果[2]。

很多学者提出了不同的算法对2L-CVRP问题进行求解，改善了Iori最初求解结果。Gendreau等[4]提出了禁忌搜索算法用于优化装箱问题的求解策略，算法中对于非可行解赋予一定的惩罚值，设计了一种不同线路中客户交换的邻域搜索策略，并运用分支定界法检测装箱可行性。Zachariadis等[3]在Gendreau等人的研究成果之上，结合禁忌搜索算法与引导性局部搜索策略，提出了引导性禁忌搜索算法，在一定程度上降低了产生低质量解的可能性，提高了算法的效率。Leung等[5]改进了引导性禁忌搜索算法，并融入模拟退火算法的思想，进一步提升了算法求解精度。Fllellerera等[6]以蚁群算法为主导，融入了同时考虑装箱和路径的启发式策略，并对2L-CVRP的四个变种问题分别进行了研究，在Iori提出的标准算例库上取得了较好的测试结果。Duhamel等[7]将贪婪随机自适应搜索算法与进化迭代局部搜索算法 (GRASP×ELS) 相结合，计算结果与之前文献中的结果相比有了较明显的改善，但其模型并未考虑货物的装卸顺序。2010年，Iori和Martello[8]对CVRP和BPP的研究进行了系统的总结，明确了一些基本概念和基本问题，包括2L-CVRP、3L-CVRP及带装箱约束的装卸一体旅行商问题(Traveling Salesman Problems with Pickup & Delivery and Loading Constraints， TSPPDL)等。文献[9,10]针对2L-CVRP的有向有序的变种问题，分别提出了两种分支定界法进行求解。Zachariadis等[11]近期又提出了一种改进的元启发式算法，该算法显示出了良好的性能并且改善了很多标准算例库中已有的最优结果。文献[12]应用分支切割法求解3L-CVRP问题，该算法使用了几种技术来修剪树枝和削减枚举树，在较短的计算时间内得出较佳的解决方案。最近，Wei等[1]提出了可变邻域搜索算法解决路径规划问题，并采用基于“skyline”启发式搜索策略的算法检验装箱约束，并通过标准算例库验证了该方法的有效性，但是其研究主要针对的是无向有序2L-CVRP问题。Zachariadis等[13]研究了同时考虑客户加载需求和装箱约束的二维配送车辆路径优化问题，这是2L-CVRP的一个变种问题。从管理的角度来看，服务的交付和选择可能会带来可观的成本节约，但在合理时间内完成广义负载限制的计算是比较困难的，虽然其在算法中增加了后进先出约束，并禁止路径重排，在提高计算速度的同时降低了最优解质量。

目前，国内关于CVRP和BPP联合问题的研究成果相对较少。马珊静和陈峰等人研究了一维装箱和车辆路径的联合问题，以最小化仓储成本、运输成本和车辆运营成本总和为目标，提出了三种不同策略的两阶段启发式算法进行求解[14]。宁爱兵和熊小华等人研究了物流配送中的三维装箱问题，考虑到三维装箱和车辆路径相结合的一些基本问题，并提出了一种求解三维装箱问题的算法，但是文献并没有把两个问题联合起来进行建模和求解[15]。王征和胡祥培等人针对易损、易碎物品的运输问题进行研究，建立了较为完整的2L-CVRP数学模型，并提出了求解该模型的一个Memetic算法，算法中设计了一种基于深度优先的装箱问题求解策略，文献采用Iori提出的标准算例进行计算，全面分析了Memetic算法的求解效率、求解性能和鲁棒性，试验取得了较为理想的结果[16]。颜瑞等[17]建立考虑三维装箱约束的车辆路径问题模型，提出求解该问题的引导式局部搜索算法，算法平均计算结果优于标准算例库中的已有结果。

在基本的2L-CVRP问题中，仅假设有一个中心车场，客户的需求被定义为若干个有重量的二维矩形物体，而车辆拥有相同的载重限制和装载空间限制。相比2L-CVRP问题，本文所研究的考虑二维装箱约束的多车场带时间窗车辆路径问题更具有普适性，现实中大量的物流车辆调度问题都可以归结为此类问题：车辆分布于不同物理地点上的车场，他们要将货物合理地装入车厢，并且用最低的成本在要求的时间范围内将指定数量的物品送达顾客，最后返回车场。将时间窗加入车辆配送路径问题方面已有一些研究成果。Errico等[18]研究考虑硬时间窗和随机服务时间的车辆路径优化问题，并改进了标签算法，通过适当选择标签组件，制定上下边界的部分路径从而降低成本，取得了较好的解决方案。Keskin和Catay[19]研究了带时间窗的电动汽车车辆路径问题。但是上述文献并未综合考虑装箱约束和多车场问题。文献[20]研究了多车场带时间窗CVRP问题，建立了该问题的整数规划数学模型，提出了一种改进变邻域搜索算法，但未考虑装箱约束。“二维装箱”、“多车场”与“时间窗”分别在问题的空间、时间、流程等方面施加了多重约束，使原本具有NP复杂性的问题更加难以求解。

在第2章中，给出考虑二维装箱约束的多车场带时间窗车辆路径问题(Two-Dimensional Loading Capacitated Vehicle Routing Problem with Multi-Depots and Time Window，2L-CVRP-MDTW)的基本概念和假设，并在此基础之上建立完整的数学模型。在第3章中，提出量子粒子群算法和引导式局部搜索算法结合的混合算法，详细描述算法的策略和实施步骤。在第4章中，进行了两组数值试验，分析混合算法的性能和效率，演示2L-CVRP-MDTW模型的求解过程进行。

2 模型建立

2.1 问题描述

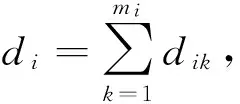
2.2 模型假设

本文对2L-CVRP-MDTW模型做出如下假设：

(1)假设每个车场处均有一个储货量充足的仓库，且每个车场的车辆仅从同一位置的仓库装货；

(2)确定若干条回路作为车辆行驶路线，每条线路的总距离不能超过车辆最大行驶距离，所有回路均从车场出发并返回车场，每个顾客仅能在一条回路上，每条回路上的顾客仅由一辆车服务；

(3)每条线路上顾客的货物总重量不能超过车辆载重、货物总占地面积不能超过车厢面积；

(4)每条线路上顾客需求的货物必须全部装入车厢，且满足全部给定的装箱约束：货物不能重叠放置，货物边缘必须与相应车厢边缘平行，货物不可旋转，在服务当前顾客时不用挪动其他顾客的货物(后进先出原则)；

(5)货物从车厢尾部的车门进出，假设装货工具可以把货物摆放到车厢内任意位置；

(6)车辆必须在顾客的时间窗内为其提供服务，不考虑车辆进出车场的时间窗；

(7)以所有车辆的行驶路程之和最小为目标。

图1给出了一个2L-CVRP-MDTW模型示意图，模型包括2个车场、9个顾客和21个货物。

图1 2L-CVRP-MDTW模型示意图

模型中的线路有两条：车场Ⅰ- 1 - 2 - 3 - 4 - 5 -车场Ⅰ；车场Ⅱ- 6 - 7 - 8 - 9 -车场Ⅱ。车辆装载方案如图2所示。

图2 2L-CVRP-MDTW模型装箱方案示意图

2.3 数学模型

在建立数学模型之前，需要先建立一个笛卡尔坐标系。坐标系的坐标轴分别对应车厢的长和宽，坐标系的原点对应车厢左上角。货物左上角的位置用坐标(x,y)表示，则有：

从而可以将车厢分割成若干个网格，如图3所示。

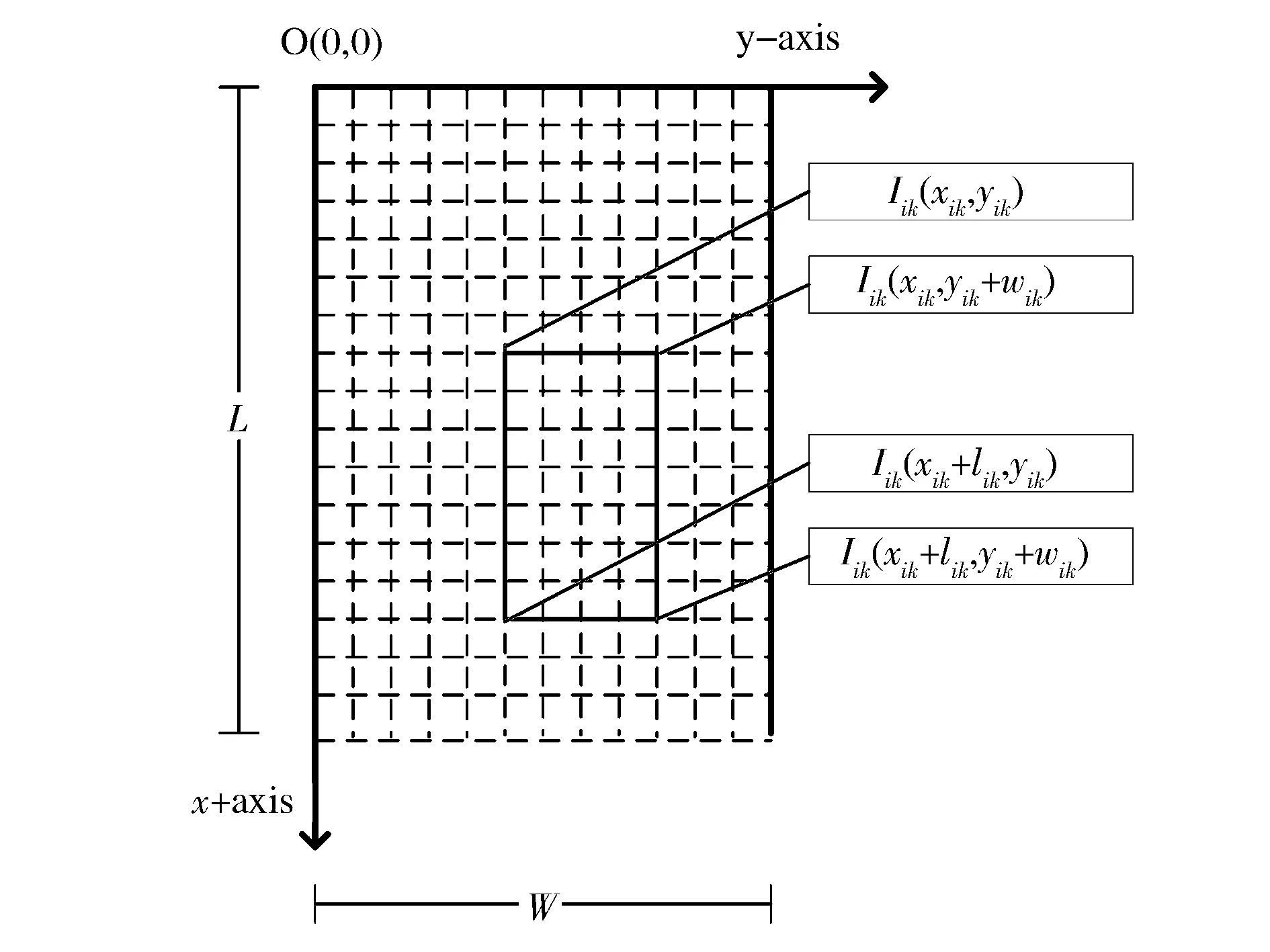
图3 车厢网格图和笛卡尔坐标系

表1给出数学模型中所用到的符号。

模型的决策变量有：

其中，i,i′=1,…,n+T,p=1,2,…,Pt,t=1,…,T。

表1 模型符号及符号解释

基于上述定义，建立2L-CVRP-MDTW的数学模型如下：

(1)

(2)

(3)

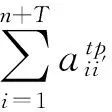
(4)

(5)

(6)

(7)

0≤xik≤W-wik,k=1,2,…,mi,i=1,2,…,n,

(8)

0≤yik≤L-lik,k=1,2,…,mi,i=1,2,…,n,

(9)

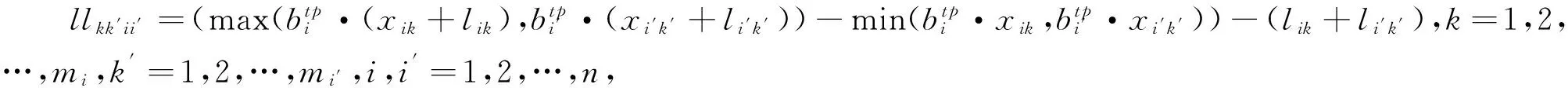
(10)

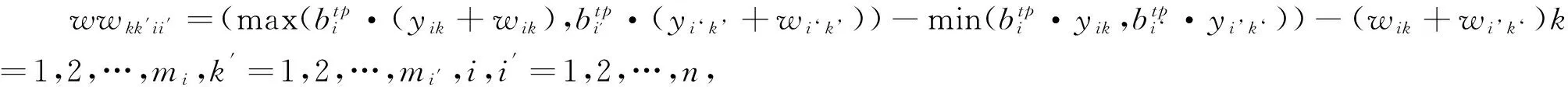
(11)

max(llkk′ii′,wwkk′ii′)≥0,k=1,2,…,mi,k′=1,2,…,mi′,i,i′=1,2,…,n,若i=i′,则k≠k′,

(12)

(13)

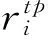
(14)

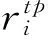
(15)

式(1)为目标函数，表示最小化车辆行驶总路程；式(2)表示每个顾客仅能在一条回路上；式(3)～(5)表示车辆进入某个节点则必须从该节点离开；式(6)表示每辆车装载的货物不能超过车辆载重；式(7)表示每辆车所装载货物的总面积不超过车辆底面积；式(8)和式(9)表示货物不能超过车厢边界；式(10)、式(11)和式(12)表示货物不能重叠放置；式(13)表示满足后进先出原则；式(14)和式(15)表示在时间窗内服务顾客。

3 算法设计

目前，已有文献中的优化算法均不能够直接用于求解2L-CVRP-MDTW模型。在分别研究考虑二维装箱约束、多车场和时间窗等因素的车辆路径问题求解算法的基础之上，本文提出一种结合量子粒子群算法和引导式局部搜索算法的混合算法求解2L-CVRP-MDTW模型。本节将详细描述混合算法的基本原理、各部分策略和实施步骤。本文模型和算法中的符号或有重复，但符号的意义完全不同，符号的意义仅在对应的模型或算法中进行解释。

3.1 量子粒子群算法

美国学者Kennedy和Eberhart受到鸟群觅食行为的启发提出了粒子群算法(Particle Swarm Optimization，PSO)，PSO具有精度高、收敛快和容易实现等优点[21]。算法提出后不久就被用于求解VRP问题，目前已有许多运用PSO求解VRP及其变种问题的文献[22-23]。在标准PSO中，种群由一定数量的粒子组成，每个粒子的位置均代表一个可行解。在多维搜索空间中，每个粒子均按照某个特定速度向更好的解移动。

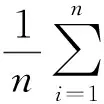
(16)

pid=φ*Pid+(1-φ)*Pgd,φ=rand(0,1),

(17)

(18)

其中，M表示粒子群中粒子的数目；d为粒子维度；mbest表示在所有粒子中每个粒子搜索到的最优位置的平均值，本文采用最接近平均适应值的粒子所在的位置；Pi=(Pi1,Pi2,…,Pid)表示第i个粒子的最优位置；Pgd表示所有粒子中最佳粒子所在的位置；pid表示在Pid和Pgd之间的一个随机点，在第i个粒子d维空间的一个位置；φ和u是在[0,1]之间均匀分布的随机数；α是QPSO算法的参数，称为收缩-扩张系数，一般采用线性递减的方式取值，其公式为：

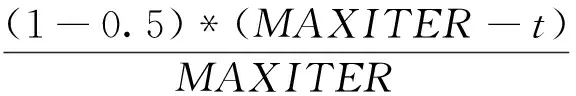
(19)

量子粒子群优化算法过程如下：

步骤1.初始化种群，粒子的初始位置通过随机方式产生；

步骤2.对于每一个粒子，计算其适应值，保存每个粒子历史最优值Pid,以及所有粒子的最优值Pgd；

步骤3.根据公式(16)计算mbest,即最接近所有粒子的平均适应值的粒子所在位置；

步骤4.对于粒子的每一个维，通过公式(17)得到一个随机点；

步骤5.通过公式(18)获得一个新的位置Xid；

步骤6.执行局部扰动操作；

步骤7.重复步骤2-步骤6，直至达到最大迭代次数。

为了便于实现，将时间窗约束作为惩罚项一并计入适应值中，惩罚参数设定为足够大的正整数。

3.1.1 改进的编码方法

考虑到多车场和时间窗的因素，现有文献中的编码方式均不适用。因此，本文构造了一种新的编码方式，即用4×n的矩阵形式进行编码。如图4所示，第一行Client为客户编号，第二行Xd为车场编号，第三行Xv为车辆编号，第四行Xt为车辆行驶顺序。4×n矩阵式编码方式增加了粒子的维数，而维数的增加并未显著增加PSO算法的计算复杂性，这点已经被相关研究证实[18]。

图4 编码方式示意图

在图4的例子中，第一列表示：从第一个配送中心出发的第一辆车辆服务顾客1，且顾客1位于该车辆的第一个拜访顺序上。由此，可写出编码示例的所有线路，如图5所示。

图5 编码示例对应的全部路径

以上所给出的粒子编码与解码方式能够保证使每个客户都得到服务，并限制每个客户仅能由一辆车完成，降低了寻优过程中产生非可行解的几率。

3.1.2 局部扰动

为了提高QPSO的寻优效率，本文采用2-opt和线路内部搜索两个方法进行局部扰动，这两种方法类似于遗传算法中的变异算子。2-opt作用于两条线路上，具体操作方法是：随机选择两条线路，并随机选择两个位置，将两条线路上的对应节点进行互换。线路内部搜索作用于单条线路上，具体操作方法是：随机选择一条线路，并随机选择两个位置，将两个位置对应的节点进行互换。

3.2 引导式局部搜索算法

由3.1中的量子粒子群算法可求解得最优线路，并可以确定每条线路上有哪些客户，以及每条线路由哪辆车服务。本节讨论如何将货物装入各自车厢内，且满足所有装载约束。一般的装箱问题以装载货物数最大为目标，而在2L-CVRP-MDTW的装箱问题中每辆车装载的货物数量和形状是固定的，因此其解空间仅是一般装箱问题解空间的一个子集。针对这样的特点，我们将设计一系列引导策略搜索问题的局部最优解。2L-CVRP-MDTW的装箱过程包括确定待装货物顺序和确定可行装货位置两个子问题，下面分别给出这两个子问题的求解策略。

3.2.1 确定待装货物顺序

对于一条给定的配送线路而言，该线路上的所有客户及客户顺序也是固定的。如第2章所描述的，在服务当前客户时不用挪动其他客户的货物，因此同一条线路上的货物应首先按照服务客户的顺序逆向安排，遵循后进先出原则。因此，不同客户的货物装箱顺序是固定的，但是同一个客户的货物装箱顺序不唯一。本文提出两种装箱规则以确定同一个客户的货物装箱顺序：O1规则按照装箱底面积l·w降序排列；O2规则按照货物长度l降序排列。首先按O1原则排序，如果两个货物底面积相同，则按O2原则排序。对于第2章中的例子来讲，两条线路上的货物顺序可排列为：

Rout1:I52-I51-I41-I33-I32-I31-I21-I23-I22-I12-I13-I11,

Rout2:I62-I63-I61-I71-I72-I81-I82-I92-I91。

3.2.2 确定可行装货位置

车厢的可行装货位置指的是装货列表中的下一个货物能够放置的位置。每装入一个货物之后，可行装货位置会发生变化。通常可行装货位置并不唯一，那么我们需要对可行装货位置按某种规则进行排序。已发表的文献中给出了几种确定可行装货位置的方法，但是这些方法通常仅按照固定的规则逐一尝试，容易造成后面的货物不能全部装入车厢，需要进行重复计算，降低了求解效率。因此，本文给出一种新的基于匹配规则的启发式装箱方法，充分考虑到货物与位置之间的匹配关系，将待装货物放在最合适的位置上，尽可能充分节省空间，以提高一次装箱成功率。

对于列表中的第一个货物，我们通常将它放置在车厢的左下角(车门在正上方)，即图6中的点O(0, 0)处。需要注意的是，当我们描述把货物放在某个位置时，则表示该货物左下角的坐标落在该位置点上。此外，由于所有货物占据的网格数均为整数，因此某个点被货物占据的意思就是，包含该点且处于其右上方的网格被该货物占据。例如，点O处放置一个货物，则(0, 0)、(0, 1)、(1, 0)和(1, 1)所组成的网格被该货物占据。当装入一些货物之后可能会出现一系列新的装货位置。如图6所示，在装入A后，可行装货位置列表更新为：

position_list={a(0,W,L-lA),b(1,W-1,L-lA),c(2,W-2,L)}。

图6 可行装货位置示意图

在所有的可行装货位置中，我们下一步要做的事情就是根据当前货物的形状，选择一个最理想的位置作为当前装货位置。在确定最理想装货位置的时候，我们应当遵循一个最基本的原则，就是充分节省空间。基于这样的原则，我们给出如下规则对可行装货点进行排序，得到每个可行装货点的优先级。如图7所示，图中白色区域为已放置货物，灰色区域为剩余空间，R为待装的下一个货物。当剩余空间大小相同，而待装货物大小不同时，可以产生如下准则：

a.货物与可行区长宽相等，适应值为1，如图7(a)。

b.货物宽度与可行区宽度相等，货物长度小于可行区长度，适应值为2，如图7(b)。

c.货物长度与可行区长度相等，货物宽度小于可行区宽度，适应值为3，如图7(c)。

d.货物宽度小于可行区宽度，货物长度小于可行区长度，适应值为4，如图7(d)。

e.货物宽度大于可行区宽度或货物长度大于可行区长度，适应值为无穷大，即货物无法放置于该位置。

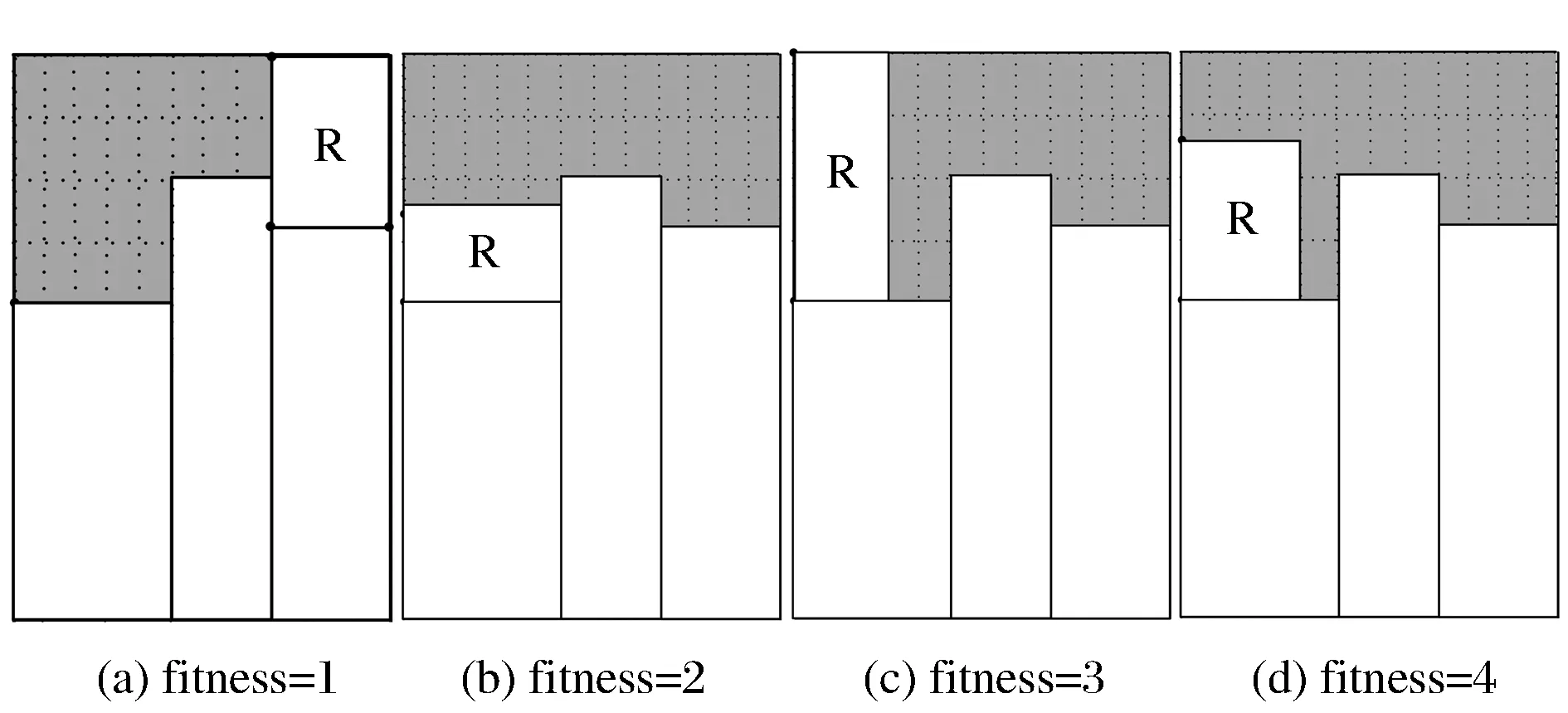
图7 可行装货位置的适应值

3.3 混合算法

本文把量子粒子群算法和引导式局部搜索算法结合起来，构造求解2L-CVRP-MDTW的引导式局部搜索量子粒子群算法(Guided Local Search - Quantum-behaved Particle Swarm Optimization Algorithm，GLS-QPSO)。GLS-QPSO算法的基本思路为：通过量子粒子群算法得到VRP的近似最优解集，近似最优解集中保存适应度靠前的若干粒子；把最优解集中的粒子按适应度从大到小排列，选择第一个粒子作为当前车辆路线方案，然后调用引导式局部搜索算法；如果找到可行装箱方案，则返回最优解，否则，依次选择最优解集中的下一个解作为车辆路线方案；如果最优解集中所有车辆路线方案均找不到可行解，则返回量子粒子群算法重新求解VRP；重复算法直至找到可行解，或达到最大迭代次数。若达到最大迭代次数仍未找到最优解，则应考虑减少顾客或货物数量，或者增加车辆总数，然后重新执行GLS-QPSO算法。

GLS-QPSO算法的具体步骤如下：

步骤1. GLS-QPSO算法初始化：设定最大循环次数T,令t=0；

步骤2.执行QPSO算法流程，详见3.1；

步骤3.生成近似最优解集：QPSO算法结束之后，按适应度从大到小排列当前粒子，保留靠前的BestSize个粒子形成近似最优解集；

步骤4.引导式局部搜索算法参数初始化：令i=1,j=1,k=1；

步骤5. 产生车辆路线方案：选择近似最优解集中的第i个解，作为当前车辆路线方案；

步骤6.初始装货序列：按照车辆服务顾客顺序的相反顺序排列货物，相同顾客的货物按照非易碎品在前、易碎品在后的顺序排列；

步骤7.最终装货序列：按照Oj规则调整装货顺序，确定最终装货序列；

步骤8.可行装货位置：按照第k个启发式方法扫描所有可能装货位置，按装货序列给每个货物都找到可行装货位置；

步骤9.可行装货位置循环：若所有货物均找到可行装货位置，算法终止，输出当前最优解；若有一个或多个货物没找到可行装货位置，且k<6,令k=k+1,返回步骤8；若k≥6,转步骤10；

步骤10.装货序列循环：若j<3,令j=j+1,返回步骤7；若j≥3,转步骤11；

步骤11.近似最优解集循环：若i

步骤12.总循环：若t

4 数值试验

本文设计了两组数值试验。第一组数值试验基于已有标准算例库，用于检验GLS-QPSO算法的性能和效率。第二组数值试验基于随机生成的算例，用于演示GLS-QPSO算法对2L-CVRP-MDTW模型的求解过程和计算效果。

4.1 基于标准算例库的数值试验

Gendreau等[4]中给出了180个2L-CVRP算例，这些算例均是在Toth和Vigo[25]所给出的36个CVRP算例的基础上转化而来。随后，有一些设计不同算法求解2L-CVRP的问题的文献陆续发表出来，均采用Gendreau等[4]的算例进行数值试验，其中Leung等[5]的计算结果较好。

从180个算例中随机抽取20个进行数值试验，在这20个算例中车厢规格相同(长为40、宽为20)。将本文计算结果与Duhamel等[4]和Duhamel等[7]的优化结果进行对比，如表2所示，“Best”表示最优路径，“Time”表示计算时间，“Gap”表示最优解和时间的降低幅度。

表2 与已有文献计算结果对比

注：“Gap”值为正表示本文结果优于已有结果，为负表示本文结果劣于已有结果。

从表2中的对比结果可以发现，本文的计算结果在最短路径和计算时间上均有较好表现。其中，最短路径比Gendreau等[4]平均减少11.23%，比Duhamel等[7]平均减少1.07%，本文在计算结果上与Duhamel等[7]相当。计算时间比Gendreau等[4]平均减少619.10秒，比Duhamel等[7]平均减少96.36秒，本文在计算时间上具有明显优势。Gendreau等[4]采用禁忌搜索算法进行求解，优点在于逻辑清晰、容易实现，缺点在于处理大规模问题时效果较差。

4.2 基于随机数据的数值试验

由于2L-CVRP-MDTW模型没有现成算例，因此本文将给出一个新算例，并用新算例演示模型求解过程和结果。本文在标准算例0201的基础上，通过新增一个新车场，并为每个顾客指定时间窗，从而形成一个多车场、带时间窗的二维装箱车辆路径问题算例。原始数据参考标准算例库，新车场坐标为(35，45)，顾客时间窗见表3。

假设所有车辆8:00开始出发，17:00返回各自车场。原始算例中的节点坐标没有单位，本文假设所有节点坐标的单位均为千米，且假设车辆行驶速度为50千米/小时。计算出的最优路径如图8所示。

表3 顾客时间窗列表

图8 新算例车辆最优路线示意图

在图9中有两条路线存在交叉现象，可以看出线路交叉是为了满足时间窗约束。

5 结语

本文研究了2L-CVRP的一个变种问题，在传统2L-CVRP模型中综合考虑多车场和时间窗因素，给出变种问题的目标和约束，并建立2L-CVRP-MDTW模型。为了更好的求解2L-CVRP-MDTW模型，本文提出了一种基于量子粒子群算法和引导式局部搜索算法相结合的混合算法。量子粒子群算法在传统粒子群算法的基础上，给每个粒子增加量子行为，提高粒子的搜索能力，并从整体上提高粒子群算法的性能。引导式局部搜索给出一种新的启发式装箱规则，即根据最小浪费原则灵活确定待装货物与装货空间之间的匹配关系。

为了检验GLS-QPSO算法的效率和性能，本文在标准算例库中随机抽取了20个算例进行数值试验，并将试验结果与已有文献中的结果进行对比。对比结果表明，GLS-QPSO算法在计算结果和计算时间上均有较为优秀的表现，明显优于已有文献中的算法。此外，为了检验本文所提出的2L-CVRP-MDTW模型的可解性，在原有算例的基础上生成一个新算例进行数值试验。新算例给出第二个车场的坐标，并给出每个顾客的服务时间窗。GLS-QPSO成功计算出新算例的最优路径，所有线路均满足既定约束，并且服务顾客的开始时间均处于规定的时间窗内。从这两组数值试验可以得出这样的结论：一是，GLS-QPSO算法具有较好的效率和性能；二是，GLS-QPSO算法能够很好的处理2L-CVRP-MDTW模型，并在有效时间内给出问题的最优解。

[1] Wei Lijun, Zhang Zhenzhen, Zhang Defu, et al. A variable neighborhood search for the capacitated vehicle routing problem with two-dimensional loading constraints [J]. European Journal of Operational Research, 2015, 243(3):798-814.

[2] Iori M. Meta-heuristic algorithm for combinatorial optimization problems [J]. 4OR, 2005, 3(2): 163-166.

[3] Zachariadis E E, Tarantilis C D, Kiranoudis C T. A guided Tabu search for the vehicle routing problem with two-dimensional loading constraints [J]. European Journal of Operational Research, 2009, 195( 3): 729-743.

[4] Gendreau M, Iori M, Laporte G, et al. A Tabu search heuristic for the vehicle routing problem with two-dimensional loading constraints [J]. Networks,2008,51(2):469-477.

[5] Leung SCH, Zheng Jiemin, Zhang Defu, et al. Simulated annealing for the vehicle routing problem with two-dimensional loading constraints [J]. Flexible Services & Manufacturing Journal, 2010, 22(1): 61-82.

[6] Fuellerer G, Doerner K F, Hartl R F, et al. Ant colony optimization for the two-dimensional loading vehicle routing problem [J]. Computers & Operations Research, 2007, 36(3): 655-673.

[7] Duhamel C, Lacomme P, Quilliot A, et al. A multi-start evolutionary local search for the two-dimensional loading capacitated vehicle routing problem [J]. Computers & Operations Research, 2011, 38(3): 617-640.

[8] Iori M, Martello S. Routing problems with loading constraints [J]. Top, 2010, 18(1): 4-27.

[9] Iori M, Juan-José, Salazar-Gonzá, et al. An exact approach for the vehicle routing problem with two-dimensional loading constraints [J]. Transportation Science, 2007, 41(2): 253-264.

[10] Bruno LP, Pedro H, Flavio K, et al. A branch-and-cut approach for the vehicle routing problem with two-dimensional loading constraints [J]. Transportation Science, 2007, 41(2):253-264.

[11] Zachariadis EE, Tarantilis C D, Kiranoudis CT. Integrated distribution and loading planning via a compact metaheuristic algorithm [J]. European Journal of Operational Research, 2013, 228(1): 56-71.

[12] Hokama P, Miyazawa KF, Xavier C E. A branch-and-cut approach for the vehicle routing problem with loading constraints [J]. Expert Systems With Applications, 2016,47: 1-13.

[13] Zachariadis E E, Tarantilis D C, Kiranoudis T C. The vehicle routing problem with simultaneous pick-ups and deliveries and two-dimensional loading constraints [J]. European Journal of Operational Research, 2016,251(2): 369-386.

[14] 马珊静，陈峰，宋德朝,等. 越库配送物流系统车辆调度算法的研究[J]. 现代制造工程， 2009,(1)：12-15.

[15] 宁爱兵，熊小华，马良. 城市物流配送中的三维装箱算法[J]. 计算机工程与应用， 2009， 45(9)：207-208.

[16] 王征，胡祥培，王旭坪. 带二维装箱约束的物流配送车辆路径问题[J]. 系统工程理论与实践，2011，31(12)：2328-2341.

[17] 颜瑞，张群，胡睿. 考虑三维装箱约束的车辆路径问题研究[J]. 中国管理科学， 2015， 23(1)：128-132.

[18] Errico F, Desaulniers G, Gendreau M, et al. A priori optimization with recourse for the vehicle routing problem with hard time windows and stochastic service times [J]. European Journal of Operational Research, 2016,249(1): 55-66.

[19] Keskin M, Catay B. Partical recharge strategies for the electric vehicle routing problem with time windows [J]. Transportation Research Part C:Emerqing Technologies, 2016,65:111-127.

[20] 王征，张俊，王旭坪. 多车场带时间窗车辆路径问题的变领域搜索算法[J]. 中国管理科学， 2011，19(2)： 99-103.

[21] Kennedy J, Eberhart R C. Swarm intelligence [M]. San Francisco:Morgan Kaufman Publishers,2001.

[22] Ai T, Kachitvichyanukul V. A particle swarm optimization for the vehicle routing problem with simultaneous pickup and delivery [J]. Computers & Operations Research, 2009, 36(5): 1693-1702.

[23] Wu Z. Optimization of distribution route selection based on particle swarm algorithm [J]. International Journal of Simulation Modelling, 2014, 13 (2): 230-242.

[24] Sun Jun, Xu Wenbo, Feng Bin. A global search strategy of quantum-behaved particle swarm optimization [C]//Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems, Singapore,December 1-3,2004.

[25] Toth P, Vigo D. The vehicle routing problem, chapter branch-and-bound algorithms for the capacitated VRP [J]. Siam Monographs on Discrete Mathematics & Applications, 2002, 94(2-3): 127-153.

Research ofthe Model and Algorithm for Two-dimensional Multi-depots Capacitated Vehicle Routing Problem with Time Window Constrain

YAN Rui1, ZHU Xiao-ning2, ZHANG Qun2, QI Yao-yuan2, LIN Yu-zheng1

(1.Beijing Information Science and Technology University,Beining 100192,China;2.University of Science and Technology Beijing,Beijing 100083,China)

Both vehicle routing problem (VRP) and bin packing problem (BPP) are important, typical combinatorial optimization problems, and are frequently and independently studied in the past few decades. In recent years, some attention has been devoted to their combined optimization, called 2L-CVRP (two-dimensional capacitated vehicle routing problem), which is a combination of two important NP-hard optimization problems in distribution logistics. In the 2L-CVRP, clients demand are defined as sets of rectangular weighted items, while vehicles have a weight capacity and a rectangular two-dimensional loading surface. The objective of the 2L-CVPR is to serve all the customers and load the corresponding items into the vehicles, through a road network, with minimum total cost.

Problem description：In this paper, a multi-depots capacitated vehicle routing problem with time window where client demand is composed of two-dimensional weighted items is addressed (2L-CVRP-MDTM).The model and an improved hybrid algorithm to solve the problem are proposed. The hybrid algorithm GLS-QPSO is composed by the Quantum-behaved Particle Swarm Optimization algorithm which is applied to solve the vehicle routing problem and Guided Local Search algorithm which is used to identify the feasible packing solutions.

Method：New loading heuristic rules are proposed in Guided Local Search algorithm based on the principle of minimize the waste to get better results of the matching relationship between the items and the corresponding packing positions in shorter time. Through the algorithm we can get the tours, and identify the clients covered by the vehicles, as well as vehicles in the routes. All the items demanded by the clients need to be loaded in the vehicles with the related constrains. In fact, there are two aspects that packing algorithm needs to consider. One is to determine the next loading item, and another is to determine the feasible loading position.

Computational experiments: Twenty of these 2L-CVRP standard instances are selected randomly, and loading surface (L,W) is fixed as (40,20) for all instances. The 20 selected instances are changed to two depots instances to testify the proposed algorithm in this paper by adding a new depot. We calculate the center of the clients, and then select a point between the first depot and the center randomly as the second depot.

Results：We compare the improved hybrid algorithm with the known best solutions, and the other is based on the new instances which include multi-depots with time window constrain. We calculate the center of the clients, and then select a point between the first depot and the center randomly as the second depot. The results of the numerical experiments show that the proposed hybrid algorithm has better performances in terms of both the calculation results and computing time comparing with the selected recent literature. The computational results show that the proposed algorithm is effective in finding high quality solutions and the practical recharging option may significantly improve the 2L-CVRP-MDTM which a new variant of the 2L-CVRP considering vehicles start from several different depots with time window constrains.

vehicle routing problem; two-dimensional packing problem; Quantum-behaved Particle Swarm Optimization algorithm; multi-depots; time window

2015-11-22；

2016-03-01

国家自然科学基金青年项目(71602008)；北京市社会科学基金研究基地项目(16JDGLC032)；北京交通大学人才基金(B15RC00150)

颜瑞(1986-)，男(汉族)，江苏连云港人，北京信息科技大学经济管理学院，讲师，博士，研究方向：物流优化、智能算法，E-mail:yr1900@163.com.

1003-207(2017)07-0067-11

10.16381/j.cnki.issn1003-207x.2017.07.008

O224

A