“矢量图”在轮船过河问题中的运用

肖正忠

（福建省大田第一中学）

摘 要：运动的合成与分解是高中物理的难点之一，也是近年高考出现频率最高的热点之一。通过一道典型的例题，浅析“矢量图”在轮船过河问题中的运用，以期抛砖引玉，共同探究轮船过河问题的解题方法与思路。

关键词：矢量图；运动的合成与分解；合运动；分运动

高中物理运动的合成与分解是个难点，也是高考的高频考点之一。轮船过河问题是运动的合成与分解最常见的题型之一，要解决该类问题，必须依据运动的独立性原理，明确合速度与分速度之间的矢量关系。轮船在流动的水中过河时，分析判断物体的合运动与分运动是解题的关键所在，实际运动即为合运动。两个分运动，分别是船相對水的运动与船随水流的运动。从理论上讲，对运动物体进行运动的分解是任意的，但实际上解决问题是按运动的实际效果进行分解的。

一、处理方法

在物理学中应用矢量图形进行解题，具有直观易懂、简洁明了的功效。在物理学中，按运算法则将物理量分为两大类：标量和矢量。

标量：只有大小，没有方向，只要物理单位相同就可以用简单的代数运算进行求解。例如：质量、长度、时间、温度等物理量都属于标量。

矢量：既有大小，又有方向，在物理单位相同的情况下，不能进行简单的用代数运算，而是要符合平行四边形法则。例如：速度、加速度、位移、力等物理量都属于矢量。

轮船在有一定流速的水中过河时，实际上参与了两个方向的分运动，即随水流的运动v水（水冲船的运动），和船相对水的运动v船（即在静水中的船的运动），船的实际运动v是合运动（看见的运动就是合运动）。三个矢量v水、v船与v必须满足平行四边形定则的“矢量图”，即矢量v水、v船为平行四边形的两条边，矢量v为平行四边形的对角线。

二、应用举例

物体运动的合成与分解理论，在生产生活中的应用有许多，其中轮船渡河问题是典型的应用之一，应用“矢量图”进行解题，图象清晰，求解结果一目了然。

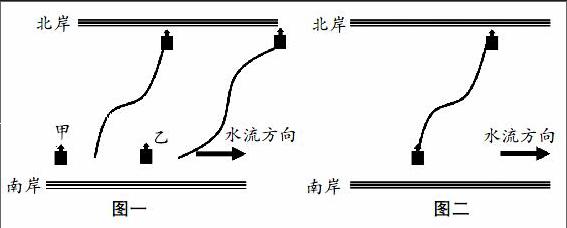
例：（多选）如下图所示，船横渡南北两岸平行的河流，船身方向垂直于河岸，则以下说法正确的是（ ）

A.如图一，若水流速度不变，则根据运动轨迹可判断甲船先加速后减速，乙船先减速后加速。

B.如图一，若水流速度不变，则根据运动轨迹可判断乙船先加速后减速，甲船先减速后加速。

C.如图二，若船本身提供的速度（即静水速度）大小不变，则根据运动轨迹可判断越接近河岸水流速度越大

D.如图二，若船本身提供的速度（即静水速度）大小不变，则根据运动轨迹可判断越接近河岸水流速度越小

解析：物体作曲线运动时，速度的方向沿曲线的切线方向，实际运动为合运动。

当水流速度v水大小不变时：由运动的合成与分解知识，以水流的运动v水（水冲船的运动）和船相对水的运动v船（即在静水中的船的运动）为临边作平行四边形，对角线v是轮船的实际运动即合运动。“矢量图”为下图三，从图中可直观得出正确的答案为B。

当船本身提供的速度v船大小不变时：由运动的合成与分解知识，以水流的运动v水（水冲船的运动）和船相对水的运动v船（即在静水中的船的运动）为临边作平行四边形，对角线v是轮船的实际运动即合运动。“矢量图”为图四，从图中可直观得出正确的答案为D。

所以本题正确答案为：B、D。

从以上解析可以看出，在解答轮船过河问题中，应用“矢量图”进行求解，能使复杂的物理问题变得容易，使抽象的物理问题变得直观。所以，在平时教学中引导学生应用“矢量图”进行求解物理问题，往往具有事半功倍的效果。

参考文献：

[1]蒋军.运动的合成与分解问题的典型解法与技巧[J].中学物理，2015（11）.

[2]杨海宝.“矢量的运算”在轮船过河问题中的运用[J].中学物理，2008（1）.

注：此文系2016—2018年度大田县基础教育教学研究重点

研究课题《高中生应用数学解决物理问题能力薄弱成因调查》（立项号：DTKTZX-2016042）阶段性成果。

编辑 温雪莲