一种基于时间序列算法的资金流入流出预测模型

曹 璨，黄 海，徐 可

(中国科学技术大学 信息科学技术学院，安徽 合肥 230027)



一种基于时间序列算法的资金流入流出预测模型

曹 璨，黄 海，徐 可

(中国科学技术大学 信息科学技术学院，安徽 合肥 230027)

资金的流入流出预测对于降低网络金融平台的流动性风险、提高资金利用率具有重要意义。根据资金流入流出历史数据，对蚂蚁金服公司余额宝资金未来30天流入流出的预测问题进行研究。由于历史数据不稳定且多噪声，首先采用序列转换方法对不平稳序列进行差分处理提高其数据稳定性，其次对该序列进行模型识别和参数估计，利用时间序列模型初步预测，并对残差序列进行模型检验，最后利用通过检验的模型预测结果。实验结果表明，此模型可以有效地对余额宝用户的资金流入流出金额进行预测。

资金流入流出预测；序列转换；参数估计；时间序列模型

0 引言

金融公司往往拥有千万乃至上亿的服务会员，公司的金融业务场景每天必然会涉及大量的资金流入流出，导致资金管理压力会非常大。因此，在保证资金流动性风险最小，同时满足日常业务运转的情况下，精准地预测资金的流入流出显得尤为重要。然而，金融数据的变动往往受社会、经济等多方面因素的影响，数据变化趋势不稳定，导致资金的流入流出预测较为困难。

国内外学者对资金流入流出的研究较少，且主要侧重于股票行情预测、证券价格预测等问题。 Soofi利用非线性拟合方法对含噪声的金融数据进行了预测[1]。FINANCE A基于多元非线性动力学理论对上海股票市场进行了短期预测[2]。Dai Wensheng等人采用非线性独立分量分析与神经网络相结合的方法，对亚洲股市指数进行了预测[3]。DAIGO K利用多时间序列的方法对股票价格趋势进行了研究[4]。与此同时，相关学者提出了电网短期负荷时间序列的混沌性预测模型[5]。

本文以蚂蚁金服公司余额宝资金预测为例，研究金融公司未来每天的资金流入流出预测问题，目标是对余额宝每天的资金流入流出总值进行预测。

本文针对资金流入流出数据的稳定性较差、多噪声的特点，首先结合业务背景进行数据预处理，采用序列转换方法对不平稳序列进行差分处理使其变得平稳，其次再进行模型识别和参数估计，利用合适的时间序列模型初步预测，并对残差序列进行模型检验，最后利用通过检验的模型训练学习，预测出目标月份未来每天的申购和赎回值。

1 背景描述

本文以余额宝流入流出资金为例，对金融公司资金的流入流出预测问题进行研究，其中货币基金的流入流出为申购行为和赎回行为的流动资金。

用户的申购赎回数据包括申购、赎回信息和所有的子类目信息。数据主要包括用户操作时间和操作记录，其中操作记录包括申购(purchase)和赎回(redeem)两个部分。

金融数据包括今日余额(tBalance)、昨日余额(yBalance)、今日总购买量(total_purchase_amt)、今日直接购买量(direct_purchase_amt)、今日支付宝余额购买量(purchase_bal_amt)、今日银行卡购买量(purchase_bank_amt)、今日总赎回量(total_redeem_amt)、今日消费总量(consume_amt)、今日转出总量(transfer_amt)、今日转出到支付宝余额总量(tftobal_amt)、今日转出到银行卡总量(tftocard_amt)、今日收益(share_amt)和今日类目1-4的消费总额(category1-4)。其中今日总购买量 = 直接购买 + 收益，今日总赎回量 = 消费 + 转出。如果用户今日消费总量为0，则四个类目为空。

本文从申购和赎回总值的历史数据切入，分析各数据的处理方式。

2 方法描述

本文提出的资金流入流出预测模型的架构图如图1所示,整个模型包括数据预处理、序列转换、模型识、模型检验和建模预测五个关键环节。

图1 资金流入流出预测模型的构建流程

其中，数据预处理包括异常值剔除、数据集成化，序列转换包括平稳性检验、差分变换和白噪声检验，模型识别包括自相关图识别定阶和BIC准则参数估计，模型检验包括德宾-沃森检验和Ljung-Box随机性检验。

2.1 数据预处理

在明确题目背景后，本文对数据进行了预处理操作。首先是数据清洗，余额宝的用户众多，每位用户的价值也都不同。整体上看数据较为干净，没有缺失值。本文剔除14个月中总操作数少于5次或总申购值和赎回值都小于10的用户。

单个用户的个体行为随机性较强，具有不稳定性，波动大，且个体行为不具有规律性，受外界因素干扰较大。因此进行数据集成，汇总多个用户的数据以进行共同建模。本文采用全体用户以天为单位的总申购值和赎回值数据，计算全体用户427天的历史数据，获取申购值和赎回值以天为单位的时间序列图，如图2所示。

图2 用户申购和赎回的时间序列图

由图2可发现整体数据具有以下显著特点：(1)具有一定的周期性;(2)工作日和节假日有所差别，工作日比节假日高;(3)前期低，中期过高，后期逐渐进入平稳阶段，趋于平缓。因此可采用时间序列方法进行训练学习[6]，预测未来序列趋势以预测每天的申购和赎回值。

2.2 序列转换

序列转换主要包括三个环节：平稳性检验、差分变换和白噪声检验。

首先从定性的角度分析时序图，如果时序图中的序列值始终在一个常数附近随机波动，且波动的范围有界，则时间该序列为平稳序列；如果有明显的趋势或周期性，则通常为不平稳序列。若是不平稳序列，可采用差分方法对原始序列先进行一阶差分，再返回平稳检验阶段直至通过。显然余额宝资金的流入流出序列为不平稳序列。从定量的角度分析，作单位根ADF检验，计算其中的pvalue值，判断其平稳性高低。

本案例的一阶差分序列的时间序列图如图3所示。

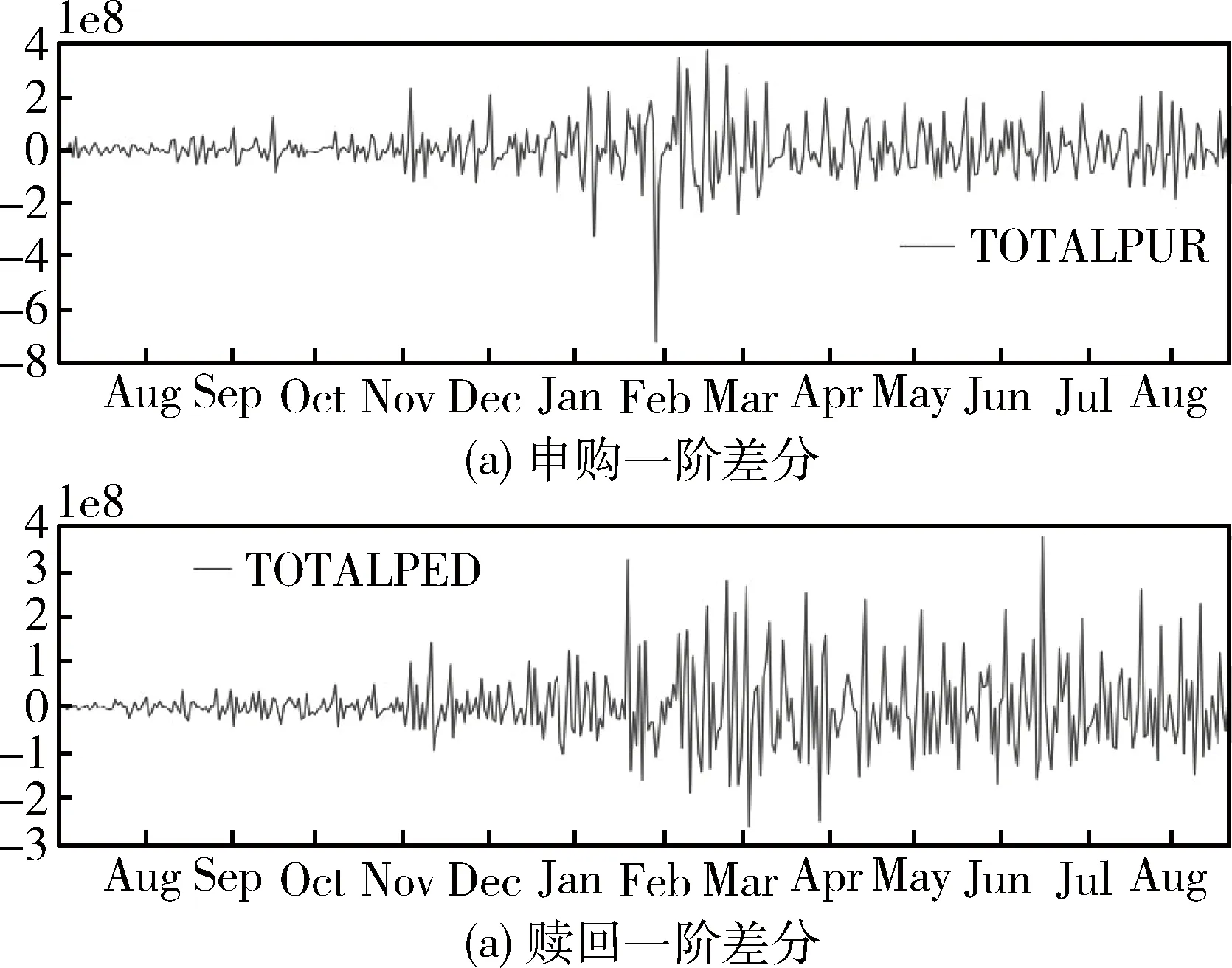
图3 用户申购和赎回的一阶差分时间序列图

随后采用Ljung-Box(LB)统计量进行白噪声检验，衡量序列的信息包含度。如果序列检验为白噪声序列，则说明序列中有用的信息已被提取完毕，剩余为随机扰动，该部分没有预测的必要。如果是平稳非白噪声序列，则可以对其建模分析[7]。本案例的详细算法如下。

算法1：序列转换算法

输入：非平稳的时间序列数据集Xt

(1)作时序图，进行平稳性趋势分析。

(2)计算单位根ADF，根据pvalue判断序列的平稳性检验。若pvalue<0.5则是平稳序列，跳至第(4)步；若pvalue≥0.5则是不平稳序列，至第(3)步进行处理。

(3)计算该序列的一阶差分DIFF(Xt)，再跳回第2步进行平稳性检验。

(4)白噪声检验，利用LB统计量检验，求得对应p值，当p<0.05则是非白噪声序列；当p≥0.05则是白噪声序列，需要进行数据的重新整合。

(5)结束

2.3 模型识别和参数估计

上述分析显示，金融数据序列的趋势具有一定的周期性，当确定其差分序列为平稳非白噪声序列后，可以选择合适的时间序列模型进行拟合[8]。

第一步是模型识别。从探索当前序列的自相关性来初步识别，根据当前序列的自相关图和偏自相关图判断最为贴近的时间序列模型。常用的时间序列模型有AR(p)模型，MA(q)模型，ARMA(p,q)模型和ARIMA(p,d,q)模型。可以参照表1识别模型。

表1 时间序列模型识别参照原则

AR(p)模型为p阶自回归模型，序列为：

xt=φ0+φ1xt-1+φ2xt-2+…+φpxt-p+εt

(1)

即在t时刻随机变量Xt的取值xt是前p期xt-1,xt-2,…,xt-p的多元线性回归，其中认为xt主要受过去p期的序列值的影响。误差项是当期的随机干扰εt，为零均值白噪声序列。

MA(q)模型是q阶自回归模型，序列为：

xt=μ+εt-θ1εt-1-θ2εt-2-…-θqεt-q

(2)

即在t时刻随机变量Xt的值xt是前q期的随机扰动εt-1,εt-2,…,εt-q的多元线性函数，其中认为xt主要是受过去q期误差项的影响。误差项是当期的随机干扰εt，为零均值白噪声序列，μ是序列{Xt}的均值。

ARMA(p,q)模型是自回归移动平均模型，序列为：

xt=φ0+φ1xt-1+φ2xt-2+…+φpxt-p+εt-θ1εt-1-θ2εt-2-…-θqεt-q

(3)

即在t时刻随机变量Xt的取值xt是前p期xt-1,xt-2,…,xt-p和前q期εt-1,εt-2,…,εt-q的多元线性函数，误差项是当期的随机干扰εt，为零均值白噪声序列，xt主要是受过去p期的序列值和过去q期误差项的共同影响。

ARIMA(p,d,q)模型是对非平稳序列的拟合，需要进行d阶差分运算，然后和ARMA(p,q)模型组合。本文的余额宝序列为非平稳序列，经差分处理后平稳，且受前期序列和误差项的影响，因此跟ARIMA(p,d,q)最为贴近。

第二步是BIC准则模型定阶和参数估计。利用BIC准则进行参数寻优的目标是寻找包含最少自由参数且能够最好地解释数据的模型。虽然增加自由参数可以提高拟合的优良性，但为避免过拟合，优先考虑的模型是使得BIC值最小的模型。定好d阶差分后，利用BIC准则找到ARIMA(p,d,q)模型对应的p,q值[9]。

2.4 模型检验

在模型识别和参数估计后，可利用初步得到的ARIMA模型对历史数据训练并预测，并将结果和真实值对比得到残差。模型检验目的是对模型适合程度进行检验：若检验通过则表示该模型可以较好地刻画序列，若检验不通过则表示该模型并不符合序列趋势，需要采用其他模型重新建模[10]。

模型检验分为三个步骤，首先使用QQ图，验证残差数据是否符合正态分布[11]。其次，对残差序列做德宾-沃森(D-W)检验，验证是否有自相关性。最后对残差作Ljung-Box(LB)检验，这是对随机性的检验，对时间序列是否存在滞后相关的统计检验。LB检验是基于一系列滞后阶数，判断序列的总体的相关性或者随机性的存在。若LB检验残差序列是高斯白噪声序列，则检验模型通过[12]。具体步骤如下。

输入：残差数据集Qt

输出：模型通过检验或不通过

(1)作QQ图，看是否正态分布。

(2)德宾-沃森检验。根据D-W值判断残差序列的自相关性。若D-W值接近0或者4，则是存在自相关性；若D-W值接近2，则无自相关性。

(3) Ljung-Box检验。计算残差序列对应的p值，若p>0.05则是高斯白噪声序列，通过模型检验，说明残差和零相差无几；若p≤0.05则是非白噪声序列，不通过模型检验，需要尝试其他模型拟合。

(4)结束。

2.5 建模预测和模型评价

在模型检验后，可采用通过的模型进行训练预测，并建立误差评价指标评价预测效果。

针对预测误差，本文比较回归预测的值Ypre与真实值Y，用均方根误差RMSE作为验证模型好坏的指标。

(4)

对于用户申购的预测误差RMSEpur和赎回的预测误差RMSEred，根据案例问题要求的重要性不同，最终的总误差评价指标为 ：

RMSEtotal=0.45RMSEpur+0.55RMSEred

(5)

3 实验结果与分析

3.1 实验流程

本文以蚂蚁金服公司余额宝资金为应用背景，数据来源是余额宝用户的真实数据。该数据集包含共28 041名用户从2013-07-01到2014-08-31共427天的2 840 421条数据操作记录。其中申购和赎回值单位是分。预测数据的单位也需精确到分。考虑测试集为2014-09的数据，无真实值对照，故选择训练集中已知的1个月作为测试集进行实验。

纵观申购和赎回值的时间序列图，发现7月、8月无节日，且处于暑假阶段，与9月情形不相似。而4月的波动情况与9月很类似，且分别包含节日清明节、中秋节，可作测试集进行实验。那么可取2013-07-01至2014-03-31的274天的样本，用上述方法预测出结果，用均方根误差进行模型评价。

3.2 实验结果与分析

如前所述，本文的资金流入流出预测模型包括数据预处理、序列转换、模型识别，模型检验、建模预测这五个主要步骤。本文对每一步数据处理产生的实验结果进行展示和分析如下。

由原始序列经过一阶差分的序列DIFF(Xt)进行平稳性检验，得到pvalue=3.419e-19。经过白噪声检验，得到p=2.787e-13。说明该案例的一阶差分模型是平稳非白噪声序列，可以进行建模。作一阶差分序列的自相关图和偏自相关图如图4、图5所示。

图4 用户申购和赎回一阶差分的自相关图

图5 用户申购和赎回一阶差分的偏自相关图

由实验结果发现申购和赎回序列符合ARIMA(p,1,q)模型，一阶差分序列是p阶拖尾，q阶拖尾。对于申购序列和赎回序列利用BIC准则进行参数估计，当调整p,q的取值范围时，得到最优值列表，分别如表2和表3所示。

参数确定后即得到初步模型，则需进行模型检验，以ARIMA(2,1,1)模型对申购序列预测为例，作残差QQ图如图6所示。对于三个不同参数的模型分别做德宾-沃森检验和Ljung-Box检验, 判断是否通过检验，结果如表4和表5所示。

图6 ARIMA(2,1,1)预测的残差QQ图

表2 申购序列p, q的取值范围下的最优值

表3 赎回序列参数p, q的取值范围下的最优值

表4 申购序列不同p, q的参数模型检验结果

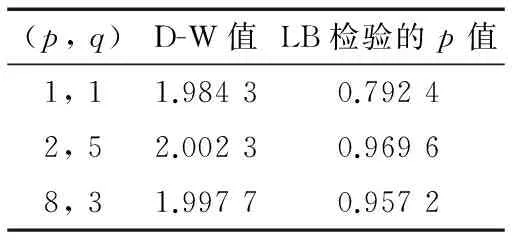
表5 赎回序列不同p, q的参数模型检验结果

由上述表格知，申购的三个模型和赎回的三个模型都通过了检验，可以较好地刻画序列，用于趋势预测。现将ARIMA(p,d,q)模型不同的p,q值参数代入，进行实验并对比预测效果，结果如表6和表7所示。

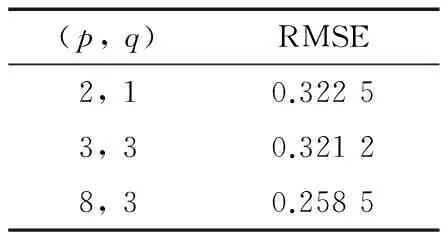
表6 申购序列不同p, q值的预测效果对比

表7 赎回序列不同p, q值的预测效果对比

综合可知，将申购和赎回序列预测的最优效果相结合，可以得到最优的最终预测效果RMSEtotal=0.45×0.258 5+0.55×0.328 2=0.296 8。本文提出的时间序列的资金流入流出预测模型取得的最优预测效果为RMSE=0.296 8。

4 结论

本文针对金融公司资金流入流出的预测问题进行研究，对减小资金流动性风险、提升资金利用效率有重要意义。以蚂蚁金服公司余额宝资金为例，针对资金数据波动性大、噪声多等特点，本文提出了基于将非平稳序列转换为平稳序列，再逐步模型识别和参数估计，经模型检验后找到合适的时间序列模型ARIMA(p,d,q)拟合，可以应用于大多数的资金流入流出预测问题。

在后续研究中，将尝试对时间序列进行分解，用加法模型和乘法模型分离季节因素，对不同分段序列选用合适的时间序列模型拟合，最后综合各段序列的预测结果成为最终结果。

[1] SOOFI A S, Cao Liangyue. Nonlinear Forecasting of Noisy Financial Data[M]. Modelling and Forecasting Financial Data. Springer US, 2002,2:455-465.

[2] FINANCE A. Multivariate nonlinear analysis and prediction of Shanghai stock market[J]. Discrete Dynamics in Nature & Society, 2008, 2008(1):47-58.

[3] Dai Wensheng, WU J Y, LU C J. Combining nonlinear independent component analysis and neural network for the prediction of Asian stock market indexes[J]. Expert Systems with Applications, 2012, 39(4):4444-4452.

[4] DAIGO K, TOMOHARU N. Stock prediction using multiple time series of stock prices and news articles[C]. Computers & Informatics, IEEE, 2012:11-16.

[5] 刘彬, 王红蕾. 贵州电网短期负荷时间序列的混沌性仿真检验[J]. 微型机与应用, 2010, 29(17):88-90.

[6] 马超红, 翁小清. 时间序列早期分类综述[J]. 微型机与应用, 2016, 35(16):13-15.

[7] Liu Xiaohong. The Statistical Test for Stationarity of Time in ARIMA Model and its Application[J]. Chinese Journal of Health Statistics, 1998.

[8] Zhang Le, Zhang Jianmin, Du Xiangge. Applying the season time series model to forecast the greenhouse daily humidity[J]. Northern Horticulture, 2008.

[9] Huang Yan, Yi Dong, Tiao Kaocong. The SAS procedure of ARIMA model and its application in time series[J]. Laser Journal, 2007, 28(1):96-96.

[10] Wang Jifang, Fei Renyuan, Xu Xiaoli, et al. Combination of ARIMA and RBF model and its application in equipment running condition prediction[J]. Journal of Mechanical Transmission, 2011, 35(9):85-87.

[11] 张玲, 刘波. 基于残差统计的时间序列加性离群点检测算法研究[J]. 电子技术应用, 2015, 41(9):85-87.

[12] 张良均．Python与数据挖掘[M].北京：机械工业出版社，2016.

A prediction model of funds inflow and outflow based on time series algorithm

Cao Can, Huang Hai, Xu Ke

(School of Information Science and Technology, University of Science and Technology of China, Hefei 230027, China)

It is great significant to reduce the liquidity risk of the network financial platform and improve the funds utilization rate to predict funds inflow and outflow. In this paper, we research on predicting Ant Financial Services Group YuEBao funds inflow and outflow in next 30 days according to historical records. Because historical data is instable with much noise, we utilize the differential conversion method to transfer the original sequences to stable sequence. Then, though the model identification and parameter estimation we obtain a preliminary model. Next we select the suitable time series model to predict the residual sequence and do model check. At last, we use the approved model trains data to predict final results. The results of experiments verify that the proposed prediction model can effectively predict the funds inflow and outflow.

funds inflow and outflow prediction; sequence transfer; parameter estimation; time series model

TP181

A

10.19358/j.issn.1674- 7720.2017.14.017

曹璨，黄海，徐可.一种基于时间序列算法的资金流入流出预测模型[J].微型机与应用，2017,36(14)：52-56.

2017-01-26)

曹璨(1992-)，女，硕士，主要研究方向：数据挖掘。

黄海(1980-)，男，博士，副研究员，主要研究方向：机器学习，数据挖掘。

徐可(1995-)，男，硕士，主要研究方向：数据挖掘。