基于变增益PID控制的起重机防摇摆设计与仿真

郭瀛舟，郑建立

(东华大学 信息科学与技术学院，上海 201620)



基于变增益PID控制的起重机防摇摆设计与仿真

郭瀛舟，郑建立

(东华大学 信息科学与技术学院，上海 201620)

以防摇系统装置的小车为控制对象，对防摇模型的相应受力情况进行分析，建立小车的动力学模型，设计了基于比例积分微分(PID)和状态反馈的控制器。通过Simulink对模型系统进行了验证和仿真，得到PID的最优控制参数，最后通过编程，在实际装置上实现了对小车的防摇控制。实验结果表明，变增益PID控制器能够实现小车的迅速消摆。

防摇系统；运动控制；系统模型；状态反馈

0 引言

在集装箱运输业中，码头常见的起吊装置有桥吊、门吊等设备。在装卸过程，由于自身及外界原因，集装箱难免会发生摇摆现象。为了提升安全性和装卸货物的效率，经常会给相应系统加装一个防摇控制器。

近年来，国内外对防摇方法的研究日益增多，核心问题在于实现对起吊装置大、小车的定位以及对负载的防摇控制。本文以贝加莱防摇模型实验平台为基础，使用机理建模及实验建模，利用变增益比例、积分、微分(PID)控制很好地实现了系统的防摇控制[1-2]。

1 实验平台及模型建立

1.1 实验平台简介

本文使用的防摇模型由贝加莱工业自动化有限公司设计。它安装固定在特制电气柜中，主要由同步电机、直线导轨、摆锤三部分组成，通过电机带动小车在导轨上移动，实现对摆锤的运动控制。该模型使用贝加莱伺服驱动器控制步进电机，通过履带带动小车在直线导轨上移动。小车单摆上装有编码器，用来检测摆锤位置。装置的控制面板能很好地进行小车运动控制。该模型硬件设备主要包括可编程逻辑控制器(PLC)、ACOPOSmicro伺服驱动器、配套的电源模块、电机及其他配件,如：开关、设备框架、限位开关、寻参开关、导轨、摆锤、编码器等。

1.2 模型建立

从控制的角度来看，过程的静态数学模型是系统方案和控制算法设计的基础；然而，在很多情况下要求把静态模型和动态模型结合起来[3]。

1.2.1 机理建模

图1 防摇控制系统抽象模型

起重机防摇系统是很复杂的系统，除了系统本身器件的非线性外，还有来自外界的不确定因素的影响，比如摩擦力、风力等。结合本文研究对象，为抓住重点，对该系统做必要简化后[4]得到如图1所示的模型。

利用拉格朗日力学对系统进行受力分析可得到起重机定位与防摆控制系统的非线性动力学微分方程：

(1)

为了研究方便，将不考虑负载的提升，即在定绳长条件下进行定位与防摆控制研究。考虑到负载摆角一般不超过10°，可近似为sinθ=0，cosθ=1：，则系统简化的线性化方程如下：

(2)

对式(2)进行拉普拉斯变换后整理得：

(3)

整理得到传递函数：

图2 起重机模型角度与速度曲线

(4)

将(3)式写成状态空间的形式：

(5)

则有:

(6)

由以上可得：

(7)

由系统的状态方程可知，起重机吊运系统是一个强耦合、非线性以及参数可变的复杂研究对象。吊重的摆角大小受小车加(减)速度的影响比较大，会随着小车加(减)速度的增大而增大；小车在加减速阶段，摆角及其加速度会发生突变，且呈现非周期性的变化。

1.2.2 实验建模

本质上来说，通过机理分析建立的模型是线性化近似模型，在一些情况下如摆杆角度大时不能反映系统的非线性特效，需要采用更好的方式来建立模型。所以接下来将以贝加莱防摇起重机为实验对象，采用辨识来建立起重机系统的非线性系统模型。本实验建模的设计是在贝加莱公司提供的硬件设备及软件demo的基础上完成的。软件demo是antisway_demo_hardware_0719。在软件demo的基础上添加系统控制器、控制算法实现电机控制的摆锤稳定运行。

在贝加莱提供的Automation Studio(AS)软件及VNC软件的仿真环境下，采集起重机的输入输出数据。在AS软件中，打开封装的VNC模型变量进行监视，将使能“Enable”置1，然后给定速度“SetTrolleyVelocity”一个初值，记录起重机模型摆角及速度曲线。例如，给定一个初速度SetTrolleyVelocity=5作为实验建模的激励信号，得到相应的摆角及速度曲线，如图2所示。

将激励信号“SetTrolleyVelocity”模块速度从0到5(最大速度)以0.1的步长进行增长，得到50组不同速度下的摆角曲线。

观察采集到的摆角曲线样本可以发现，50组数据的摆角趋势都如同图2中的“theta”曲线，经过一系列假设及运算，推出该对象的传递函数为：

(8)

在MATLAB中求解得到两个共轭复特征根,这两个共轭复特征根的值均落在左半s平面，则说明该开环系统是稳定的，并且带有较强的震荡性。

2 PID控制器设计与仿真

2.1 常规PID控制器与微分先行控制器

常规PID控制系统原理图如图3所示。

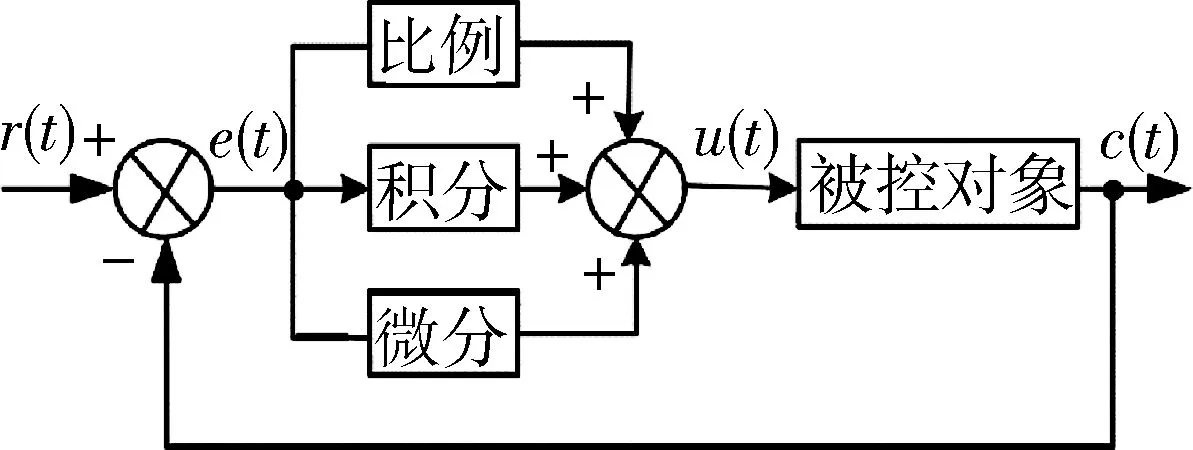
图3 PID控制系统原理图

以式(8)的模型为控制对象，将扰动信号作为输入，增加PID控制器，形成闭环系统，通过摆角输出偏差控制速度给定值，即以反馈摆角信号来消除摆动。起重机常规PID防摆系统仿真如图4所示，起重机微分先行PID防摇系统仿真图如图5所示。

图4 起重机常规PID防摆系统仿真图

图5 起重机微分先行PID防摆系统仿真图

经过反复调节Kp、Ki和Kd三个参数，得到常规PID模块的整定参数为：

Kp=100，Ki=0，Kd=20

(9)

微分先行PID模块的整定参数为：

Kp=50，Ki=0，Kd=10

(10)

2.2 变增益PID控制器

图6 变增益PID控制框图

变增益PID控制的定义应当是：在PID控制系统中的适当位置加入变增益补偿环节，使控制系统的非线性特性得到校正，从而使控制系统的动态品质保持稳定，系统框图如图6所示。图6中变增益补偿运算环节可以在PID之前加入，也可以在PID运算之后加入[5]。

实际的工艺过程中，由于控制偏差、负载、给定值、被控变量、控制变量等参数的变化引起控制系统中某环节特性参数发生变化的情况各异，因此变增益PID控制的补偿方案也形式多样，应以具体的控制对象进行选择。

3 控制系统的实现及仿真

3.1 控制系统实现概述

图7 摆杆角度的4种状态

将上节常规PID控制器、微分先行PID控制器以及变增益PID控制器分别进行C语言代码编程(AS项目“Program”→“Variables.var”(通过Watch)→“StartCtl=1”开启控制作用)，并在AS软件中实现对起重机模型的摆角控制。

在试验中，测试摆杆角度的4种状态A、B、C、D，如图7所示(规定图中在法线右边为正，箭头代表摆杆的运动方向)。

3.2 PID控制器的具体实现

经过反复试验，可以求出三个控制器防摇效果最好时，PID参数的值，分别为：(1)当θ=20°时，常规PID控制器防摇效果最好；(2)当θ=40°时，微分先行PID控制器防摇效果最好；(3)当θ=60°时，变增益PID控制器防摇效果最好。

相对于常规PID控制器和微分先行PID控制器，变增益PID控制器的控制效果更优，上升时间更短，超调量绝对值更小。

4 实验及其结果分析

将三个PID控制器模型仿真曲线放在同一坐标下进行比对，如图8所示，细节如图9所示。可以看到，三个PID控制器对起重机模型的摆角抑制作用很强，响应速度快，超调小或不超调，控制作用达到误差允许范围内的时间很短。三者相较，变增益PID控制器能更好地实现对系统稳态误差的控制。

图8 三个PID控制器模型仿真曲线对比图

图9 三个PID控制器模型仿真曲线细节对比图

5 结论

针对贝加莱防摇装置，首先进行了机理建模；然后，使用实验建模的方式，采用辨识建立了起重机系统的非线性系统模型。针对该系统，使用了三种PID控制器对系统进行控制，最后得出变增益PID控制器对起重机模型的摆角抑制作用最强，响应速度最快，超调最小，控制作用达到误差允许范围的时间最短。

[1] PRASAD L B, TYAGI B, GUPTA H O.Optimal control of nonlinear inverted pendulum system using PID controller and LQR: performance analysis without and with disturbance input[J]. International Journal of Automation and Computing,2014,11(6): 661-670.

[2] 杜文正,童国林,强宝民,等.基于模糊自适应PID控制器的桥式起重机定位与防摆控制研究[J].制造业自动化,2012,34(11):8-11.

[3] 胡艳丽.基于模糊PID的桥式起重机防摆控制研究[D].焦作：河南理工大学,2010.

[4] 李伟.起重机载荷摆振模型的简化条件及误差[J].山东建筑工程学院学报,1998,13(2):59-64.

[5] 刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社,2003.

The anti-shake system based on motion state feedback control

Guo Yingzhou, Zheng Jianli

(College of Information Science and Technology, Donghua University, Shanghai 201620, China)

In this article, we take the cart of anti-swing system device as the control object, analyze the corresponding stress of the anti-swing model, establish the dynamic model of the cart, and design the controller based on proportional integral derivative (PID) and state feedback. Verifying and simulating this model system via Simulink, we obtain the optimal control parameters of PID.Finally, we realize the anti-swing control of the car in particular device through programing. The experimental results show that the variable gain PID controller can rapidly eliminate the swing of the cart.

anti-shake system; motion control; system model; state feedback

TP393

A

10.19358/j.issn.1674- 7720.2017.14.001

郭瀛舟，郑建立.基于变增益PID控制的起重机防摇摆设计与仿真[J].微型机与应用，2017,36(14)：1-3，10.

2017-02-27)

郭瀛舟(1990-)，男，硕士研究生，主要研究方向：智能控制系统。

郑建立(1962-)，男，博士，副教授，主要研究方向：微机技术。