电动机微机保护算法分析研究*

王 伟，王静文

(1.鄂尔多斯应用技术学院 电子信息工程系，内蒙古 鄂尔多斯 017010；2.鄂尔多斯应用技术学院 土木工程系，内蒙古 鄂尔多斯 017010)



电动机微机保护算法分析研究*

王 伟1，王静文2

(1.鄂尔多斯应用技术学院 电子信息工程系，内蒙古 鄂尔多斯 017010；2.鄂尔多斯应用技术学院 土木工程系，内蒙古 鄂尔多斯 017010)

针对电动机微机保护的软件算法进行了研究，介绍了微机保护中基于正弦函数模型和基于周期函数模型的常见算法，对各算法的原理进行了阐述，通过对比被测量的计算值和实际值，比较了各算法的运算速度和滤波性能，并重点分析了其计算精度，得出傅里叶算法适用于采样计算电力系统故障量的结论，为研究和确定电动机微机保护的软件设计提供理论参考。

微机保护；算法设计；性能分析

0 引言

电动机微机继电保护算法的基本实现过程是通过对被测故障信号的采样值进行识别、计算后再进行逻辑判断和保护动作。适当的保护算法既要确保数据精度，又要使计算时间尽可能短，即程序具有准确性和快速性[1-2]。

常见的微机保护算法主要有两类：正弦函数模型算法和周期函数模型算法。第一类算法假设被采样的电压和电流量都是标准正弦信号，则实际电压和电流的幅值、相位、功率等参数可以利用正弦函数特性由采样值计算得到[2-4]。然而电动机实际发生故障时，电压和电流波形大多是基波与衰减的非周期分量及高频分量的叠加[5-7]；且数据采集系统也会引入误差，这些都会导致测量精度下降。因此在保护算法的前级需要使用数字滤波器尽可能地滤掉采样信号的非周期分量及高频分量[8-10]。基于周期函数模型算法中最常用的傅里叶算法，由于具有滤除高次谐波的功能，因此可以有效地削弱谐波成分，且简化了程序量[8-10]。

1 保护算法设计

1.1 两点乘积法

假设标准正弦交流电压和电流函数表达式如下：

(1)

对其进行相隔90°(ΔT=T/4)采样，得到两组采样值为：

(2)

(3)

对式(2)和式(3)运算得：

(4)

得到常用的被测量表达式：

(5)

由式(5)可知，电路中电压、电流的有效值以及有功功率和无功功率可通过计算电路在任意时刻进行相隔T/4的电压和电流采样值得到。对工频交流电来说，两点采样法的数据窗宽度应为T/4=5 ms。

1.2 均方根法

对于周期为T的标准正弦信号来说，电压有效值、电流有效值及平均功率的定义如下：

(6)

设采样从t=0时刻开始，在一个周期T内均匀采样N个数据点，记n点处的电压和电流采样值为Un、In[11-13]。故将式(6)离散化后可得离散计算公式：

(7)

由于计算结果是均方根值，因此当采样数据点较多时，均方根法对畸变波形也适用[6]。

1.3 半周积分法

在任意半周期内，标准正弦量绝对值的积分是固定值，与初相角无关，设这个固定值为常数X，如图1所示，图中两块面积S显然是相等的[10-11]，即

(8)

由(8)式可以看出，X与幅值Um成正比例关系，因此可用梯形法来近似半周积分法，原理如图2所示。

即半周期积分算法可近似用梯形法等效为下式：

(9)

图1 半周期积分原理

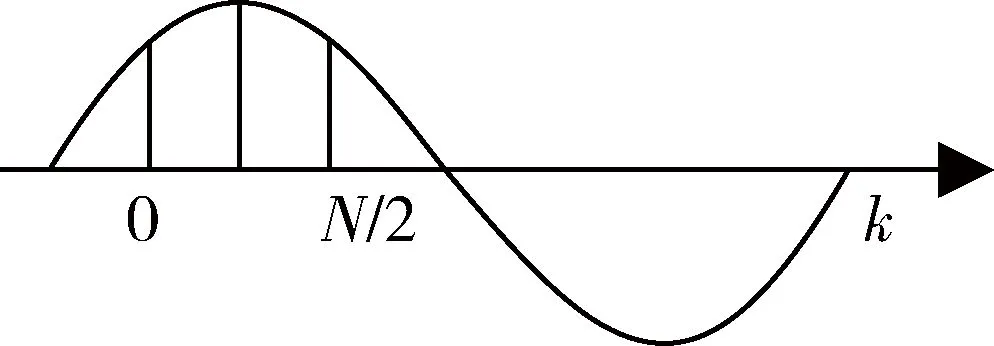
图2 梯形法近似半周期积分图

式中：X为半周期内k个采样值的总和；Ui为第i个采样值，且Ui=Umsin[α+ω(i-1)Ts]；k为半周期采样数；α为第一个采样值的初相角；K(α)为X与Um比值。

输入已知幅值的标准正弦波后便可测出K(α)值，这样就可以通过采样值和K(α)计算出实际被测波形的幅值。由于用采样值求和代替了连续的积分值，因此K(α)的计算会有误差，且该误差与α值有关。当N值不变时，K(α)仅随α变化，表1给出了ωTs=30°、N=12时，K(α)和α值的变化规律。

表1 K(α)的值随初相角α值的变化

同理，可求出电流幅值Im，进而可计算阻抗值Z：

(10)

1.4 导数法

导数法是利用输入正弦量在某一时刻t1的采样值和采样值的导数计算出被测量有效值和相位的算法。

设正弦电压u、电流i在t1时刻的采样值为：

(11)

则t1时刻的导数值为：

(12)

联立式(11)、(12)可以求得：

(13)

实际编程时，可以利用t1时刻相邻的采样数据点值来近似计算t1时刻电压和电流导数，其原理如图3所示。

图3 导数法原理图

即t1时刻电流、电压导数值为：

(14)

1.5 傅里叶算法

傅里叶算法利用傅里叶变换提取被测量中某一频率的信号分量。对于周期性被测量可展开成傅里叶级数，形式如下：

犍为县食品药品监督管理局始终坚持“严”字当头、守土把关，全面落实“四有两责”，管控好老百姓“舌尖上”的安全，监管工作连续多年综合排名乐山市第一。该局先后荣获“市级先进单位”“市级文明单位”“市级学法用法示范单位”“省级卫生单位”等称号，2016年9月被评为“四川省食品药品监督管理系统先进集体”，跻身全省县级局前列。

(15)

式中，n为自然数，n=0，1，2…；an、bn为各谐波成分的正弦项和余弦项幅值。根据傅里叶级数原理，可以求出a1、b1分别为：

(16)

则x(t)中的基波分量为：

x1(t)=b1cosω1t+a1sinω1t

(17)

经三角变换后可写为：

(18)

其中，X为基波分量的有效值；φ1为t=0时基波分量的初相角。

将sin(ω1t+φ1)用和角公式展开后与式(17)对比可得a1、b1与X、φ1的关系为：

(19)

故可根据a1和b1求出有效值X和相角φ1关系式：

(20)

实际根据式(16)用微机计算a1和b1时，通常只取用有限项，即用采样值代入x(t)，从而将连续积分运算转化为离散数值求和运算，考虑到NΔt=T，ω1t=2kπ/N，则：

(21)

其中，N为一个周期内的采样点数；xk为第k次采样值。

同理，任意次谐波的an、bn为：

(22)

利用式(21)、(22)的方法计算一个频率分量时，计算量相当大。因此，为简化运算，提高计算速度，实际微机保护算法常采用的是递推式傅里叶算法。

设被测量一个周期内的采样数为N，则每个采样时刻的计算值为[14]：

(23)

其中，x(i+m-N)为t=(i+m-N)Ts(i=1,2,…,N)时刻的采样值；an(m)、bn(m)为n次谐波分量在m个采样点处的正、余弦项幅值。

同理，可以推出t=(m-1)Ts时刻的采样值计算公式，故有下列递推公式：

(24)

这种递推算法只需数次加减法和乘法运算，且与采样次数N的值无关，大大减少了运算量，提高了算法的运算速度[15-17]。

2 算法性能分析

通过分析微机保护各算法的原理可以定性地得到以下性能特性：两点采样法编程简单，计算速度快，但也有一些弊端，包括易受直流成分影响、无滤波性能、采样间隔精度要求高等[8]；均方根法无滤波作用，其采样数据窗为一个周期T，因此计算速度较慢；半周积分法的计算精度取决于采样点数和K(α)值的预计算精度，速度较快，由于在半周积分过程中，偶次谐波中的正负半周相消，谐波成分所占比重减少，故半周积分算法有一定滤波作用，但不能滤出全部谐波分量；导数法的快速性较好，但受直流分量影响大，由于该法是相邻点近似导数运算，故精度不高。傅里叶算法计算精度高，滤波性能好，采用递推傅里叶公式后计算量较小，具有较高实用价值。

在MATLAB/Simulink仿真环境下，直流电动机正常工作状态下和A相短路接地故障状态下的三相电流有效值的仿真值与应用以上部分算法求解的计算值进行比较，结果如图4和图5所示。

图4 正常工作状态下三相电流有效值

图5 A相短路接地故障时三相电流有效值

通过图4、图5，电动机在正常工作状态和故障状态下的三相电流有效值比较可以看出：傅里叶算法最接近真实值，均方根算法优于两点乘积算。而傅里叶算法的运算速度和滤波性能又优于均方根法，故实用性较好。

3 结束语

本文分析了电动机微机保护中常见几种算法的原理，通过仿真比较了各算法的计算精度、速度及滤波特性等性能指标，验证了各微机保护算法的可行性。傅里叶算法以其准确性、速动性和较好的滤波性能可以作为计算电动机电压、电流有效值保护算法的较实用算法。

[1] 邓东华. 微机综合测控保护技术的研究[D]. 南京：南京理工大学，2004.

[2] 薛春旭. 电力系统微机继电保护交流采样算法研究[D]. 西安：西安电子科技大学，2012.

[3] 张华. 基于双CPU的中低压线路微机测控保护装置的研究[D]. 南京：东南大学,2005.

[4] 李彦丽. 基于DSP的变压器差动保护装置的研究[D]. 天津：河北工业大学,2007.

[5] 刘美俊,胡俊达. 基于傅氏算法的智能化微机电力监控系统[J]. 电力系统及其自动化学报,2003,15(5)：83-85.

[6] 黄慧春. 基于M·CORE平台的中低压电网设备数字式综合测控保护装置的研究[D]. 南京：东南大学，2004.

[7] 曾庆军,刘阳，金升福,等.基于CAN总线的低压断路器新型可通信智能控制器研制[J].低压电器,2004,24(10)：28-32.

[8] 李建英. 新型电动机微机保护测控系统的研究与设计[D]. 长沙：湖南大学，2005.

[9] 丁祖军. 混合式电力电子断路器关键性能及短路电流快速检测方法的研究[D]. 南京：东南大学，2005.

[10] 刘春孜. 基于PROFIBUS通信的电机综合保护[D]. 长沙：湖南大学，2006.

[11] 郝婧. 基于网络的异步电机保护装置设计[D].西安：西安理工大学，2008.

[12] 高鹏飞. 基于DeviceNet的可通信电机保护器的研究[D]. 兰州:兰州理工大学，2010.

[13] 刘冰，郝庆水,丛振刚,等. 基于单片机的RTU三相交流采样技术[J]. 中国电力，2006,39(10)：88-90.

[14] 杨意，于群. 基于F410的矿井低压无功补偿控制器的研制[J]. 电气技术,2011(12):34-36,45.

[15] 钱可弹，李常青. 电力系统微机保护算法综合性能研究[J]. 电力自动化设备，2005,25(5)：43-45.

[16] 杨磊. 电力系统继电保护可靠性评估研究[D]. 保定：华北电力大学，2014.

[17] 罗洪广. 微机保护算法综合性能分析[D]. 成都：西南交通大学，2006.

Analysis and research on microcomputer-based algorithm of motor protection

Wang Wei1, Wang Jingwen2

(1. Department of Electrical Information Engineering, Ordos Institute of Technology, Ordos 017010, China; 2. Department of Civil Engineering, Ordos Institute of Technology, Ordos 017010, China)

The algorithm of microcomputer protection for motor is studied. Some common algorithms in microcomputer-based protection are introduced, which are mainly divided into two categories: the sine function model algorithm and the periodic function model algorithm. The principle of each algorithm is expounded. By comparing the calculated value of each algorithm and the actual value, the calculating speed and filtering performance are listed, and the calculation precision is analyzed emphatically. It is concluded that Fourier algorithm is a suitable method for fault quantity sampling calculation of power system. It provides a theoretical reference for software research and design of the microcomputer-based protection.

microcomputer-based protection; algorithm design; performance analysis

内蒙古自治区级大学生创新创业训练项目基金(201614532004)

TP311.11

A

10.19358/j.issn.1674- 7720.2017.14.006

王伟，王静文.电动机微机保护算法分析研究[J].微型机与应用，2017,36(14)：16-19，22.

2017-02-19)

王伟(1989-)，男，硕士，讲师，主要研究领域：电机控制技术。

王静文(1991-)，女，硕士，讲师，主要研究领域：结构工程。