基于改进小波阈值去噪的图像增强算法*
刘 冰,刘雪梅
(1. 达州职业技术学院,四川 达州 635001; 2. 西南大学 计算机与信息科学学院,重庆 400715; 3. 四川省达州市统计局,四川 达州 635000)
基于改进小波阈值去噪的图像增强算法*
刘 冰1,2,刘雪梅3
(1. 达州职业技术学院,四川 达州 635001; 2. 西南大学 计算机与信息科学学院,重庆 400715; 3. 四川省达州市统计局,四川 达州 635000)
针对传统小波阈值去噪算法容易导致重构信号出现附加的振荡和阈值处理前后存在恒定偏差的情况,提出了一种新的阈值去噪算法:在第n层小波变换阈值λn两侧分别取一正值a,b,使得小波系数的绝对值在a,b处连续且一阶可导,旨在增强阈值的灵活性。实验表明,去噪效果较传统方法更加高效。同时,在此基础上,选择对比度图像增强技术来进一步提升含噪图像分割质量。通过仿真实验,运用传统方法和本文改进算法分别对附加了高斯噪声和随机噪声的图像进行处理,结果表明,本文改进算法在信噪比和峰值信噪比数据上都具有明显的优势。
小波变换;阈值去噪;灰度变换;信噪比;峰值信噪比
0 引言
在获取、传送和转换图像的过程中,受环境条件和电气系统等的影响与限制,在所获得图像的视觉效果和识别方便性等方面往往不如预期,存在诸多的问题。尽管不同主体对图像质量的评判标准有所差异,但对进一步改善图像质量却是人们的普遍需求。
为了能更好地检测和测量特定图像中感兴趣的目标,有必要对所获得的图像进行去噪和增强处理,使其能转换成为一种更适合于人眼观察或计算机进行分析处理的形式。其基本原理是:一方面,减弱或去除不需要或不重要的信息,另一方面,增强处理图像中需要的信息[1]。
当前,增强处理技术已经在诸如医学检测、航空航天、指纹识别、无损探伤等多个领域中得到应用。例如医生通过对增强处理了的相关医学图片进行分析,能更精准地探清病变的情况;军事侦察人员通过对增强处理了的红外图像进行分析,能有效地发现敌方极其隐蔽的目标等。
在图像处理过程中,图像去噪和图像增强是两个十分重要环节。本文将在分析传统的小波阈值去噪算法的基础上,给出一种改进的去噪算法,并运用对比度图像增强技术来实现原始图像的有效分割。
1 图像去噪原理及相关算法
设f(i,j)表示含有噪声的远程小目标图像,s(i,j)表示含有小目标的原始图像,n(i,j)为噪声。其数学模型如下表示:
f(i,j)=s(i,j)+n(i,j)
(1)
小波是近年来发展起来的一种时频分析工具,它在分离相关性较强的数据方面具有独特的优势。在这之前,对于图像的降噪大多采用低通滤波器直接滤除高频信息的方法来实现,但由于阈值设定缺乏灵活性,一些有用的高频信息也会随着噪声的去除而丢失。而采用小波进行去噪,由于其多分辨率特性,它用不同中心频率的带通滤波器对信号进行滤波,把主要反映噪声频率的小波系数去掉,再把剩余的小波系数结合起来进行重构,从而使得噪声得到很好的抑制[2]。
目前,在图像去噪领域出现了许多基于小波的算法,其中较为著名有:(1)小波分解与重构快速算法(Mallat算法)[3-4],该方法将含有噪声的图像在某一尺度下分解到不同的频带内,然后将噪声包含的频带置零并进行小波重构,达到图像去噪的目的,但该算法要求信号较长,在实际使用中存在一定限制[5];(2)小波变换模极大值法[6-7],该方法是根据原始图像与噪声在奇异性上存在一定的差异,运用多分辨思想,通过由粗及精地跟踪各尺度下的小波变换极大值来进行噪声的消除,该方法去噪后能很好地保留反映信号特征的奇异点信息,去噪后的信号没有多余震荡,能得到较高的信噪比,但该方法主要适于信号中混有白噪声且含有较多奇异点的情况,且计算复杂,运算速度也非常慢;(3)小波阈值去噪算法[8],该算法主要运用含噪图像在经过小波变换后,原始图像和噪声的能量分布存在差别的特点来进行噪声的去除,该算法影响较大,出现了许多改进的算法,本文将在分析该算法的基础上,提出一种新的改进算法。
2 传统小波阈值去噪算法
根据DONOHO D L的算法思想[9],小波阈值去噪法的基本步骤为:
(1)选择适当的小波并确定小波分解的层数j,计算出含噪图像的小波分解系数;
(2)对每层系数选择一个恰当的阈值,并对高频系数进行处理;
(3)对处理后的小波系数进行小波重构,即为去噪后的原始图像信息。
2.1 硬阈值法和软阈值法

(2)
软阈值去噪算法的数学模型为:
(3)
其图形如图1所示。

图1 传统阈值去噪函数曲线图
2.2 存在的问题
3 改进小波阈值去噪法
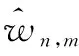
(4)
在式(4)中,δ(x)=Ax3+Bx2+Cx+D,且满足:δ(a)=0,δ′(a)=0,δ(b)=b-λn,δ′(b)=1。
由此不难得到三次多项式δ(x)的各项系数的值:
(5)
根据上述分析不难发现,对于λn两侧不同的a,b值,其处理结果也会不同,这为灵活处理图像提供了较大的可能性,如果a,b的取值适当,将会极大地提升图像的去噪效果。
4 图像增强
通过上节的改进算法虽然能够很好地重构出原始图像,但总有部分原始图像和噪声的小波系数被设定的阈值错误地去除,重构图像中仍会存少量的干扰和部分噪声。本节将在上一节的基础上采用灰度变换的图像增强技术来进一步提升图像质量。
目前较为流行的图像增强技术主要有对比度增强、直方修正分析和图像间的相互运算等几种增强技术[14]。本文选择对比度增强技术,并分别用线性变换和非线性变换来处理。
4.1 线性灰度变换
如果原图像f(x,y)的灰度范围是[a,b],希望变换后的图像g(x,y)的灰度范围线性地扩展至[c,d],则对于图像中的任一点的灰度值进行如下的变换:
(6)
如果图像中只有极少部分的灰度级超过区间[a,b],则可将式(6)改进为:
g(x,y)=c,o≤f(x,y)≤a

d,b≤f(x,y)≤max(f)
(7)
其中,max(f)为原始图像的最大灰度级。对于过度曝光或曝光不足的图像,其灰度层级往往较窄,这时采用线性变换对图像中的像素进行线性拉伸,能更加有效地改善图像视觉效果。
若要更为精细地调整图像的对比度,最大程度地改善图像质量,可对不同的灰度段做不同的调整,这时,可设计如下的分段线性变换来进行处理:
(8)
式中,k1,k2,k3表示其所在直线段的斜率。其变换图形如图2所示。
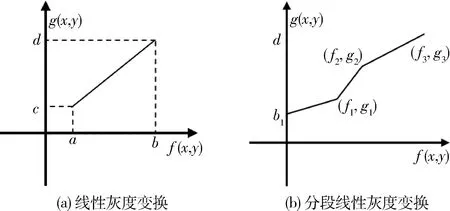
图2 线性灰度变换图
4.2 非线性灰度变换
非线性变换即是利用非线性变换函数对图像进行灰度变换,常用的变换有对数变换和指数变换。
对数变换:指图像的输出与输入的对应像素点的灰度值之间为对数关系,常用来扩展低值灰度,压缩高值灰度,适用于过暗的图像。其一般表达式如下:
g(x,y)=a+ln(f(x,y)+1)·(blnc)-1
(9)
其中,a,b,c为可选择参数。
指数变换:指图像的输出与输入的对应像素点的灰度值之间为指数关系,常用来扩展高值灰度,压缩低值灰度,适用于过亮的图像。其一般表达式为:
g(x,y)=bc×[f(x,y)-a]-1
(10)
其中,a,b,c为可选择参数。当f(x,y)=a时,g(x,y)=0,此时指数曲线交于X轴,由此可见参数a决定了指数变换曲线的初始位置,参数c决定了变换曲线的陡度,即决定了曲线的变化速率。
5 实验结果及其评价
为了验证本文提出的改进方法的有效性,在实验中结合采用传统的小波阈值去噪法,对某256×256像素的灰度图像分别添加高斯白噪声和随机噪声,在MATLAB软件上进行仿真处理,并比较相关的处理结果。其中,计算机硬件配置为:酷睿双核、主频2.0 GHz的CPU,4 GB的内存;计算机软件配置为:Windows 7.0操作系统,小波函数选择sym8。实验结果显示,改进算法的去噪效果优于传统的软阈值和硬阈值方法。表1显示了三者在分别处理含有高斯噪声和随机噪声图像时其处理结果的信噪比和峰值信噪比的对比情况。
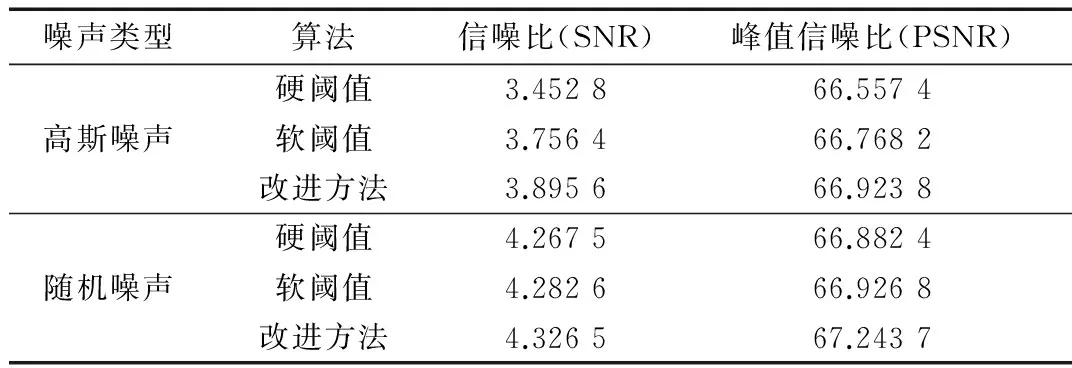
表1 各算法处理后的信噪比、峰值信噪比对照表
6 结论
本文分析了传统小波阈值去噪算法存在的容易导致重构信号出现附加的振荡和阈值处理前后存在恒定偏差的问题,在此基础上,为了增强阈值的灵活性,构造了一个新的阈值去噪函数,该函数的关键之处在于选取合适的a,b。其具体作法是:在第n层小波变换阈值λn两侧分别取一正值a,b,使得小波系数的绝对值在a,b处连续且一阶可导。实验表明,去噪效果较传统方法更加高效。同时,为了更进一步提升含噪图像分割质量,本文选择对比度图像增强技术来改善图像质量。通过仿真实验表明,运用传统方法和本文改进算法分别对附加了高斯噪声和随机噪声的图像进行处理,本文提出改进算法在信噪比和峰值信噪比数据上都具有明显的优势。
[1] GONZALEZ R C, WOODS R E.数字图像处理(第三版)[M].阮秩琦,阮宇智,等,译.北京:电子工业出版社,2011.
[2] 王晅,马建峰.数字图像处理与模式识别[M].北京:科学出版社,2011.
[3] 李建平,唐远炎.小波分析方法的应用[M].重庆:重庆大学出版社,2000.
[4] 张旭东,詹毅,马永琴.不同信号的小波变换去噪方法[M].北京:石油地球物理勘探,2007.
[5] 韦力强.基于小波变换的信号去噪研究[D].长沙:湖南大学,2007.
[6] MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J]. IEEE Transaction on Information Thecry, 1992,38(2):617-643.
[7] DONOHO D L. Denoising via soft thresholding[J]. IEEE Transaction on Information Theory, 1995,41(3):613-627.
[8] 张臻,于海勋.光线缺陷的超声信号小波阈值去噪改进算法[J].NDT无损检测,2008,30(12):895-897.
[9] DONOHO D L, JOHNSTONE I M. Adapt to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432):1200-1224.
[10] 陶红艳,秦华峰,余成波.基于改进阈值函数的小波域去噪算法的研究[J].压电与声光,2008, 30(1):93-95.
[11] 王成,黄玉清.基于小波分解的分层自适应图像增强[J]. 微型机与应用,2015, 34(23):37-40.
[12] 倪培峰,胡雄.一种基于改进阈值函数的小波阈值降噪算法[J].电子技术应用,2016,42(8):98-100.
[13] 朱艳芹,杨先麟.几种基于小波阈值去噪的改进方法[J].电子测试,2008(2):18-22.
[14] 张德丰.详解MATLAB数字图像处理[M].北京:电子工业出版社,2010.
An image enhancement algorithm based on improved wavelet threshold denoising
Liu Bing1,2, Liu Xuemei3
(1. Dazhou Vocational and Technical College, Dazhou 635001, China; 2. College of Computer and Information Science, Southwest University, Chongqing 400715, China; 3. Statistics Bureau of Dazhou City, Sichuan Province, Dazhou 635000, China)
A new threshold denoising algorithm is proposed to resolve the problems of traditional wavelet threshold de-noising algorithms, which may lead to additional oscillations of reconstructed signals and constant bias before and after threshold processing. In this methodaandbare respectively taken on both sides of the threshold value of wavelet transform layernso that the absolute values of the wavelet coefficients are continuous and first order derivable ataandb. Its purpose is to enhance the flexibility of the threshold. Experiments show that the denoising effect is more efficient than the traditional method. At the same time, contrast image enhancement technique is selected to improve the quality of noisy image segmentation. The simulation results show that the proposed algorithm has obvious advantages in both SNR and SNR data, by using the pass-through method and the improved algorithm, respectively, to deal with the image with Gaussian noise and random noise.
wavelet transform; threshold de-noising; gray-scale transformation; SNR; PSNR
四川省教育厅重点科技计划项目(14ZA0330); 四川省达州市2014年科技计划项目(2014-8220)
TN219
A
10.19358/j.issn.1674- 7720.2017.14.013
刘冰,刘雪梅.基于改进小波阈值去噪的图像增强算法[J].微型机与应用,2017,36(14):39-42.
2017-01-20)
刘冰(1970-),男,副教授,主要研究方向:信息安全、图像处理。
刘雪梅(1975-),女,统计师,主要研究方向:统计分析与应用等。

