基于小波包分解与局部均值分解排列熵的自适应轴承故障诊断*
□王名月□缪炳荣□袁成标
西南交通大学牵引动力国家重点实验室成都610031
基于小波包分解与局部均值分解排列熵的自适应轴承故障诊断*
□王名月□缪炳荣□袁成标
西南交通大学牵引动力国家重点实验室成都610031
轴承运行过程是一个复杂的非平稳动态过程,提出小波包分解与局部均值分解排列熵相结合的特征提取方法,以支持向量机为故障模式识别器,对轴承故障进行诊断。首先对原始振动信号进行小波包阈值消噪处理,根据特征频率进行频带划分及信号重构;然后采用局部均值分解方法将重构信号自适应分解为若干模态分量,并计算包含主要故障信息分量的排列熵,实现对模态分量的特征量化;最后将熵值特征向量输入多分类支持向量机,用于判断轴承的故障类型及故障程度。分析结果表明,这一方法的轴承故障诊断识别率可达95%,与其它方法相比,这一方法能够有效提取轴承故障特征,具有更高的识别准确率。
轴承;小波包分解;局部均值分解;排列熵;故障
轴承损伤性冲击故障早期表现出典型的非平稳性、调制性和微弱性特征,基于振动加速度传感器采集的轴承振动信号中包含大量的冲击和噪声,因此,从含噪声振动信号中提取故障特征是轴承故障诊断的关键[1]。对于轴承故障非平稳时变信号而言,传统的时域和频域方法都有各自的局限性。
局部均值分解(LMD)方法是一种新的非平稳信号自适应分解方法,由于其自适应性的时频分析特性,目前已广泛应用于复杂多分量的非线性、非平稳信号分析中。Ma Jun等[2]提出了一种基于LMD和包络解调的滚动轴承故障特征提取方法。TianYe等[3]将排列熵和LMD方法相结合,并将其应用于轴承故障诊断中。程军圣等[4]针对滚动轴承故障振动信号的非平稳特性,提出了一种基于LMD和神经网络的滚动轴承诊断方法。颜天晓等[5]提出了基于总体平均经验模态分解和希尔伯特变换包络分析的轴承复合故障诊断方法。杨斌、程军圣[6]对激励未知情况下的结构损伤模式进行识别,提出了基于小波包分解(WPD)、LMD和排列熵的结构损伤检测方法。
近年来,基于熵概念的信号分析方法已从医学、生物学、图像处理等领域应用到机械故障诊断,如近似熵、样本熵、模糊熵等。排列熵算法是一种新的动力学突变检测算法,能够反映出一维时间序列不规则程度和数据的微小变化。冯辅周等[7]将排列熵分别与小波相关滤波法、隐马尔可夫模型等结合,提出了小波相关排列熵,在齿轮、轴承等机械故障诊断中得到验证。郑近德、程军圣等[8]提出了基于局部特征尺度分解和排列熵的滚动轴承故障诊断方法。程军圣等[9]还将基于变量预测模型的模式识别方法与排列熵方法相结合,应用于滚动轴承故障诊断。周涛涛等[10]基于排列熵和连续隐马尔可夫模型,提出了齿轮故障诊断方法。
原始振动信号中存在大量的噪声,若直接对振动信号进行LMD,振动过程中的噪声信号将与故障信号相混淆,并共同参与分解,导致算法的边界效应加重,分解层数增加,使算法不易收敛,进而失去故障信号提取的意义[11]。笔者将WPD与LMD相结合,采用LMD算法对重构的故障信号子频带进行分解,得到若干模态分量,然后计算每种状态下分量的排列熵,最后采用适合小样本分类的支持向量机(SVM)进行故障诊断,结果表明这是一种有效的轴承故障诊断方法。
1 理论背景
1.1 WPD
试验分析数据往往存在噪声干扰,传统的信号降噪方法只适用于对平稳信号进行处理,而不适用于非平稳信号,因为这些方法等价于使信号通过一个低通或带通滤波器,在滤波平滑过程中滤掉了信号细节中的有用特征[12-13]。小波变换作为一种新的时频分析方法,已广泛应用于工程实际中。
WPD计算方法为:
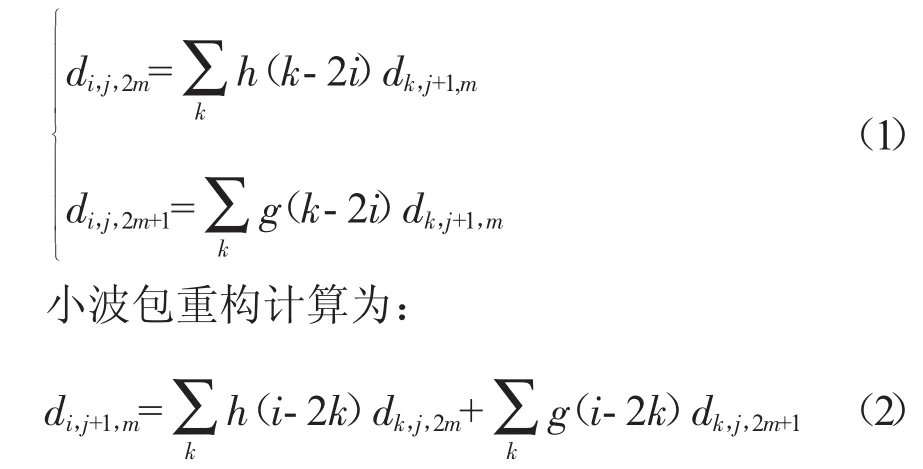
式中:di,j+1,m为j层m节点的第i个小波包系数;h(k)和g(k)为展开系数。
1.2 LMD
LMD的本质是从原始信号中分离出纯调频信号和包络信号,且每个包络信号与每个调频信号相乘可以得到的一个模态分量。对于任意给定的信号x(t),LMD过程如下:
(1)找出信号x(t)的所有局部极值点ni,计算出所有相邻的局部极值点的平均值[14]:

将所有相邻的平均值点mi用直线连接,然后用滑动平均法进行平滑处理,可以得到局部均值函数m11(t)。
(2)通过局部极值点ni求出包络估计值:

将所有相邻两个包络估计值用直线连接,然后用滑动平均法进行处理,得到包络估计函数a11(t)。
(3)从原始信号x(t)中将局部均值函数m11(t)分离出来,得到:

(4)解调h11(t),得到纯调频信号s11(t),并且重复上述过程直到调频信号s1n(t)的局域包络函数a1(n+1)(t)=1为止。

(5)模态分量的包络信号是迭代过程中所有局域包络函数的乘积:
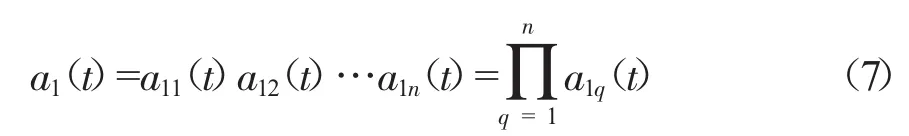
(6)模态分量α1(t)为包络信号a1(t)与纯调频信号s1n(t)的乘积,即:

(7)从原始信号x(t)中将α1(t)分离出后,得到剩余信号u1(t),重复以上过程k次,直到uk(t)为单调函数:

则原始信号最终表示为k个模态分量和一个单调函数uk(t):

1.3 排列熵特征提取
排列熵不仅计算简单、快速,抗干扰能力强,而且对信号数据的微小变化也比较敏感,其熵值γ的变化可以反映并放大系统动力学性能的变化,所以广泛适用于各种时间序列。
(1)假设由系统方程迭代得到的离散时间序列X={x(i)=1,2,…,n},其中x(i)为时间序列的第i个元素,n为元素的个数。按照塔肯斯定理对X进行重构,可得到矩阵[15]X:

式中:j=1,2,…,K;m为嵌入维数;τ为延迟时间;K为重构向量个数,K=n-(m-1)τ。
(2)对重构矩阵中每行分量的各元素进行升序重排列,即:
x[j+(q1-1)τ]≤x[j+(q2-1]τ≤…≤x[j+(qm-1)τ](12)式中:q1,q2,…,qm为重构分量中各个元素所在列的索引。
若重构分量中元素值相等,如x[j+(q1-1)τ]=x [(j+(q2-1)τ],则按照q1、q2的大小径向排序。如果q1<q2,则认为x[j+(q1-1)τ]≤x[j+(q2-1)τ]。
(3)对行分量中的各元素进行升序重排,可得到一组符号序列:

(4)向量重构时要满足K=m!,共有m!种,计算S(j)出现的概率Pj。
(5)按照香农熵形式,将时间序列X的排列熵Hp(m)定义为:

(6)当Pj=1/m!时,排列熵Hp(m)取得了最大值ln(m!),通常用ln(m!)对Hp(m)进行归一化处理,即:

式(15)中0≤Hp≤1,Hp的变化能将一维时间序列的微小变化放大,反映时间序列的随机程度,Hp越小,说明时间序列越规则,反之,说明时间序列越随机。
2 基于WPD与LMD排列熵的故障诊断
轴承故障早期,故障特征频率的能量比较微弱,不易提取,容易淹没在噪声中。为消除随机噪声和局部强干扰对特征提取的影响,提取有效的故障指标,采用基于WPD与LMD排列熵的滚动轴承故障诊断流程,如图1所示。

图1 故障诊断流程图
(1)采用小波阈值方法对原始信号进行消噪,并对消噪后的信号进行频谱分析。
(2)根据轴承故障特征频率及信号能量集中段,确定小波基及分解层数,对消噪信号进行N层WPD,保留特征频带进行小波包信号重构。
(3)对重构故障信号进行LMD,得到若干模态分量。
(4)选择前5个分量作为研究对象,并计算其排列熵,将其作为故障识别的特征向量T=[γ1,γ2,γ3,γ4,γ5]。
(5)将提取的排列熵特征向量输入SVM分类器进行训练,将测试样本输入训练好的SVM,从而确定轴承的故障类型及故障程度。
3 应用算例
采用美国凯斯西储大学的SKF 6205-2RS型深沟球滚动轴承实测振动数据,加速度传感器安装在电机驱动端,损伤状况为单一局部缺陷。电机转速为1 797 r/min,故障深度为0.177 8 mm,采样频率为12 kHz,分别采集轴承4种状态下的振动信号:正常状态、内圈磨损、外圈磨损及滚动体磨损,每种状态取40组数据样本,每个样本长度为2 048。
3.1 故障信号特征提取
LMD方法对噪声比较敏感,为消除噪声对诊断结果的影响,首先对原始信号进行小波包阈值消噪处理,得到加速度信号的时域波形,如图2所示。时域波形出现明显冲击,但波形较复杂,仅通过时域波形不易分辨轴承的工作状况。图3分别呈现了轴承内外圈磨损时的信号频谱,可以看出内外圈磨损振动信号的能量分别主要集中在0~1.5 kHz、2.5~3.5 kHz,表明故障信号的频率特征主要位于以上频段。

图2 消噪后故障信号时域波形

图3 轴承内外圈磨损信号频谱图及信号
对重构后的故障信号进行LMD,得到具有一定特征值的若干模态分量,如图4所示为外圈磨损信号的LMD分解。分解后的模态分量突出了数据的局部特征。为避免排列熵特征向量的样本数据冗长,同时简化分类器结构,计算前5个包含主要故障信息分量的排列熵。

图4 外圈磨损信号LMD结果
排列熵计算中有两个主要参数:嵌入维数m和延迟时间τ,其中嵌入维数m一般取3~7。若m过小,则算法失去有效性,不能检测序列的动力学突变;若m过大,不仅无法反映序列的细微变化,而且计算工作量较大[8,16]。文献[17]给出了确定τ和m的互信息法及假近邻法,延迟时间对时间序列的计算影响较小,这里取m=6,τ=1。
为验证笔者提出的WPD-LMD排列熵方法的有效性,分别将轴承故障信号直接进行LMD及经验模态分解(EMD),对比故障识别效果,各故障典型特征向量见表1。可以看出,4种工况各分量排列熵的统计特征明显不同,轴承正常状态时,振动信号各分量的排列熵值最大,这是因为信号的随机性和不确定性最大。轴承外圈相对固定,故熵值较小。滚动体运动较不规则,其熵值比内圈磨损和外圈磨损稍大。当然,并不能直接通过熵值判断轴承故障的位置。

表1 不同特征提取方法的典型特征向量
图5为故障信号基于LMD、EMD及WPD-LMD方法的第一个分量排列熵包络分布,可以看出EMD的端点效应最明显,其包络线存在严重摆动。图6为基于WPD-LMD方法提取的前3个模态分量的排列熵,即γ1、γ2、γ3,构成三维特征向量集。由图6可以看出,WPD-LMD提取的熵值在三维空间中不存在混叠现象,呈现了良好的类内聚集性和类间分离性,证明了基于WPD-LMD的故障特征提取方法的优越性和有效性。
3.2 基于SVM的轴承故障诊断
SVM精度高、泛化性好,克服了过拟合、局部最优解和收敛速度较慢等问题,能有效解决高维数、小样本情况下的模式分类问题。核函数对SVM非线性映射能力非常重要,选取核参数σ=3.4,惩罚参数C=2.25。对轴承4种工作状态各选取40组样本组成样本集,随机选取每种状态的20组特征向量对SVM进行训练,用于轴承工作状态的分类,其余的20组数据作为测试样本,进行模型有效性测试,见表2。
采用SVM对轴承4种特征进行分类,表3为3种方法的识别结果,由此可知,对于相同有限数量的样本,基于WPD-LMD排列熵的轴承故障识别率明显高于直接对故障信号进行LMD或EMD获取特征向量的方法,经小波包消噪和故障子频带重构后,故障信号LMD排列熵的SVM识别效果更好。WPD-LMD排列熵的轴承工作状态平均识别率为95%,图7为分类结果,其中正常状态、内圈磨损、外圈磨损及滚动体磨损的识别率分别为90%、95%、100%及95%。为进一步验证笔者所提方法的有效性,对轴承内圈的不同损伤程度也进行了分类。损伤深度分别为0.177 8 mm、0.355 6 mm、0.533 4 mm、0.711 2 mm,按照相同的分析步骤,获得熵值特征向量,建立SVM进行分类,分类结果如图8所示,平均识别率为92.5%,说明这一方法能够有效识别出轴承中不同位置、不同损伤程度的故障,提高了诊断精度和识别能力。
4 结论
针对轴承振动信号的非线性特征及噪声的干扰,为准确提取轴承故障冲击特征,笔者将WPD与LMD排列熵相结合,并以SVM作为分类器识别故障类型。
(1)小波包分析方法不仅能够有效地去除噪声,而且能够提取出包含故障信息的子频带,提高了后续LMD的精度,使故障特征的提取更加充分和准确,克服了传统方法的局限性,能够有效地提取轴承故障特征。
(2)排列熵可检测信号的随机性和动力学突变行为,相同故障状态下振动信号的LMD排列熵呈现γ1>γ2>γ3>γ4>γ5,与LMD后的波形变化一致,且滚动体熵值最大,内圈次之,外圈最小,排列熵能够更好地与机械故障信号进行匹配,从而体现机械故障特征。
(3)基于WPD-LMD排列熵的故障特征提取方法优于直接对信号进行LMD或EMD,将其与SVM结合应用到轴承故障识别,试验结果表明该方法具有可行性,实现了轴承状态和故障程度的有效分类,是一种有效的故障识别方法。

图53 种方法排列熵值分布情况

图6 WPD-LMD排列熵二维图

表2 轴承数据分类

图7 轴承不同工作状态分类结果

图8 轴承内圈不同损伤程度分类结果

表3 不同方法提取向量的故障位置识别结果
[1]李泽豪,顾海明,张亿雄.基于小波包和EMD的滚动轴承故障诊断[J].煤矿机械,2010,31(6):243-245.
[2]MA J,WU J D,FAN Y G,et al.The Rolling Bearing Fault Feature Extraction Based on the LMD and Envelope Demo dulation[J]Mathematical Problems in Engineering,2015,2015(6):1-13.
[3]TIAN Y,WANG Z L,LU C.Self-adaptive Bearing Fault DiagnosisBasedonPermutationEntropy andManifold-based Dynamic Time Warping[J/OL].http://doi.org/10. 1016/j.ymssp.2016.04.028.
[4]程军圣,史美丽,杨宇.基于LMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击,2010,29(8):141-144.
[5]颜天晓,张瑞亮,王铁,等,基于EEMD和Hilbert包络分析的轴承复合故障诊断研究[J].机械传动,2016(6):132-135.
[6]杨斌,程军圣.基于WPD-LMD和排列熵的结构损伤识别方法[J].湖南大学学报(自然科学版),2014,41(8): 41-46.
[7]冯辅周,饶国强,司爱威,等.排列熵算法研究及其在振动信号突变检测中的应用[J].振动工程学报,2012,25(2): 221-224.
[8]郑近德,程军圣,杨宇.基于LCD和排列熵的滚动轴承故障诊断[J].振动.测试与诊断,2014,34(5):802-806.
[9]程军圣,马兴伟,杨宇.基于排列熵和VPMCD的滚动轴承故障诊断方法[J].振动与冲击,2014,33(11):119-123.
[10]周涛涛,朱显明,彭伟才,等.基于CEEMD和排列熵的故障数据小波阈值降噪方法[J].振动与冲击,2015,34(23):207-211.
[11]孙伟,熊邦书,黄建萍,等.小波包降噪与LMD相结合的滚动轴承故障诊断方法[J].振动与冲击,2012,31(18): 153-156.
[12]杨文志,马文生,任学平.小波包降噪方法在滑动轴承故障诊断中的应用研究[J].噪声与振动控制,2009(4): 50-53.
[13]杨晨,阎树田,贺成柱,等.基于峭度与小波包络分析的滚动轴承故障诊断[J].机械制造,2014,52(2):62-64.
[14]WIDODO A,SHIMMC,CAESARENDRA W,et al.Intelligent Prognostics for Battery Health Monitoring Based on Sample Entropy[J].Expert Systems with Applications,2011,38(9):11763-11769.
[15]张晓涛,唐力伟,王平,等.基于排列熵的电磁声发射信号到达时间识别[J].现代制造工程,2015(5):126-130.
[16]郑近德,程军圣,杨宇.多尺度排列熵及其在滚动轴承故障诊断中的应用[J].中国机械工程,2013,24(19): 2641-2646.
[17]冯辅周,饶国强,张丽霞,等.基于EMD和排列熵的轴承异常检测方法研究[J].轴承,2013(2):53-56.
(编辑:小前)
上海电气“一带一路”最快援建项目成功冲转
日前,中国巴基斯坦经济走廊国家援巴一期重点工程、“一带一路”沿线启动最快的海外能源建设项目——巴基斯坦萨希瓦尔燃煤电站1号机组升速至3 000 r/min,一次冲转成功。
应巴政府的要求,该项目两台汽轮机、发电机的交货期仅12个月,创下了上海电气集团同类型机组的最快交货记录。萨希瓦尔燃煤电站全部投运后年发电量预计约90亿kWh,将极大缓解巴基斯坦严重缺电的局面,有效推动中巴经济走廊建设,进一步促进中巴两国战略合作伙伴关系。
此外,上海电气近期还将参与巴西、阿联酋电力项目。
Bearing run procedure is a complex non-stationary dynamic process.A feature extraction method combining WPD and LMD permutation entropy was proposed to diagnose the bearing fault when the SVM was used as fault mode recognizer.Firstly,the wavelet packet threshold de-noising was performed on the original vibration signal and the band division and signal reconstruction were carried out according to the characteristic frequency.Then the LMD method was adopted to decompose the reconstructed signal into several modal components,and the permutation entropy including the main fault information component was calculated torealize the feature quantization ofthe modal component.Finally,the feature vector of the entropyvalue was input intothe multi-classification SVMin order to estimate the fault type and fault degree of the bearing.The analytic results showthat this method can achieve 95%bearing fault recognition during diagnosis.Compared with other methods, this method can effectively extract the bearing fault signature with higher recognition accuracy.
Bearing;WPD;LMD;Permutation Entropy;Fault
TH165+.3
A
1672-0555(2017)02-001-07
*国家自然科学基金资助项目(编号:51375405)
2016年11月
王名月(1992—),女,硕士研究生,主要研究方向为结构损伤识别与故障诊断。

