互依变量分析在体育管理研究中的应用
Jerry J.Wang,Kevin K.Byon,James J.Zhang,安俊英
(1.美国西佐治亚大学体育管理、健康与教育系,佐治亚州卡罗顿30116;2.美国印第安纳大学运动学系,印第安纳州伯明顿47405; 3.美国佐治亚大学国际体育管理研究中心,佐治亚州雅典30602;4.上海体育学院经济管理学院,上海200438)
互依变量分析在体育管理研究中的应用
Jerry J.Wang1,Kevin K.Byon2,James J.Zhang3,安俊英4
(1.美国西佐治亚大学体育管理、健康与教育系,佐治亚州卡罗顿30116;2.美国印第安纳大学运动学系,印第安纳州伯明顿47405; 3.美国佐治亚大学国际体育管理研究中心,佐治亚州雅典30602;4.上海体育学院经济管理学院,上海200438)
介绍互依变量分析的统计程序与技术及其在体育管理研究中的应用,包括聚类分析、探索性因子分析、验证性因子分析,并结合实证研究的设计逐步进行说明,为体育管理研究者提供“即学即用”的研究方法指南。
体育管理;类别分析;因子效度;建构效度;互依变量分析;聚类分析;探索性因子分析;验证性因子分析
Author’s address1.Department of Sport Management,Wellness and Physical Education,University of West Georgia,Carrollton 30116,Georgia,USA;2.Department of Kinesiology,Indiana University, Bloomington 47405, Indiana, USA; 3.International Sports Management Research Center,University of Georgia,Athens 30602,Georgia,USA;4.School of Economy&Management, Shanghai University of Sport, Shanghai 200438,China
在相依变量分析中,研究者需要对因变量/效标变量(DV)和自变量/预测变量(IV)进行区分,而本文介绍的互依变量分析并不区分DV和IV[1]。互依变量分析的主要目的是探索一组变量间的潜在结构,而不是利用一个或多个IV对DV进行解释和预测。通常体育管理研究中的互依变量分析包括2种主要类型:Q分析和R分析[1-2]。Q分析旨在根据观测对象某些特征的相似性形成结构或分组,如聚类分析;R分析则根据一组变量的变量间相关系数生成结构或分组,如探索性因子分析(exploratory factor analysis,EFA)和验证性因子分析(confirmatory factor analysis,CFA)。
1 聚类分析
聚类分析被广泛应用于消费者市场细分研究,对消费者按照背景、心理、行为和(或)生活方式的同质性特征进行分组,算法保证每个聚类具有很高的内部同质性和外部异质性(不同聚类间)[3]。在聚类分析中,同质性和异质性通常是以距离进行评价,这有别于传统的因子分析,因子分析的评价标准是模式的相似性和变异性(即相关性水平)。在选择生成聚类的数量上,如果越多的聚类生成,聚类内部的同质性就会越大,聚类间的异质性也相应增大,然而这也会导致更复杂的模型。因此,研究者需要依据课题的具体情况平衡聚类的同质性和模型的复杂度。聚类的最佳数量需要根据统计结果的稳健性、概念原理以及研究的实用价值进行综合判断。
总体而言,聚类技术和过程包含2种通用的数学算法:分层聚类算法[4]和划分(分离)聚类算法[5]。对于分层聚类算法,算法运行之前研究人员并不知道有多少聚类会从收集到的数据中产生,因此有时识别聚类的数量也是研究的目的之一。为了实现这一目标,研究者必须具备很强的概念和理论水平,而不仅仅依赖大样本数据算法分析的结果。具体的算法是,首先测量观测对象在某些变量上的相似性,最常见的相似性测量是每一对观测对象之间的欧氏距离,即2个数据点之间的直线距离的测量[3],越小的欧氏距离代表越高的相似性。生成聚类时需要每次合并最近距离的2个观测对象或对象聚类,并重复进行以形成不同的分层,直至完成最后2个聚类的合并。分层过程可以利用一些主流的统计软件,如SPSS、SAS等自动完成,形成具体的分层结果和聚类方案。同时,数据分析所产生的树状图可更直接地显示每个聚类及相关距离。在水平型(垂直型)树状图中,纵(横)轴代表了具体的观测对象,横(纵)轴代表聚集系数。
对于划分聚类算法,研究人员在数据分析前已确定了生成聚类的数量。K-means聚类是这一类算法的代表,具体的算法是,研究人员首先根据相关文献和研究背景确定生成聚类的数量K,然后以每个聚类中所有观测对象的均值作为质心进行聚类运算(初始时,可任选K个观测对象作为质心)。在每一轮聚类运算中,计算出每个观测对象对K个质心的欧氏距离系数,并根据最小距离重新对观测对象进行划分,不断重复这一过程直至聚类模型收敛为止。K-means聚类算法快速简单,更适合于处理大样本的数据集。为了克服K-means聚类的缺点(如聚类数量K必须提前给定),研究人员需要依据相关理论确定K的取值。并且,当同时存在多个解决方案时,建议基于解决方案多次运行 K-means聚类算法以得到一个最优的聚类模型。
实证举例:在文献[6]中对体育彩票消费的研究中,研究者试图依据体育彩票消费者的消费模式和人口统计信息对其进行类型划分[6]。此项研究的基本问题是从数据中发现彩民的类型是否真实存在并获得彩民的聚类,而不是确定变量的结构,因此聚类分析被认为是最合适的研究方法。通过开展面对面的封闭式访谈,4 980名合格的受试者参加了该调查。他们在过去的12个月中至少购买过体育彩票1次。受试者被要求回答24项与体育博彩消费行为相关的问题,所有问题采用李克特5级量表编制,问卷同时测量受试者在体育彩票上的花费水平,并对每个受试者的人口统计信息进行收集。研究中对体育彩民的类型划分基于现有的测量模型,参照文献[7]中对“问题型博彩行为量表”的研究,研究人员在聚类分析之前对可能产生的聚类数量已有了大致的判断[7]。具体而言,有3个潜在的聚类解决方案:3-聚类、4-聚类以及5-聚类。因此,应用K-means聚类算法实际的分析过程是执行SAS软件中的PROC FASCLUS程序。统计结果显示,5-聚类的解决方案是最合适的类型划分模型。5-聚类解决方案的结果如表1所示。
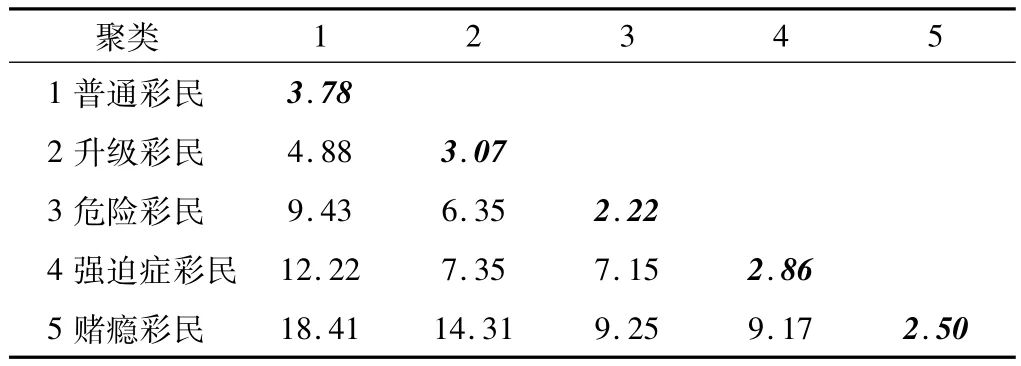
表1 聚类分析-5聚类方案的组内和组间变异Table 1 Cluster analysis-between and within group variability of a five-cluster solution
如前所述,一个较小的欧氏距离代表更高的相似性。在表1中,每个观测对象与其聚类质心之间的欧氏距离(即组内变异)小于聚类质心之间的欧氏距离(即聚类间变异性),代表了所提取的5个聚类的统计学差别。非常重要的是,研究人员也同时从理论上评估K-means聚类形成的5-聚类方案的合理性。在证实了5-聚类模型的理论合理性之后,研究人员基于每个聚类的人口统计信息和彩票消费特征进行命名。这5个聚类分别命名为普通彩民、升级彩民、危险彩民、强迫症彩民和赌瘾彩民。作为聚类分析的结果,建立一个体育彩民的类型划分,为相关的营利和非营利组织制定干预计划提供诊断参考。
2 探索性因子分析(EFA)
EFA是体育管理研究中使用最多的一种多元统计方法。EFA的主要目的:①确定一组变量背后潜在的因子结构和数量;②通过将高度相关的变量集聚在一起精简数据。其对一组变量中相关性较强的变量进行归纳,生成一个简约并具有代表性的变量结构。这种变量结构可以用来代表理论中的抽象的概念(latent construct),即该概念无法被直接测量,而只能间接地对相关的可观测变量进行评估。使用这种方法一般要求变量是连续变量,在一些特殊的估计中,EFA也可以处理类别变量[8]。EFA的分析步骤如下:
(1)评估样本大小。虽然对于样本的大小没有严格的规定,经验规则是样本容量与变量数量的比例最低达到5∶1,达到10∶1以上是比较理想的[1]。
(2)检验概念假设和统计假设的适当性。概念假设是指反映变量间潜在结构的理论原理,而统计假设是指变量间是否统计相关,相关性评估的标准有2个:①巴特莱特球形检验(BTS)是一种检验各个变量之间相关性程度的方法。它利用变量的相关系数矩阵判断变量是否适合用于做因子分析。统计上显著的BTS意味着变量的相关系数矩阵不是相同的,揭示了这些变量之间存在相关性。② Kaiser-Meyer-Olkin (KMO)检验是一种反映变量间整体相关程度的统计指数,旨在检查样本容量是否适合进行因子分析。一般而言,KMO的度量标准是:0.9以上表示非常适合; 0.8表示适合;0.7表示一般;0.6表示不太适合;0.5以下表示极不适合[1]。
(3)选择因子提取方法。考虑到因子分析是建立在所有变量之间的相关系数矩阵上,研究人员需要计算出一个变量的方差中与其他变量共享的部分(即公共方差,可以通过公因子方差衡量)、不能被共享的部分(即独特方差)以及测量误差造成的部分(即误差方差)。对于高度相关的变量,变量之间的公共方差(或公因子方差)相应较高,同时独特方差相应较低。在EFA中,研究者感兴趣的是变量之间的公共方差,并试图根据公共方差确定这些变量代表的潜在维度。此外,还存在另一种因子分析方法称为主成分分析法(PCA),其目的是用少数几个主成分从数据中抽取最大的总方差。虽然2种因子分析方法有类似的操作程序,但具体采用哪种分析方法应根据研究的目的进行合理选择。如果已知变量的独特方差和误差方差相对总方差很小,采用PCA;相反,如果公共方差、独特方差和误差方差均未知,采用EFA则比较合适[1]。
(4)提取因子数量的标准。预先确定的因子数量应与研究目标和概念合理性相适应。采取3种通用的统计标准确定保留的因子数量:①Kaiser规则,保留特征值等于或大于1.0的因子;②所保留的因子至少能解释所有变量60%的方差[1];③碎石图提供了因子数目和特征值的大小(图1)。

图1 探索性因子分析碎石图Figure 1. Screen plot in exploratory factor analysis
(5)因子旋转。将因子的参考轴旋转到某一位置,以减少含义不清的初始因子,并生成一个结构更简单、更易解释和理论上更有意义的因子解决方案。正交旋转和斜交旋转这2种旋转方法被广泛应用于体育管理研究中。对于正交旋转,旋转过程中轴必须保持90°正交,这种类型的主要方法包括:最大方差法(Varimax),它简化了因子矩阵的列;四次方最大值法(Quartimax),它简化了因子矩阵的行;相等最大值法(Equimax),它同时简化了因子矩阵的行和列。对于斜交旋转,旋转轴可以处于小于90°的理想位置。一些常见的斜交旋转方法包括直接斜交法(Oblimin)、Geomin法和最优转轴法(Promax)。Promax旋转同时结合了最大方差法(正交)和斜交旋转的技术[9]。在选择合适的旋转方法上,研究人员需要综合考虑具体的理论框架、数据特点和相关文献的研究结果[10]。
(6)决定保留的题项(变量)。有3种规则适用于这一过程:因子载荷的统计显著性、交叉或双因子载荷以及因子包含的最优题项数。对于因子载荷,样本容量很大时可以相应地降低对因子载荷的要求。为保证因子载荷的显著性,不同的因子载荷水平下样本大小的最低要求如下:① 0.30最低样本容量 350;②0.35最低样本容量250;③ 0.40最低样本容量200;④0.45最低样本容量150;⑤0.50最低样本容量120。对于交叉因子载荷,不保留具有交叉因子载荷的题项。在此交叉因子载荷是指一个题项同时在2个或以上的因子上具有中度到高度的载荷。对于因子包含的最优题项数,每个因子中至少保留3个题项是合适的[1]。从EFA中得到的因子应作为CFA的前导研究,并作进一步分析,CFA是一种理论驱动的因子处理方法[11]。
实证举例:文献[12]中检验了球迷对专业团队运动核心质量的感知(即比赛水平),它被概念化为对体育赛事核心特征的市场需求[12]。为了准确地理解球迷对专业团队运动的市场感知需求,研究者开发了评估专业团队运动核心特征的市场需求量表(Scale of Market Demand,SMD)。①通过广泛的文献回顾、田野调查以及针对专业队营销经理的访谈,确定市场需求的指标体系。SMD包含的所有题项综合考虑了专业团队运动独特的产品和服务特性。由此,SMD的初始版本中共有46个题项,包含主队、客队、运动特征、观赛成本、比赛促销、方便安排等子维度。② 所有题项采用李克特5级量表编制,通常在心理测量中李克特5级量表被视为连续变量。通过在不同的体育赛事现场调查和社区拦截填写问卷等方式收集数据,回收453份有效问卷用于数据分析,它们被随机分成两半,其中一半进行探索性因子分析。样本量略微超过5∶1的比例(即样本量与测量指标的比例)。
使用选定的数据集,利用EFA从SMD的题项中获得一个简单的结构[13],EFA采用最优转轴法Promax进行α因子提取[14]。EFA分析的主要目的是识别市场需求概念的潜在结构,实现从样本变量到通俗变量(被命名)的概念一般化,同时也可以把大量的题项减少至一个小得多的、易处理的因子集合。利用以下4个标准确定因子和其包含的题项:①因子特征值等于或大于1.0[15];②题项因子载荷等于或大于0.4,且不存在双重载荷[16];③一个因子至少包含3个题项[1];④因子和题项的保留必须有理论依据。此外,碎石图也被用于帮助决定提取因子的数量[17]。
分析结果如下:样本充足率指标KMO的取值为0.845,大于阈值0.70,表明公共方差的水平良好,该样本量适合进行因子分析[15]。巴特莱特球形检验BTS为4 521.27(P<0.001),变量的方差和协方差矩阵是一个单位矩阵的假设被拒绝,因此因子分析被认为是适当的。通过EFA,从31个题项中提取了6个因子,能解释变量57.69%的方差。从生成的碎石图看,也支持6因子模型的结果。根据预先设定的标准,题项的因子载荷小于0.4的9个题项被淘汰(它们是高水平表现、主队的明星球员、支持主队、高水平的技能、天气条件、势均力敌、客队的对抗、比赛激烈程度和座位的优势)。
另外,6个题项被移除,因为只有1个或2个题项被加载到相应的因子(它们是主队破纪录的表现、团队竞技、最好的球员在场上、球馆的位置、热爱专业团队运动、专业团队运动的流行程度)。最后,包括31个题项的6个因子被命名为:客队(9题项)、主队(6题项)、比赛促销(5题项)、观赛成本(4题项)、运动特征(4题项)、方便安排(3题项)。解析后的因子结构总体符合本文研究中SMD量表的概念模型。EFA保留的题项将用于后续的CFA,将在下一节中介绍。通过Promax旋转后得到的系数矩阵如表2所示。
3 验证性因子分析(CFA)
通过上面的EFA,得到了一个简单的因子结构,通常它被认为是一个初步的结果,因为仅仅从数据样本中提取因子使得测量模型缺乏理论基础。尽管在EFA中也利用理论选择题项或变量、确定潜在的因子和给因子提供理论解释,但因子仍在很大程度上取决于一个研究样本。通常情况下,一个EFA中得到的因子结构可以作为CFA的前导研究,CFA被认为是一种相对由理论驱动的验证方法[1]。故CFA已成为一种常规的应用于心理特征观测的统计方法。
若进行CFA需要以下5个步骤:(1)模型设定。

式中,p是模型中观测指标的数量。如果有4个观测指标,协方差矩阵会产生指标变量独特方差和协方差信息,即4个独特方差和6个协方差。
(3)模型估计。需要将独特方差和协方差的数量与模型需要估计的参数数量进行比较:如果前者小于后者,则被认为是不可识别的模型。即独特的方差和协方差的数量太少以至于不能估计模型;如果2个数字相等,那么该模型被称为恰好识别,因子模型的自由度为零,即只存在一个模型估计的结果;如果前者大于后者,那么因子模型被过度识别,模型估计的自由度大于零。前2种都不是模型估计的理想情况,研究人员需要努力构造一个过度识别的因子模型。如果一个模型只有一个潜在的因子,则潜因子至少有3个指标(每个指标均包含与指标相关的误差项)不相关才能保证模型是过度识别的。
除了识别问题,其他因子分析的一般规则也适用于CFA,比如不能有交叉载荷的指标以及一个因子至少有3个测量指标。因为CFA涉及潜在的因子,它不能观察到或直接测量,所以使用多个可观测指标捕捉潜在因子的方差。此外,增加更多的观测指标能增加因子过度识别的程度以及因子的可靠性,进一步提高测量模型的估计质量。在EFA中的建议样本容量也可用于确定CFA的样本大小。即至少应达到样本容量与指标数量的比例5∶1,并努力实现10∶1的比例。
(4)模型拟合优度检验。研究人员需要评估测试模型对数据集的拟合优度。以下是一些体育管理研究中在评估测量模型的拟合优度时被广泛采用的一般指数:
①正态卡方值(Normed Chi-square)。该指标是计算出一个卡方自由度比。鉴于卡方值随着样本容量的增加而膨胀,有必要计算一个加权的指数。即便如此,正态卡方值在样本容量很大时依然取值较大。一般而言,样本小于750个时,正态卡方值小于3.0表示模型具有好的拟合度[1,18]。基于理论构造模型的潜在因子结构和相关的观测指标。
(2)模型识别。检查模型是否可识别,即样本协方差矩阵是否提供了足够的信息形成一个测量模型。变量的独特方差和协方差的数量N可以通过以下公式计算:

表2 市场需求量表的因子系数矩阵Table 2 Factor pattern matrix for the scale of market demand variables
② RMSEA指数(Root Mean Square Error of Approximation)。RMSEA的取值表示模型在多大程度上符合总体,因此该指数对样本大小不敏感。RMSEA值越小表示模型拟合度越好。一般而言,RMSEA值小于0.6表示好,在0.6~0.8表示一般,大于0.8表示差[19-20]。
③CFI指数(Comparative Fit Index)。CFI用来评估拟建模型和零假设模型的适合度[21]。它的一个突出的优点是对因子模型的复杂度不敏感[1]。一般而言,CFI值大于0.90表示较好的拟合度[19]。
④SRMR指数(Standardized Root Mean Residual)。每个协方差的估计误差会产生残差。SRMR指数是平均标准化的残差。其值在0.0~1.0变化,值越小表示模型拟合度越好。一般而言,SRMR<0.08表示一个可接受模型拟合度水平[19]。
除了评估因子模型的拟合优度指标,构建测量模型的效度与信度也需要进一步检查。主要包括3种类型:聚合效度;区分效度;理论效度。聚合效度是指构成因子的多个指标共享方差的比例,它通常是由3个指标进行评估,包括标准化因子载荷、平均方差提取(AVE)和建构信度(CR)[1]。其中:① 标准化因子载荷代表一个指标的公因子方差。标准化因子载荷的平方就是能被该指标解释的因子方差的多少。理论上建议一个指标应解释50%或更多的一个因子的方差,即标准化因子载荷应大于0.70,至少达到0.50或更高。② 平均方差提取(AVE)是聚合效度的另一个重要指标,它表示一个指标的因子载荷提取因子方差的平均值[1]。根据这个定义,AVE的值可以通过下式计算:

一般来说,建议AVE的值达到0.50或更高。③建构信度CR是指标因子载荷的平方总和与指标总方差的平方之和的比例,可以用以下公式计算:
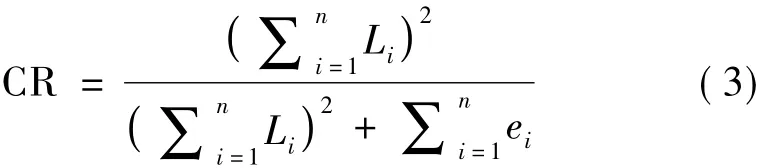
式中:Li是指标i的标准化因子载荷;ei是误差方差。一般来说,CR值在0.60~0.70表示一个可接受的水平,高于0.70表示较好的可靠性。
区分效度是指一个潜在因子在多大程度上与其他因子存在差异[22]。通常采用皮尔逊相关系数评估2个因子的区分效度。根据经验法则,因子间相关系数小于0.85表示一个可接受的区分效度水平[18]。更严格的评估区分效度是将AVE与潜在因子的平方相关进行比较。Fornell等[23]建议因子之间的平方相关必须低于任何一个因子的AVE值。理论效度是检验在多大程度上当前目标因子与其他相关理论形成的因子之间存在相关性[24]。显著的相关性将支持提出的测量模型的理论合理性,其评估既包括采用相关标准做概念内部的判断,也包括独立于测量概念的预见性标准。此外,克伦巴赫系数α常被用来评估提出的因子模型的信度,它表示一组指标在多大程度上存在相关性[25],可以通过下式计算:

其中,α介于0.0~1.0。克伦巴赫系数α越大表示模型信度越好。一般而言,克伦巴赫系数α的值应该达到0.70或更高[18]。
(5)模型修正。如果这些指数低于建议的标准,研究人员需要通过修正指数修改模型及其包含的因子和题项,修正指数则基于因子结构中未指定的相互关系计算,修正指数的计算程序通常包含在Mplus和AMOS等统计软件包中。需要注意的是,修改因子模型不仅基于实证方面(如因子载荷),也要以理论作为基础。CFA的具体操作步骤见实证研究案例。在实践中,当从数据中得到多个可能的因子结构方案时,需要进一步比较不同模型的拟合优度、效度和信度、理论的合理性以及遵从精简原则等进行选择。
实证举例:前面已经使用文献[12]的研究说明EFA的用法,这里继续用它说明CFA的使用程序。在此案例中,执行AMOS的CFA程序对前面EFA中保留的SMD因子进行最大似然估计(ML),将另一半数据集提交给 CFA程序,对一个包含31题项的6-因子测量模型进行ML估计,拟合优度指数显示6-因子测量模型对数据的拟合度不佳,正态卡方值(χ2/df=3.20)高于建议截止值(<3.0),表示拟合度差。RMSEA值也显示 6-因子模型拟合度差(RMSEA=0.10,90%CI=0.094-0.106)。虽然SRMR值(0.08)在可以接受的范围内(≤0.10),而CFI值(0.78)大大低于推荐截止值(>0.90),也表示模型对数据的拟合度不佳,拟合度检验的总体结果是建议修改或重新设定模型。文献[26]中也建议在模型对数据的拟合度不佳时,模型应该重新被设定[26]。在当前的分析中,指标载荷范围从0.398 (团体票成本)到0.903(广告)。在31个题项中,有9项指标载荷低于0.707,表明这些指标的误差方差大于它们的共享方差。因此,这9项指标(即客队历史传统、主队士气、网络信息、旅行距离、比赛观赏性、比赛速度、团体票成本、比赛持续时间、主队历史传统)被删除。此外,修正指数表明拟合度问题与其他5项指标(即客队明星球员、主队球员整体水平、客队联赛积分排名、宣传、客队球员的个人魅力)有关,这5个指标存在严重的双重因子载荷问题,双因子载荷系数的范围为0.50~0.60,表明单个指标不止在一个因子上负有载荷。通过仔细审视这些统计判断,最后决定把以上14个题项从模型中删除。
在对模型进行重新设定后,得到一个包含17个题项的5-因子模型:主队(3题)、客队(5题)、比赛促销(3题)、观赛成本(3题)、方便安排(3题)。利用CFA对新的5-因子模型进行分析。拟合优度指数显示5-因子模型对数据的拟合度非常好。正态卡方值(χ2/df=2.55)低于建议的截止值(<3.0),RMSEA值也表明5-因子模型的拟合度可以接受(RMSEA= 0.084,90%CI=0.072~0.096),SRMR(0.054)的值非常好(≤0.10),CFI(0.92)被认为是可以接受的。总体来看,5-因子模型的拟合优度大幅改善,表示该模型比6-因子模型有更好的可接受性(表3)。因此,选择5-因子模型作进一步的研究。
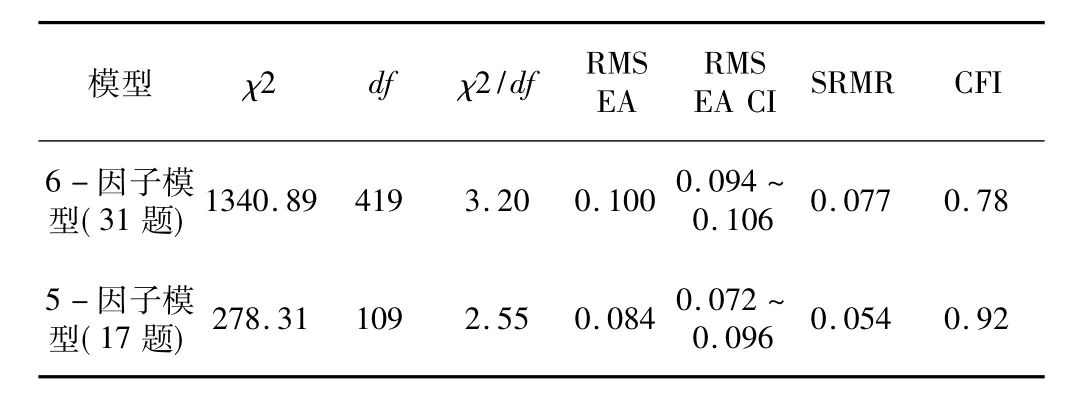
表3 6-因子模型和5-因子模型的拟合优度指标Table 3 Goodness-of-fit indexes of six-factor model and fivefactor model
接下来,对5-因子模型进行信度分析。5-因子模型的各个因子和题项的信度评估采用 CR(阈值0.70)和AVE(阈值0.50)进行。如表4所示,5个因子的CR值范围从0.76(观赛成本)到0.82(客队,比赛促销)。
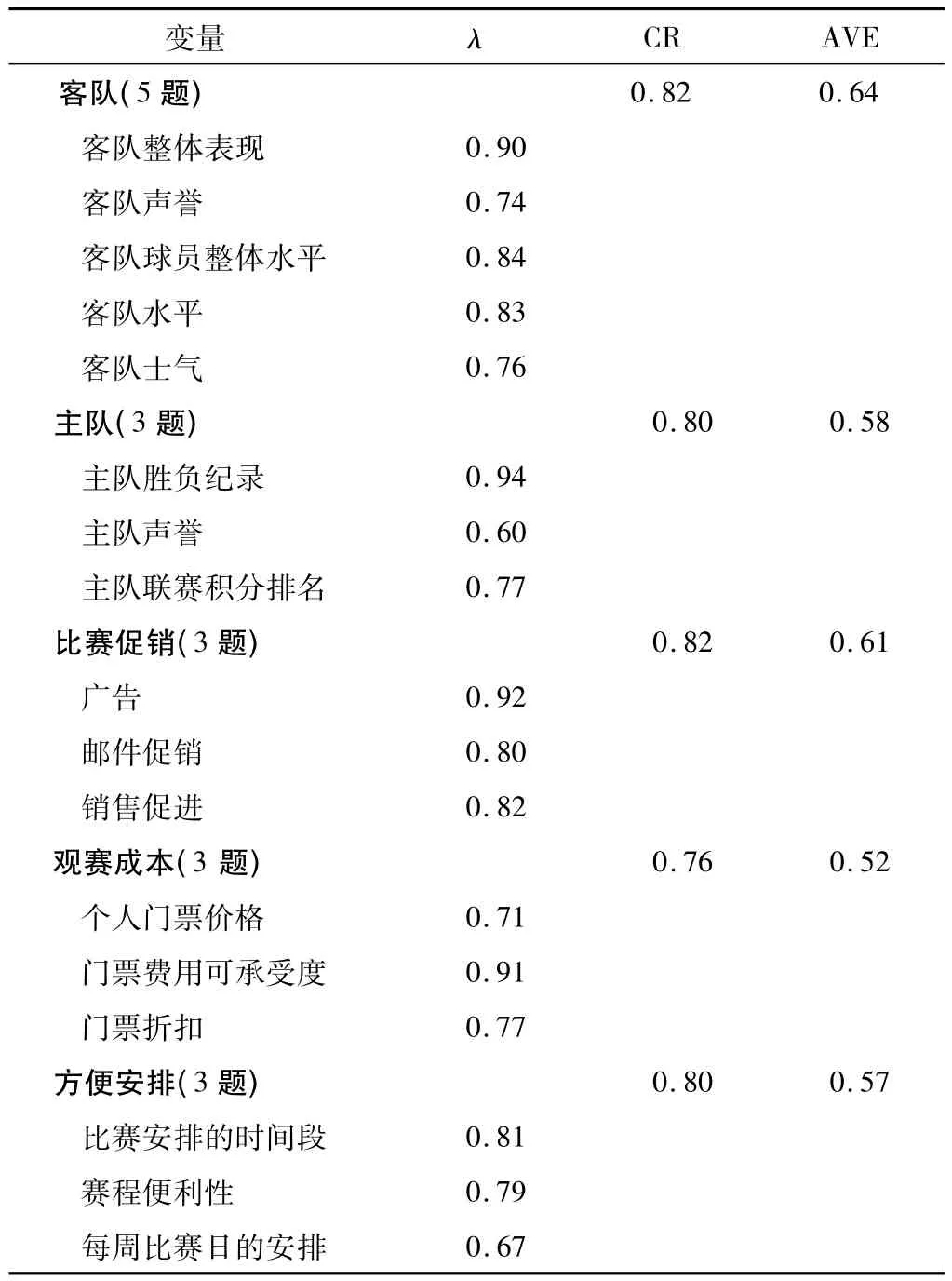
表4 5-因子模型的因子载荷(λ)、建构信度(CR)、平均方差提取(AVE)Table 4 Factor ladings(λ)、construct reliability(CR)、and average variance extracted(AVE)for the fivefactor model
此外,所有因子的AVE值高于建议的标准,从0.52 (观赛成本)到0.64(客队)。基于信度检验的整体信息,确定各个因子是可靠的。所有指标的载荷是统计显著的,z分数从8.99到16.79(P<0.05)。此外,除了主队声誉(0.60)和每周比赛日的安排(0.67)外,所有指标的载荷大于建议的标准0.707[27]。决定保留这2项的原因是其在理论上与主队和方便安排2个因子联系紧密,且取值上只略低于阈值0.707。总体而言,5-因子SMD模型具有一个简单紧凑的结构。
模型中不存在因子间相关系数大于0.85的情况,取值范围从0.19(比赛促销与观赛成本之间)到0.51 (观赛成本与方便安排之间),表明SMD因子具有可接受的区分效度。同时,Fornell等[23]的测试发现,所有因子的平方相关均低于每个因子的AVE值,说明模型具有很好的区分效度。总体而言,基于上述2个CFA的结果分析,包含17题项的5-因子模型被认为是最合适的测量专业团队运动的市场需求量表(SMD)。
4 讨论
相对EFA而言,尽管近年来学术论文中CFA的使用稳步增加,但学术界关于EFA和CFA使用的争论从未停止过。诚然,CFA似乎是一个更受欢迎的统计方法(鉴于CFA的理论驱动与EFA的数据驱动),因此得到研究人员的青睐,甚至是一些审稿人在背后“推波助澜”。然而,将CFA凌驾于EFA之上显然言过其实,EFA和CFA作为相互依存的分析工具各有其优点。关于“CFA和EFA之间哪种方法更好”的问题,答案是两者都很重要,使用则取决于具体的研究问题。EFA的主要目标是识别模型的潜在结构,而CFA的主要目标是验证假设模型的潜在结构。因此,不建议在没有适当理由的情况下,采用EFA测试先验的假设模型。
在此澄清一些在EFA和CFA使用中出现的疑问。在许多使用CFA进行模型构建和验证的研究中,模型的再指定往往是利用修正指数。首先,尽管CFA中包含了帮助研究者进行模型拟合度改进的程序(如修正指数和规范检索),但是一旦对原模型进行修正,这一过程将被认为不再是验证性而是探索性,因为模型的再指定改变了建立模型的初始假设[28]。当采用原始样本对修正模型进行估计时,“自我验证”(即直接把探索性因子分析的结果放到同一数据的验证性因子分析中)问题就会出现,因为这不是理论驱动的模型检验,而是数据驱动的模型构建。同时由于CFA被认为是比EFA更严格的模型测试方法,这样就比较难达到验证理论的目标了。此外,体育管理研究中数据收集的过程可能不是完全随机的,这就意味着样本不能真正代表总体,也会导致CFA分析的模型不被数据支持。因此,在利用指数进行模型修正时必须特别谨慎。由于有证据表明可能产生“自我验证”问题,采用独立样本对修正模型的估计结果与采用原始样本估计的结果会不一致[29]。建议的程序如下:① 建立先验的假设模型;②采用CFA对模型进行估计;③当模型不被支持时,优先考虑基于理论修改模型,然后才是利用修正指数修改模型(即理论和指数结合起来使用);④采用独立样本重新估计修正后的模型。
另一类体育管理文献中常见的错误是在CFA和EFA分析中采用同一个样本数据。由于“自我验证”问题的存在,这种做法是完全错误的。利用EFA,研究者可以得到关于数据的全部潜在结构,当然这个结构没有任何的理论基础。因此,在EFA得到的模型之上,利用同样的数据进行CFA只是一个数据驱动的模型估计而不是对先验模型的验证。如果一个EFA得到的模型被认为与理论相符,必须在CFA中采用新的数据集进行检验,以避免产生“自我验证”的问题[28]。建议的程序(特别是在大样本的情况下)是将数据分为两半,一半用于EFA,一半用于CFA[12]。另一个建议是当构建模型过程是基于理论时,首先用CFA进行模型检验,如果模型不被支持,再采用EFA找出模型的“差异”。在这种情况下,EFA和CFA可以采用同一个数据,因为其本质还是探索性的过程。如果研究者需要确认最终的因子结构,还是需要在CFA中采用独立的样本数据[30]。
EFA和聚类分析的相似性在实践中也会产生一些混淆。例如,2种方法都是探索性的和数据驱动的,目标都是探索数据集的潜在结构,并简化该数据集。2种方法的本质区别是聚类分析关注研究对象的结构,EFA关注对自变量的分析。此外,2种方法的类别评价标准也不同。聚类分析采用距离评价聚类的同质性,而EFA采用变异(即相关系数)生成因子。尽管EFA和聚类分析都是数据驱动的方法,对研究样本的选择也影响最后的因子或聚类的结构。因此,为了保证因子或聚类的效度和信度,研究者必须尽可能地选择具有代表性的样本和注重最终模型的理论合理性。值得一提的是,聚类分析不仅用于对人的聚类(例如,观众、参与者和运动员),同样也适用于其他的研究对象,如体育组织、地理区域和社区等。
本文对3种互依变量的统计分析方法进行了逐一说明。聚类分析通常用于市场营销或管理细分研究中,基于人口统计学、认知、情感、行为和生活方式等因素或变量对人群进行分类(如消费者、企业员工等)。探索性因子分析和验证性因子分析是从大量的直接观察指标中识别并确认因子结构和潜在变量的统计分析方法,是2种被广泛应用的研究方法。虽然理论上可以应用因子分析对一个包含多个概念的模型进行因子评估,然而,较好的实践准则是每次针对单一领域单一概念的一个或相关的多个因子进行因子分析,分析可能涉及认知、情感、动机或行为等领域。由于探索性因子分析和验证性因子分析是当前在体育管理研究中定量检验一个测量或量表的建构效度的先决条件,故本文也为如何在体育管理研究中开发具有良好效度和信度的测量奠定了基础。
[1] Hair J F,Black W,Babin B J,et al.Multivariate data analysis[M].Upper Saddle River,N J:Pearson Prentice Hall,2010:89-470
[2] Basilevsky A T.Statisticalfactor analysis and related methods:Theory and applications[M].Hoboken,N J: Wiley,2009:1-36
[3] Everitt B,Landau S,Leese M.Cluster analysis[M].London:Arnold,2001:10-89
[4] Jain A K,Murty M N,Flynn P J.Data clustering:A review[J].Acm Computing Surveys,1999,31(3):264-323
[5] Kaufman L,Rousseeuw P J.Finding groups in data:An introduction to cluster analysis[M].Hoboken,N J:Wiley,1990:37-49
[6] Li H,Mao L L,Zhang J J,et al.Classifying and profiling sports lottery gamblers:A cluster analysis approach[J].Social Behavior& Personality:An International Journal,2015,43(8):1299–1318
[7] Li H,Mao L L,Zhang J J,et al.Dimensions of problem gambling behavior associated with purchasing sports lottery[J].Journal of Gambling Studies,2012,28(1):47-68
[8] Gorsuch R.Factor Analysis[M].Hillsdale,N J:Erlbaum,1983:1-65
[9] Fabrigar L R,Wegener D T,MacCallum R C,et al.Evaluating the use ofexploratory factor analysis in psychological research[J].Psychological Methods,1999,4 (3):272-299
[10] Pett M A,Lackey N R,Sullivan J J.Making sense of factor analysis:The use offactoranalysisforinstrument development in health care research[M].Sage Publications,2003:85-164
[11] Gerbing D W,Hamilton J G.Viability of exploratory factor analysis as a precursor to confirmatory factor analysis[J].Structural Equation Modeling:A Multidisciplinary Journal,1996,3(1):62-72 [12] Byon K K,Zhang J J,Connaughton D P.Dimensions of general market demand associated with professional team sports:Development of a scale[J].Sport Management Review,2010,13(13):142-157
[13] Stevens J.Applied multivariate statistics for the social sciences[M].Mahwah,N J:Lawrence Erlbaum,1996:325-381
[14] Hendrickson A E,White P O.Promax:A quick method for rotation to oblique simple structure[J].British Journal of Mathematical and Statistical Psychology,1964,17(1):65-70
[15] Kaiser H F.An index of factorial simplicity[J].Psychometrika,1974,39(1):31-36
[16] Nunnally J C,Bernstein I H.Psychometric theory[M].New York:McGraw-Hill,1994:23-98
[17] Cattell R B.The scree test for the number of factors[J].Multivariate Behavioral Research,1966,1(2):245-276
[18] Kline R B.Principles and practice of structural equation modeling[M].New York:Guilford,2005:7-25
[19] Hu L T,Bentler P M.Cutoff criteria for fit indexes in covariance structure anaysis:Conventional criteria versus new alternatives[J].Structural Equation Modeling:A Multidisciplinary Journal,1999,6(1):1-55
[20] MacCallum R C,Browne M W,Sugawara H M.Power analysis and determination of sample size for covariance structure modeling[J].Psychological Methods,1996,1(2) (2):130-149
[21] Bentler P M.Comparative fit indexes in structural models[J].Psychological Bulletin,1990,107(2):238-246
[22] Campbell D T,Fiske D W.Convergent and discriminant validation by the multitrait-multimethod matrix[J].Psychological Bulletin,1959,56(2):81-105
[23] Fornell C,Larcker D.Evaluating structural equation models with unobservable variables and measurement error[J].Journal of Marketing Research,1981,18(1):39-50
[24] Churchill G A. Marketing research: Methodological foundations[M].Chicago,IL:Dryden,1995:51-121
[25] Cronbach L J.Coefficient alpha and the internal structure of tests[J].Psychometrika,1951,16(3):297-334
[26] Tabachnick B G,Fidell,L S.Using multivariate statistics[M].New York:Harper Collins,2001:628-675
[27] Anderson D R,Gerbing D W.Structural equation modeling in practice:A review and recommended two-step approach[J].Psychological Bulletin,1988,103(3):411-423
[28] MacCallum R C,RoznowskiM,NecowitzL B.Model modifications in covariance structure analysis:The problem of capitalization on chance[J].Psychological Bulletin,1992,111(3):490-504
[29] Williams L J. Covariance structure modeling in organizational research:Problems with the method versus applications of the method[J].Journal of Organizational Behavior,1995,16(3):225-233
[30] Braunstein J R,Zhang J J,Trail G T,et al.Dimensions of market demand associated with pre- season training: Development of a scale for major league baseball spring training[J].Sport Management Review,2005,8(3):271-296
Application of Interdependent Variable Analysis in Sport Management Research
Jerry J.Wang1,Kevin K.Byon2,James J.Zhang3,AN Junying4
The current article aims to introduce a comprehensive setof statisticalprocedures and techniques of conducting interdependence analysis in the context of sport management.As three majortypes,interdependenceanalysis,clusteranalysis,exploratory factor analysis,and confirmatory factor analysis are presented and discussed respectively,combined with the research design of empirical studies,as well as the step by step analytical instructions,which provides sport management researchers with the read-to-use guidance in research practice.
sport management; classification analysis;factor validity;constructvalidity; interdependentvariableanalysis; cluster analysis; exploratory factor analysis; confirmatory factor analysis
G80-05
A
1000-5498(2017)04-0041-08
2016-10-20;
2017-03-18
Jerry J.Wang(1986-),男,河南洛阳人,美国西佐治亚大学助理教授,博士;Tel.:(706)201-7183,E-mail:wangjq817 @gmail.com
安俊英(1980-),女,山西交城人,上海体育学院副教授,博士;Tel.:(021)51253275,E-mail:anjunying @sus.edu.cn
DOI10.16099/j.sus.2017.04.008

