基于广义似然比判决的混沌信号重构方法∗

任子良 秦勇 黄锦旺 赵智 冯久超

1)(华南理工大学电子与信息学院,广州 510641)

2)(东莞理工学院计算机与网络安全学院,东莞 523808)

基于广义似然比判决的混沌信号重构方法∗

任子良1)2)秦勇2)黄锦旺2)赵智1)冯久超1)†

1)(华南理工大学电子与信息学院,广州 510641)

2)(东莞理工学院计算机与网络安全学院,东莞 523808)

(2016年9月7日收到;2016年11月20日收到修改稿)

由于传感器网络的自身特征和节点的资源受限,使得对观测信号的处理必须考虑量化和能耗等因素,而引入的量化噪声同时增加了系统整体噪声的复杂性.针对传感器网络中整体噪声统计特性难以准确数学建模的特点,提出了一种基于代价参考粒子滤波的混沌信号重构算法.算法采用容积点变换以获得相对准确的更新粒子,并将局部重构信号的代价增量构建为广义似然比函数,用来选择传感器网络中的有效工作节点.仿真结果表明：所提算法可实现混沌信号的有效重构,且在噪声统计特性未知时性能要优于容积卡尔曼粒子滤波算法;算法同时能够通过选择不同的广义似然比阈值,实现网络能耗和重构精度的折中.

代价参考,混沌信号重构,能耗,广义似然比

1 引 言

传感器网络中通过节点间的相互协作,可以完成复杂的信号处理任务,已被广泛应用于生物医学、环境监测、工业控制等诸多领域[1-3].盲信号重构/提取是一种仅依靠传感器阵列中的部分观测数据实现对源信号重构/提取的信号处理技术[4-8].为了扩展盲信号处理技术的应用范围,可以将应用场景从传感器阵列扩展到传感器网络,但同时将受到网络节点带宽和拓扑结构等约束条件的制约[5,6,9-13].这些约束条件将直接导致信号处理方法的性能下降,而节点能耗更是影响整个网络生命周期的直接因素,因此研究适合传感器网络的盲信号处理方法具有重要的应用意义.

混沌信号具有的宽频带和不确定等特性,使其可被应用于无线加密和扩频等混沌通信系统[7].作为混沌通信中的基本技术手段,目前已有多种方法实现了信号的盲重构/分离,其中基于贝叶斯框架的非线性滤波是一类有效的实时处理方法[8-13].文献[8]和[9]分别采用无先导卡尔曼滤波方法(unscented Kalman filter,UKF)和容积卡尔曼滤波(cubature Kalman filter,CKF)实现了盲信号的重构和分离,文献[10]采用粒子滤波(particle filter,PF)实现了信号的盲提取,文献[11—13]进一步在传感器网络中实现了带宽或能耗约束下的混沌信号重构.在以上滤波算法的设计和实现过程中,均以系统噪声的先验统计特性已知为前提,而在传感器网络的实际应用中,很难对信号在观测、量化、传输等过程所引入的噪声进行精确的数学建模.针对非线性滤波算法的不足,文献[14,15]在PF的基础上提出了一种不依赖于噪声统计特性的代价参考粒子滤波算法(cost reference particle filter,CRPF).CRPF算法通过用户自定义代价函数和风险函数来实现粒子的重采样和传播更新,能够在噪声未知条件下实现非线性系统的状态估计[16-19].基于传感器网络的制约条件,本文提出了一种带宽和能耗约束下的代价参考容积卡尔曼粒子滤波算法(cost reference cubature particle filter,CRCPF)来解决噪声未知时混沌信号的重构问题.CRCPF算法采用容积点变换规则获取相对准确的重采样粒子,并通过构造局部重构信号的广义似然比来选择有效的工作节点,以降低网络的整体能耗.最后通过计算机仿真实验对算法性能进行评估,其结果验证了所提算法的有效性和健壮性,同时讨论了噪声统计特性已知/未知时算法重构性能和网络能耗的折中情况.

2 混沌信号重构模型

考虑传感器网络中利用N个节点对源混沌信号sk进行观测,设混沌信号的映射方程为

传感器节点的观测方程为

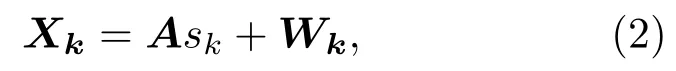
其中,k=1,2,···,K为离散时刻序列,Xk=[x1,k,x2,k,···,xN,k]T为k时刻观测列矢量信号,A=[a1,a2,···,aN]T为未知的时不变混合系统,Vk=[vk]和Wk=[w1,k,w2,k,···,wN,k]T为k时刻的系统过程噪声和观测噪声.忽略信道传输畸变影响,设量化过程引入的量化噪声为[q1,k,q2,k,···,qN,k]T,则系统的整体噪声可表示为Uk=[w1,k+q1,k,w2,k+q2,k,···,wN,k+qN,k]T,可得量化后的观测信号：

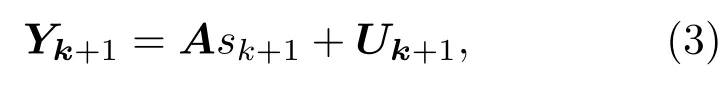
则(1)和(3)式构成了传感器网络中信号重构的状态观测方程.

另一方面,传感器网络的拓扑结构可分为无簇模型和有簇模型,无簇网络是有簇网络的特例,两种模型的信号重构方法一致.无簇网络中,节点各自将量化后的观测数据直接发送至数据融合中心进行重构.在有簇网络中,算法要进一步完成工作节点的选择,分为三个步骤：1)在各簇头上对收集到的量化观测信号进行容积点变换和代价参考滤波,得到局部重构信号;2)在各簇头上通过广义似然比判决选择有效的工作节点;3)将工作节点的广义似然比映射为噪声方差,在融合中心上利用最小二乘法(least square method,LSM)实现混沌信号的全局重构.

3 CRCPF信号重构方法

代价参考粒子滤波方法是一种基于蒙特卡罗方法的概率递推非线性滤波算法,定义k时刻的粒子代价函数C(·)和风险函数R(·)为

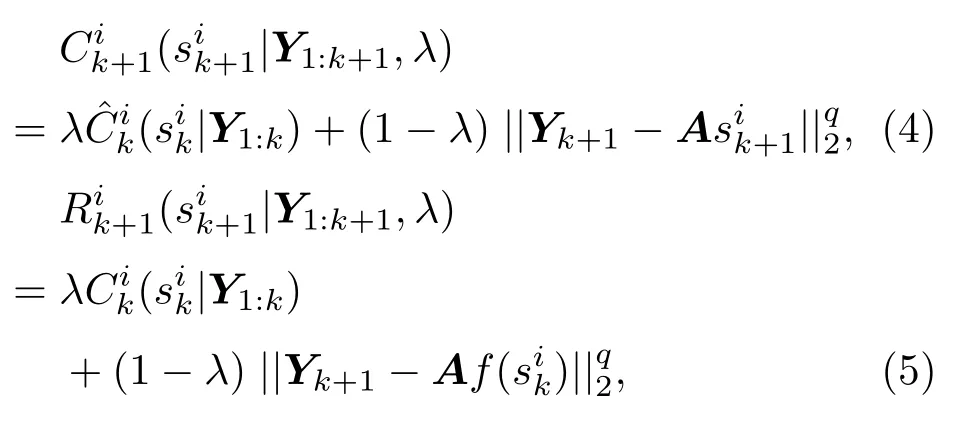
其中,λ∈(0,1)是遗忘因子,用来调节粒子前一时刻代价和风险值对当前值的影响,当λ=0时表示k时刻粒子代价值对k+1时刻无影响.表示2-范数的q次方,粒子代价增量由(4)式右边第二项引入.粒子重采样过程保留小代价样本粒子,丢弃大代价样本粒子.粒子代价值越小表示越接近粒子的真实状态,则粒子的更新传播权重越大.

此外,通过自定义单调递减函数µ(·),将粒子风险预测值和代价值映射为粒子的重采样概率和后验权重,其重采样概率为

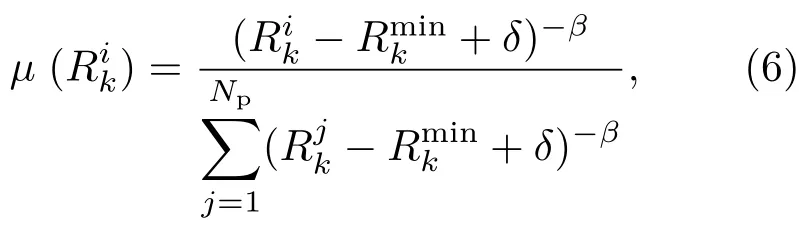
其中,Np表示粒子数量,δ∈(0,1)和β＞1分别为权值和范数调节系数.去掉项可保证映射后的重采样概率不会集中在个别权值较大的粒子上,从而保证了重采样后的粒子多样性.参数δ用来调节因粒子风险预测值过小或过大而引起的粒子权值误差,以保证映射的粒子权值更加准确有效.

3.1 构造广义似然比判决函数

在有簇网络模型的簇头节点上构造广义似然比函数的目的,是为了剔除一些对信号重构精度贡献小的局部估计,从而减少节点的能耗以延长整个网络的生命周期.给出基本假设H0和H1,分别表示观测节点被放弃和被选中两种情况,p(Xk|H0)和p(Xk|H1)表示k时刻两种假设下的似然概率,则簇头节点的判决模型可描述为[20]

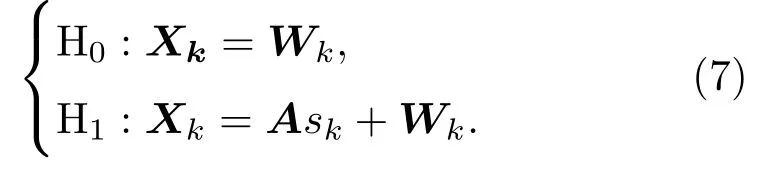
引理1 假设源信号sk、观测信号Xk和观测噪声Wk在各观测时刻k相互独立,则对数似然比函数为

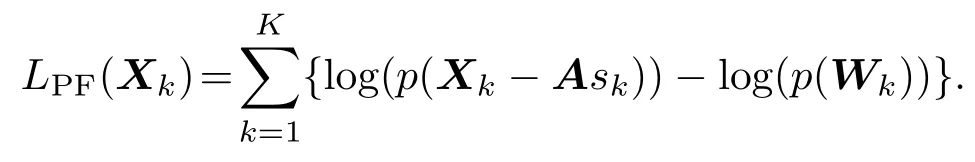
证明 由于sk,Xk和Wk在各时刻k相互独立,可知

为了构造广义似然比函数,利用H0和H1两种假设下的代价增量和来代替(10)式中的概率密度函数,可得归一化后的广义似然比判决函数：

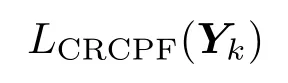
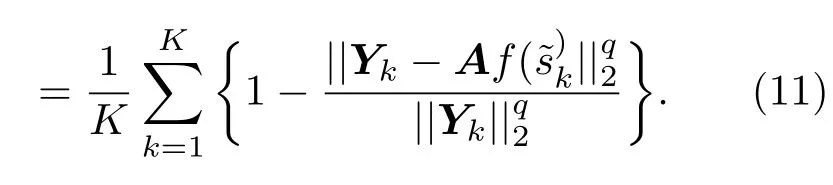
在实际的应用中,根据精度需求设定适当的判决门限ξ,当LCRCPF(Yk)≥ξ时,接受假设H1,此时观测节点被选中并发送估计的局部重构信号;当LCRCPF(Yk)＜ξ时,接受假设H0,放弃发送局部重构信号.

3.2 CRCPF重构算法

混沌信号的概率分布函数比较复杂,因此本文采用均匀量化方法对观测信号进行量化处理.CRCPF重构算法利用容积点积分变换来提高粒子的估计精度,通过簇头节点的局部估计信号和观测信号构造出广义似然比判决函数.基于状态观测方程(1)和(3),以容积点变换和代价参考粒子滤波为基础的信号重构算法流程如下.

1)粒子初始化

在粒子初始化过程中,通过对覆盖初始状态s0的有界区域进行采样,获得Np个初始样本粒子样本空间的粒子以均匀概率与初始状态相等.初始采样粒子必然包含源信号真实状态,即可设初始样本粒子的代价值为假设其对应的状态初始方差已知,从而得到初始样本粒子代价集

2)粒子重采样

k时刻,计算容积点[21]：

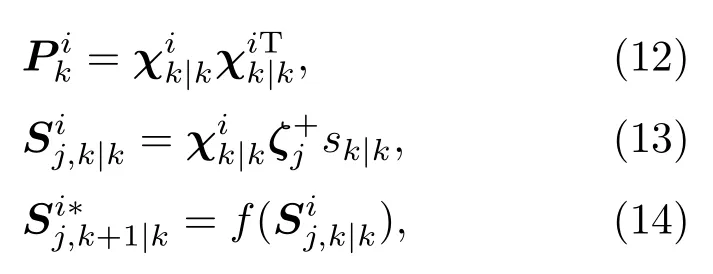
其中,j=1,2,···,2n,n是被积向量的维数,是噪声方差的平方根分解值.是容积点变换基础集[1]的第j个元素,基础集[1]定义为

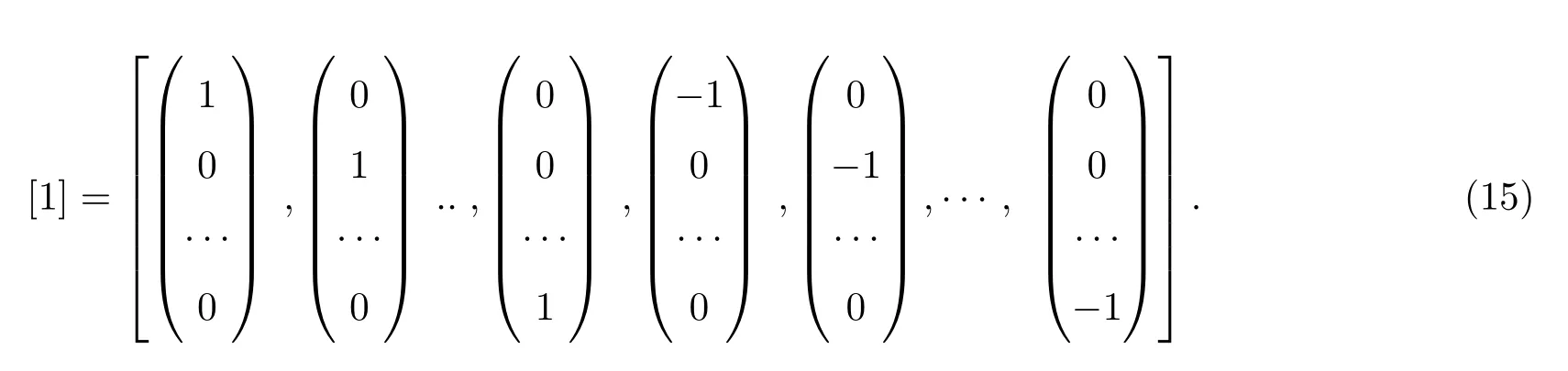
则粒子的时间更新和测量更新过程如下：

其中,ωj=1/2n是积分点的权重,Qk和Gk+1是过程噪声方差和测量噪声方差,在算法执行过程中被用户假设为服从一定的概率分布.粒子风险由(5)式计算得出,相对应的估计粒子由重采样得到,则k+1时刻的状态估计粒子集为

3)粒子传播和代价更新

k+1时刻,粒子集由进行更新,相应的粒子代价由(4)式更新.其中,表示均值为和方差为的高斯概率密度函数.

4)簇头上的信号局部重构

可得到j个簇头的局部重构信号

5)广义似然比判决的全局重构

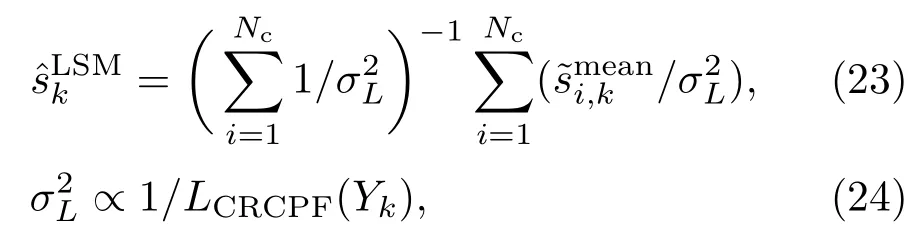
其中,Nc为经广义似然比判决所选择的工作节点个数,由各簇头节点上的广义似然比映射得出,为在融合中心上实现全局重构信号.重构算法在满足重构精度需求下,可以降低传感器网络的整体能耗,但一定程度上牺牲了信号重构的实时性.

3.3 算法复杂度和耗能分析

设信号的采样长度为K,粒子数量为Np,通过对比可得CPF,CRPF和CRCPF三种算法的复杂度为：

因此,CRCPF算法的复杂度与CPF算法相当.

文献[22]给出了传感器网络的能耗模型,耗能总量可近似为Etotal≈KMi[Eelec+εmpNcd4n].其中,Mi为量化比特,dn为簇头节点到融合中心的距离,Eelec和εmp为能耗常量.由此可知,传感器网络的整体耗能与K,Mi,dn和Nc均成正相关.单个簇结构耗能与d4n成正相关,当较大时,可忽略掉簇成员的能耗.选择到的工作节点数量Nc与广义似然比函数值成负相关,则传感器网络的整体能耗与广义似然比的判决阈值成负相关,即Etotal∝1/ξ.

4 仿真结果

本文采用的源混沌信号映射方程为sk+1=cos(4acos(sk)).为衡量所提算法的重构性能,定义均方误差MSE(mean square error,MSE)来定量计算：

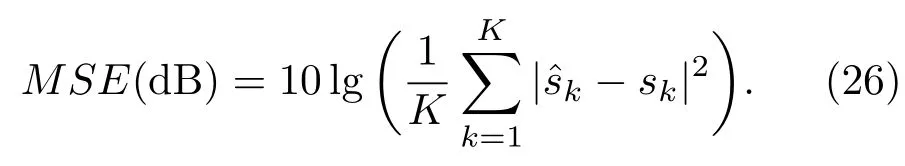
在仿真实验中,通过观察源信号与重构信号的波形设定MSE=-15 dB作为算法重构成功的参考基准.参照文献[11],将传感器均匀分布在50 m×50 m的平面上,数据融合中心距离感知区域dn=1000 m.为了检验算法的适用性和稳定性,设混合系数矩阵A随机产生,其他参数设定为λ=0.75,δ=1/Np,β=2和q=2,粒子总数Np=200,能耗参数Eelec=50 nJ/bit,εmp=0.0013 pJ/bit·m4.为保证仿真结果的可靠性,MSE值取500次蒙特卡罗仿真的均值,系统的观测噪声由(27)式给出.

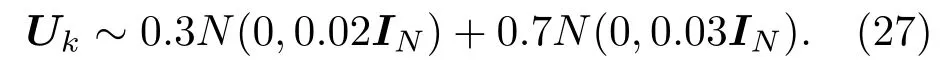
因量化噪声未知,只能用观测噪声来近似代替整体噪声.图1为当信号样本长度K=200,量化比特M和节点数量N=5,且整体噪声与观测噪声匹配时CRPF和CRCPF算法的重构结果.两种算法的平均MSE分别为-18.8962 dB和-22.2409 dB,实验验证了本文所提CRCPF算法的有效性,同时说明加入容积点变换可以提高算法的重构精度.此外,两种算法的平均单位信号处理时间为0.0767 s和0.0827 s,其比值与复杂度比值相近.为研究算法的重构性能和有簇模型下的网络能耗,进一步设计了噪声统计特性已知和未知两种情况.

图1 源信号和重构信号Fig.1.Source signal and reconstructed signals.

4.1 噪声统计特性已知

设实验过程中的各个分簇中观测噪声为服从(27)式的高斯分布,观测节点为N=300,节点平均分为100个簇,每个簇包含3个节点,仅簇头节点发送局部重构信号至融合中心.

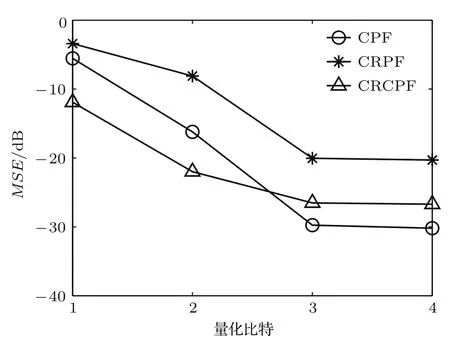
图2 噪声已知时MSE和量化比特的关系Fig.2.MSEversus quantization bit in the case of known noise.

图2和图3是当广义似然比判决门限ξ=0.75时,算法的MSE、网络耗能Etotal和量化比特Mi的对比关系.实验结果表明,在量化比特Mi=1时,三种算法均不能得到有效的工作节点,因此网络没有能耗;随着Mi增大,三种算法的重构精度均有所提升,重构成功率如表1所列.当Mi≤2时,CRCPF算法的性能优于CPF,是因为当量化噪声较大时,CPF算法的重采样概率的递推精度受到了较大影响;当量化比特Mi≥3时,三种算法的重构性能均有较大提升,但是以增加节点负载和计算量为代价.

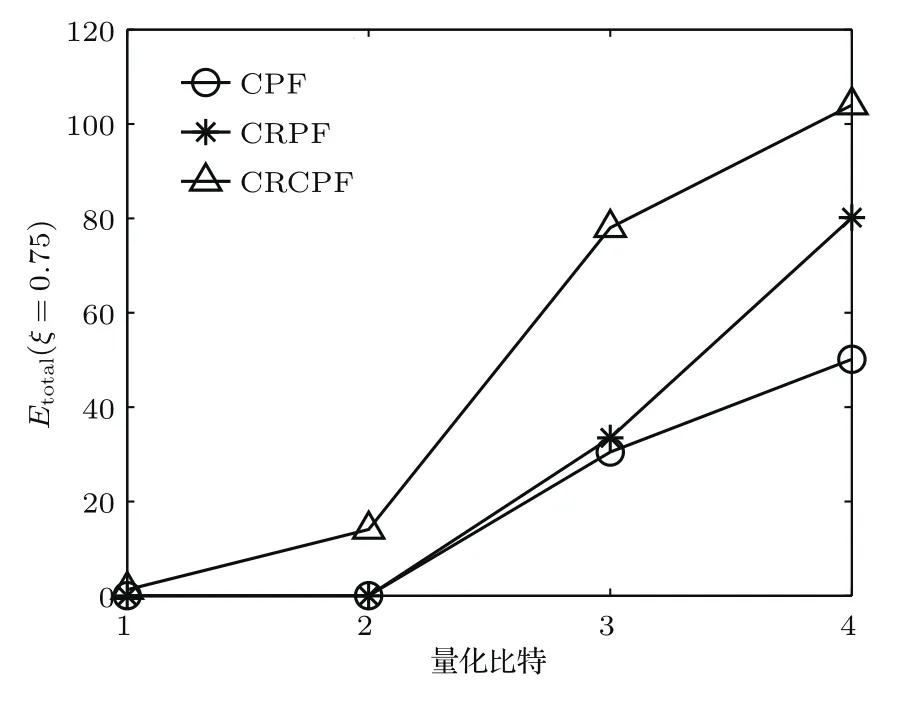
图3 噪声已知时网络耗能和量化比特的关系Fig.3.Energy consumption versus quantization bit in the case of known noise.

表1 噪声已知时算法在各量化比特下的成功率Table 1.Success rate versus quantization bit in the case of known noise.

图4 噪声已知时MSE与ξ的关系Fig.4.MSEversusξin the case of known noise.

图4和图5为当量化比特Mi=4,三种算法的MSE、网络耗能Etotal和广义似然比判决门限ξ的对比关系.随着ξ增大,被选中的簇头工作节点减少,从而导致算法的重构精度MSE有所下降.由图4可知,在ξ≤0.82时三种算法的MSE变化不大,说明被选中节点的少量减少对算法的重构性能影响不大;图5从传感器网络的能耗角度验证了算法性能的下降特性.

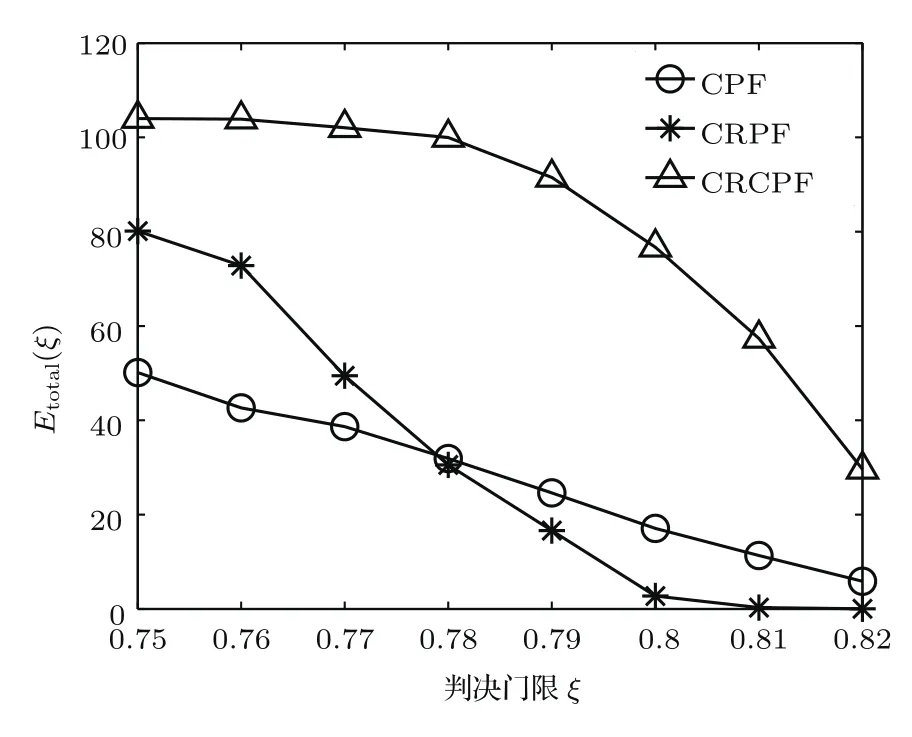
图5 噪声已知时网络能耗与ξ的关系Fig.5.Energy consumption versusξin the case of known noise.

4.2 噪声统计特性未知

相对于CPF算法,本文所提出的CRCPF算法不依赖于系统噪声的先验知识,具有更好的适用性和健壮性.本组实验中各个分簇的真实测量噪声由(27)式产生,整体噪声未知而被假设为服从高斯分布N(0,0.1I3).

图6 噪声未知时MSE与量化比特的关系Fig.6.MSEversus quantization bit in the case of unknown noise.

图6为当ξ=0.75,三种算法的MSE与量化比特Mi的关系.对比前一组实验可知,CPF算法具有一定的健壮性,但同等条件下CRPF和CRCPF算法的重构性能要优于CPF算法.网络能耗方面,当量化比特Mi≤2时三种算法均不能成功重构源信号,有效的簇头节点个数为零,即网络能耗Etotal近似为零;当Mi≥3时三种算法均能成功重构源信号,其有效簇头节点数为100,即网络能耗Etotal为最大.

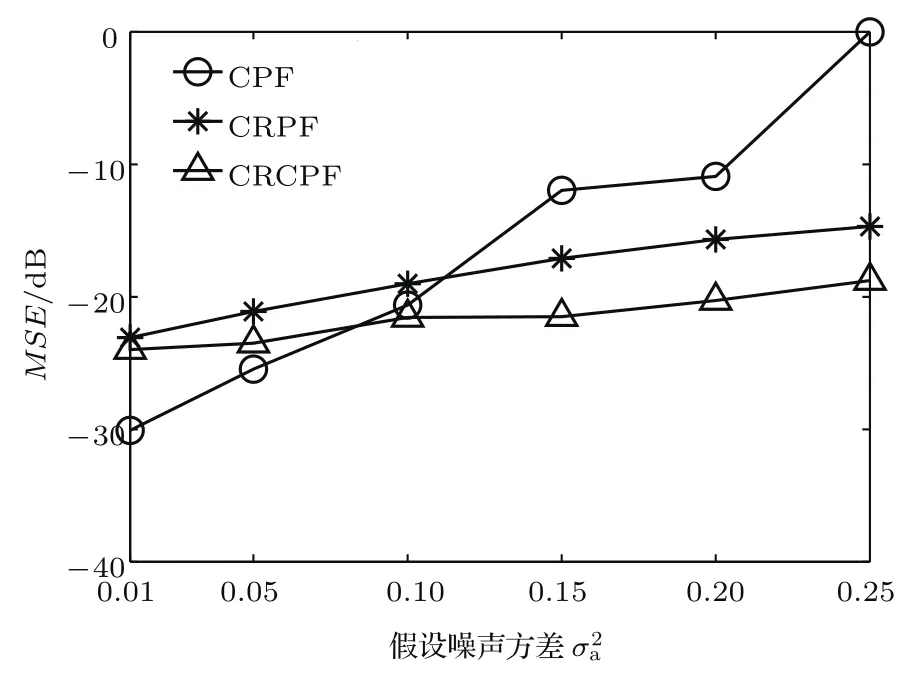
图7 正态分布：噪声未知时MSE与σ的关系Fig.7.Normal distribution：MSEversusσin the case of unknown noise.

图8 正态分布：噪声未知时网络耗能Etotal和σ的关系Fig.8.Normal distribution：energy consumptionEtotalversusσin the case of unknown noise.

图7和图8为当量化比特Mi=4和ξ=0.75时,三种算法的MSE、网络耗能Etotal与假设的系统噪声方差的关系.由实验结果可知,当假设的噪声水平与实际噪声值接近时,三种算法的重构精度和成功率均较高;当假设的噪声水平远离实际值时,CRPF算法和CRCPF算法仍能获得较好的重构精度和成功率,其重构成功率列于表2.

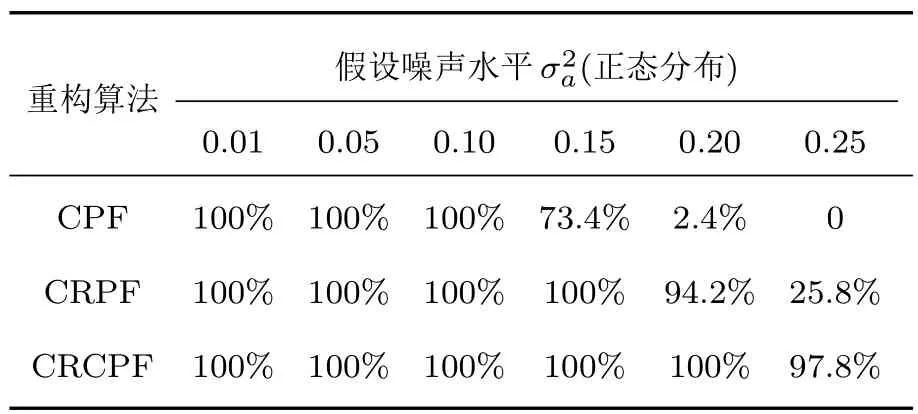
表2 噪声未知时算法成功率与假设噪声水平关系表Table 2.Success rate versus assumed covariance in the case of unknown noise.

图9 随机分布：噪声未知时MSE与σ的关系Fig.9.Random distribution：MSEversusσin the case of unknown noise.

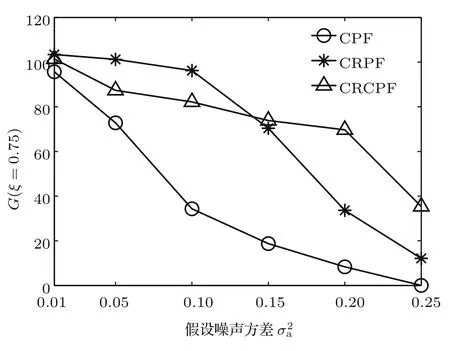
图10 随机分布：噪声未知时网络耗能Etotal和σ的关系Fig.10.Random distribution：energy consumptionEtotalversusσin the case of unknown noise.

为验证所提算法的可靠性和有效性,本文进一步采用区间[-0.05,0.05]上随机分布的观测噪声Uk对其进行测试.在算法执行过程中,噪声统计特性被假设为满足方差参数σ的正态分布.图9和图10为当量化比特Mi=4和ξ=0.75时,三种算法的MSE、网络耗能Etotal与假设的系统噪声方差σ的关系.对比前一实验可知,本文所提CRCPF算法对噪声统计特性相对不敏感,随着所假设的系统噪声方差σ的增大,CRCPF算法的性能要优于CPF算法和CRPF算法.理论上贝叶斯估计是一个预测-修正-预测的迭代过程,图7和图9的仿真结果说明当假设噪声与实际噪声不匹配时,粒子的估计误差将会在算法中被叠加放大,从而导致算法性能下降,甚至不能重构出源信号.

5 结 论

针对传感器网络中噪声未知情况下的混沌信号重构问题,以容积点变换和代价参考粒子滤波器为基础,提出了一种不依赖于噪声统计特性的重构方法,进一步通过广义似然比函数的映射判决完成簇头节点的选择.仿真结果表明,CRCPF算法在噪声统计特性已知和未知情况下,均能有效重构源混沌信号;而当假设噪声与实际噪声不匹配时,CRCPF算法的性能明显优于传统的粒子滤波算法.此外,算法通过选择不同的广义似然比判决阈值可以实现网络能耗和重构精度的折中,具有更好的健壮性和适用性.在实验中,本文只考虑了网络平均分簇的情况,对于节点生命周期和网络传输中数据丢失情况下的信号重构问题,将是下一步的研究方向.

[1]Rawat P,Singh K D,Chaouchi H,Bonnin J M 2014J.Supercomput.68 1

[2]Qi H,Wang F B,Deng H 2013Acta Phys.Sin.62 270(in Chinese)[祁浩,王福豹,邓宏2013物理学报 62 270]

[3]Sun B,Ahmed F,Sun F,Qian Q,Xiao Y 2016Int.J.Sensor Networks20 26

[4]Galka A,Wong K K F,Stephani U,Ozaki T 2013Int.J.Bifurcat.Chaos23 1350165

[5]Hao X C,Liu W J,Xin M J,Yao N,Ru X Y 2015Acta Phys.Sin.64 080101(in Chinese)[郝晓辰,刘伟静,辛敏洁,姚宁,汝小月2015物理学报64 080101]

[6]Chen H B,Tse C K,Feng J C 2008IEEE Trans.Circ.Syst.II:Express Briefs55 947

[7]Wang S Y,Feng J C 2008J.Electron.Inform.Technol.30 89(in Chinese)[王世元,冯久超2008电子与信息学报30 89]

[8]Hu Z H,Feng J C 2010J.Southwest Univ.(Natural Science Edition)32 146(in Chinese)[胡志辉,冯久超 2010西南大学学报(自然科学版)32 146]

[9]Wang S Y,Feng J C 2012Acta Phys.Sin.61 170508(in Chinese)[王世元,冯久超 2012物理学报 61 170508]

[10]Naqvi S M,Yu M,Chambers J A 2010IEEE J.Select.Topics in Signal Process.4 895

[11]Chen H B,Feng J C 2010J.Southwest Univ.(Natural Science Edition)32 124(in Chinese)[陈宏滨,冯久超2010西南大学学报(自然科学版)32 124]

[12]Huang J W,Feng J C 2014Chin.Phys.B23 070504

[13]Chen H B,Tse C K,Feng J C 2009IEEE Trans.Parall.Distrib.Syst.20 886

[14]Míguez J,Bugallo M F,Djurić P M 2004EURASIP J.Adv.Signal Process.2004 2278

[15]Míguez J 2007Signal Process.87 3155

[16]Míguez J 2007Digit.Signal Process.17 787

[17]Lu J,Shui P L,Su H T 2014IET Signal Process.8 85

[18]Hu Z T,Pan Q,Yang F,Cheng Y M 2009Systems Engineer.Electron.31 3022(in Chinese)[胡振涛,潘泉,杨峰,程咏梅2009系统工程与电子技术31 3022]

[19]Shui P L,Shi S N,Lu J,Jiang X W 2016Digit.Signal Process.48 104

[20]Lu J,Su H T,Shui P L,Zhou Z G 2013J.Xi’an Jiaotong Univ.47 93(in Chinese)[卢锦,苏洪涛,水鹏朗,周忠根2013西安交通大学学报47 93]

[21]Arasaratnam I,Haykin S 2009IEEE Trans.Autom.Control54 1254

[22]Heinzelman W B,Chandrakasan A P,Balakrishnan H 2002IEEE Trans.Wireless Commun.1 660

PACS:05.45.—a,05.45.Vx,84.40.Ua DOI:10.7498/aps.66.040503

Reconstruction algorithm of chaotic signal based on generalized likelihood ratio threshold-decision∗

Ren Zi-Liang1)2)Qin Yong2)Huang Jin-Wang2)Zhao Zhi1)Feng Jiu-Chao1)†
1)(School of Electronic and Information Engineering,South China University of Technology,Guangzhou 510641,China)
2)(School of Computer Science and Network Security,Dongguan University of Technology,Dongguan 523808,China)

7 September 2016;revised manuscript

20 November 2016)

Blind signal reconstruction in sensor arrays is usually a highly nonlinear and non-Gaussian problem,and nonlinearfiltering is an effective way to realize state estimation from available observations.Developing the processing problem of blind signal in wireless sensor networks(WSNs)will greatly extend the application scope.Meanwhile,it also meets great challenges such as energy and bandwidth constrained.For solving the constrained problem in WSNs,the observed signals must be quantified before sending to the fusion center,which makes the overall noise unable to be modeled accurately by simple probabilistic model.

To study the reconstruction issue of chaotic signal with unknown statistics in WSNs,a reconstructed method of chaotic signal based on a cost reference particle filter(CRPF)is proposed in this paper.The cost recerence cubature particle filter(CRCPF)algorithm adopts cubature-point transformation to enhance the accuracy of prediction particles,and cost-risk functions are defined to complete particle propagation.The effectiveness of proposed CRCPF algorithm is verified in the sensor network with a fusion center.Moreover,a generalized likelihood ratio functionis obtained by the cost increment of local reconstructed signals in the cluster-based sensor network topology model,which is used to reduce the network energy consumption by selecting working nodes.Simulation results show that compared with CPF and CRPF,the proposed algorithm CRCPF attains good performance in a WSN with unknown noise statistics.Meanwhile,the CRCPF algorithm realizes the compromise between energy consumption and reconstruction accuracy simultaneously,which indicates that the proposed CRCPF algorithm has the potential to extend other application scope.

cost reference,chaotic signal reconstruction,energy consumption,generalized likelihood ratio

:05.45.—a,05.45.Vx,84.40.Ua

10.7498/aps.66.040503

∗国家自然科学基金(批准号：60872123)、国家自然科学基金委员会广东省自然科学基金联合基金(批准号：U0835001)和广东省高校科技创新计划基金(2013KJCX0178)资助的课题.

†通信作者.E-mail：fengjc@scut.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant No.60872123),the Joint Fund of the National Natural Science Foundation and the Natural Science Foundation of Guangdong Province,China(Grant No.U0835001),and the Guangdong Higher School Scientific Innovation Project,China(Grant No.2013KJCX0178).

†Corresponding author.E-mail：fengjc@scut.edu.cn