周期波动性对金融市场稳定性的影响∗

周若微 李江城2)董志伟 李云仙2) 钱振伟

1)(云南财经大学金融学院巨灾风险管理研究中心,昆明 650221)

2)(云南大学统计系,昆明 650091)

周期波动性对金融市场稳定性的影响∗

周若微1)李江城1)2)†董志伟1)李云仙1)2)钱振伟1)

1)(云南财经大学金融学院巨灾风险管理研究中心,昆明 650221)

2)(云南大学统计系,昆明 650091)

(2016年5月23日收到;2016年11月29日收到修改稿)

利用平均逃逸率和逃逸时间分别研究了周期性波动对股票价格稳定性在金融常态和金融危机下的影响.基于Heston模型、引入单稳势函数和周期函数,构建了描述股票价格处于稳定状态和崩盘的逃逸状态的动力学模型.通过数值模拟和实际数据结合,发现：1)利用道琼斯指数成分股的实际金融数据对模型参数进行估计,对模型和实际金融数据的概率密度函数做了比较,发现模型和实际情况较为符合;2)从金融常态到金融危机逃逸率的研究中,发现较强的经济增长率、较小的周期波动强度、较小的长期波动值和较弱的波动的振幅都会增强股票价格处于稳定状态的机率;3)通过研究金融危机周期性波动对价格平均逃逸时间的影响,发现存在一个最佳的周期波动振幅能最大化股票价格稳定性,某个最佳的波动均值回归速度、变弱的周期波动频率、变强的噪声关联强度和增加的经济增长率会进一步加强该最佳周期波动振幅从而进一步促进稳定性.

周期波动,平均逃逸时间,逃逸率,金融物理

1 引 言

物理学研究发现随机共振和逃逸现象是自然界中非常常见的现象.随机共振[1]在诸多领域被广泛地发现和研究,例如双稳系统[2-5]、线性系统[6]、生物系统[7]、生态系统[8,9].在对逃逸现象的研究中,平均逃逸时间,也就是平均首通时间是一个常被采用的物理量[10-14].Bonanno等[10]在研究单稳势中粒子逃逸现象时发现了噪声增强稳定性行为.Fiasconaro和Spagnolo[11]研究了一个过阻尼的粒子受到色噪声驱动从亚稳态逃逸的过程,同样发现了噪声增强系统的稳定性行为.Jia[12]利用平均首通时间研究了受关联噪声驱动的延迟双稳系统中时间延迟对瞬态行为的影响.Yoshimoto等[13]讨论了Belousov-Zhabotinsky化学反应的混沌变化中噪声增强有序性的行为.Zeng等[14]研究了活跃的布朗粒子的逃逸和共振行为,也发现了噪声增强稳定性现象.在金融系统中也发现了随机共振现象和逃逸现象.如 Krawiecki和Holyst[15]用随机共振描述股票市场崩盘和泡沫,Babinec[16]研究了交互代理模型中的随机共振现象,Li和Mei[17]发现了金融市场中的逆共振现象及随机共振中的延迟作用.Heston模型与逃逸时间被广泛应用于金融危机中股票价格动力学变化的研究,如用单稳势函数的方法研究了修正的Heston模型中的均值逃逸时间[18,19]、对证券市场发展中的不同模型中冲击时间的统计特征[10,20]、华尔街市场证券价格收益率逃逸时间的统计特征[11]、平均逃逸时间和生存率的准确表达[21,22]等.现今利用物理的方法和工具、复杂性科学、网络科学和数据挖掘技术来对社会经济系统中的各种问题(如金融市场)进行分析建模取得了不少成果,并兴起了一个逐渐成长的研究方向——金融物理学[23].

与此同时,股票市场价格的波动性是有别于风险和收益的一个重要的研究热点.投资者的资产配置和投资行为等信息往往也是通过股市波动性在市场中传导的.对股票价格波动特征的研究[24]、衍生工具定价[25]、风险控制[26]、市场监管和价格预测[27]等金融市场的重大研究课题都具有极其重要的意义.波动性使得金融市场时间序列表现出尖峰肥尾[28]、长期记忆和波动性集聚[29]等统计学特征.Bollerslev[30]提出了广义自回归条件异方差波动率结构.Ding等[31]对标普500指数收益率的开创性研究发现波动率表现出很强的长期记忆性,具有波动持久性.Bansal等[32]指出波动性对资产定价和宏观经济有着重大的作用.Jebabli等[33]在世界股票市场和油价冲击对食物价格的影响的研究中发现了波动溢出现象.Heston模型[34]也能够很好地描述金融市场肥尾、长期记忆和波动性集聚等统计学特征.Forde等[35]基于Heston模型研究了隐含波动率的期限结构.Drǎgulescu和 Yakovenko[36]基于Heston模型和随机波动研究了收益的概率密度分布.特别是波动性集聚表现出明显高波动和低波动周期性交换的特征.Poon和Granger[37]评论了波动性的研究并指出了盘中周期性波动的特征.Fouque等[38]利用渐进定价理论研究了标普500指数的隐含波动率,解释了伴有时间周期波动的潜在价格动力学行为.因此,股票价格波动性变化在金融市场中具有重要的意义,值得深入讨论.

本文结合物理中共振和逃逸的思想,应用Heston模型描述股票价格的动力学,综合地研究股票市场中价格的周期波动性对市场稳定性的影响.文中结构如下：第二部分引入周期性波动,建立周期波动的Heston模型;第三部分比较了所构建模型和实际数据的概率密度函数;第四部分用共振的思想研究一个波动周期内系统出现危机的比率;第五部分利用价格平均逃逸时间讨论周期波动性对市场稳定性的影响;第六部分为总结.

2 周期的Heston模型

由前面的讨论可以发现Heston模型能很好地描述股票价格的动力学变化过程,因而股票价格的动力学模型可以用下面简化的Heston模型的随机微分方程组来表示[34,36]：

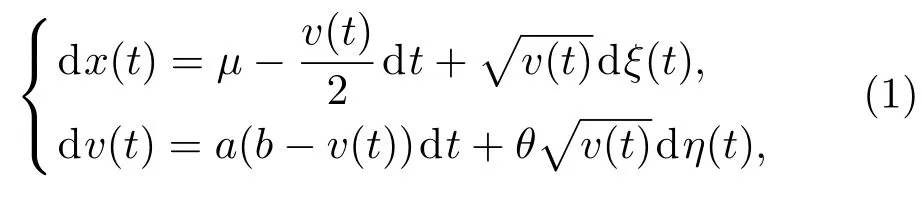
其中x(t)表示对数股价,µ为经济增长率,a表示回归v(t)的均值回归速度,b是v(t)的长期方差,θ为波动率振幅.v(t)是一个时间为a-1的指数瞬变过程,并且向b靠近[39].ξ(t)和η(t)是两个相关的维纳过程,满足以下条件：

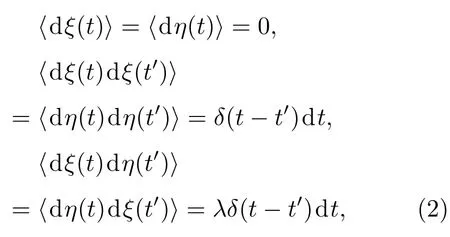
λ是ξ(t)和η(t)的相关系数.尽管在文献[17]中分别讨论了外部和内部的周期信息对金融系统的影响,然而股票市场是一个复杂的系统,公司的股票价格一直会受到市场外部宏观经济的影响和公司自有的内部周期性信息的作用.内外周期性信息的共同作用下,必然导致股票价格的波动性,这会使得股价波动表现出高波动和低波动周期性交替变换的波动集聚特征.如对经济代理两个行为模式的研究发现,行为切换会导致大的波动和生成总体波动性集群,表现出周期特征[40].因而波动率振幅θ因受内外周期性作用,其中必然包含有周期性特征.而这样的周期特征可以展开为傅里叶级数的形式：

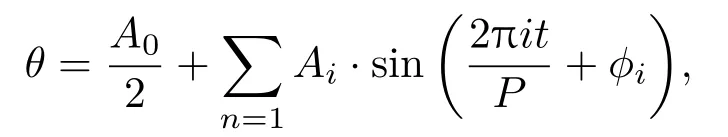
其中A0,Ai,P,φi为展开参数.为了研究的简便,本文主要研究一级展开,即使用c+Acos(Ωt+φ)来简化替换方程(1)中的θ,Acos(Ωt+φ)便是内外周期性信息对股价波动性的作用.A,Ω和φ为波动周期性的振幅、频率和初始相位,c为波动率振幅θ的期望,波动的周期性围绕c在变化.方程(1)变为

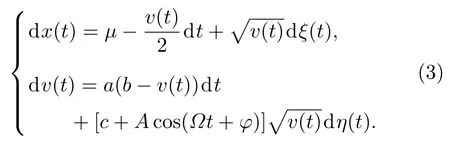
金融系统中股价在一定的价格区域内,多空双方力量平衡时表现出盘整的特征.当信息和市场中的投资者的行为发生共振现象时,投资者往往表现出羊群行为,促使股价单方面暴涨和暴跌.当共振行为超出一定的阈值,整个市场会出现不可逆转的股价严重泡沫和崩盘现象,进而引发整个系统的危机.在此我们采用文献[18,19]中的单稳势函数U(x)来描述这个过程,详见图1.U(x)=px3+qx2,p=2和q=3.U(x)是单稳势函数,x=-1的虚线分为左右两个区域,粒子如果落入x≥-1的区域是相对稳定区域,系统往往处于动态稳定,这和股价处于常态类似;反之如果落入x＜-1的区域,粒子很大概率上处于单方面往左区域逃逸,这与股价崩盘是非常类似的.股价如果在右边势阱中,则股票价格处于较为稳定的区域.当市场中共振行为使得股价波动性越过左边不稳定态的顶端时,股价会趋于不稳定的状态,极大可能会出现崩盘效应.因而受周期波动性和单稳势函数影响的动力学方程可以变为如下形式：

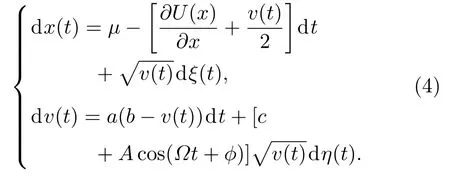
基于文献[36]和极值理论的方法,与文献[17]相似,考虑小周期波动和低频周期,选择和文献[17]中一样的参数值：A=0.05,Ω=0.05,我们对方程(4)进行参数估计.数据采用的是道琼斯工业指数30只成分股在2007年9月3日到2008年12月31日,共计70637个样本.与数据匹配,考虑从危机初期开始,和亚稳态位置类比,故而随机模拟方程(4)时,采用初始位置x=-1到结束位置x=-6为止.可以得到µ,λ,a,b和c参数估计值分别为=0.0162593,=0.189739,=2.30123,=0.00256536 和=0.013307.

图1 股票对数价格的单稳势函数图Fig.1.Cubic potential used in the dynamical equation for the price.

3 价格收益的概率密度函数

在本节中,为了测试第2部分的假设合理性,我们比较了模型和时间数据的股票价格收益的概率密度函数.采用文献[41,42]中的描述,股价的日收益可以定义为

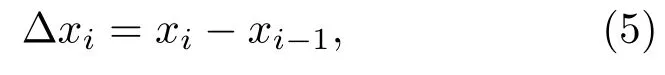
其中xi是在第i个时间点的对数价格(i=1,2,3,···).

为了比较收益 Δxi的概率密度函数 (PDF),我们采用第2部分估计得到的参数进行模拟.由方程(2),采用Box-Muller的方式模拟高斯白噪声.时间步长为Δt=0.01,每一个步长当作一个交易周期单位,如果采用的是日数据,则可以理解为一天.基于方程(4)和(5),模拟超过106个路径,最后得到收益的PDF.对于实际金融数据,也采用第2部分提到的道琼斯工业指数30只成分股从2007年9月3日到2008年12月31日7万多个交易日的每日复权的收盘价;对复权收盘价先求对数,后用方程(5)的方法求出70637个对数日收益率样本,再用频数法求出收益的PDF(组间距离为0.01).两个结果比较后呈现在图2中,可以发现实际数据和模型模拟得到的结果非常符合.

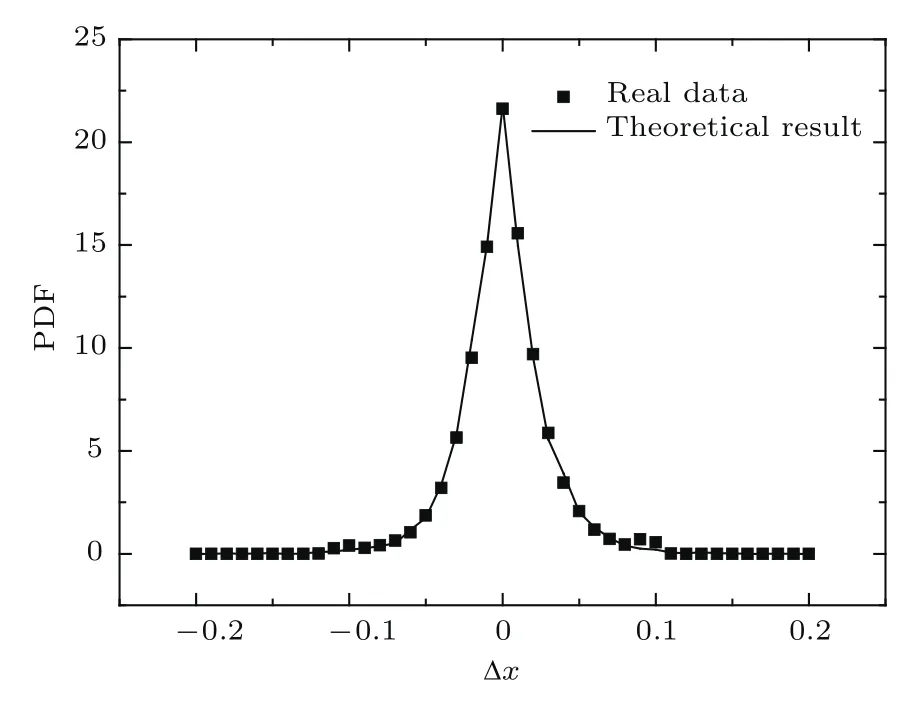
图2 基于Heston模型和真实数据集的收益概率密度函数比较Fig.2.Probability density functions of price returns for a simulated data set from the Heston model and a real market data set.

4 周期逃逸率

前面已经论述了波动周期性的变化会表现出波动集聚的特征.只要波动不大于某个临界值,股票价格如果初期处于稳定状态,也就是如粒子初期处于图1右边区域势阱中,会一直持续稳定下去.但是,如果投资者的恐惧和贪婪驱动下的交易行为,与内外周期信息驱动的周期性波动性发生同步共振现象,会放大波动性,驱使股票波动性超越某个阈值,逃逸出右边的势阱,进入左边逃逸区域.为了研究哪些因子会诱发这个逃逸行为,我们使用布朗粒子来描述股价的随机波动.研究从稳态 (x=0)出发,逃逸到明显已经进入左边区域(x≤-6.0)粒子的比率,也就是从股市稳定到发生股票崩盘现象的概率.鉴于波动的周期性,我们研究了一个周期内从稳定态逃逸到崩盘区域的逃逸率,也就是平均周期逃逸率(mean periodic escape rate,MPER).具体计算方法：给定初始位置x0=0,用图2的方法基于方程(2)和(4)模拟股价的轨迹.考虑Δt=0.01为一个交易日,计算一个周期股价的路径,由方程(4)中Ω求出一个周期为个交易日.一个周期结束,股票价格如果为x≤-6.0,则记为一次逃逸,反之则记为处于稳定区域.而后重新开始计算路径,总共计算超过106条路径,用逃逸的总次数除以总路径量,计算出一个周期内平均逃逸的比率.

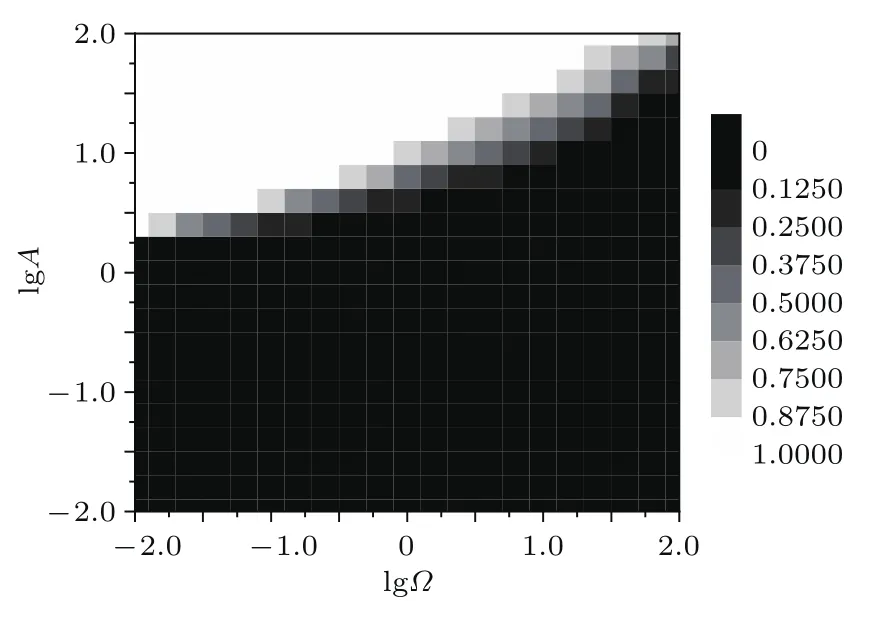
图3 MPER关于 lg(A)和 lg(Ω)的相位图Fig.3.The phase diagram of MPER vs.lg(A)and lg(Ω).

为了研究周期性波动对MPER影响,图3给出了 MPER关于 lg(A)和lg(Ω)的相位图.从图3中可以发现,随着对数周期波动性强度lg(A)的增加,黑色区域慢慢变为白色,也就是MPER逐渐增大.这也就是说,随着周期波动性强度增强,股票市场越不稳定.在高波动区域,对数周期波动性频率增强使得MPER减少.这是因为周期波动性频率增强减少了周期的长度.该相位图黑色区域是影响因子的安全区域,白色则是逃逸率100%的危险区域.由此,可以很方便地找到股票价格稳定性区域和不稳定区域.

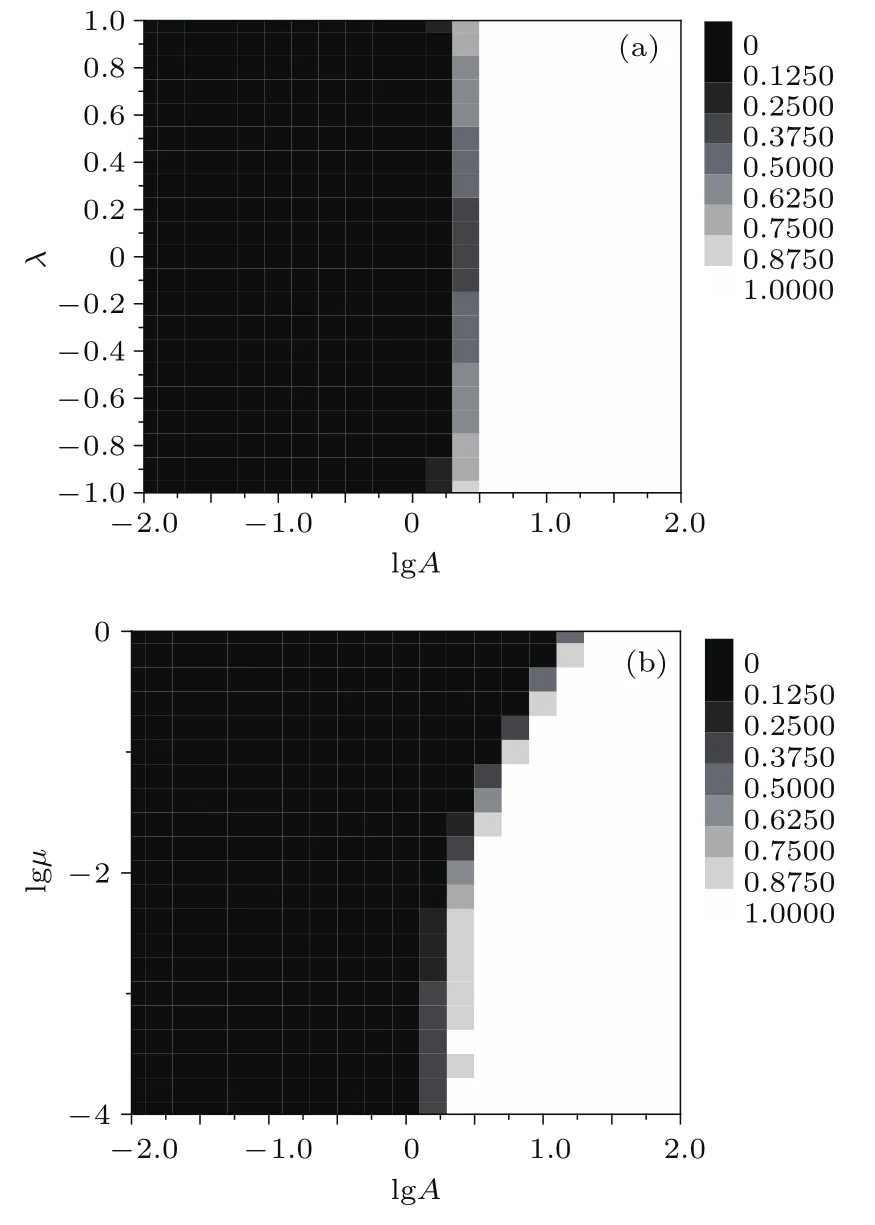
图4 MPER的相位图 (a)MPER关于lg(A)和λ的相位图;(b)MPER关于lg(A)和lg(µ)的相位图Fig.4.The phase diagrams of MPER：(a)The phase diagram of MPER vs.lg(A)andλ;(b)the phase diagram of MPER vs.lg(A)and lg(µ).

为了研究周期性波动、噪声关联强度和经济增长率对MPER影响,图4(a)和图4(b)分别给出了MPER关于lg(A)和λ的相位图以及关于lg(A)和lg(µ)的相位图.从图4(a)中可以发现,噪声关联强度λ对MPER影响是微弱的,基本不会改变黑色安全区和白色逃逸区的大小.两个区域的临界阈值主要由周期性波动强度A所决定.图4(b)则显示了增强的对数经济增长率会增大黑色安全区域的大小.

为了研究波动性的其他因子对MPER的作用,图5(a)给出了MPER关于lg(A)和lg(a)的相位图;图5(b)给出了关于lg(A)和lg(b)的相位图;图5(c)给出了关于lg(A)和lg(c)的相位图.图5(a)显示了增强的对数波动均值回归速度lg(a)会增大黑色安全区域的大小;图5(b)和(c)都显示了相同的特征,小的对数长期波动值lg(b)和波动的波动lg(c)使得股票价格处于黑色的安全区域,反之高的lg(b)和lg(c)诱导价格处于白色的逃逸区域.

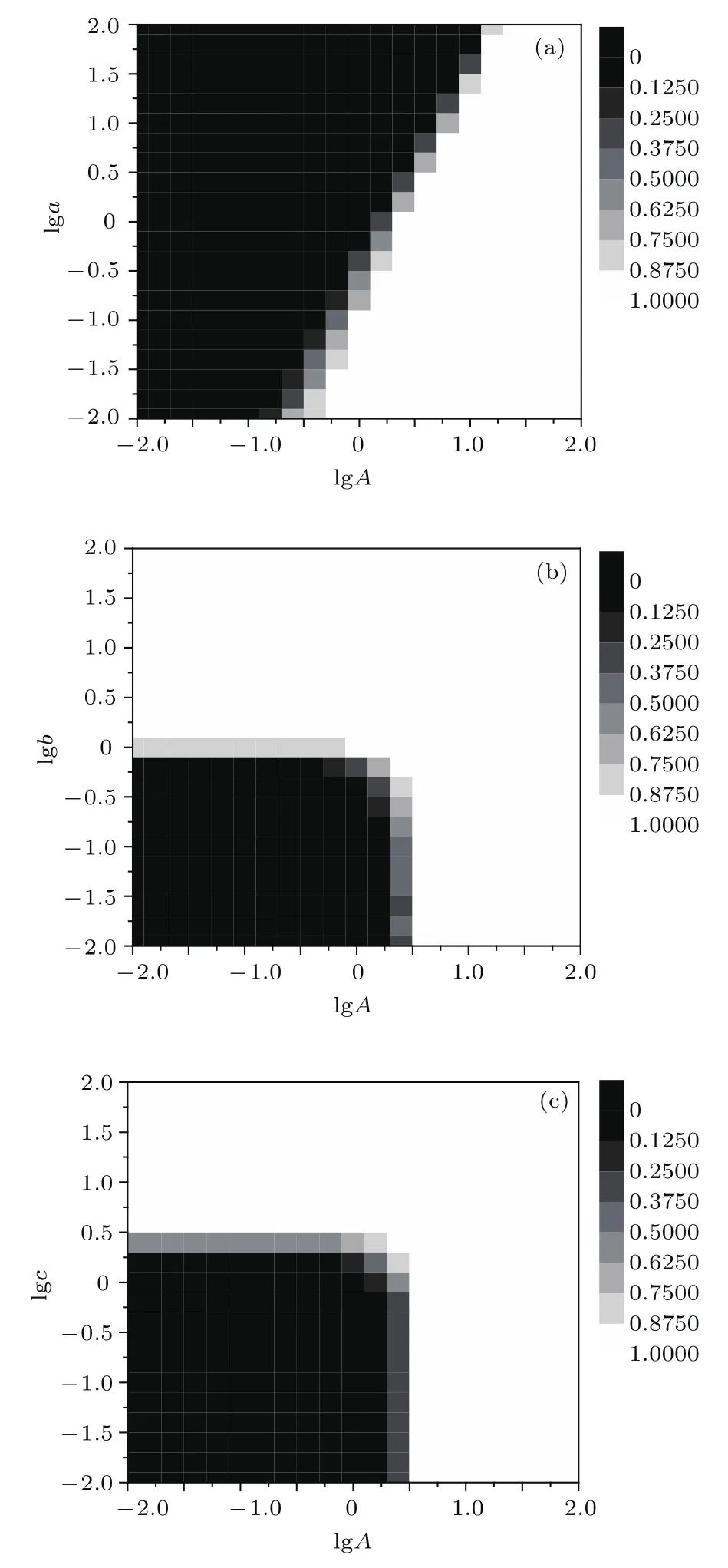
图5 MPER的相位图 (a)MPER关于lg(A)和lg(a)的相位图;(b)MPER关于lg(A)和lg(b)的相位图;(c)MPER关于lg(A)和lg(c)的相位图Fig.5.The phase diagrams of MPER：(a)The phase diagram of MPER vs.lg(A)and lg(a);(b)the phase diagram of MPER vs.lg(A)and lg(b);(c)the phase diagram of MPER vs.lg(A)and lg(c).

5 金融危机中的平均逃逸时间

如果股票价格处于第4部分中的白色区域,此时股价如同粒子逃逸一样容易往左边滑下去.这样的现象在金融市场中则表现为股价崩盘现象,进而引发金融危机.然而研究发现,噪声在某些条件下会表现出增强系统稳定性的作用.同样在金融危机时,周期性波动是否会增强系统的稳定性?为了研究在金融危机状态下周期性波动对金融系统稳定性的影响,我们使用平均逃逸时间(MET)来进行分析.考虑已经处于白色的逃逸区域,选择图1中左边区域的x=-1.25开始,到明显进入到金融危机的末期,股价已经严重贬值的x≤-6.0为止.由方程(2)和(4)得到平均逃逸时间.

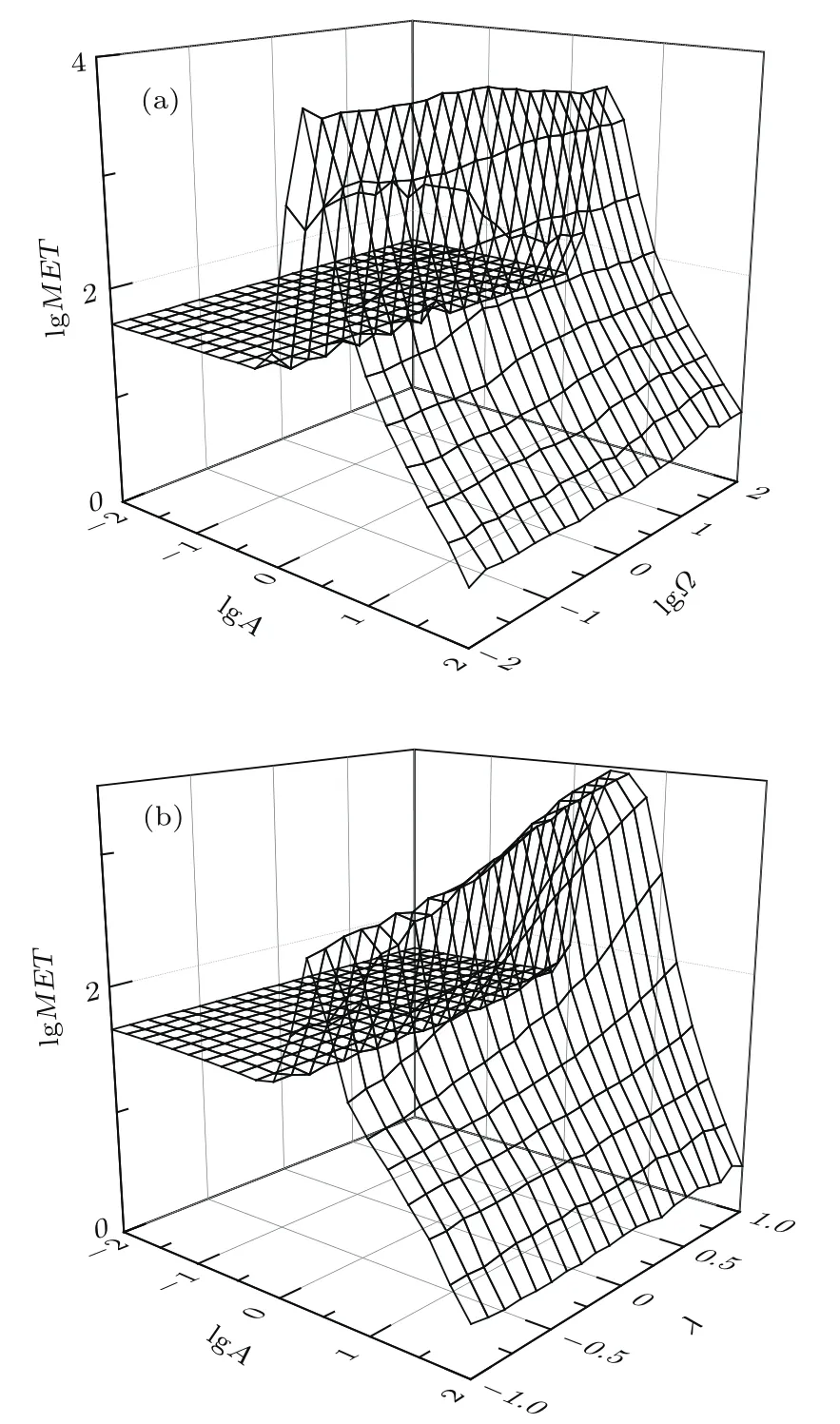
图6 对数平均逃逸时间 lg(MET) (a)lg(MET)关于lg(A)和lg(Ω)的函数;(b)lg(MET)关于lg(A)和λ的函数Fig.6.The function of lg(MET)：(a)lg(MET)vs.lg(A)and lg(Ω);(b)lg(MET)vs.lg(A)andλ.

为了分析周期波动性和噪声关联强度对MET的作用,图6(a)给出了对数平均逃逸时间lg(MET)关于 lg(A)和 lg(Ω)的函数;而图6(b)给出了关于 lg(A)和λ的函数.图6(a)和图6(b)都显示了lg(MET)vs.lg(A)存在着一个极大值,也就是说存在一个最佳的周期波动强度A使得平均逃逸时间最大(即最佳的A最大地增强了股票价格的稳定性).图6(a)显示了随着lg(Ω)的增大,lg(MET)vs.lg(A)的最大值在减小;反之,图6(b)显示了随着λ的增大,lg(MET)vs.lg(A)的最大值在增大.也就是说周期波动频率的增加减弱了股票价格的稳定性,而关联噪声强度的增加则加强了股票价格的稳定性.

图7 (a)对数平均逃逸时间 lg(MET)关于lg(A)和lg(µ)的函数;(b)MPER关于lg(A)和lg(µ)的相位图Fig.7.(a)The function of lg(MET)vs.lg(A)and lg(µ);(b)the phase diagram of MPER vs.lg(A)and lg(µ).

为了分析周期波动性和经济增长率对MET的影响,图7(a)给出了对数平均逃逸时间lg(MET)关于 lg(A)和lg(µ)的函数.从图7(a)中可观察到lg(MET)vs.lg(A)存在着一个最大值,而且随着lg(µ)的增大,lg(MET)vs.lg(A)的最大值在增大.当 lg(µ)取值较大时(特别是lg(µ)约大于阈值-1.7),增大的lg(µ)会驱动本来在逃逸过程的粒子进入到稳态区域,也就是说当经济增长率超过某个阈值的时候,粒子将很可能长久地留在稳定区域,使得平均逃逸时间趋近于无穷和平均周期逃逸率趋近于0.为了表明这个现象,MPER关于lg(A)和 lg(µ)的相位图呈现在图7(b)中.此时模拟的起始位置为x=-1.25和终止位置为x≤-6.0.图7(b)中显示了当经济增长率大于 10-1.7(约为2.0%)时,股票价格由即将进入金融危机的状态转换为稳定的经济状态.这和实际的经济状态是符合的,高速增长的GDP将会促进股票市场稳定.

图8 对数平均逃逸时间lg(MET) (a)lg(MET)关于lg(A)和lg(a)的函数;(b)lg(MET)关于lg(A)和lg(b)的函数;(c)lg(MET)关于lg(A)和lg(c)的函数Fig.8.The logarithmic mean elapsed time lg(MET)：(a)lg(MET)vs.lg(A)and lg(a);(b)lg(MET)vs.lg(A)and lg(b);(c)lg(MET)vs.lg(A)and lg(c).

为了分析波动性的其他因子对MET的作用,对数平均逃逸时间lg(MET)关于lg(A)和lg(a)的函数图见图8(a);对数平均逃逸时间lg(MET)关于lg(A)和lg(b)的函数图见图8(b);对数平均逃逸时间 lg(MET)关于 lg(A)和 lg(c)的函数图见图8(c).图8(a)—(c)都显示了lg(MET)vs.lg(A)存在着一个极大值.图8(a)还表明了lg(MET)vs.lg(a)也存在着一个最大值,而且这个最大值会进一步加强 lg(MET)vs.lg(A)的极大值.也就是说一个最佳的波动均值回归速度会最强地增加lg(MET)vs.lg(A)的极大值,也即最佳的波动均值回归速度和周期波动振幅会有互相加强的作用.图8(b)和图8(c)也都表明了在小的周期波动强度A下,lg(MET)vs.lg(b)和lg(MET)vs.lg(c)都存在一个最大值.lg(MET)vs.lg(A)的最大值的区域和这两个最大值类似,都在较小的对数长期波动值lg(b)和波动振幅lg(c).这和图5中的结果是相对应的.

6 结 论

本文研究了稳态区域和逃逸区域中周期性波动对股票价格稳定性的作用.我们应用Heston模型来描述股票价格的动力学过程;引入了一个稳态和一个亚稳态的单稳势函数来刻画股票价格处于稳定状态和崩盘的逃逸状态;在股票价格波动的振幅项中,引入了周期函数,刻画周期波动性.结合实际数据,采用了极值方法对参数进行了估计,对模型和实际金融数据的概率密度函数的比较结果较为符合.

基于共振的思想,采用了一个周期内从稳态到明显逃逸状态的逃逸率来描述股票价格从稳定状态到金融危机状态的概率,并研究了周期性波动对周期逃逸率的影响.通过相位图刻画了安全区域和危机区域的参数范围,发现较大的周期波动强度、较大的长期波动值和较强的波动的振幅都会诱导股票价格进入崩盘的危机状态;反之,较强的经济增长率、较小的周期波动强度、较小的长期波动值和较弱的波动的振幅都会增强股票价格处于稳定状态.

对于已经进入金融危机状态的股票价格稳定性,我们利用平均逃逸时间研究了周期性波动对稳定性的作用,发现分别存在一个最佳的周期波动振幅、波动均值回归速度、长期波动值和波动的振幅使得股票价格稳定性最强;同时最佳的波动均值回归速度和周期波动振幅会有互相加强的作用.在平均逃逸时间与周期波动振幅的函数中,增强的噪声关联强度和经济增长率会加强股票价格的稳定性;反之,增强的周期波动频率会减弱股票价格的稳定性.

[1]Gammaitoni L,Hänggi P,Jung P,Marchesoni F 1998Rev.Mod.Phys.70 223

[2]Mei D C,Du L C,Wang C J 2009J.Stat.Phys.137 625

[3]Du L C,Mei D C 2012Eur.Phys.J.B85 1

[4]Jia Y,Zheng X,Hu X,Li J 2001Phys.Rev.E63 293

[5]Zhang X Y,Xu W,Zhou B C 2011Acta Phys.Sin.60 060514(in Chinese)[张晓燕,徐伟,周丙常2011物理学报60 060514]

[6]Cao L,Wu D J 2007Europhys.Lett.61 593

[7]Shen C S,Zhang J Q,Chen H S 2007Acta Phys.Sin.56 6315(in Chinese)[申传胜,张季谦,陈含爽 2007物理学报56 6315]

[8]Spagnolo B,Valenti D,Fiasconaro A 2004Math.Biosci.Eng.1 185

[9]Valenti D,Fiasconaro A,Spagnolo B 2004Physica A331 477

[10]Bonanno G,Spagnolo B,Valenti D 2008Int.J.Bifurcat.Chaos18 2775

[11]Bonanno G,Spagnolo B 2005Fluct.Noise Lett.5 325

[13]Yoshimoto M,Shirahama H,Kurosawa S 2008J.Chem.Phys.129 014508

[14]Zeng C H,Zhang C,Zeng J K,Liu R F,Wang H 2015J.Stat.Mech.2015 08027

[15]Krawiecki A,Hołyst J A 2003Physica A317 597

[16]Babinec P 2002Chaos13 1767

[17]Li J C,Mei D C 2013Phys.Rev.E88 012811

[18]Bonanno G,Valenti D,Spagnolo B 2007Phys.Rev.E75 016106

[19]Bonanno G,Valenti D,Spagnolo B 2006Eur.Phys.J.B53 405

今年其他弟子运气并不好，也只余下他们三个来做第七试了，可为什么忽然改换到明天呢？太阳才刚刚偏西，离西北方向的终南诸峰尚远。三人百思不得其解，也只能辞别宇晴师父，回来小心准备。三人收了曲风送来的莲子，将宋歌生捞的白鱼去喂了小鲲，闷闷地晚饭，直到晚饭后被宇晴寻到，一路乘鲲来到这摘星楼上。

[20]Valenti D,Spagnolo B,Bonanno G 2007Physica A382 311

[21]Masoliver J,Perell J 2009Phys.Rev.E80 016108

[22]Masoliver J,Perell J 2008Phys.Rev.E78 056104

[23]Zhou W X 2007Introduction to Econophysics(Shanghai：Shanghai University of Finance&Economics Press)pp1-14(in Chinese)[周炜星 2007金融物理学导论 (上海：上海财经大学出版社)第1—14页]

[24]Yalama A,Celik S 2013Econ.Model.30 67

[25]Baaquie B E 1997J.Phys.I7 1733

[26]Angelovska J 2010VaR based on SMA,EWMA and GARCH(1,1)Volatility Models(Germany：VDM Verlag Dr.Müller)pp1-5

[27]Andersen T G,Tim B,Diebold F X,Paul L 2001Econometrica71 579

[28]Bouchaud J P,Potters M 2000Mpra.Paper285 18

[29]Gencay R,Dacorogna M,Muller U A,Pictet O,Olsen R 2001An Introduction to High-Frequency Finance(America：Academic Press)pp1-10

[30]Bollerslev T 1986J.Econom.31 307

[31]Ding Z,Granger C W J,Engle R F 1993J.Empir.Financ.1 83

[32]Bansal R,Kiku D,Shaliastovich I,Yaron A 2014J.Financ.69 2471

[33]Jebabli I,Arouri M,Teulon F 2014Energ.Econ.45 66[34]Heston S L 1993Rev.Financ.Stud.6 327

[35]Forde M,Jacquier A,Lee R 2012SIAM J.Financ.Math.3 690

[36]Drǎgulescu A A,Yakovenko V M 2002Quant.Financ.2 443

[37]Poon S H,Granger C W J 2003J.Econ.Literature41 478

[38]Fouque J P,Papanicolaou G,Sircar R,Solna K 2004Financ.Stoch.8 451

[39]Cox J C,Ingersoll Jr J E,Ross S A 1985Econometrica385

[40]Lux T,Marchesi M 2000IJTAF03 675

[41]Gopikrishnan P M,Martin Amaral,Nunes L,Stanley H E 1998Eur.Phys.J.B3 139

[42]Lillo F,Mantegna R N 2000Phys.Rev.E62 6126

PACS:05.40.—a,89.65.—s,02.50.—r DOI:10.7498/aps.66.040501

Influence of periodic volatility on the stability offinancial market∗

Zhou Ruo-Wei1)Li Jiang-Cheng1)2)†Dong Zhi-Wei1)Li Yun-Xian1)2)Qian Zhen-Wei1)
1)(Catastrophic Risk Management Research Center,School of Finance,Yunnan University of Finance and Economics,Kunming 650221,China)
2)(Department of Statistics,Yunnan University,Kunming 650091,China)

23 May 2016;revised manuscript

29 November 2016)

Various stochastic volatility models have been designed to model the variance of the asset price.Among these various models,the Heston model,as one-factor stochastic volatility mode,is the most popular and easiest to implement.Unfortunately,recent findings indicate that existing Heston modelis not able to characterize all aspects of asset returns,such as persistence,mean reverting,and clustering.Therefore,a modified Heston model is proposed in this paper.Compared with the original Heston model,the mean-reverting Cox Ingersoll and Ross process is modified to include a cosine term with the intention of capturing the periodicity of volatility.The phenomenon that high-volatile period is interchanged with low-volatile periods can thus be better described by adding such a period term to the volatility process.In addition,the geometric Brownian motion is replaced by a random walk in the presence of a cubic nonlinearity proposed by Bonanno et al.By doing so,a financial market with two different dynamical regimes(normal activity and extreme days)can be modeled.Closed-form solution for the modified Heston model is not derived in this paper.Instead,Monte-Carlo simulation is used to generate the probability density function of log-return which is then compared with the historical probability density function of stock return.Parameters are adjusted and estimated so that the square errors can be minimized.Daily returns of all the component stocks of Dow-Jones industrial index for the period from 3 September 2007 to 31 December 2008 are used to test the proposed model,and the experimental results demonstrate that the proposed model works very well.The mean escape time and mean periodic escape rate of the proposed modified Heston model with periodic stochastic volatility are studied in this paper with two different dynamical regimes likefinancial markets in normal activity and extreme days.Also the theoretical results of mean escape time and mean periodic escape rate can be calculated by numerical simulation.The experimental results demonstrate that 1)larger value of rate of return,smaller long run average of variance and smaller magnitude of periodic volatility will reduce the mean periodic escape rate,and thus stabilize the market;2)by analyzing the mean escape time,an optimal value can be identified for the magnitude of periodic volatility which will maximize the mean escape time and again stabilize the market.In addition,an optimal rate of relaxation to long-time variance,smaller frequency of the periodic volatility,larger rate of return,and stronger correlation between noises will furtherreduce the mean escape time and enhance the market stability.

periodic volatility,mean escape time,escape rate,econophysics

:05.40.—a,89.65.—s,02.50.—r

10.7498/aps.66.040501

∗国家杰出青年科学基金(批准号：11225103)、国家自然科学基金(批准号：11165016,71263056)、第57批中国博士后科学基金项目(批准号：2015M572507)和云南省博士后定向培养项目(批准号：C6153005)资助的课题.

†通信作者.E-mail：lijiangch@163.com

*Project supported by the National Science Fund for Distinguished Young Scholars of China(Grant No.11225103),the National Natural Science Foundation of China(Grant Nos.11165016,71263056),the China Postdoctoral Science Foundation(Grant No.2015M572507),and Postdoctoral Directional Ttraining Project in Yunnan Province,China(Grant No.C6153005).

†Corresponding author.E-mail：lijiangch@163.com