考虑出行行为的地铁公交网络优化*

田晟 许凯 马美娜

(华南理工大学 土木与交通学院， 广东 广州 510640)

考虑出行行为的地铁公交网络优化*

田晟 许凯 马美娜

(华南理工大学 土木与交通学院， 广东 广州 510640)

为研究新建地铁开通后配套公交线路的调整，从出行行为角度出发对地铁公交网络进行优化调整.引入前景理论描述有限理性出行者的路线选择行为，假定出行者总是追逐出行收益前景值最大，以此为目标建立路线选择模型.通过测试网络对前景理论和效用理论下的路网平衡态进行分析，结果显示：各路线流量在前景理论下达到平衡态的时间多于在效用理论下达到平衡态的时间，且前者存在较明显的流量振荡；前景值改变阈值对平衡态流量的影响体现了出行者对不确定性的风险抵抗，更贴合实际情况，可依此确定最终的公交线路.

地铁公交网络；出行行为；前景理论；路线选择

城市化进程吸引人口向大城市进一步转移，居民的出行需求随之上升.地铁因速度快、运量大、可靠性高等优势被各大城市积极采用，成为缓解出行压力、解决交通拥堵的有效途径.地铁线路的铺设需结合自然地形、出行量及TOD(公交引导发展)城市规划等确定；公交(指常规公交)在地铁沿线主要发挥其接驳作用，以扩大地铁作为城市交通骨干的辐射范围，公交因其线路可变性需在地铁开通后进行调整，以满足出行者对于公共交通的需求.文中拟探讨在地铁线路开通后与地铁相关的公交线路调整，从而为城市交通规划提供理论依据.

已有文献对地铁公交线网调整做了相关研究[1- 9].较普遍的是考虑网络的拓扑结构，通过调整公交线路对地铁公交网络系统优化，以提高地铁公交网络可达性，并以一个或多个指标作为优化的目标，另一些学者着重研究线路调整算法，比较不同启发式或智能算法对提高地铁公交系统网络性能的作用.如邓连波、范海雁、Amiripour等[1- 3]研究了车站站距、非直线约束等线网结构内容，从拓扑角度进行优化；Yan、Bagloee、 Mandl等[4- 6]以总成本最小或行程时间最小作为优化目标，以此进行线网调整；Xu、Cipriani、Mauttone等[7- 9]采用k最短路算法或改进遗传算法对目标值迭代求值，为路网优化算法提供参考.以上研究多以地铁公交网络系统为对象，以系统最优作为优化目标，忽略了从出行行为的角度考虑优化，或考虑了出行行为，但假定出行者对信息完全掌握，即完全理性出行者，而实际情况中，出行者了解信息有限，且存在习惯依赖性，调整过程需考虑出行者的有限理性.

文中在相关研究[10]的基础上，从出行行为角度对地铁公交网络进行设计优化，考虑在不确定和不完全信息条件下出行者的决策行为，引入前景理论描述出行者择路机制，出行决策行为体现在有限理性阈值的设定上，建立追逐出行收益前景值最大的路线选择模型，分析了出行者在路线上的流量转移，以流量最集中的线路作为地铁公交网络调整的优化线路.

1 地铁公交网络出行行为分析

1.1 出行行为分析

地铁公交网络的优化设计是以地铁的线路走向为基础，通过公交线路的调整设计，发挥其接驳作用来扩大地铁的辐射范围，提高网络可达性，且避免地铁公交网络的内部竞争.基于出行行为的线路调整贴合出行者的出行习惯，并从公交备选线路集中得出优化线路.

起讫点间的行程时间和总票价是出行者做出择路决策的两个主要因素，且出行者在出行过程中对换乘次数容忍度有限，一般不会超过2次，也不会选择公交-地铁-公交的复杂换乘形式.地铁线路开通后，有限理性条件下，出行者追逐出行前景值最大，根据前一天的出行经验更新当天出行路线的前景值，做出择路决策.

1.2 基于前景理论的出行选择行为

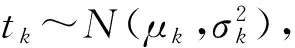
(1)

(2)

(3)

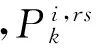
(4)

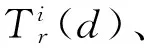
行程时间价值函数:

(5)

票价价值函数:

(6)

换乘次数价值函数:

(7)

总价值函数:

(8)

(9)

(10)

2 出行路线选择模型

出行者根据收益前景值在地铁公交网络中选择合适的出行路线，路线选择结果宏观上呈现了交通流量在路线间的分布状况，因此采用流量在各路线间的分布来表征出行路线选择结果.有限理性出行者的路线选择行为总是追逐路线收益前景值最大，根据式(10)计算的路线前景值，当不同路线间的前景值差值达到一定阈值时，出行者的出行路线改变，由前景值小的路线转向前景值大的路线.地铁公交网络优化设计时，有限理性出行者基于前景值在备选路线中选择出行路线，当天的路线选择依赖于前一天的出行结果.为描述路线选择情况，并选出地铁公交网络的优化线路，根据文献[15- 16]，建立基于前一天的出行路线选择模型，见式(11)-(13).

froute(d+1)=froute(d)+H(froute(d))

(11)

ξEPk1(d),0)fk1(d)Δk1k2

(12)

sum(H(froute(d)))=0

(13)

froute(d)是出行路线选择结果，表示第d天各路线流量分布；H(froute(d))表示有限理性出行者根据第d天出行经验在第d+1天出行的路线流量转移值；δ表示出行者路线改变系数；ξ表示考虑出行者习惯依赖性的前景值改变阈值，即可接受度，其值大于1，可接受度越高，流量在路线间的转移越小；fk1表示路线k1的流量；froute(d)、H(froute(d))及Δk1k2均为列向量，且维度为出行路线数n；Δk1k2表示k1和k2路线间的出行关联向量，其第k1行取(-1)，第k2行取1，其余值取0，k1、k2对所有出行路线取值.为研究出行者在地铁公交网络中的路线选择，需假定在研究时段内每日的出行量相等，sum函数表示对H(froute(d))所有列元素相加.

3 算例分析

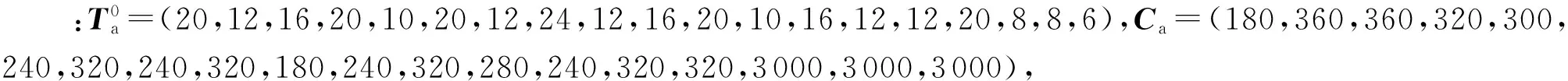
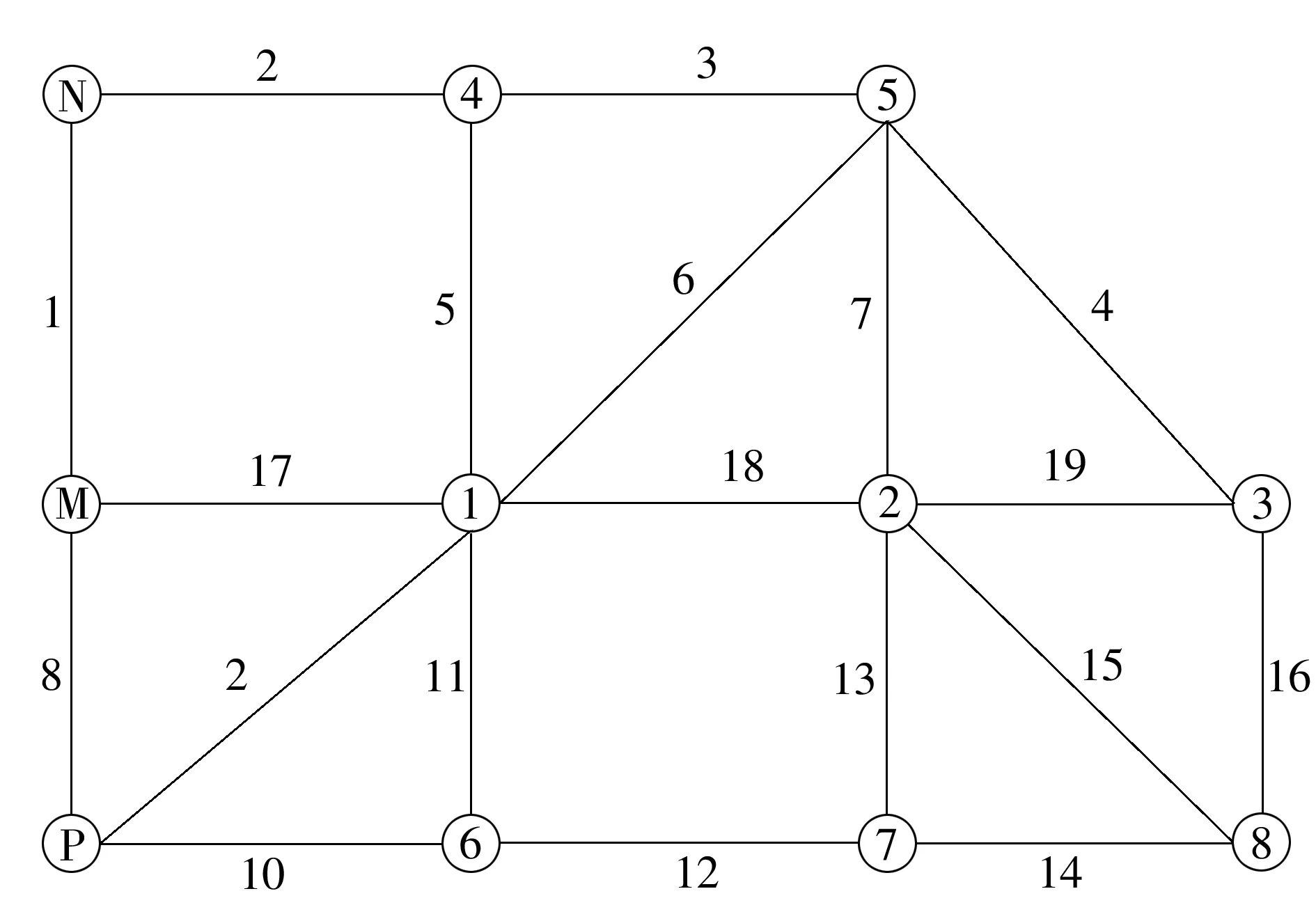
图1 地铁公交测试网络Fig.1 Metro bus test network

线路编号走向发车间隔/min0(地铁线)M-1-2-351N-4-1-6-7102P-1-5-32034-5-2-81046-7-8-310

根据地铁公交线路走向情况，有以下备选出行路线.路线a:N- 4-1-2-3(节点1换乘，1号线转0号线)，路线b：N- 4-1-5-3(节点1换乘，1号线转2号线)，路线c:N- 4-1-6-7-8-3(节点6或7换乘，1号线转4号线)，路线d:N- 4-5-3(节点4和节点5换乘，1号线转3号线转2号线).假定在地铁与公交间换乘时走行时间为10 min，公交与公交换乘时忽略走行时间，换乘等待时间为地铁公交发车间隔的一半，起讫点与起讫站点的平均走行时间为5 min，假定固定出发时刻为基准值0，要求准点到达时间为85 min，有限理性范围内允许早到及晚到时间分别为15 min和10 min，地铁每一站票价为2元，公交统一票价为2元，路线选择系统演化时间S=100 d.

图2和3分别是基于前景理论的每日路线流量演化图和基于效用理论的每日路线流量演化图.从图2看出，路线a在25 d时出现一明显拐点，产生该拐点的原因可能是该天之前路线a的前景值较大，出行者逐步向路线a转移导致阻抗值增加、前景值减小，该天之后前景值减小使得流量净流入为负，各路线流量在70 d左右收敛至平衡态.从图3可看出，与基于前景理论的择路模型相比，各路线流量波动较小，且未发生流量振荡现象，原因是在演化过程中流量在多条路线上呈梯度分布，而前者的流量在演化过程中出现集中于一条路线上的情况，路网呈非稳定态；基于效用理论的择路模型在20 d左右收敛至平衡态，体现了两模型择路机制的差异.

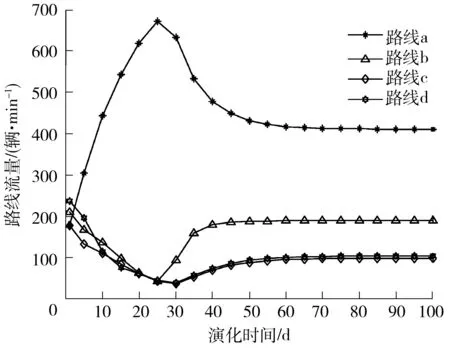
图2 基于前景理论的流量演化Fig.2 Flow evolution based on prospect theory

图3 基于效用理论的流量演化Fig.3 Flow evolution based on utility theory

表2是基于前景理论和效用理论的平衡态对比.可以看出，前景理论平衡态下的路线a、d流量高于效用理论平衡态，但前景理论平衡态下所有路线的行程时间均小于效用理论平衡态，原因是各路线间存在关联路段的相互作用，如路线a、b、c 3条路线有两路段重合，前景理论平衡态下，此3条路线的流量之和小于效用理论平衡态下的对应流量之和，故运用BPR函数计算路段阻抗值时，导致前者阻抗小于后者.前景理论平衡态下和效用理论平衡态下，按流量从大到小依次排序的路线分别是a-b-d-c和b-a-c-d，且前者路线流量下降速度逐步减慢，而后者下降速度逐步加快，原因是不同模型择路机制的差异.

表2 基于前景理论和效用理论的平衡态对比

Table 2 Comparison of equilibrium states based on prospect theory and utility theory

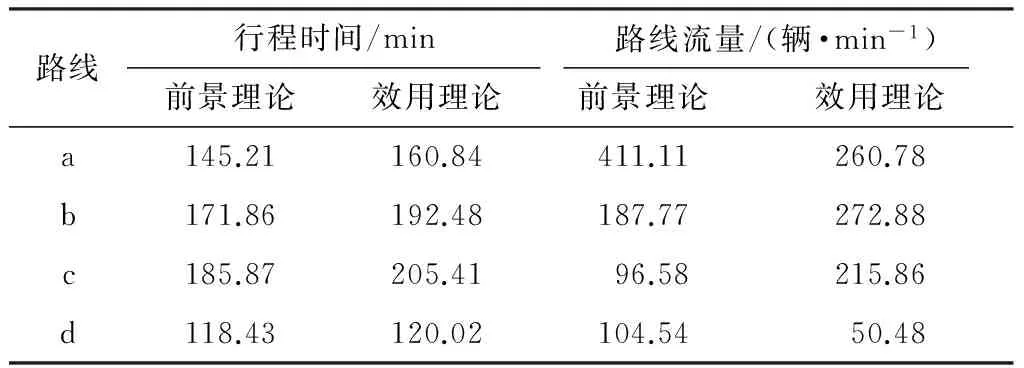
路线行程时间/min路线流量/(辆·min-1)前景理论效用理论前景理论效用理论a145.21160.84411.11260.78b171.86192.48187.77272.88c185.87205.4196.58215.86d118.43120.02104.5450.48

图4是各路线平衡态流量随可接受度ξ的变化情况.可以看出，随着ξ的增大，各路线流量值逐渐向平均值靠拢，各路线间的流量差别减小，原因是可接受度增加，演化过程中从前景值较小路线转向较大路线的出行者数量减少，体现了出行者的习惯依赖性对路线选择的影响及出行者对出行路线改变的风险抵抗.

图4 路线平衡态流量随可接受度的变化

Fig.4 Changes of equilibrium flow of route with acceptability

图5是各路线平衡态流量随站点2换乘公交等待时间的变化情况.考虑高峰期拥堵严重，地铁的换乘等待时间较为固定，而公交到站准点率较低造成换乘时间不确定的情况，此处选择路线b的换乘站点2对各路线平衡流量随该站点换乘公交时间的变化进行分析.可以看出，换乘时间在12 min以下时，各路线平衡态流量稳定，路线b的平衡流量未随换乘时间减少而增加，原因是在换乘时间小于换乘预期值时，出行者仍以预期值作为参考，体现出行者对换乘时间不确定性的风险抵抗；超过12 min后，各路线平衡态流量随等待时间增大向路线a进一步转移，路线a的流量在[20，27] min时段内发生明显变化，表明引起出行者路线转移的换乘时间阈值在该时段内；换乘时间超过27 min后，各路线平衡态流量在小范围振荡的值附近达到稳定，未向路线a继续集中，原因是换乘时间超过该值后，对换乘时间敏感的出行者已经完成了路线转移过程，其他路线上存在的流量体现了出行者路线选择过程中的随机性；路线c、d的换乘等待时间并未变化，但其流量变化与路线b具有类似的趋势，原因可能是在高峰时期，出行者会根据路网中已存在的拥堵情况进行预测并做出出行决策，选择换乘时间可靠性较高的路线，结果表现为流量向路线a转移.

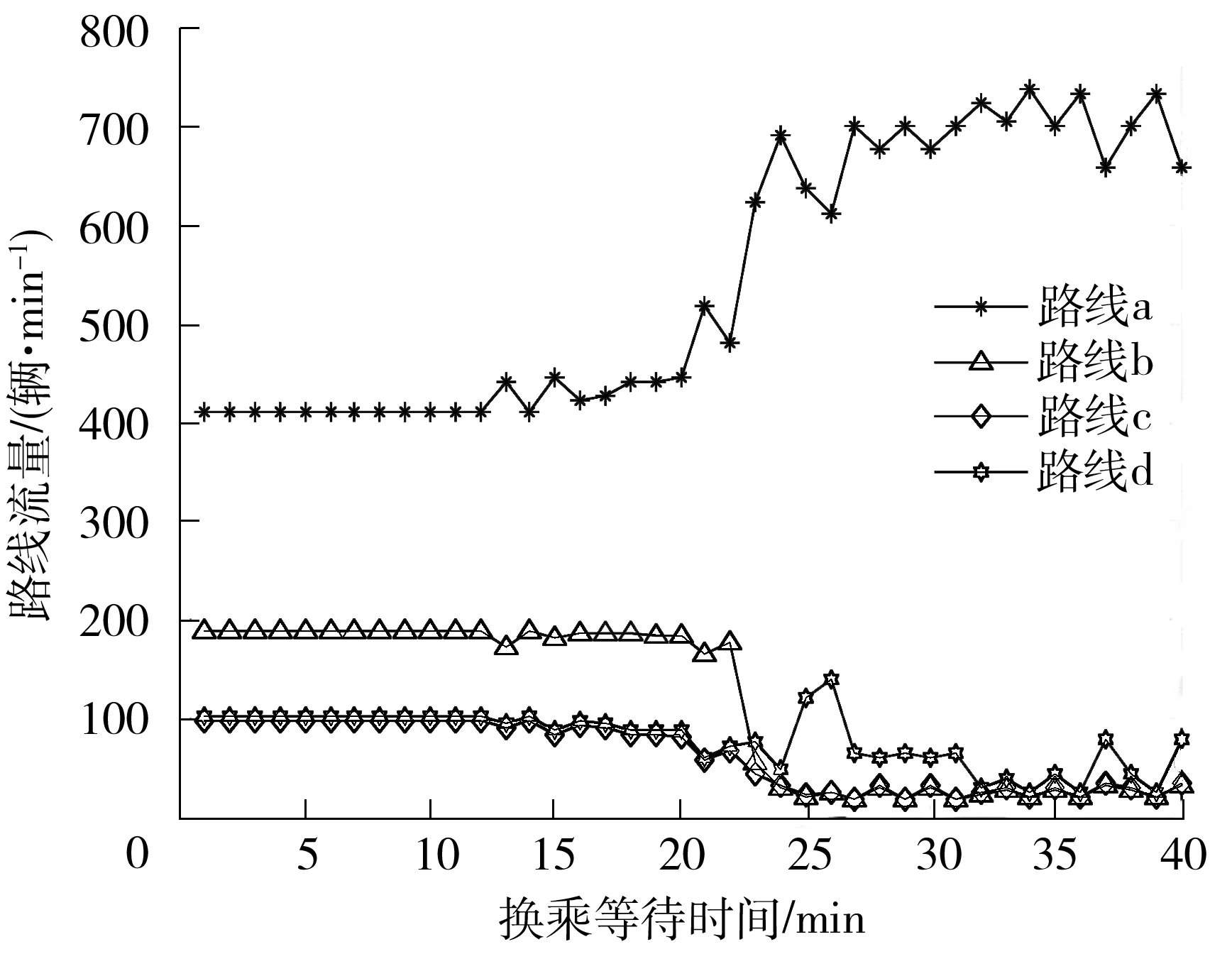
图5 路线平衡态流量随站点2换乘公交等待时间的变化

Fig.5 Changes of equilibrium flow of route with station 2 transfer bus waiting time

从考察OD对中选出流量分布最集中的路线，根据其地铁公交线路组成，确定线网优化的最终路线.基于前景理论平衡态的流量最大路线为路线a，即由1号公交线转0号地铁线，该路线平衡态流量较大，超过1/2的OD量，且拐点前线路a流量演变趋于总OD量，可采取减小路线阻抗值，如增大1号公交线路的发车频率.基于效用理论平衡态的流量最大路线为路线b，即由1号公交线转2号公交线，可以看出，其平衡态流量约为总OD量的1/3，且流量最大路线与次大路线差值较小，无明显优势.路线a较路线b行程时间短、票价高，基于前景理论的出行者愿支付更高票价以获得较短的行程时间，这更符合实际情况下的出行者心理，体现出行者追求行程时间最短的特点，故选择1号公交线作为地铁公交网络的最优线路.

4 结语

文中从出行行为角度对地铁影响下的公交线路进行调整优化.采用前景理论描述出行者在不确定和不完全信息条件下的出行选择行为，为抵抗出行过程随机性，出行者对地铁公交网络备选路线的行程时间、票价和换乘次数设置相应的参考点，在出行者追逐出行收益前景值最大的条件下，建立逐日演化的出行路线选择模型.最后通过一个简单的地铁公交测试网络验证了出行路线选择模型的作用，比较了基于前景理论和基于效用理论择路模型的差异，探讨可接受度对平衡态路线流量的影响,分析换乘时间对平衡态路线流量的作用，确定了优化线路.下一步的工作将是在前景值计算中纳入更多的因素，以更加真实地反应出行者心理，同时结合模型中参数的标定，对地铁公交线路进行调整优化.

[1] 邓连波,高伟,赖天珍,等.基于换乘网络的城市轨道交通关联公交接驳线网优化 [J].铁道科学与工程学报,2012,9(6):77- 83. DENG Lian-bo,GAO Wei,LAI Tian-zhen,et al.Optimal design of feeder-bus network related to urban rail transit based on transfer network [J].Journal of Railway Science and Engineering,2012,9(6):77- 83.

[2] 范海雁,杨晓光,夏晓梅,等.基于轨道交通的常规公交网络调整方法 [J].城市轨道交通研究,2005(4):36- 38. FAN Hai-yan,YANG Xiao-guang,XIA Xiao-mei,et al.Bus line networks adjustment on rail transit basis [J].Urban Mass Transit,2005(4):36- 38.

[3] AMIRIPOUR S M M,MOHAYMANY A S,CEDER A.Optimal modification of urban bus network routes using a genetic algorithm [J].Journal of Transportation Engineering,2015,141(3):04014081.

[4] YAN Y,LIU Z,MENG Q,et al.Robust optimization model of bus transit network design with stochastic travel time [J].Journal of Transportation Engineering,2013,139(6):625- 634.

[5] BAGLOEE S A,CEDER A.Transit-network design me-thodology for actual-size road networks [J].Transportation Research Part B Methodological,2011,45(10):1787- 1804.

[6] MANDL C E.Evaluation and optimization of urban public transportation networks [J].European Journal of Operational Research,1980,5(6):396- 404.

[7] XU W,HE S,SONG R,et al.Finding the K shortest paths in a schedule-based transit network [J].Computers & Operations Research,2012,39(8):1812- 1826.

[8] CIPRIANI E,GORI S,PETRELLI M.Transit network design:a procedure and an application to a large urban area [J].Transportation Research Part C Emerging Technologies,2012,20(1):3- 14.

[9] MAUTTONE A,URQUHART M E.A route set construction algorithm for the transit network design problem [J].Computers & Operations Research,2009,36(8):2440- 2449.

[10] JENSEN A F.Bounded rational choice behaviour:applications in transport [J].Transport Reviews,2016,36(5):680- 681.

[11] 康拥政.基于居民出行需求的公交线网优化模型研究 [J].铁道运输与经济,2006,28(9):45- 46. KANG Yong-zheng.Study on the optimization model of public transport network based on the demand of resident trip [J].Railway Transport and Economy,2006,28(9):45- 46.

[12] MAHMASSANI H S,LIU Y H.Dynamics of commuting decision behaviour under advanced traveller information systems [J].Transportation Research Part C Emerging Technologies,1999,7(2):91- 107.

[13] SHEFFI Y.Urban transportation networks:Equilibrium analysis with mathematical programming methods [M].Englewood Cliffs,NJ:Prentice Hall,1985.

[14] TVERSKY A,KAHNEMAN D.Advances in prospect theory:cumulative representation of uncertainty [J].Journal of Risk & Uncertainty,1992,5(4):297- 323.

[15] SMITH M,HAZELTON M L,HONG K L,et al.The long term behaviour of day-to-day traffic assignment models [J].Transportmetrica A Transport Science,2014,10(7):647- 660.

[16] SMITH M J.The stability of a dynamic model of traffic assignment:an application of a method of Lyapunov [J].Transportation Science,1984,18(3):245- 252.

Optimization of Metro and Bus Network Considering Travel Behaviors

TIAN Sheng XU Kai MA Mei-na

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China)

In order to effectively adjust the supporting bus lines after the opening of a new subway line, an optimization of metro and bus network is made from the viewpoint of travel behavior. By introducing the prospect theory to describe the behaviors of bounded rational travelers and by assuming that travelers always chase the maximum value of foreground, a model for route selection is set up. Moreover, the equilibrium state of the road network under the prospect theory and the utility theory is analyzed by testing the network. The results show that the time of equilibrium state under the prospect theory is longer than that under the utility theory, and that the former shows obvious flow oscillation. In addition, the influence of the change threshold of foreground value on the equilibrium flow reflects the risk resistance of travelers to uncertainty, so that it is more suitable for the real situation and more effective in determining the final bus line.

subway and bus network; travel behavior; prospect theory; route selection

2016- 10- 31

国家自然科学基金资助项目(61174188)；华南理工大学百步梯攀登计划项目(GB30317028) Foundation item: Supported by the National Natural Science Foundation of China(61174188)

田晟(1969-)，男，博士，副教授，主要从事交通运输工程等的研究.E-mail:shitian1@scut.edu.cn

1000- 565X(2017)06- 0031- 06

U 491

10.3969/j.issn.1000-565X.2017.06.006