M EM S陀螺静态误差补偿方法研究
付建立
(中航航空电子有限公司,北京100098)
M EM S陀螺静态误差补偿方法研究
付建立
(中航航空电子有限公司,北京100098)
针对典型MEMS陀螺静态误差大、影响工程上使用的难题,提出基于时间序列模型的Kalman滤波方法。通过对典型MEMS陀螺数据进行分析,提取其趋势项,进行周期检验与相关性分析,建立时间序列模型;针对建立的时间序列模型,提出利用Kalman滤波方法,消除零位不稳定性。仿真及试验结果表明,该解算方法能够有效补偿MEMS陀螺静态误差,显著提升其静态指标。
误差补偿;静态误差;Kalman滤波;零位不稳定性
Abstract:In view of the large static error of typicalMEMSgyroscope and the difficult problem in engineering,a Kal⁃man filteringmethod based on time seriesmodel is proposed.Based on the typical MEMS gyro data analysis,extraction of the trend analysis,periodic inspection and correlation,time seriesmodel is established.According to the time sequence model,proposed using Kalman filteringmethod to eliminate the zero stability.Simulation and experimental results show that the proposed method can effectively compensate the static error of MEMSgyro and improve its static index significantly.
Key w ords:error compensation;static error;Kalman filtering;zero instability
0 引言
MEMS概念的首议者、美国著名物理学家Fey⁃man曾经指出,MEMS技术发展的一个问题就是如何用低精度工具制造高精度产品。对MEMS惯性器件进行误差补偿是提高其精度的一个重要手段,因此,很多MEMS技术领先的研究机构将研究的重点转型MEMS陀螺结构误差建模和误差补偿方法的研究,以提高陀螺的性能和鲁棒性。
在补偿 MEMS惯性器件或惯性测量单元(IMU)误差时,诸如零偏、零偏不稳定性、标度因数误差、失准角和随机噪声等,需要建立起其误差模型和进行模型参数辨识,然后实施补偿。误差模型可以分为静态误差模型、动态误差模型和随机误差模型。对于静态误差模型和动态误差模型一般认为是与载体运动的速度、加速度等有关的确定性误差项,可通过试验标定并补偿。对于零位不稳定性误差模型,只能采用合理的模型辨识和参数估计方法。
陀螺零位不稳定性是陀螺仪的重要特性,国内外在陀螺漂移测试及建模方面做了大量工作。本文系统地分析了将时间序列方法应用于MEMS误差补偿中的整个过程,为误差补偿与分析提供了理论支撑。
1 陀螺零位不稳定性误差的时间序列分析与建模
时间序列是一种时域分析方法,它不仅研究过程的确定性变化,更注重过程随机性变化。它直接用随机时间序列建立差分方程,将一个高度相关的平稳时间序列表示为一种数字递推的形式,即认为是由各时刻相关的随机时间序列和各时刻出现的白噪声组成。时间序列的建模就是对时间序列 {xk}(k=1,2,…,M)拟合出适用的模型。建模的内容包括数据采集、数据统计检验和预处理、模型形式的选取、模型参数的估计和模型实用性的检验 (确定模型的阶次)[1]。
2 陀螺输出数据预处理
为了获取足够多的陀螺漂移数据作为样本,对所研究的MEMS陀螺进行了长时间的测试。为保证测量的精度,陀螺被安放在转台上,并保持室温稳定。采集陀螺上电后1h数据,采样频率为100Hz,室温为25℃,并对输出数据进行10阶滑动平均处理,所得到的陀螺漂移数据如图1所示。
从图1可知,该陀螺的漂移数据为非平稳时间序列,因此建模前需要进行统计检验以及相关的预处理。在分析过程中,采用轮次法进行平稳性检验。
2.1 漂移数据趋势项的提取与剔除
具有趋势项的非平稳随机信号xt是由确定性部分dt和平稳随机部分st所组成,即:
趋势项dt可以为线性函数、幂函数、指数函数即周期函数等,采用线性趋势项提取法,不断提高多项式阶次,并对去除趋势项的残差进行平稳性检验,不采用差分方式。陀螺漂移的二次拟合曲线,如图2所示。
采用轮次检验法对去除趋势项后的陀螺输出进行平稳性检验,结果如表1所示。
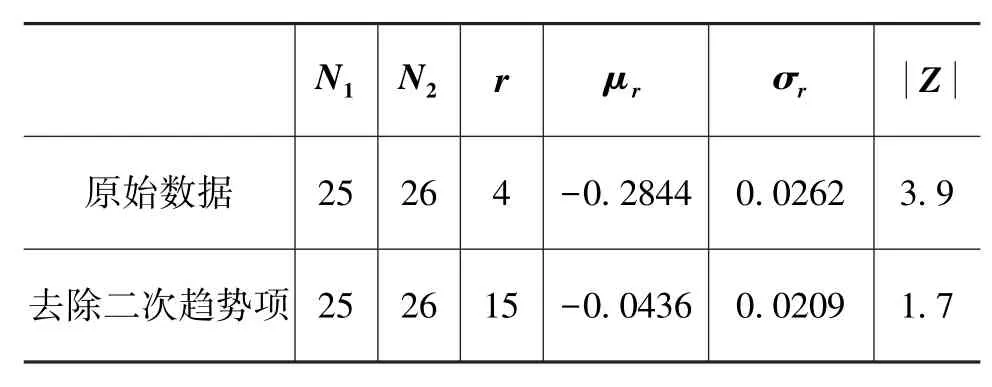
表1 陀螺漂移轮次法检验参数表Table 1 Test parameters of gyro drift turn method
2.2 周期性检验
周期性检验用来识别陀螺零位不稳定性数据中是否包含有随机量以外的周期性分量,周期性检验的方法是直接考察从漂移数据得到的概率密度函数、自相关函数或功率谱密度的图形。对去除趋势项的陀螺漂移进行了周期性检验,其功率谱密度图形如图3所示。由图3可知,陀螺漂移数据的能量集中在低频区,无周期性成分。
2.3 自相关与偏相关函数
对于不同系统产生的随机序列,可能采用不同的模型来描述。而这几类模型之间存在着差别,ARMA模型、AR模型和MA模型之间的差别在它们的自相关函数和偏自相关函数上会反应出不同的特性,具体如表2所示。
所谓拖尾,是指它随着k增大,以负指数的速度趋向于0,此时它的图像就像拖着一条尾巴;所谓截尾,是指它的图像像截断了尾巴一样,而断尾处在k=p的地方[2]。
因此,样本序列自相关函数ρ^k和偏相关函数φ^kk的分析可用来判断该随机序列属于何种类型的模型。
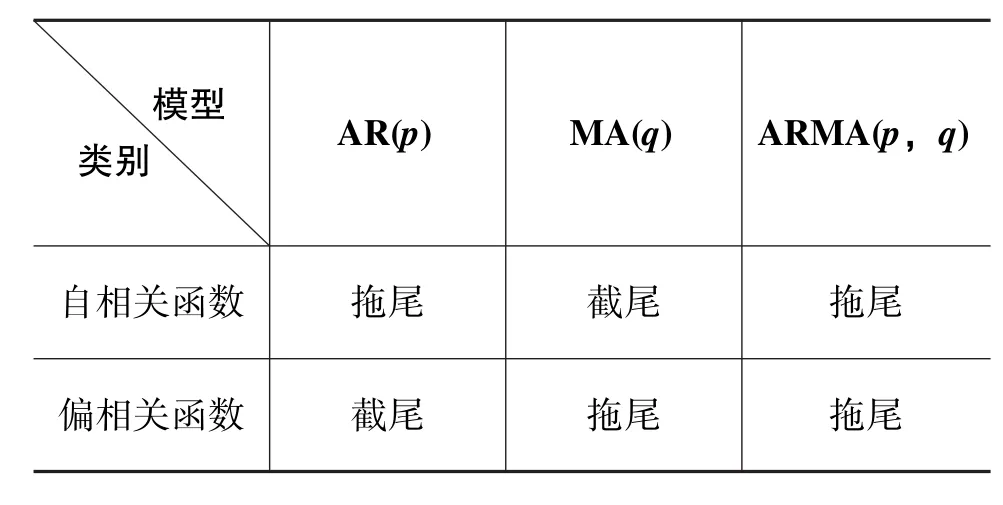
表2 模型自相关函数、偏相关函数关系Table 2 Model relationship between autocorrelation function and partial correlation function
由于样本序列自相关函数ρ^k和偏相关函数φ^kk的截尾或拖尾是用作识别平稳随机序列模型的依据,为此,列出它们的计算式如下[3]:
自相关函数估计式为:
其中,
式中,xi为ti时刻陀螺漂移数据,xi+k为ti+k时刻陀螺漂移数据,k为滞后数,k=1,2,…,m(m≤N),m为最大滞后数。偏相关函数估计式为:
式中, φ^kj=φ^k-1,j-φ^kkφ^k-1,k-j(j=1, 2, …, k-1)。
从图4、图5可知,自相关函数示意图存在拖尾现象,偏相关函数示意图存在截尾现象。根据表2,与图4、图5中对应的模型为AR(p)模型,得到的自相关和偏相关函数如图6、图7所示。
综上所述,应重点考察AR(p)模型,除上述理论推导外,阶数越少,在硬件实现上越方便。
3 模型选取及参数估计
通过数据预处理,对基本模型进行识别后,就可以对模型参数进行估计。对陀螺漂移据,通常采用AR(p)、ARMA(p,q)模型来拟合,模型参数的估计就是估计它们的参数 φ1、 φ、 …、 φp、θ1、θ2、…、θq以及白噪声方差 σ2a, 由漂移数据自相关函数即偏相关函数可以判断其漂移模型为[6]:
写出与其相应的Kalman滤波方程的状态空间模型。
其中,V(k)、W(k)的统计特性为:
从系统的观点出发,可以认为陀螺漂移是以白噪声为输入的系统输出。设系统的状态向量:X(k)=[xkxk-1]T; 过程噪声为:W(k)=[wkwk-1]T,量测噪声为:V(k)= [vk0]T。状态方程中的相关系数为:
对上述系统方程,Kalman滤波递推方程为[6]:
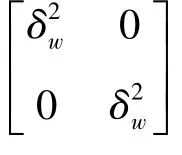
4 试验验证
利用上述方法,对MEMS器件进行补偿试验。共试验6次,具体如表3~表6所示。
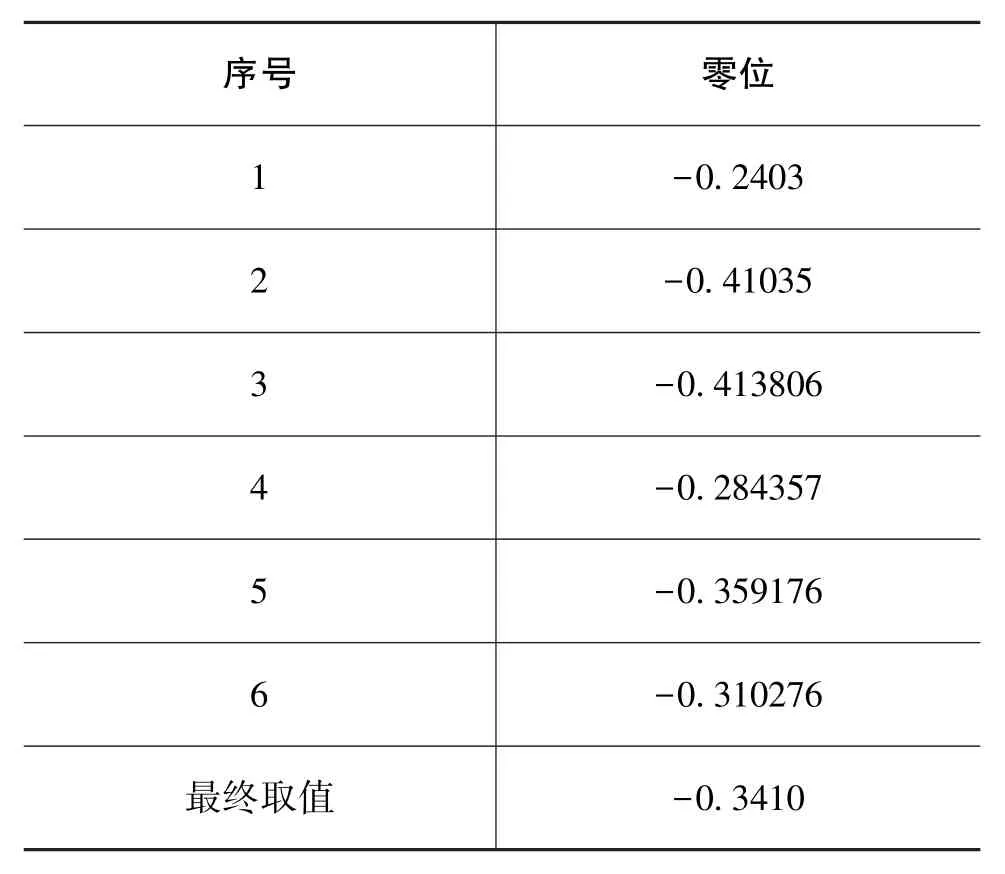
表3 试验数据Table 3 Data of the test
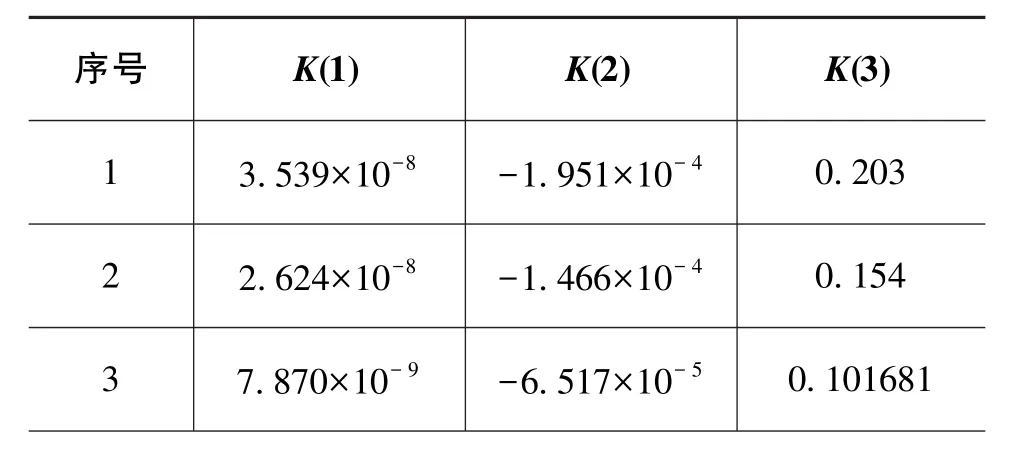
表4 趋势项拟合值Table 4 Trend fitting value
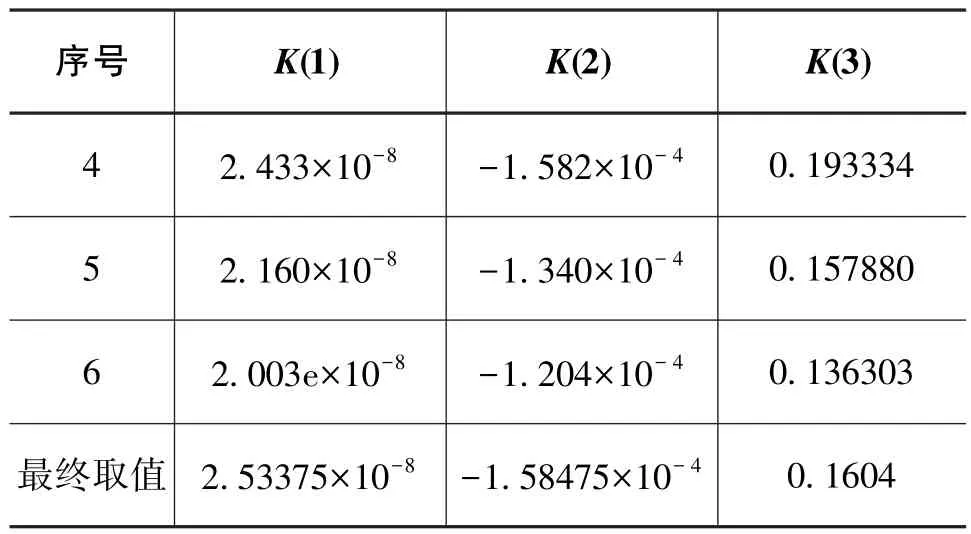
续表

表5 AR(1)模型取值Table 5 Value of AR(1)model
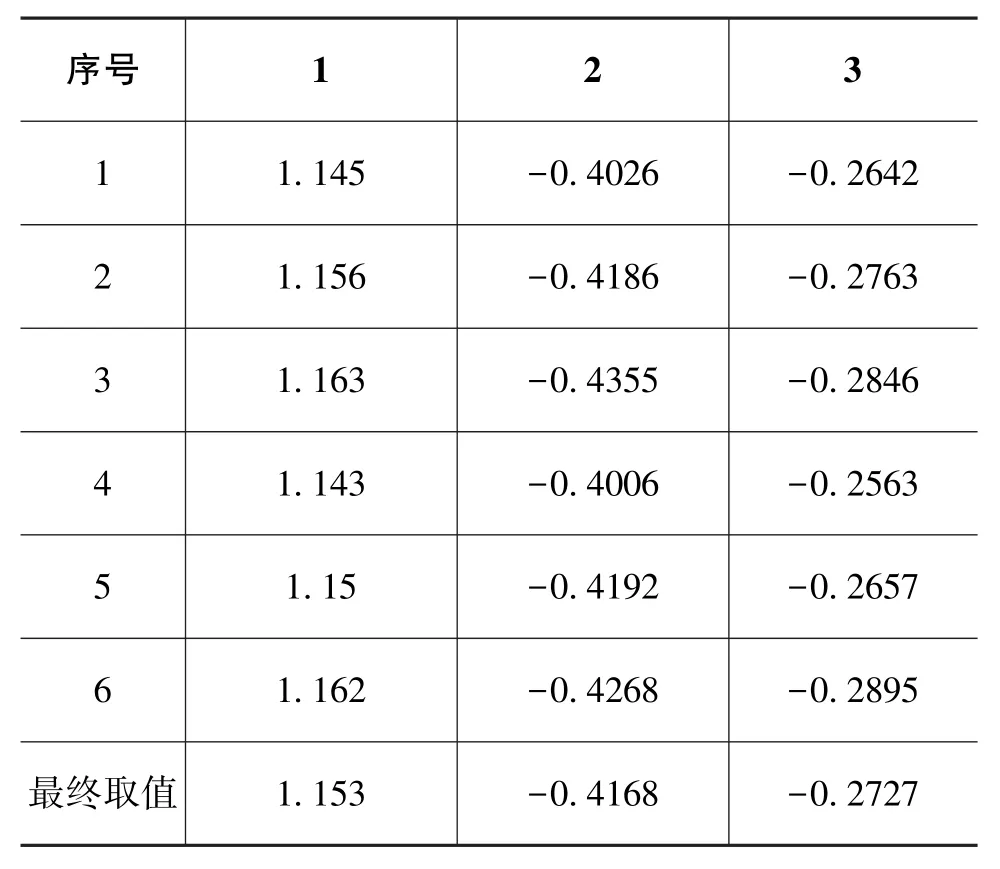
表6 ARMA(2,1)模型取值Table 6 Value of ARMA(2,1)model
AR(1)模型与ARMA(2,1)模型相比,相差不大,故在硬件实现上,选择AR(1)模型作为滤波模型。
对上述模型进行验证,结果如图8所示。
利用Allan方差法对陀螺数据进行分析,结果如图9所示。
根据图9分析结果,可计算得陀螺的零偏稳定性为9.3347(°)/h,角度随机游走为1.4875(°)/h1/2。
5 结论
针对典型MEMS陀螺静态误差大、影响工程上使用的难题,提出基于时间序列模型的Kalman滤波方法。通过对典型MEMS陀螺数据进行分析,提取其趋势项,进行周期检验与相关性分析,建立时间序列模型;针对建立的时间序列模型,提出利用Kalman滤波方法,消除零位不稳定性。仿真及试验结果表明,该解算方法能够有效补偿MEMS陀螺静态误差,显著提升其静态指标。
[1]IEEE 1431⁃2004,IEEE standard specification format guide and test procedure for coriolis vibratory gyros[S].New York:Institute of Electrical and Electronics Engineers,2014.
[2]严恭敏,李四海,秦永元.惯性仪器测试与数据分析[M].北京:国防工业出版社,2012.YAN Gong⁃min,LI Si⁃hai,QIN Yong⁃yuan.Inertial in⁃strument test and data analysis[M].Beijing:National De⁃fense Industry Press,2012.
[3]何昆鹏.MEMS惯性器件参数辨识及系统误差补偿技术[D].哈尔滨工程大学,2009.HE Kun⁃peng.Parameter identification and system error compensation technique of MEMS inertial device[D].Harbin Engineering University,2009.
[4]尹文.MIMU微惯性测量单元误差建模与补偿技术[D].国防科学技术大学,2007.YIN Wen.Error modeling and compensation technique of MIMU micro inertialmeasurement unit[D].National Uni⁃versity of Defense Technology,2007.
[5]毛奔,林玉荣.惯性器件测试与建模[M].哈尔滨:哈尔滨工程大学出版社,2008.MAO Ben,LIN Yu⁃rong.Inertial device testing andmodeling[M].Harbin:Harbin Engineering University Press,2008.
[6]陈良均,朱庆棠.随机过程及应用[M].北京:高等教育出版社,2003.CHEN Liang⁃jun,ZHU Qing⁃tang.Stochastic processes and applications[M].Beijing:Higher Education Press,2003.
Research on Static Error Com pensation M ethod of M EM S Gyroscope
FU Jian⁃li
(AVIC Avionics Co.,Ltd,Beijing 100098)
TP212.1
A
1674⁃5558(2017)02⁃01412
10.3969/j.issn.1674⁃5558.2017.04.009
付建立,男,计算机科学专业,研究方向为飞行器导航、飞行模拟及数据分析等。
2017⁃05⁃16

