由“聚”到“散”，提升核心运算能力——以苏教版六下“运算律和运算性质总复习”教学片段为例

董 良

由“聚”到“散”，提升核心运算能力
——以苏教版六下“运算律和运算性质总复习”教学片段为例

董 良

《义务教育数学课程标准（2011年版）》中将“运算能力”作为十大核心概念之一，强调理解运算的算理，并寻求合理简洁的运算途径解决问题。对于运算律和运算性质的总复习教学，需要通过对运算律、性质的“聚合”及在解决问题中“发散”运用，深入挖掘运算律、运算性质的本质特征及其相通之处，提升学生的核心运算能力。

小学数学；聚合；发散；运算能力

运算能力是 《义务教育数学课程标准（2011年版）》在修订过后增加的十个核心概念之一，也是作为三种基本数学能力之一（还包括空间想象能力和逻辑思维能力——林崇德语），对数学学习来说起到了基石性的作用。没有运算能力的支撑，不可能学好数学。《义务教育数学课程标准（2011年版）》也指出：“培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。”运算能力是运算技能与数学思维的结合，主要指能够根据概念、公式、法则、定理等对题目进行正确的运算，及在理解运算算理的基础上，能够借助数学思想方法，寻求合理的运算途径，并可以灵活地解决问题。

作为毕业阶段的计算总复习教学，如何在学生已有的六年计算技能的基础上，进一步做到理解运算的算理，正确地进行运算，同时在运算的过程中更加合理地运算、简洁地运算，笔者试以六年级下册“运算律和运算性质总复习”的教学片段为例，对复习课培养核心运算能力进行探讨。

一、聚——沟通联系，凸现运算律本质特征

这里的“聚”是将小学阶段所学过的各个运算定理和性质整合在一起，经过抽象整理，进行系统梳理，让学生能够深入地挖掘出运算定律、运算性质的本质特征及其相通之处，为接下来合理、灵活地通过运算解决问题找到充分的理论根据。

请看下面的教学片段：

师：我们都学过了哪些运算定律，你能用字母表示出来吗？

学生回答，教师根据学生的回答相机用磁性卡片贴出。

（图1）

师：看着这些字母表达式，你能试着说说它们分别表示什么意思吗？

先同桌讨论，再全班交流。

师：如果请你给它们分类，你准备怎样分？小组内讨论。

生：分成加法和乘法两大类。

师（根据学生的回答调整卡片的位置）：说说你的依据。

生：分成三类，交换律、结合律和分配律。

根据学生的回答重新调整卡片的位置。

（图2）

师：谁能说说看，交换律有什么特点？（变的是数的位置，不变的是计算结果。）

师在交换律的左边板书：位置改变。

师：结合律有什么特点？（变的是运算顺序，不变的是计算结果。）

师在结合律左边板书：运算顺序改变。

师：乘法分配律有什么特点？（变的是计算的方法，不变的是计算结果。）

师在分配律左边板书：计算方法改变。

（图3）

师：这里的计算方法怎么改变啦？

生：可以先求积，再求和；也可以先求两个不同乘数的和，再求积。

师：老师发现，同学们所说的运算律都是加法和乘法的，那减法和除法有没有呢？

生：减法和除法有运算性质。

师：谁能用字母表示减法和除法的运算性质？

生回答，师相机卡片贴出。

（图4）

师：看着字母表达式，能给大家解释一下吗？

生举例说明。

师：学了这么多的运算律和运算性质，你觉得最大的好处是什么呢？（使计算简便。）

板书：计算简便

师：为什么可以利用它们来进行简便计算呢？

生：因为用了运算律，只是计算的方法改变了，但是结果不变。

板书：结果不变。

（图5）

针对六年级的学生已经具备了一定的归纳整理能力这一特点，教师并没有简单地罗列各个知识点，而是引导学生通过观察、思考、交流，找出各部分内容之间的关系或蕴藏的规律，建立良好的认知结构。教师先让学生回忆学习过的运算定律，接着让学生试着将学过的运算定律进行分类，并说出这样分类的依据，寻找各自的特点，从而沟通各运算定律之间的联系，并由 “加法、乘法”引申到“减法、除法”，接着回顾整理运算性质，最后通过讨论、交流，学生总结得出结论：学习了运算定律和运算性质，可以在计算结果不变的情况下，使计算变得简便。从而将各个知识点连接起来，形成一个系统的，有联系的，有结构的知识网络。在这个过程中，教师给了学生足够的时间、空间，让学生创造性地完成知识结构与认知结构的构建。

二、散——拓展应用，提升核心运算能力

曹才翰先生在《中国中学教学百科全书（数学卷）》中指出，运算能力并非一种单一的数学能力，它是运算技能与逻辑思维能力的一种独特结合。学生运算能力的发展主要通过数学解题活动来实现。学生的运算能力主要表现为能正确、迅速的感知题目形式，确定题目类型，根据题目类型选择解题模式、解题方法，然后多方向地寻求解题方法，摆脱思维定式，力求解法简洁合理，并对题目类型、解题模式方法进行反思总结概括等。

经过前面的抽象整理，接下来则需要从练习设计中放大核心知识，才能体现知识的连贯性，经历抽象整理、拓展应用的过程，体现了复习课中对已学知识的“聚合”和在应用知识中“发散”的功能与特征。

接着看下面的练习教学片段：

第一关：仔细审题，怎样简便就怎样算。

师：我们在做题之前，一定要先看清题目的要求，谁来读一下这里的题目要求，要读得有水平！

师：你是怎么理解这个要求的？

生：就是要灵活选择合适的方法来计算。

师：那好，我们就按照这样的要求再来练几题。（出示课件）

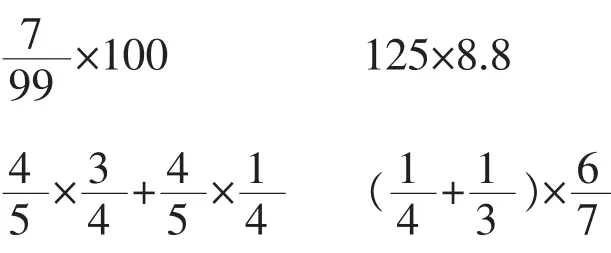
生在作业纸上完成，集体反馈。

师：这样做的举手？（少数学生举手，大多数学生对比屏幕后恍然大悟。）

师：是这样做的举手？（大部分学生无奈地举手）

师：觉得哪种方法更简便？

生：第一种。

课件出示：

师：有不同的做法吗？

学生答，课件出示：

师：有什么想说的吗？

生：125×8.8既可以用分配律，也可用结合律。

课件出示：

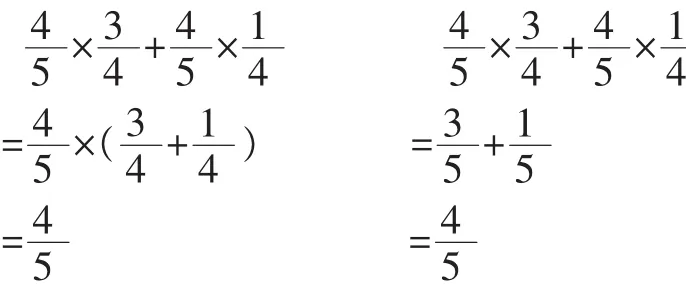
师：比较一下这一题的两种方法，发现什么？

生：既可以用分配律，也可以直接约分，先算乘法，再算加法。

课件出示：

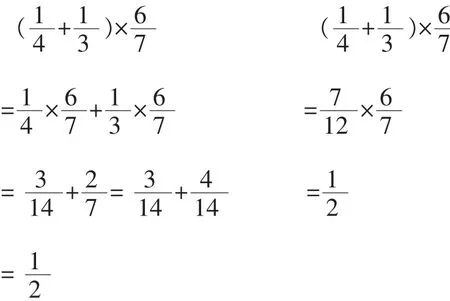
师：发现什么了？

生：用了乘法分配律，反而不简便了。

师：现在让我们再观察一下这4道题，有什么感想，想和大家交流？

生：我理解了什么是“怎样简便就怎样算”，我觉得做题的时候一定要根据实际情况选择合适的方法，有的时候不运用运算律，反而会更简便。

第二关：自己来编题，在括号里填数，运用运算律和运算性质让计算简便。

师：先独立思考，再在小组里交流。

解决问题时运算方法合理、简洁是运算能力较高的要求。但事实上，许多学生在运用运算律和运算性质时，往往流于僵化，主要体现在三点：（1）运用运算定律和运算性质计算时思维定式严重，常囿于一种思路和方法，不愿意思考是否可以运用多种运算定律或性质进行计算。（2）面对“能简便计算的要简便计算”时，学生能意识到要运用运算定律进行简便计算，面对其他情况下则无此意识。（3）对于“怎样简便就怎样算”，理解成了一定要运用各种运算定律和运算性质进行计算，不会灵活地选择计算方法。教师在这里的处理是独具匠心的，各种“陷阱”，学生屡屡中招，才能在计算、交流、辨析中提升对“怎样简便就怎样计算”的理解。不仅如此，教师还关注后续学习，拓展思维深度。让学生根据运算律和运算性质改编或自编习题。这样先“聚合”再“发散”的处理，体现了复习课中特别是毕业班复习教学的基本要求与策略，让学生的学习真实发生，真正提升了核心素养的运算能力。

当然，运算能力的培养与发展是一个长期的过程，应伴随数学知识的积累而淡化。运算能力的培养与发展不仅包括运算技能的逐步提高，还应包括思维素质的提升和发展，真正把 “运算能力”作为数学核心素养，就要从纯粹计算的外表进入到学生思维的核心，从教师的说教牵引向学生自我醒悟的核心，从能算、会算发展到合理的算、简洁的算的核心。这是运算教学的至高追求。

［1］汤卫红.基于核心素养的运算能力及其培养［J］.福建教育，2016（Z5）:96-99.

［2］陈文梅.数学核心素养之运算能力的培养［J］.小学数学教育，2016（Z3）：41-46.

G623.5

A

1005-6009（2017）49-0041-04

董良，苏州大学实验学校（苏州，215133）教师，高级教师，苏州市双十佳青年教师，苏州市小学数学兼职教研员。