基于电磁波反射和折射理论的平底孔试件脉冲涡流检测解析模型∗
张卿 武新军
(华中科技大学机械科学与工程学院,武汉 430074)(2016年7月8日收到;2016年10月26日收到修改稿)
基于电磁波反射和折射理论的平底孔试件脉冲涡流检测解析模型∗
张卿 武新军†
(华中科技大学机械科学与工程学院,武汉 430074)(2016年7月8日收到;2016年10月26日收到修改稿)
针对大多数脉冲涡流检测解析模型假设试件壁厚均匀减薄,其解析解中仅包含z方向(试件厚度)信息,不能求解探头覆盖区等依赖r方向(平行试件表面)信息的问题,本文提出平底孔试件脉冲涡流检测解析模型.该模型在z和r方向均存在介质分界面,边界条件复杂,求解困难.为此,本文首先假设平底孔所在层导体与空气区域的横向波数和纵向波数均相同,且横向波数为仅与r方向结构有关的实数,纵向波数为与该层横向波数和导体区域材料有关的复数,在此假设基础上应用电磁波反射和折射理论,构造各层波动方程;然后通过引入r方向结构系数Wn,将Cheng的矩阵法扩展,用扩展的矩阵法求解波动方程,得到模型的解析表达式.将该模型应用到16MnR平底孔试件检测实例中,并对其进行实验验证.模型计算结果与实验结果基本符合,证明了模型的正确性.平底孔试件脉冲涡流检测解析模型有助于加深对脉冲涡流检测结果的理解,同时能够为r方向逆问题求解提供理论依据.
脉冲涡流检测,反射与折射理论,平底孔,解析模型
1 引 言
压力容器、电站锅炉等由铁磁性材料制成的设备常用于石油、化工等行业[1−3],开展无损检测与评估是保障设备安全运行的重要手段.在众多的无损检测方法中,基于电磁感应原理的脉冲涡流检测技术因具有非接触性、穿透深度大、检测速度快等优点而得到广泛应用[4,5].
脉冲涡流检测技术采用方波或阶跃方式激励,通过分析接收线圈感应电压得到试件厚度、电导率等信息.解析模型能用显式表示感应电压与试件厚度、电导率等的关系,且计算速度快,物理意义明确,因此对脉冲涡流检测技术至关重要.
脉冲涡流检测解析模型的基础主要是Dodd-Deeds模型[6],然而,Dodd-Deeds模型的求解域为半无限大,因而其结果中包含Bessel函数二重积分项,计算困难.Theodoulidis和Kriezis[7,8]应用截断区域特征函数展开法(truncated region eigenfunction expansion,TREE),将无限大求解域缩小到一定半径的圆柱体,则Bessel函数二重积分转换为级数形式,简化了Dodd-Deeds模型的求解,扩大了解析模型的适用范围.随后,范孟豹等[9]应用TREE法和电磁波的反射与折射理论推导了多层导电结构涡流检测解析模型,简化了多层导电结构模型的求解,进一步扩大了模型的适用范围.
应用上述模型,脉冲涡流检测中的诸多问题得到了解决,如试件厚度、电导率等逆问题求解[10,11],提离效应的分析与抑制[12,13],激励参数对检测结果的影响分析[14]等.然而,上述模型假设试件均匀壁厚减薄,其感应电压表达式中仅包含试件厚度(即z方向)信息.近年来,随着脉冲涡流检测技术的快速发展,探头覆盖区[15,16]、边缘效应[17]、局部壁厚减薄缺陷定量[18]等问题的研究越来越受到重视,求解这类问题依赖平行于试件表面方向(r方向)的信息,因此均匀壁厚减薄脉冲涡流检测解析模型不再适用.
为扩大解析模型求解问题的范围,本文提出平底孔试件脉冲涡流检测解析模型.该模型的解析表达式中既包含试件z方向的信息,也包含r方向的信息,且当平底孔半径趋向于无穷大时,可简化为均匀壁厚减薄脉冲涡流检测解析模型,因而具有更广泛的应用.
然而,平底孔试件脉冲涡流检测解析模型在r和z方向均存在介质分界面,因此其边界条件复杂.关于如何求解此类问题,Theodoulidis和Bowler做了探索,得到了线圈位于试件边缘时的阻抗解析表达式[19,20].其所用方法的特点是利用TREE法中截断区域边界处的磁约束条件构造磁矢位表达式,利用试件边缘处(试件与空气交界处)的边界条件求解横向波数,从而避免了复杂边界条件的求解.利用该方法,涡流检测通孔试件[21]等问题同样得到了解决.然而,上述方法仅适用于非铁磁性材料,对于铁磁性材料,由于其磁导率远大于1,用该方法得到的横向波数的特征方程中包含复杂的复变量Bessel函数项,求解复杂.因此该方法在铁磁性材料中的应用受到了一定的限制[22].
本文采用不同的思路求解平底孔试件脉冲涡流检测解析模型.假设平底孔所在层导体与空气区域的电磁波横向波数和纵向波数均相同,且横向波数为仅与r方向结构有关的实数,纵向波数为与该层横向波数和导体区域材料有关的复数.首先,在上述假设的基础上应用电磁波反射和折射理论,构造包括平底孔所在层在内的各层电磁波动方程,其次,将Cheng等[23]的矩阵法扩展,用扩展的传递矩阵法对波动方程进行求解,得到接收线圈感应电压表达式.最后,将该模型应用到16MnR平底孔试件检测实例,并对平底孔试件进行实验分析,通过对比模型计算结果和实验结果,验证模型的正确性.
2 平底孔试件脉冲涡流检测解析模型
激励和接收线圈位于平底孔试件上方的脉冲涡流检测解析模型如图1,其中试件为线性、均匀且各向同性的介质;试件厚度为z3,所含平底孔半径为c,深度为d.应用TREE法将模型求解域限制在r=h的圆柱体内,且为便于分析,按照z方向边界条件的不同,将整个求解域划分为5层,线圈位于1—2层,平底孔位于4层.根据r方向边界条件的不同,4层可继续划分为空气区域和导体区域2个子区域,r=c为这两个子区域的分界面.
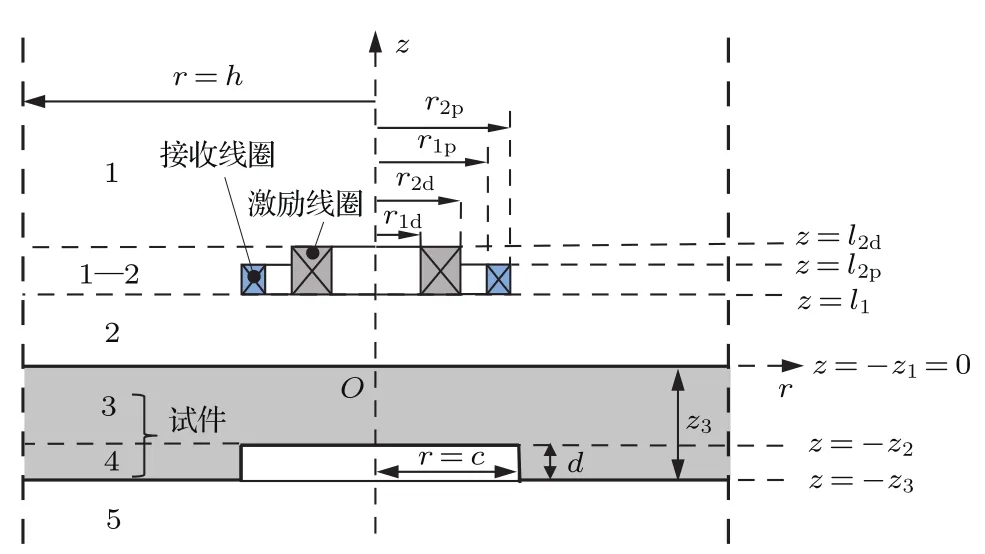
图1 (网刊彩色)激励和接收线圈置于平底孔试件上方Fig.1.(color on line)D iver and pickupcoils located above the plate with a fl at-bottomhole.
2.1 根据反射和折射理论构造各层磁矢位A表达式
为建立图1所示平底孔试件脉冲涡流检测解析模型的解析解,首先考虑激励电流为谐波电流的情况.应用时谐电磁场的Maxwell方程组和分离变量法,忽略ω2µ0µrε项[24],矢量磁位A可表示为[8]

式中,i为层数;αn为特征方程FiJ1(αnh)+DiY1(αnh)=0的第n个根,表示电磁波横向波数[14];表示电磁波的纵向波数[25],其中,j为虚数单位;ω为谐波电流角频率;ε为介电常数;µ0为真空磁导率;µri和σi分别为i层相对磁导率和电导率;J1(αr)和Y1(αr)分别为一阶第一类和第二类Bessel函数;Ci,Bi,Fi,Di为系数;N s为求和项数.
(1)式中的Bessel函数项表示电磁波沿r方向的传播情况,指数项表示电磁波沿z方向的传播情况,其中e−βinz表示电磁波沿 +z方向传播,称为正向行波;e+βinz表示电磁波沿−z方向传播,称为反向行波.对于图1所示的1—3,5层,1层仅有正向行波,则C1=0;5层仅有反向行波,则B5=0.其他层既有正向行波也有反向行波,则Ci,Bi均不为0.同时考虑到Y1(αr)在r=0处发散,则系数Di必须恒等于0,即D1=D2=D3=D5=0.基于上述分析,1—3,5层的磁矢位A可分别表示为

其中,由于D1=D2=D3=D5=0,αn的特征方程FiJ1(αnh)+DiY1(αnh)=0可简化为J1(αnh)=0.
对于4层,由于r和z方向都存在介质分界面,边界条件复杂[20],因此在构造磁矢位A表达式时,除了依据电磁波传播规律,还需考虑求解的方便性.
由(1)式可知,磁矢位A的表达式由两部分组成:
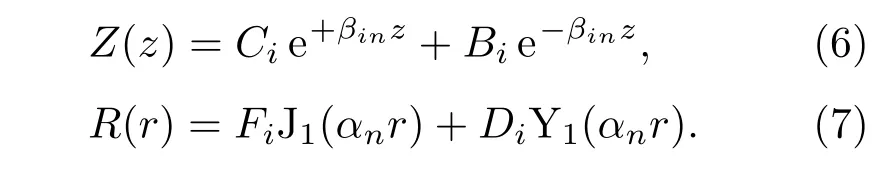
在构造空气区域表达式时,可以将(6)式中的βin替换成αn,或将(7)式中的αn替换成βin[8].对于4层,为求解方便,一般需保证空气和导体区域磁矢位A表达式中的指数项相同[20],因此我们选择第二种方式,则4层表达式为
因为沿z方向,4层正向行波和反向行波都存在,C4,B4均不为0.沿r方向,4层导体区域仅有入射波,且由于该区域不存在r=0点,则D4/=0.4层空气域表达式中D′4=0,且该区域存在入射波和r=c交界面处产生的反射波,入射波用表示,反射波用表示,叠加之后为,根据Bessel函数的性质,J1(−x)=−J1(x),将其整理为F4J1(β4nr),则(8)式可重新写为

(9)式空气区域和导体区域的横向波数不同,因此求解得到αn的特征方程中含有Bessel函数的复数项.当试件为铁磁性材料时,αn的特征方程表达式复杂,难以求解.基于此,本文对(9)式做进一步简化.假设4层空气和导体区域横向波数相同,为仅与r方向结构相关的实数,纵向波数相同且仅与该层横向波数和导体区域材料相关,同时为区别于其他层,4层的横向波数用符号qn表示,则

根据r=c处的法向边界条件,重新整理(10)式,得到

通过r=c处的切向边界条件求解系数D4,
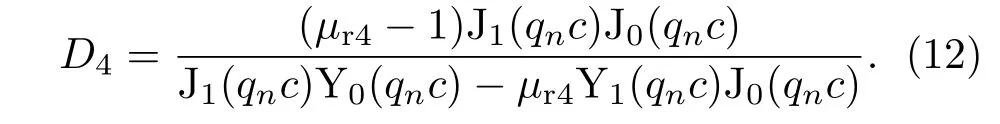
将D4代入J1(qnh)+D4Y1(qnh)=0中,化简之后得到横向波数qn的特征方程
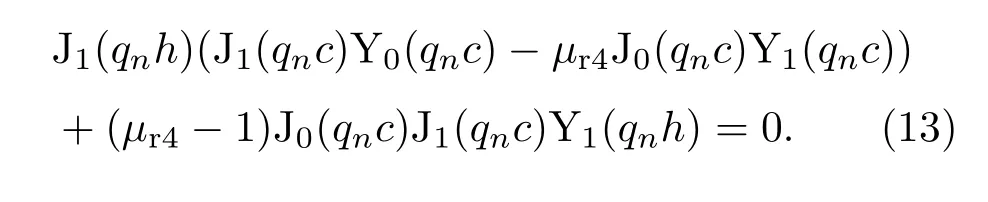
设qnh=xn,ref=c/h,µr4−1≈ µr4,则上述特征方程的解即为(14)式所示函数f(x)的零点,

由于函数f(x)表达式中的Bessel函数项不含复数项,因此用一般的求根方法即可求解.本文选用牛顿法.因c=0可看作平底孔试件脉冲涡流检测解析模型的极限情况,则c=0对应的特征方程J1(xn)=0的解可作为用牛顿法的初值,将其代入(15)式所示的牛顿法迭代公式中,经过一定次数的迭代,即可求得函数f(x)的所有零点.qn=xn/h,则横向波数qn的解也可得到.

2.2 利用扩展的矩阵法求解感应电压表达式
要求得接收线圈的感应电压表达式,需对1—5层磁矢位A((2)—(5)式和(11)式)进行求解.根据电磁波动理论,接收线圈所处空间的电磁波可分为入射波和反射波,接收线圈接收到的实际是反射波的变化率,因此求解接收线圈中的感应电压其实就是求解反射波.反射波等于入射波和反射系数的乘积,由(3)式可知,入射波幅值为C2,反射系数用T(α)表示,则求解反射波即求解C2和T(α).Cheng的矩阵法[23]因表达式结构简单而被广泛应用,因此,本文欲采用矩阵法对C2和T(α)进行求解,然而,由于Cheng的矩阵法仅适用于均匀壁厚减薄脉冲涡流检测解析模型,不能直接用于求解本文研究的r和z方向都存在介质分界面的情况,为此,需将Cheng的矩阵法扩展.
根据(16)和(17)式所示的层与层之间的法向和切向边界条件和(18)式所示的Bessel函数正交特性[8],(2)—(5)式和(11)式磁矢位A表达式中系数Bi和Ci之间的关系如(19)和(20)式所示.

其中,Wi为r方向结构系数,对于均匀壁厚减薄脉冲涡流检测解析模型,Wi=1;对于本文研究的平底孔试件脉冲涡流检测模型,当第i层r方向存在介质分界面时,Wi,Wi−1,Wi+1可表示为

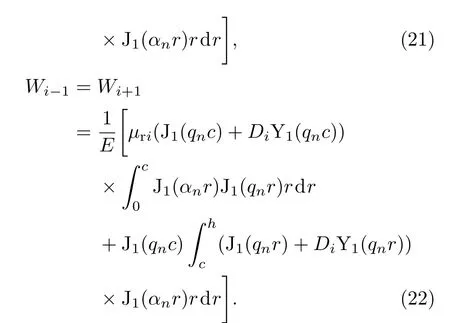
根据Cheng的矩阵法,将系数表示成矩阵形式,系数之间的关系用转换矩阵表示,则(19)和(20)式表示的系数之间的关系为

应用扩展的矩阵法对C2和T(α)进行求解,结果如(28)和(29)式所示.
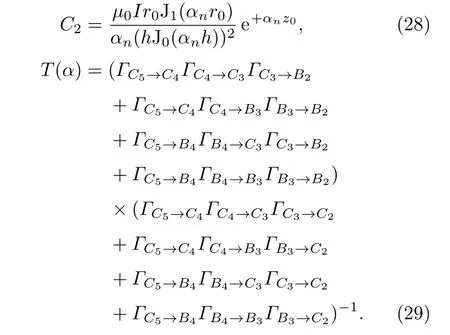
则谐波激励时,接收线圈的感应电压表达式为
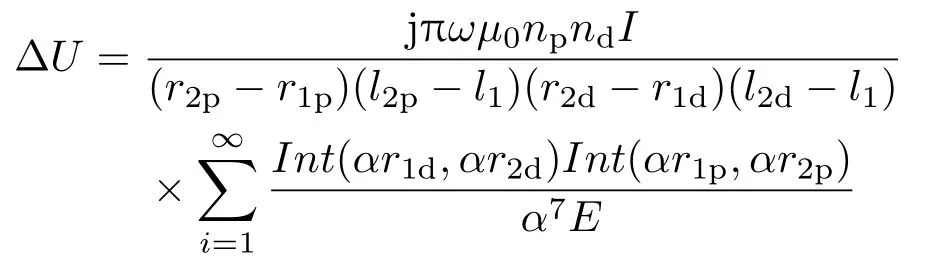

根据傅里叶变换,脉冲涡流激励可看作一系列谐波激励的叠加,因此将各谐波感应电压相加,并对结果做离散傅里叶逆变换,即可得到脉冲涡流激励时接收线圈中的时域感应电压∆U(k)序列:

其中,N为采样点数,k=1,2,3,...,N;ωm为各谐波频率;I为正弦电流幅值;l1为探头提离,l2d和l2p分别为激励、接收线圈上端面到试件的距离;r1d和r2d分别为激励线圈的内、外半径;r1p和r2p分别为接收线圈的内、外半径,nd是激励线圈匝数,np是接收线圈匝数.
3 解析模型验证
为验证平底孔试件脉冲涡流检测解析模型的正确性,将该模型应用到16MnR平底孔试件检测中,并对其进行实验分析.实验所用系统为实验室自主研发的HSPEC-III脉冲涡流检测系统[26];所用平底孔试件为如图2所示的16MnR试件,试件厚度z3为20mm,试件中的平底孔深度d为8mm,平底孔半径分别为10,25,50,75,90 mm.为便于检测信号分析,平底孔试件中设有不含平底孔的区域,在图2中标记为参考区域.在探头提离l1为5 mm时对图2所示的平底孔试件进行实验,得到参考区域和不同半径平底孔区域的感应电压信号,探头参数见表1.
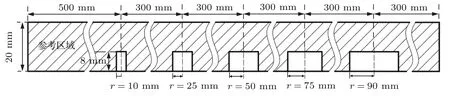
图2 平底孔试件示意图Fig.2.The d iagramof the plate with diff erent fl at bottomholes.

表1 探头参数Tab le 1.Parameters of the probe.
设16MnR试件的相对磁导率µr3= µr4=500,电导率σ3=σ4=1.6MS/m,将表1所列探头参数、探头提离l1=5 mm、试件厚度z3=20 mm、平底孔深度d=8mm和不同的平底孔半径值代入平底孔试件脉冲涡流检测解析模型的感应电压表达式,即(33)式,计算参考区域和不同半径平底孔区域的感应电压信号.
为比较解析模型计算结果与实验结果,设参考区域的感应电压信号为参考信号,其他区域的信号大小用其相对于参考信号的欧氏距离[27]表示.考虑到脉冲涡流感应电压信号通常在对数坐标系下显示[26],则对数坐标系下,其他区域信号相对于参考信号的欧氏距离可表示为


图3 解析计算和实验结果比较Fig.3.Comparison of the analy tical and experimental resu lts.
其中,U参考表示参考区域感应电压信号,U其他表示其他区域感应电压信号.
将解析计算得到的感应电压信号与实验得到的感应电压信号代入(34)式,则可得到平底孔半径不同时的感应电压信号相对于参考信号的欧氏距离.对比解析计算结果与实验结果,如图3所示,解析计算结果与实验结果基本符合,从而验证了平底孔试件脉冲涡流检测解析模型的正确性.
4 结 论
本文提出了平底孔试件脉冲涡流检测解析模型,弥补了现有均匀壁厚减薄脉冲涡流检测解析模型仅含试件厚度(z方向)信息的不足.在该模型求解过程中,由于铁磁性构件磁导率远大于1,平底孔所在层的特征方程难以计算,本文首先应用电磁波反射和折射理论构造各层磁矢位A的表达式;然后通过扩展的传递矩阵法对其求解,获取接收线圈感应电压表达式.将模型应用到16MnR平底孔试件检测中,并对其进行实验验证.解析模型计算结果与实验结果基本符合,验证了模型的正确性.平底孔试件脉冲涡流检测解析模型可对更多脉冲涡流检测问题提供理论指导,具有重要的工程意义.下一步的研究工作将围绕该模型在脉冲涡流检测中的应用展开.
[1]Fan MB,Y in Y D,CaoBH2012Acta Phys.Sin.61 088105(in Chinese)[范孟豹,尹亚丹,曹丙花2012物理学报61 088105]
[2]Fu J J,LeiY Z 2016J.Sci.Instrum.37 617(in Chinese)[付剑津,雷银照2016仪器仪表学报37 617]
[3]Yang L J,Su JM,GaoSW,Liu B2016NDT40 10(in Chinese)[杨理践,孙靖萌,高松巍,刘斌2016无损探伤40 10]
[4]Kang X W,Fu Y W 2011Nondestr.Test.33 40(in Chinese)[康小伟,付跃文 2011无损检测 33 40]
[5]W u X J,Zhang Q,Shen G T2016J.Sci.Instrum.37 1698(in Chinese)[武新军,张卿,沈功田2016仪器仪表学报37 1698]
[6]Dodd C V,Deeds W E 1968J.Appl.Phys.39 2829
[7]Theodou lid is TP,Kriezis E E 2005J.Mater.Process.Technol.161 343
[8]Theodou lid is TP,Kriezis E E 2006Eddy Curren t Canonical Problems(with applications tonondestructive evaluation)(Forsyth:Tech Science Press)pp93–135
[9]Fan MB,Huang P J,Ye B,Hou D B,Zhang G X,Zhou Z K2009Acta Phys.Sin.58 5950(in Chinese)[范孟豹,黄平捷,叶波,侯迪波,张光新,周泽魁 2009物理学报 58 5950]
[10]Chen X L,Lei Y Z 2015Chin.Phys.B24 030301
[11]Xu Z Y,W u X J,Li J,Kang Y H2012NDT&E In t.51 24
[12]Tian G Y,Li Y,Mandache C 2009IEEE Trans.Magn.45 184
[13]Li J,W u X J,Zhang Q,Sun P F 2015NDT&E In t.75 57
[14]Fu F,Bowler J 2006IEEE Trans.Magn.42 2029
[15]Xu Z Y 2012Ph.D.D issertation(W uhan:Huazhong University of Science and Technology)(in Chinese)[徐志远2012博士学位论文(武汉:华中科技大学)]
[16]Cheng W,Komu ra I2012Proceedings of the 9th In ternational Conference on NDE in Relation toStructura l In tegrity for Nuclear and Pressurized Componen tsSeattle,USA,May 22–24,2012 p336
[17]W ang J,Teng Y P,Fu Y G,Sun MX,Liu Z B,Fan Z Y,Shi K2013Nondestr.Test.35 54(in Chinese)[王健,滕永平,傅迎光,孙明璇,刘再斌,范智勇,石坤 2013无损检测35 54]
[18]X ie S,Chen Z,Takagi T,UchimotoT2012NDT&E In t.51 45
[19]Bowler J R,Theodou lid is TP 2006J.Phys.D:Appl.Phys.39 2862
[20]Theodou lid is TP,Bowler J R 2010IEEE Trans.Magn.46 1034
[21]Theodou lidis TP,Bowler J R 2005Rev.Prog.Quantit.Nondestr.Eva l.24 403
[22]Zhang Q,W u X J,Li J,Sun P F 2014Proceedings of the 19th In ternational W orkshopon E lectromagnetic Nondestructive EvaluationXi’an,China,June 23–28,2014 p95
[23]Cheng C C,Dodd C V,DeedsW E 1971In t.J.Nondestr.Test.3 109
[24]Feng C Z,Ma X K2000An Introduction toEngineering E lectromagnetic Fields(Beijing:Higher Education Press)p228(in Chinese)[冯慈璋,马西奎2000工程电磁场导论(北京:高等教育出版社)第228页]
[25]Yang Z 2009Ph.D.Dissertation(Shandong:China University of Petroleum)(in Chinese)[杨震2009博士学位论文(山东:中国石油大学)]
[26]Xu Z Y,W u X J,Huang C,Kang Y H2011J.Huazhong Univ.Sci.Techn(Nat.Sci.Ed.)39 91(in Chinese)[徐志远,武新军,黄琛,康宜华 2011华中科技大学学报(自然科学版)39 91]
[27]X ie MX,GuoJ Z,Zhang HB,Chen K2010Computer Eng.Sci.32 92(in Chinese)[谢明霞,郭建忠,张海波,陈科2010计算机工程与科学32 92]
PACS:81.70.Ex,03.50.De,41.20.–qDOI:10.7498/aps.66.038102
Analy ticalmodeling for the plate with a fl at-bottomhole based on the refl ection and transmission theory in pu lsed eddy cu rren t testing∗
Zhang Qing Wu Xin-Jun†
(School ofMechanical Science and Engineering,Huazhong University of Science and Technology,W uhan 430074,China)(Received 8 Ju ly 2016;revised manuscript received 26 October 2016)
Ferromagnetic structures such as pipes or vessels are widely used in petroleum,chemical and power generation industries.Periodical nondestructive testing(NDT)is vital for continued safe operation.As a NDTtechnology,pu lsed eddy current testing(PECT)technology which is excited by a square-wave pulse rather than a sinusoidalwaveformhas been widely used for its advantages of non-contact and acquisition of information at various depths in one excitation process.In PECT,the analyticalmodeling is important because it gives a better understanding of the signaland benefi ts the inverse process of PECTin extracting information of structures.The foundation of theoreticalmodelof PECTis the Dodd-Deedsmodel presented by Dodd and Deeds in 1968,Theodou lidis and Kriezis represented the integral solution of Dodd-Deedsmodel in the formof series by using the truncated region eigen function expansion(TREE)method.Using the Dodd-Deedsmodel and the TREE method,other analyticalmodelings have been solved.However,most modelings assume that the wall thinning of the specimen is uniform,and the analytical solution only contains the variab les in the z direction(the direction perpendicular tothe surface of the specimen),such as the thickness of the specimen.W ith the rapid development of PECT,problems such as the footprint of the probe,the quantitative analysis of local wall thinning alsoneed tobe solved.These problems are related tothe variable in the r direction(the direction parallel tothe surface of the specimen),sothe analytical modelings mentioned above are not available any more.Tosolve these prob lems,the analyticalmodeling of the plate with a fl at-bottomhole is proposed.Considering the fact that the boundary condition in the analyticalmodeling of the plate with a flat-bottomhole is complicated,the assumption that the transverse wave number and the longitudinal wave number in the layer where the fl at-bottomhole located are the same ismade in this paper,and the transversewave number is set tobe only related tothe structure in the r direction.Firstly,the expressions ofmagnetic vector potential in all the layers are obtained by using the reflection and refraction theory of electromagnetic wave.Then the analytical solution is solved based on the extended Cheng’smatrix method by introducing the construction coeffi cient Wn.Finally,the 16MnR specimen with the flat bottomholes is conducted as an example,and experiments are carried out.The good agreement between resu lts calculated by the analyticalmodel and the experimental resultsmeasured verifies the developed analyticalmodel.
pu lsed eddy current testing,reflection and transmission theory,flat-bottomhole,analytical modeling
10.7498/aps.66.038102
∗国家重点研发计划(批准号:2016YFC 0801904)和国家自然科学基金(批准号:51077059)资助的课题.
†通信作者.E-mail:xin junwu@mail.hust.edu.cn
*Project supported by the National Key Research and Development Programof China(Grant No.2016YFC0801904)and the National Natu ral Science Foundation of China(G rant No.51077059).
†Corresponding author.E-mail:xin junwu@mail.hust.edu.cn

