黑洞吸积盘系统的喷流加速机制研究∗

徐佳迪姜志雄龚小龙2)†

1)(长江大学物理与光电工程学院,荆州 434023)2)(北京师范大学天文系,北京 100875)(2016年8月22日收到;2016年9月25日收到修改稿)

黑洞吸积盘系统的喷流加速机制研究∗

徐佳迪1)姜志雄1)龚小龙1)2)†

1)(长江大学物理与光电工程学院,荆州 434023)2)(北京师范大学天文系,北京 100875)(2016年8月22日收到;2016年9月25日收到修改稿)

提出了一种从旋转黑洞吸积盘热冕系统中提取能量的喷流加速机制.在吸积盘热冕中,通过求解广义相对论框架下的盘冕系统的动力学方程,得出了吸积盘热冕内区的磁场强度;进一步根据黑洞磁层的电路理论推导出喷流功率的解析表达式.结果表明:模型中喷流功率随着黑洞自转参数a∗和磁力矩参数∆ε的增加而明显增大,并且大部分功率应来自于在吸积盘热冕系统的内区.此外,用一组高功率喷流的活动星系核样本探讨了该喷流加速机制,分析表明所有高功率喷流源能被模型喷流功率所拟合.

吸积,吸积盘,喷流,冕

1 引 言

众所周知,大尺度的射电喷流普遍存在于活动星系核、X射线双星等各类天体中.尽管喷流的形态千差万别,但它们共同的特征是气体从致密天体的核心部分被高速抛射出去,形成充满热等离子体的柱状结构.关于喷流加速和准直的详细机制目前还尚未有公论,但是喷流与磁化吸积盘或中心大质量黑洞存在着紧密联系,这已经被哈勃太空望远镜、X射线望远镜和甚长基线干涉仪的观测所证实.很多学者一致认为射电喷流的形成与天体中心的旋转黑洞和吸积盘的大尺度磁场有关[1−3].

为了解释喷流的加速机制,学者们已经提出了一些喷流的理论模型,常见的有Blandford-Znajek(BZ)机制[4],Bland ford-Payne(BP)机制[5]、辐射压加速喷流机制[6],Meier[7]提出的杂化喷流模型等.在BZ机制中,Kerr黑洞的旋转能量可以被连接黑洞视界的大尺度极向磁场提取出来,用以解释喷流的功率.BP机制对于解释喷流的产生也是一种重要的机制.在该机制中,吸积物质的能量和角动量被盘表面的磁场从吸积盘中提取出来.在上述工作的基础上,Macdonald和Thorne[8]在广义相对论框架下的Kerr 3+1时空中重新定义和拓展了BZ理论并利用等效电路得出了黑洞功率和盘功率的解析表达式.

大尺度磁场在喷流的加速机制中有着极其重要的地位,观测已发现致密天体附近明显地存在着大尺度磁场.理论研究已表明大尺度磁场的强度与吸积盘系统的相对高度成正比[9,10],通常薄盘的大尺度磁场强度较弱,而径移主导吸积流[11,12]或者是热冕极向磁场往往较强.正是由于热冕的厚度比薄盘大,因此冕区的磁场及其发射的喷流功率应该明显比薄盘大[13].最近Cao等[14,15]指出,对于径移主导吸积流,仅BZ机制是不能解释BL Lac天体和射电星系的喷流的加速.在高吸积率标准薄盘情况下,研究也表明部分射电类星体的喷流功率会远高于BZ机制所能达到的上限,因而喷流应该是被盘冕中的磁场加速的[16].

天文上估计喷流功率的方法对于量化活动星系核中央引擎的输出功率相当重要.到目前为止,观测估算喷流功率通常有三种方法:第一种方法是利用射电望远镜数据,例如1999年W illot等[17]最早在151频段用来自射电瓣的通量估计了喷流的功率值,并给出了喷流功率与射电光度之间的经验公式;第二种方法是利用X射线天文卫星观测喷流与周围星际物质产生的孔洞(cavity)数据,该方法主要利用喷流形成的孔洞向外膨胀的动能去估算喷流功率,例如Allen等[18](2006年),McNamara等[19](2011年),Zhang等[20](2014年)的工作;第三种方法主要是Ghisellini等[21,22](2009,2010年)的工作,他们在Fermi天文卫星的观测数据基础上利用多波段能谱拟合的方法估算出了相应天体的喷流功率、吸积率等数据.

最近,我们提出了一种广义相对论框架下的吸积盘热冕模型[23],并利用Monet-Carlo方法模拟出了不同参数下盘冕系统的能谱;进一步用盘冕情况下磁场加速喷流模型拟合了一组射电噪类星体样本的喷流功率观测值,但结果表明理论值无法解释少数具有高喷流功率值的样本[24].

作为以上工作的延续,本文进一步改进本课题组所提出的模型,并重新选取一组具有更高喷流功率值的样本进行观测拟合.本文的第二部分和第三部分是对理论模型的描述;第四部分用所提模型去拟合一组具有极高喷流功率值的耀变体(Blazar)样本(一类活动星系核),其喷流功率的天文观测估计值选自Ghisellini等[21]的工作;第五部分是对结果的总结和展望.

2 吸积盘和热冕

本文在牛顿力学的吸积盘-冕模型的基础上[25],研究广义相对论框架下的吸积盘热冕系统.在该盘冕系统中几何厚光学薄吸积盘环绕旋转Kerr黑洞,同时吸积盘上下被两层磁化的平板冕包夹,部分吸积物质引力势能耗散在热冕中.研究中采用了由Novikov和Thorne[26]以及Page和Thorne[27]提出的广义相对论下稳态的、几何对称的标准薄盘解.在他们的模型中,假设盘的内边缘不存在由磁场产生的应力,即“无力矩内边界条件”.在这种情形下,吸积气体如果到达稳定轨道的最小半径r=rms处就会离开吸积盘以螺旋运动的方式掉进黑洞.所以,与位于r≥rms处的吸积气体相比,位于r＜rms处的吸积气体密度实际上趋于0,这就意味着没有黏滞应力作用在吸积盘r=rms处的切面上.此时耗散在吸积盘热冕系统单位表面积上的总引力势能由以下公式得出[27]:

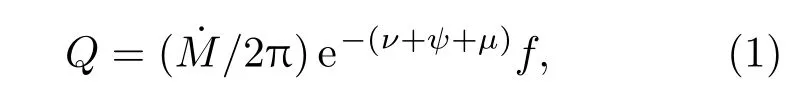
其中,盘中物质的比能量 E+和比角动量 L+可表示为

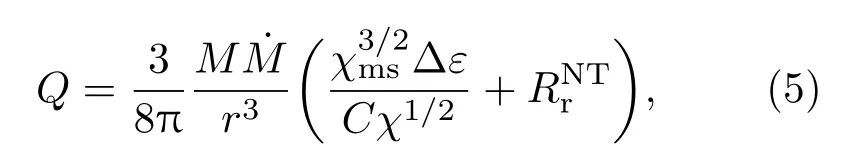
同时耗散在冕中的功率为

式中,Pm为磁压,υP为盘中磁通量垂向传输速度.我们假设该速度与其内部的Alfven速度 υA成正比,即υP=bυA.吸积盘的垂向压力平衡方程为

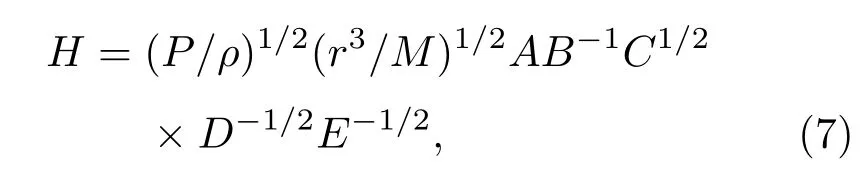
这里H是吸积盘的高度;P和ρ分别为压强和盘的密度;A,B,C,D,E是广义相对论修正因子[26].吸积盘能量守恒方程为[26]

这里α是黏滞系数,计算中取α=0.3.

吸积气体的状态方程为

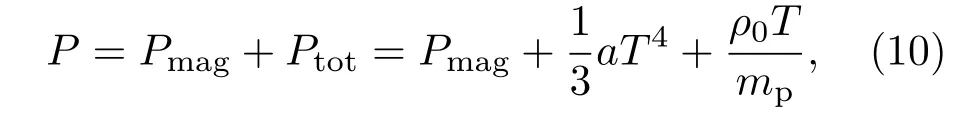
这里Ptot是盘的总压强(气压与辐射压之和),a是辐射常数,mp是质子静止质量,T和 ρ0分别为盘内温度和物质密度.通常磁压可取

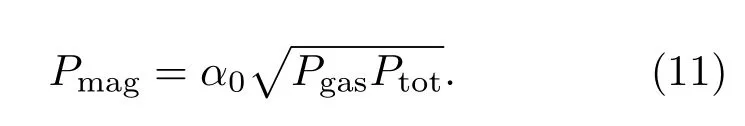
而盘冕系统中能量传输方程为

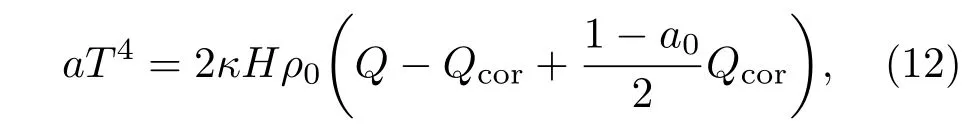
这里κ为 Rosseland常数,a0是盘冕反射反照率,通常反照率非常低.并且大部分来自盘冕的事件光子碰到吸积盘后会以黑体辐射形式被辐射出去,本文计算中取a0=0.1[29].

用数值方法解方程(5)—(12),可得出冕中耗散的功率Qcor,它是关于半径r的函数.求解方法与我们前期工作相同[23].

3 盘冕喷流

下面我们讨论由热冕中磁场驱动喷流的喷流加速机制.考虑到部分盘冕功率Qcor被用来加热冕,因此热冕中的磁能密度为

式中t0=Hcor/vdiss为耗散时间,其中Hcor是盘冕的高度.而耗散速度vdiss由吸积盘对冕的加热过程决定,计算中取vdiss=0.01c,η=0.5.

对于大尺度磁场,一些学者认为由发电机机制产生的小尺度磁场可以生成大尺度磁场[9,10],并且盘冕系统中的极向磁场强度取决于冕中磁流管的高度和磁重联的能力.为方便计算,我们假设大尺度磁场极向分量的强度可近似表示为

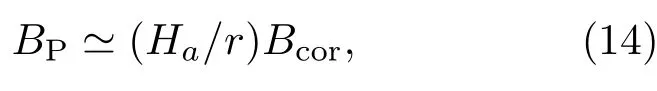
式中Ha为冕中磁流管的典型高度.通常磁流管的高度会明显大于盘的厚度,在本文计算中取Ha=2rms,rms为吸积盘最内稳定轨道半径.

图1给出了黑洞旋转参数a∗取不同值时BP随径向参数ξ=r/rms的变化.注意磁场BP以为单位,˙M是吸积率,M是黑洞质量.观察图1,我们发现大尺度极向磁场强度BP的值随着盘半经r的增大而减小,近似地表现为负幂率关系.该结果与Bland ford等[5]的工作和预期是相符的,在其提出的BP过程中就直接阐明吸积盘上的大磁度磁场应满足B=r−3的关系[5].通过图1(a)可见,磁场强度随着黑洞旋转参数a∗的增加而增强.事实上由Kerr黑洞的Frame-dragging效应可知,黑洞自转加速时盘冕系统内区磁场的明显增强应是一个可以预期的结果.从图1(b)可见随着磁力矩参数∆ε的增大,磁场强度会明显增强.显然参数∆ε越大意味着从吸入区转入盘内区的能量越多,这将直接导致内区磁能密度的增大.

图1 极向磁场Bpcor随经向参数ξ= r/rms的变化 (a)实线、划线、点线分别对应着黑洞自转参数a∗=0.9,0.5,0.1,计算中取 ∆ε=0.5;(b)实线、划线、点线分别对应着参数∆ε=1,0.5,0,计算中a∗=0.5Fig.1.The poloidal magnetic fieldvaries with the rad ius parameterξ=r/rms:(a)For the deferent b lack hole spin a∗=0.9,0.5,0.1(solid,dashed,dotted lines),∆ε=0.5 is adopted in the calcu lations;(b)for the deferent parameter∆ε=1,0.5,0(solid,dashed,dotted lines),a∗=0.5 is adopted in the calcu lations.

Macdonald和Thorne[8]在研究黑洞能层的基础上创新性地提出了等效电路理论,在该理论中大尺度磁场将黑洞与吸积盘转动动能以电磁能流的形式转移出来,从而给喷流提供能量来源,其电磁功率解析式可表示如下[8]:

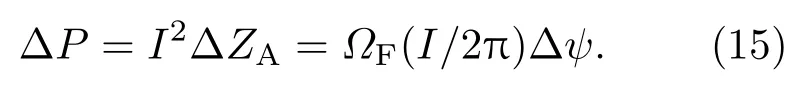
其中I和∆ψ分别为等效电流和相邻磁层间的磁通量,ΩF是磁力线角速度.

在Macdonald和Thorne[8]的研究基础上,我们也提出一种改进型等效电路来计算来自盘冕系统的喷流功率[30−32].在推导喷流功率的过程中用到了如下公式:

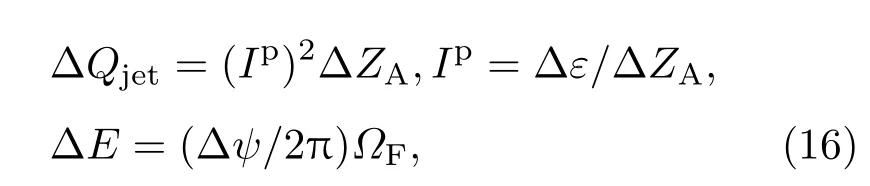
式中∆E是盘冕系统旋转产生的电动势,Ip是热冕中每个回路的极化电流,∆ψ和∆ZA分别为相邻磁层间的磁流和相应加速区的阻抗.磁通量∆ψ可表示为

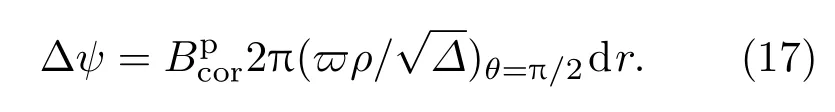
通常加速区阻抗与吸积盘阻抗比值可决定磁力线角速度.当吸积盘阻抗很低时可取ΩF≃ΩD[8].在我们提出的盘冕模型中,考虑到吸积盘阻抗相对于加速区阻抗较低,可假设盘冕中的磁力线角速度为

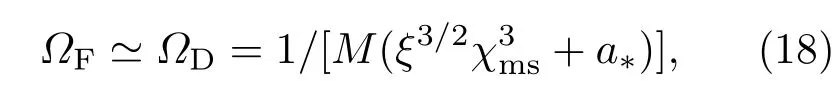
其中径向参数χms定义为相邻磁层间的负载阻值∆ZA可表示为[8]

以上各式中涉及的各Kerr度规因子为[33]

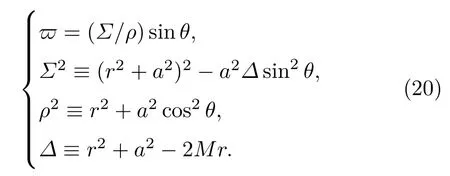
联合(14)—(20)式并将(16)式沿径向积分,可得喷流功率的解析表达式为

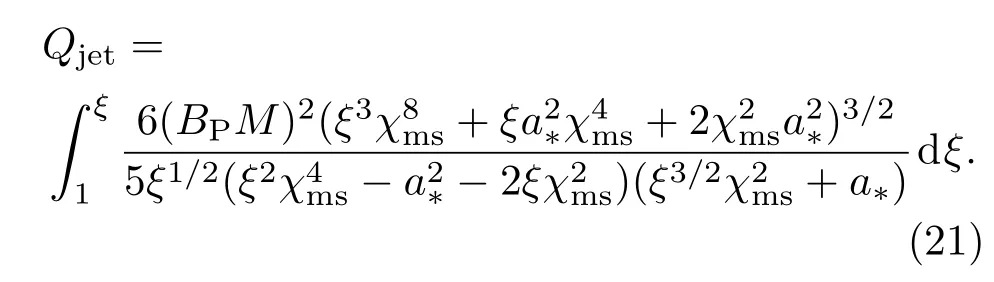
图2 模型喷流功率Qjet随黑洞自转参数a∗的变化 图中实线、划线、点线分别对应着吸积率˙m=0.5,0.3,0.1,计算中取∆ε=0,M=109M⊙Fig.2.The curves of model jet power Qjetversus b lack hole spin parameter a∗for d iff erent accretion rate˙m=0.5,0.3,0.1(solid,dashed,dotted lines).∆ε=0,M=109M⊙are adopted in the calcu lations.

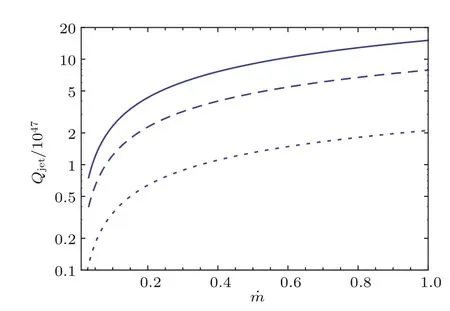
图3模型喷流功率Qjet随吸积率˙m的变化图中实线、划线、点线分别对应着参数∆ε=1,0.5,0.1,计算中取a∗=0.5,M=109M⊙Fig.3.The curves ofmodel jet power Qjetversus accretion rate˙mfor d iff erent parameter∆ε=1,0.5,0.1(solid,dashed,dotted lines).a∗=0.5,M=109M⊙are adopted in the calcu lations.

由(21)式可做喷流功率Qjet随黑洞自转参数a∗变化的曲线,如图2所示.观察图2我们发现模型喷流功率Qjet随着黑洞旋转参数a∗的增加而增大.此外,我们也给出了在不同参数下喷流功率Qjet随吸积率变化的规律,如图3所示,很明显喷流功率随吸积率的增大而单调递增.应该注意的是,在计算中,(21)式中的积分上限取ξ=30,即只计算了来自吸积盘30个最内稳定半径rms范围内的喷流功率.选择以上积分范围基于两个方面的考虑:一方面是基于观测,Biretta等[34]利用甚长基线干涉测量技术观测了邻近星系M87中心喷流的亚毫角秒结构,发现其射电喷流的加速区应处于中心天体附近几十个Schwarschild半径区域以内;二是通过计算我们发现当积分上限取ξ＞30时,喷流功率Qjet值的增大变化已很小,这也直接表明绝大部分喷流功率应来自于在吸积盘热冕系统的内区,可见理论模型与观测能较好地符合.

为了将我们模型的喷流功率与BZ机制的喷流功率相比较,给出当旋转黑洞视界面的磁场B⊥已知时BZ功率的表达式为[4]

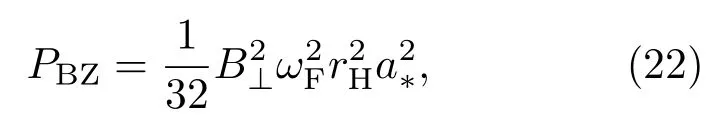
其中rH是视界半径,是用来描述磁力线角速度ΩF影响相对于黑洞角速度ΩH影响比例的因子.如果ΩF=1/2ΩH,BZ机制的输出功率达到最大,计算中我们取ωF=1/2.同时Moderski等[35]在考虑到黑洞视界面磁压与吸积流最内层的冲击压相平衡基础上得出磁场B⊥与吸积率之间的关系式为

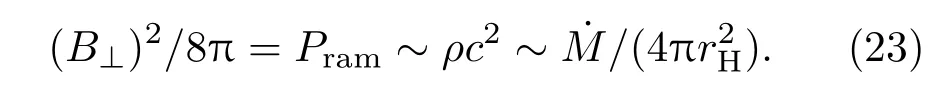
由(23)式我们可以得出黑洞视界面的磁场强度为

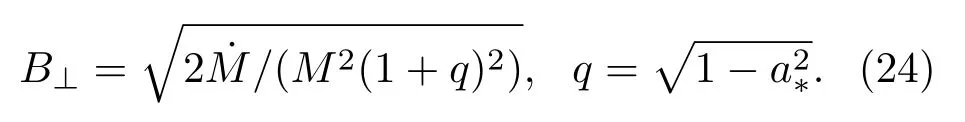
4 观测拟合

为了将理论模型与观测数据进行比较分析,我们选取了一组包含23个高喷流功率耀变体(Blazar)的天文样本.样本中的中心黑洞质量、吸积盘光度、喷流功率观测值取自Ghisellini等[21]的工作.我们选取的样本如表1所列,表中第一和第二列为国际天文联合会天体名称及其红移,第三列是以太阳质量为单位的中心黑洞质量,第四列为以erg.s−1为单位的吸积盘热光度,第六列为以erg.s−1为单位的喷流功率观测值.表1中第五列是依据(25)式计算出的相应的无量纲吸积率,当活动星系核的中央黑洞质量给定时,通过热光度Lbol可以估测这些射电源的吸积率.无量纲吸积率可表示为

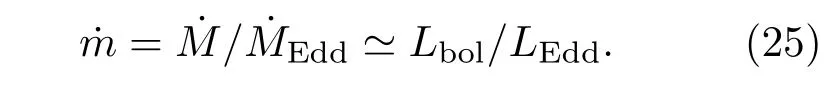
表1 具有23个高喷流功率天体的观测样本Tab le 1.An observational sample consisting of 23 ob jectswith high jet power.

在图4和图5中,我们给出了吸积率˙m和喷流功率Qjet之间的关系.利用(21)式可以计算出不同参数下模型的喷流功率,即图5中的各条曲线.而从旋转黑洞中提取的功率(即BZ功率)可通过(22)式来计算,结果见图4.在图4和图5中的小方块中心对应23个天体的吸积率和喷流功率值.图4中的实线代表BZ机制所能达到的最大喷流功率值.图5中各条曲线的含义如下:划线代表当参数∆ε=0.3时盘冕喷流的功率值,相应的其曲线右下区域为∆ε＜0.3时盘冕模型能拟合的功率值范围.

图4 BZ功率与吸积率的关系 图中实线、点线分别对应着黑洞自转a∗=0.99,0.5时的BZ功率,计算中取M=1010M⊙Fig.4.The BZ power versus the accretion rate˙mfor the d iff erent b lack hole spin values:a∗=0.99(solid lines),a∗=0.5(dotted lines),M=1010M⊙is adopted in the calcu lations.

图5喷流功率Qjet与吸积率的关系 图中实线、点划线、划线、点线分别对应着参数∆ε=1,0.5,0.3,0,计算中取a∗=0.5,M=109M⊙Fig.5.The jet power versus the accretion rate˙mfor the d iff erent parameter values:∆ε=1,0.5,0.3,0(solid,dot-dashed,dashed,dotted lines).a∗=0.5,M=109M⊙are adopted in the calcu lations.

观察图4和图5,我们得出以下结论:1)BZ机制所产生的功率无法拟合表中样本的高喷流功率值,即使当中心黑洞为极端Kerr黑洞时(旋转参数a∗=0.99);2)如果取恰当的参数值,本文的吸积盘热冕喷流加速模型能拟合所有射电源的喷流功率值.计算结果表明,当取无力矩边界条件(∆ε=0)时(见图5中点线),模型喷流功率只能拟合样本中较低功率中的三个,而当参数∆ε取值大于0.5时(见图5中点划线),模型的喷流功率值肯定能高于观测样本的功率值.

5 结论与展望

本文主要讨论了一种从旋转黑洞的吸积盘热冕系统中提取能量的喷流模型.首先求出了热冕中的磁场强度,再利用黑洞磁层理论中的等效电路方法推导出了喷流功率Qjet的表达式.在以往的研究中常忽略黑洞视界面和吸积盘内边缘间的吸入区,本文为了提高模型喷流的功率,考虑了吸入区与吸积盘的磁联系,该磁场在黑洞吸积盘内边缘施加一个磁力矩,磁力矩会大大增加盘冕系统释放的能量.这样本文的模型中的磁能密度和大尺度磁场的强度都将被明显增强,进而提升了盘冕的喷流功率.结果表明,模型喷流功率值主要由吸积率≃Lbol/LEdd、内边缘力矩参数∆ε及黑洞旋转参数a∗决定,并且随着磁力矩参数∆ε和黑洞自转参数a∗的增加而明显增大.

在观测拟合部分,选用了一组具有高喷流功率的天文样本来探讨它们的喷流产生机制,结果表明喷流加速机制在取恰当的参数时可以很好地拟合所有高功率喷流,而这些高功率样本是当吸积盘热冕系统取无力矩边界条件(∆ε=0)或 BZ机制所无法解释的.

当然,本文模型在理论上还存在很多不确定因素和不足之处.比如一个主要不确定因素是系统中热冕的几何结构,在前人的工作中提出了有代表性的冕模型,比如球形冕、平板冕、补丁冕等[36].在本文中为方便计算和研究采用的是一种较简单的平板冕结构,这也是我们以后工作中需要改进的地方.我们也应该注意到由于活动星系核的种类众多,本文提出的喷流模型仅是对部分具有较高功率喷流天体的加速机制的有益探索.

另外,在本文中我们主要讨论了射电喷流的加速机制,并没有讨论吸积盘和喷流两者之间相互影响,这也是一个无可回避的问题.在接下来的工作中,我们将进一步讨论致密天体中射电喷流与吸积之间的耦合关系.

[1]LivioM,Ogilvie G I,Pringle J E 1999Astrophys.J.512 100

[2]Meier D L 1999Astrophys.J.522 753

[3]Lovelace R V E 1976Nature262 649

[4]Bland ford R D,Zna jek R L 1977Mon.Not.R.Astron.Soc.179 433

[5]Bland ford R D,Payne D G 1982Mon.Not.R.Astron.Soc.199 883

[6]Proga D,Stone J M,D rewJ E 1998Mon.Not.R.Astron.Soc.295 595

[7]Meier D L 2001Astrophys.J.548 L9

[8]Macdonald D,Thorne KS 1982Mon.Not.R.Astron.Soc.198 345

[9]Romanova MM,Ustyugova G V,Koldoba AV 1998Astrophys.J.500 703

[10]Tou t C A,Pringle J E 1996Mon.Not.R.Astron.Soc.281 219

[11]Narayan R,Y i I1995Astrophys.J.444 231

[12]Narayan R,Y i I1995Astrophys.J.452 710

[13]Merloni A,Fabian AC 2002Mon.Not.R.Astron.Soc.332 165

[14]CaoX W 2003Astrophys.J.599 147

[15]CaoX W,Rawlings S 2004Mon.Not.R.Astron.Soc.349 1419

[16]CaoX W 2004Astrophys.J.613 716

[17]W illott C J,Rawlings S,Blundell KM,Lacy M1999Mon.Not.R.Astron.Soc.309 1017

[18]Allen S W,Dunn R J H,Fabian AC,Tay lor,G B,Reynolds C S 2006Mon.Not.R.Astron.Soc.372 21

[19]McNamara B,Rohanizadegan M,Nu lsen P 2011Astrophys.J.727 39

[20]Zhang J,Sun X N,Liang E W,Lu R J,Lu Y,Zhang S N 2014Astrophys.J.788 104

[21]Ghisellini G,TavecchioF,Chirlanda G 2009Mon.Not.R.Astron.Soc.399 2041

[22]Ghisellini G,TavecchioF,Foschini L,Chirlanda G,Maraschi L,Celotti A2010Mon.Not.R.Astron.Soc.402 497

[23]Gong X L,Li L X,Ma R Y 2012Mon.Not.R.Astron.Soc.420 1415

[24]Gong X L,Li L X 2012Sci.Chin.Phys.Mech.Astron.55 880

[25]CaoX W 2009Mon.Not.R.Astron.Soc.394 207

[26]Novikov ID,Thorne KS 1973Astrophysics of Black Holes(NewYork:Gordon and Breach)

[27]Page D N,Thorne KS 1974Astrophys.J.191 499

[28]Agol E,Krolik J H2000Astrophys.J.528 161

[29]Zdziarski AA,Lubinski P,Smith D A1999Mon.Not.R.Astron.Soc.303 L11

[30]Gong X L,W ang D X,Ye Y C 2004Chin.Phys.Lett.21 1861

[31]Gong X L,W ang D X 2005Chin.Phys.Lett.22 1293

[32]Gong X L,Jiang Z X 2014Chin.Phys.Lett.31 089801

[33]Thorne KS,Price R H,Macdonald D A1986Black Holes:the Membrane Paradigm(NewHaven:Yale University Press)

[34]Biretta J A,Junor W,LivioM2002NewAstron.Rev.46 239

[35]Moderski R,Sikora M,Lasota J P 1997On Black Hole Spins and Dichotomyof Quasars(Krakow:Jagiellonian University Press)

[36]Merloni A,Fabian AC 2001Mon.Not.R.Astron.Soc.328 958

PACS:97.10.Gz,98.38.Fs,96.60.P–DOI:10.7498/aps.66.039701

Ajet acceleration mechan ismfor the b lack hole d isk system∗

Xu Jia-Di1)Jiang Zhi-Xiong1)Gong Xiao-Long1)2)†

1)(School of Physical and Optoelectronic,Yangtze University,Jingzhou 434023,China)2)(Department of Astronomy,Beijing Normal University,Beijing 100875,China)(Received 22 August 2016;revised manuscript received 25 September 2016)

Ajet accelerationmechanismofextracting energy fromthe disk-corona surrounding a rotating black hole isproposed.In this disk-corona scenario,the central ob ject is a rotating Kerr b lack hole,and a geometrically thin and optically thick disk issandwiched by a slab corona.The large-scaledmagnetic field playsan important role in jet accelerationmechanism.Sowe obtain the value of themagnetic field in such a disk-corona systemby solving the disk dynamic equations in the context of general relativity.The results showthat the value ofmagnetic field decreaseswith the increase of disk radius,while increases with the increase of black hole spin parameter a∗.Then the analytical expression of the jet power is derived based on the electronic circuit theory of themagnetosphere.It is found that the jet power increases obviously with increasing black hole spin parameter a∗and magnetic stress parameter ∆ε.Furthermore,the calcu lation results alsoshowthat the jet power ismainly fromthe inner region of the disk-corona system,which is consistent with the observations of the jet.Finally,a sample composed of the 23 Fermiblazarswith high jet power is used toexplore our jet production mechanism.The conclusion suggests that our jet acceleration mechanismcan simulate all sourceswith high power jet.By comparing with the observational data,we find that these high jet power sources cannot be explained by the Bland ford-Znajek mechanism,even if the central ob ject is extreme Kerr black hole.

accretion,accretion disks,jets,corona

10.7498/aps.66.039701

∗国家自然科学基金(批准号:U1431101,11403003)和国家重点基础研究发展计划(批准号:2012CB821804)资助的课题.

†通信作者.E-mail:x lgong@yangtzeu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.U1431101,11403003)and the National Basic Research Programof China(G rant No.2012CB821804).

†Corresponding author.E-mail:xlgong@yangtzeu.edu.cn