基于支持向量机高校考试测量理论的新方法

宋思雨， 袁 明， 佟 晴， 王美侠， 祝丹梅

(辽宁石油化工大学 理学院，辽宁 抚顺 113001)



基于支持向量机高校考试测量理论的新方法

宋思雨， 袁 明， 佟 晴， 王美侠， 祝丹梅

(辽宁石油化工大学 理学院，辽宁 抚顺 113001)

高校考试测量对选拔人才十分重要，试卷中隐性知识的量化是选拔创新性人才的关键。首先以传统的统计方法对考试结果进行分析，然后在此基础上采用支持向量机方法，通过引入多项式核函数、径向基核函数以及兼具二者优势的组合核函数训练支持向量机，并以不同因子针对显隐性知识的量化进行比较分析，得出不同的分类结果。实验结果表明，考试测量结果的合理评价需基于显性、隐性知识分析，将组合核函数应用于考试测量的优劣是行之有效的方法。

考试测量； 隐性知识； 支持向量机； 组合核函数

近几年来，我国普通高校毕业生规模持续大幅度增长，各单位对选拔人才的标准越来越高，其中学生的学业成绩是其选拔新进人才的重要依据。所以高校课程考试质量的优劣程度对社会的发展至关重要。

当前，各大高校都针对本校发展方向及其特点，制定了相对应的考试测量体系，其中相应的测量法则即相应的测量依据和准则至关重要。使用好的法则可以得到比较理想的测量结果，而较差的法则只能导致不准确的测量结果。但大多数的考试测量体系均是根据教师们的主观意识和经验去命题和评分，编制的试卷并没有经过科学细致的分析，因此无法得到具有科学依据的测量结果，影响成绩评定的公正性[1]。现今考试测量系统中，主要是针对显性知识的评判，通过传统的数理统计方法中信度、效度、区分度、难度等的求解分析，得出评判结果。但随着我国对创新性人才的培养力度加大，考试中的隐性知识显得尤为重要。传统的统计方法有明显的不足，缺少对隐性知识的有效评判。经过调查分析得出3种原因:

(1)缺少针对性，大多数的考试测量系统只是用传统的数理统计方法对考试后的成绩进行局限的分析，并不考虑学科的实际情况，忽略了学科特点。

(2)不进行深度的数据挖掘，大量的成绩数据库中往往存在一些能说明问题并且对学习者有用模式的原始数据，不进行深度的数据挖掘这些数据很难被发现，也就不会产生基于数据挖掘的试题决策支持系统，更无法得到具有科学依据的测量结果[2]。

(3)忽视试题中隐性知识的测量，公正性欠缺。考试测量作为社会选拔人才的标准之一，为得到更公正的测量方式，考试测量系统在模型构建思想、测量工具选择及体系结构完备等方面都必须有所尝试和创新。

因此，本文在传统的统计分析方法的基础上，引入基于组合核函数的支持向量机(Support Vector Machine，SVM)方法。

1 显性、隐性知识

根据知识能否清晰地表述和有效地转移，可以把知识分为显性知识(Explicit Knowledge)和隐性知识(Tacit Knowledge)。隐性知识是M.Polanyi于1958年在哲学领域提出的概念。M.Polanyi认为：“人类的知识有两种。通常被描述为知识的，即以书面文字、图表和数学公式加以表述的，只是知识的一种类型；而未被表述的知识，像我们在做某事的行动中所拥有的知识，是另一种类型的知识。” M.Polanyi把前者称为显性知识，而将后者称为隐性知识。隐性知识本质的特性是默会性，它很难进行语言表述与逻辑说明，隐藏在人的内心，是人的一种特殊“个性”，人的任何表现形式必须依赖于被默会地理解和运用，可以说显性知识往往依赖于隐性知识。隐性知识在人们的学习生活中必不可少，发掘隐性知识是社会快速发展的关键[3]。

2 支持向量机与核函数

支持向量机(SVM)理论[4]是20世纪90年代由C. Cortes等提出的一种新的数据挖掘方法，它以统计学习为基础，以结构风险最小化为原则，在解决小样本、非线性和高维模式识别问题中表现出许多特有的优势。SVM适合于解决二分类模式识别问题，并在模式识别、文本分类、恶意代码检测、医疗诊断、回归估计和天气预报等方面有着广泛的应用，与传统机器学习算法相当[5-10]。SVM可归结为解决一个二次规划问题。在给定空间中输入1个训练样本：

(1)

式中，xi为样本集；yi为类别标号。

得到决策函数：

(2)

式中，k(xi,xj)为核函数；αi为拉格朗日乘子；b为阈值。

引入核函数，相应的二次规划函数表达式为：

(3)

(4)

由于核函数的选取对于SVM是至关重要的，本文采用以下两种核函数。

反向传播算法（BP算法）与人工神经网络（ANN）相结合，就产生了BP神经网络算法。它由输入层、中间层（隐含层）和输出层构成，隐含层可以有一层或多层，每层可以由若干神经元构成。在网络学习训练的过程中，输出值与期望值的误差进行反向传播，直到第一层隐含层，即最靠近输入层的隐含层为止，在反向传播的过程中，对神经元间的连接权重进行调整。BP神经网络结构图如图2所示。

(1)多项式(poly)核函数：

(5)

式中，kpoly(xi,yj)为多项式核函数；d为多项式核函数的幂指数；C为常数。

(2)径向基(RBF)核函数:

(6)

式中，kRBF(xi,yj)为径向基核函数；σ为径向基核函数的宽度系数。

组合核函数能兼顾两个单核函数的优点。两个符合Mercer定理的条件的核函数之和，如果还符合该定理，就可以作为组合核函数。本文采用以上两种核函数构造新的组合核函数k(xi,yj)，其表达式为：

(7)

式中，k(xi,yj)为组合核函数；ρ为调节参数。

3 统计方法数值计算

3.1 统计方法

高质量的试卷不仅能选拔出更具创新能力的人才，还能给学生成绩的排名带来公正性。本文首先以传统的统计方法对某专业12个班级的学生某科目的成绩进行统计分析，得出相关因子，即信度、效度、难度、区分度、平均分、标准差、及格率和优秀率等数据。已知考试测量中难度、区分度是首要的测量标准。本文算法也以难度和区分度作为主要考量指标，其他相关因子为辅助考量指标进行分析，比较分析传统的统计分析方法能否对一次考试进行合理的测量[11]。

表1 各题平均分及其评价

各题效度及其评价如表2所示。

表2 各题效度及其评价

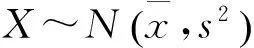
其中，ui为样本值个数；n为样本容量；pi为概率。故可知，在显著性水平α=0.05上，拒绝原假设，表明本次成绩分布与理论上具有相同容量，平均值和标准差的正态分布有显著差异，由此也可说明传统的统计方法并不能很好地对一次考试进行测量，而得出相对满意的结果。

3.2 支持向量机的计算结果

试卷中，主观题往往包含着很多隐性知识，与客观题有较大差异性，根据这点，分别对客观题和主观题进行考试测量。难度和区分度作为测量标准， 分别引入两种核函数及组合核函数比较分析，对考试进行合理评价。实验过程如下：数据集1首先分析客观题难易度，6个辅助因子分别是最高分、最低分、平均分、标准差、高分组正答率及低分组正答率。任取5个班成绩训练，1个班成绩测试。数据预处理为：难易度处于0.300到0.700之间的为+1类，其他的为-1类；数据集2分析主观题难易度，分析过程同数据集1的分析过程；数据集3分析客观题区分度，在数据集1的基础上再增加难易度作为一个因子，分析过程同数据集1。数据预处理为：区分度大于 0.25 为+1类，其他的为-1类；数据集4分析主观题的区分度，分析过程同数据集3。核函数参数选取中，kploy(x，y)的C取1，d取2。实验结果表明，当d=2时，多项式(poly)核函数的外推能力较好。对于kRBF(x，y)，当σ2=0.05时，学习能力强。根据经验和实验，组合核函数中取ρ=0.1，惩罚系数M=10[12-15]。分类结果如表3所示。

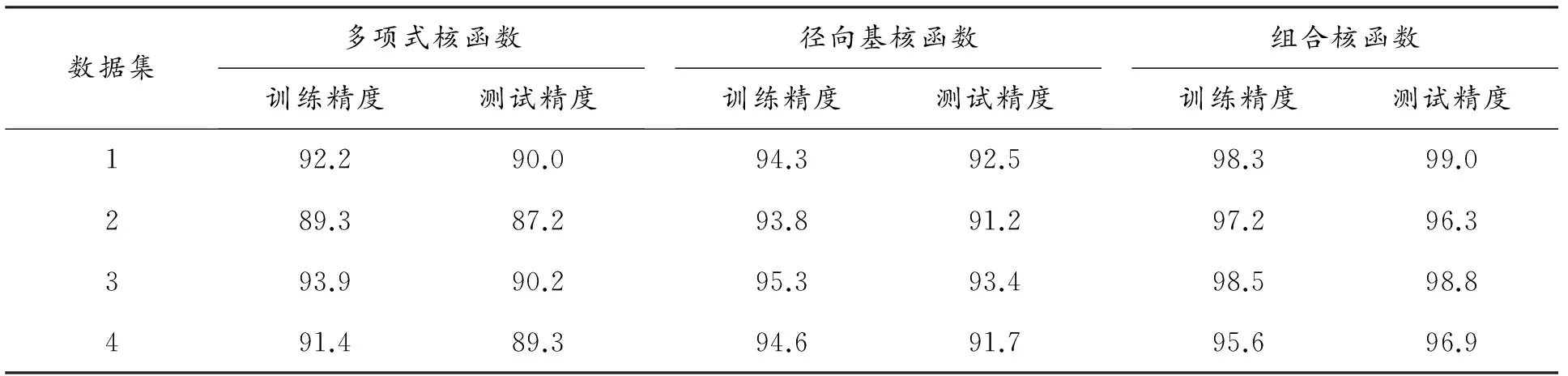
表3 分类结果

从表3可以看出:

(1)在每种核函数下，数据集1较数据集2的计算数值大，数据集3较数据集4的计算数值大，说明在试卷难易度和区分度影响因子条件下，客观题的训练精度和测试精度数值均比主观题要高，表明在考试质量评价中由于主观题所含隐性知识比较多，因此应考虑更多影响因素。

(2)比较3种核函数的计算数值，组合核函数的主观题和客观题的训练精度和测试精度较多项式核函数和径向基核函数计算数值高，比较传统的统计测量方法，使用组合核函数计算的支持向量机方法所得结果相对合理，更能体现高校考试测量的优劣程度，能给我国创新性人才的选拔提供较合理的方法，具有一定的意义[16]。

4 结束语

教育测量理论的创新将是一个有重要意义的研究方向，隐性知识的量化是选拔创新性人才的关键。依据Mercer定理构造了一种新的组合核函数，并分别研究了多项式核函数和径向基核函数，以及将两种核函数组合后的组合核函数应用于考试测量理论。计算结果表明，新的组合核函数在考试测量中能在隐性知识挖掘方面得到更高效的测量结果。由于核参数的选择会影响SVM的性能，在以后的工作中，会对核参数的选取进行更深一步的研究。

[1] 胡中锋，李方.教育测量与评价[M].上海：华东师范大学出版社，2002：3.

[2] 杨志明.题库建设之统计与测量分析系统[J].教育测量与评价，2016(3):4-6.

[3] 郁振华.人类知识的默会维度[M].北京：北京大学出版社，2012：45-47.

[4] 埃塞姆·阿培丁.机器学习导论[M]．范明，等译.北京：机械工业出版社，2015：206.

[5] Haddoud M，Mokhtari A，Lecroq T，et al. Combining supervised term-weighting metrics for SVM text classification with extended term representation[J]. Knowledge and Information Systems, 2016, 49(3):909-931.

[6] Liu X，Lai K K. Intraday volume percentages forecasting using a dynamic SVM-based approach[J]. Journal of Systems Science & Complexity，2016，30(2):1-13.

[7] Narra U，Troia F D，Corrado V A，et al. Clustering versus SVM for malware detection[J]. Journal of Computer Virology and Hacking Techniques, 2016, 12(4):213-224.

[8] 杨旭，纪玉波，田雪. 基于遗传算法的SVM参数选取[J].辽宁石油化工大学学报，2004，24(1):54-58.

[9] 常文文，王宏，化成诚. 基于听觉ERP功能脑网络特征和SVM的测谎方法研究[J].电子学报，2016，44(7):1757-1762.

[10] 郑尧军，陈红岩，冯勇，等. 粒子群优化SVM在气体定量分析中的应用[J].传感技术学报，2016，29(7):1121-1126.

[11] 戴惠荣.基于SPSS17.0的试卷科学性测度[J].科教导刊，2013(26):165-166.

[12] 肖建，于龙，白裔峰. 支持向量回归中核函数和超参数选择方法综述[J].西南交通大学学报，2008，43(3):297-303.

[13] 张春艳，倪世宏，查翔. 一种基于近邻边界的粒度支持向量机学习策略[J].计算机科学，2016，43(3):271-274.

[14] 周志官，郭韵，李渴望. 改进核函数的支持向量机智能诊断方法研究[J].轻工机械，2016，34(5):23-26.

[15] 武剑平.基于BP神经网络的学生高考成绩预测[J].科技传播，2015(20):164-165.

[16] 程双江，李世平，邬肖敏，等.基于改进混合核SVM的非线性组合预测[J].计量技术，2015(10):3-7.

(编辑 陈 雷)

A New Method of College Testing Measurement Theory Based on SVM

Song Siyu， Yuan Ming， Tong Qing， Wang Meixia， Zhu Danmei

(CollegeofSciences，LiaoningShihuaUniversity，FushunLiaoning113001，China)

College testing measurement is very important to choose talent. The quantification of tacit knowledge in test paper is the key to choose innovative talents. First of all, the traditional statistical methods are used to analyze the test results,and then to use support vector machine (SVM) method on the basis of it. It is concluded that the classification of different effects with the introduction of polynomial kernel function，radial basis kernel functions and takes both advantages of combined SVM kernel function training. and with different factors to show the quantitative comparative analysis of tacit knowledge. The experimental results show that the test results of evaluation should be based on the analysis of explicit and implicit knowledge analysis. Reasonable combination kernel function is applied to the pros and cons of the examination measurement is effective method.

Measurement examination； Tacit knowledge； SVM； Combination kernel function

1672-6952(2017)04-0057-04

2017-03-10

2017-04-09

2016年国家级大学生创新创业项目(201610148061);辽宁省教育厅科学研究项目(L2015309);辽宁省本科教改项目(20160193)。

宋思雨(1995-)，女，本科生，数学与应用数学专业；E-mail：290076073@qq.com。

祝丹梅(1972-)，女，博士，副教授，从事数据挖掘、决策优化方面研究；E-mail：zhudanmei@126.com。

G434

A

10.3969/j.issn.1672-6952.2017.04.013

投稿网址：http://journal.lnpu.edu.cn