大型滚动轴承承载特性与滑差演变规律研究*

李军宁，陈 渭，马志涛，杜虎兵

(1.西安工业大学 机电工程学院，西安 710021；2.西安交通大学 现代设计及转子轴承系统教育部重点实验室，西安 710049)



大型滚动轴承承载特性与滑差演变规律研究*

李军宁1，2，陈 渭2，马志涛1，杜虎兵1

(1.西安工业大学 机电工程学院，西安 710021；2.西安交通大学 现代设计及转子轴承系统教育部重点实验室，西安 710049)

以往打滑分析大多侧重对超高转速极轻载荷工况中的滚动轴承进行分析，此处重点针对相对转速较低而载荷较高的大型滚动轴承打滑机理进行研究。以风电轴承为例，构建了轴承承载特性与滑差分析理论模型，研究了径向游隙、滚子有效长度、滚子数对滚动轴承内部接触载荷分布的影响规律，结果表明径向游隙和滚子数对滚动轴承最大承载滚子接触载荷的影响相比滚子有效长度而言更为显著。在载荷分布特性研究的基础上，基于正交试验法系统研究了径向载荷、内圈转速、滚子直径、径向游隙、润滑油黏度等不同因素对轴承滑差演变的影响权重及其影响机理，研究发现各种滑差组合参数对轴承滑差生成与演变影响权重不同，其中径向载荷对滑差影响最为显著。

风力发电机；滚动轴承；打滑；正交试验

0 引言

近年来我国致力于改善诸如沙尘暴、雾霾等为代表的严重环境污染问题，为减少二氧化碳排放量以改善空气质量、实现能源多样化及确保能源安全等原因，包括风电在内的可再生清洁能源发展迅速[1]。风力发电机组中齿轮箱是其关键部件，齿轮箱技术发展的一个重要方向就是结构紧凑和高可靠性运转，这就对齿轮箱中的轴承提出更高的要求[2]。风电行业主机的工况变化差异很大，当齿轮箱面临载荷、速度突变或润滑不良等工况时，轴承极易存在打滑损伤的风险[3]。针对滚动轴承运行过程中出现的打滑失效问题，国内外许多研究者进行了一系列的研究工作。其中，Dowson 等人首先提出了向心圆柱滚子轴承的弹流润滑模型，分析了作用于滚子上的牵引力和切向动压力以及油膜厚度大小[4]。此后，以Dowson 的工作为基础，Harris分析了高速滚子轴承中的打滑情况，发现在高速滚子轴承中增加径向预载可以防止打滑[5-6]。其后，Poplawski 建立了一种考虑滚道接触表面全膜润滑的滚子轴承模型，用于评估给定轴承尺寸参数与运行参数下的保持架滑差率、滚子滑差率、油膜厚度及保持架受力情况[7]。陈国定[8]，王黎钦[9-10]，邓四二[11]，邵毅敏[12-14]，本课题组[15-17]等对影响滚动轴承打滑的因素均进行了一定的研究。已有研究大多集中于通过构建拟动力学模型进行高速滚动轴承的打滑分析上，基于各种假设条件获得多种工况条件下高速滚动轴承的滑差率。

和以往航空发动机等应用中极高转速所导致的轴承打滑失效不同，风力发电机轴承运转转速相对较低，但由于其较大的轴承尺寸使得其具有相对较高的DN值(轴承直径(mm)与轴承转速(r/min)的乘积)，因此其打滑失效问题同样值得关注。目前针对以风力发电机轴承为代表的大尺寸相对转速较低的轴承打滑问题并未得到更多的关注，因此本文重点针对风力发电机用大型滚动轴承开展打滑机理分析，以揭示径向载荷、内圈转速、滚子直径、径向游隙、润滑油黏度等因素对轴承滑差影响权重与影响规律，以及阐明各滑差因素之间的相互作用，进而获得此类轴承打滑失效拟制方法，提高轴承服役性能与寿命。

1 风力发电机轴承承载特性与滑差分析理论模型

1.1 风力发电机传动齿轮箱轴承

传动齿轮箱是风力发电机的关键部件，典型风力发电机传动齿轮箱总体结构如图1所示。在风力发电机传动齿轮箱中，高速轴轴承由于转速较高，并且相比其他轴系轴承而言载荷较轻，加之其较大的轴承尺寸引起的高DN值，因此其极易发生打滑失效。本文主要以风力发电机高速轴轴承NU2334为例，分析滚动轴承内部载荷分布规律，并基于此获取多因素作用下轴承滑差演变规律。

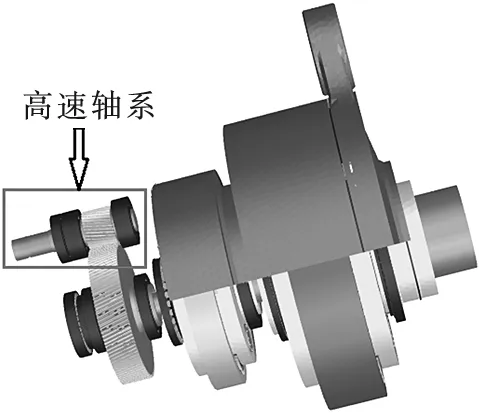
图1 风力发电机传动齿轮箱总体结构图

1.2 理论模型

(1)滚动轴承接触载荷分布

在径向外载荷Fr的作用下，轴承内部载荷分布情况如图2所示。

图2 滚动轴承载荷分布

假定一个滚动体的中心位于径向载荷作用线上，由内圈在外载荷Fr和滚动体负荷Qj作用下的平衡条件，可得：

Fr=Q0+2∑Qφjcosφj

(1)

式中：

Q0—承载最大的滚动体的承载负荷/N；

Qφj—方位角为φj的滚动体上所承受的载荷/N；由变形负荷协调关系可以得出滚动体与滚道接触处的变形量δ与负荷Q之间的关系为：

Q=Kδα

(2)

式中：

K—载荷-变形系数；

α—指数；

假设套圈没有发生弯曲变形，由图2可得，方位角φj处的滚子的弹性变形满足：

δφj=δ0cosφj

(3)

考虑轴承的径向游隙Pd的影响，方位角为φj的滚动体在接触处的弹性变形量可表示为：

(4)

(5)

由式(5)可以得到，当δφj为0时，轴承的承载区域角的半角φl可以确定：

(6)

将式(5)带入式(2)，则：

(7)

将式(7)带入式(1)，则：

(8)

将式(8)转换为积分形式，如下：

(9)

式中：

Jr(ε)—积分参数；

Z—滚动体数目 / 个。

由此，在给定轴承的径向游隙、径向载荷、滚动体数目的情况下，可根据以上公式采用简单迭代法求解得到各滚动体的接触负荷，从而为后续轴承打滑分析提供初始数据[5]。

(2)滚动体运动学模型

以固定滚子为参照物时，轴承的一般运动学关系参见文献[15]。

由滚动轴承内部关系可得，在滚子与内、外滚道接触处的相对滑动速度为：

(10)

(11)

接触点的卷吸速度为：

(12)

(13)

(3)滚动体力学模型[15]

滚动体的受力如图3所示。

(a) 承载区滚子 (b) 非承载区滚子图3 圆柱滚子轴承滚子力学模型

受载滚子的动态平衡方程为：

Qyij+Fω-Qyoj=0

(14)

Fij+Qxij-Qxoj-Foj-Fdj=0

(15)

Fij+Foj=0

(16)

非承载滚子的动态方程为：

Fω-Qyoju=0

(17)

Fdju-Qxoju-Foju=0

(18)

Foju=0

(19)

对整个保持架：

(20)

式中：

Qyij，Qyoj—内、外圈作用于滚子法向压力；

Qxij，Qxoj—内、外圈作用于滚子切向压力；

Fij，Foj—内、外圈油膜作用于滚子的油膜牵曳力；

Fdj—滚子与保持架之间作用力法向分量；

Fω—滚子绕轴承轴线公转所产生的离心力；

u—下标，表示非承载滚子。

接下来对上述方程中相关参数进行无量纲化，基于Newton-Raphson方法通过联立载荷分布计算方程、运动学方程、力学平衡方程等相关方程进行联合求解，通过松弛迭代获得满足预设精度要求的轴承保持架角速度及滑差率等数值结果，进而分析不同参数作用下风力发电机大尺寸滚动轴承的滑差变化规律[15-16]。

2 风力发电机滚动轴承承载特性分析

2.1 分析参数及必要最小径向载荷

主要分析参考数值如表1所示。

表1 主要分析参数

为保证轴承的正常运转，需要满足最小载荷要求，尤其当轴承高速运转或在承受负载方向上处于急加减速状态时。由于滚子和保持架的惯性力、以及润滑剂的摩擦力对轴承的滚动状态将造成不利的影响，极易引起滚子和内外圈滚道之间的滑差失效。和以往经验取值不同，圆柱滚子轴承的必要最小径向载荷与具体型号轴承的尺寸参数、实际转速、额定参考转速、最小载荷系数有关，本文中最小径向载荷Frmin按如下公式计算：

(21)

其中：kr为最小载荷系数，此处取值为0.38。圆柱滚子轴承(NU2334)必要最小径向载荷典型工况取值见表2，表中3400r/min 为NU2334额定极限转速。本文重点研究当轴承载荷小于必要最小径向载荷工况下轴承的承载特性及滑差变化规律。

表2 圆柱滚子轴承(NU2334)必要最小径向载荷

2.2 大型滚动轴承内部载荷分布规律

此处重点研究了径向游隙、滚子数、滚子有效长度对滚动轴承内部接触载荷的影响规律，如图4～图6所示。综合图4～图6可以看出：相比滚子有效长度，径向游隙和滚子数对滚动轴承最大承载滚子接触载荷的影响更为显著。图4表明：最大承载滚子接触载荷随径向游隙的增大而增大，原因在于随着径向游隙的增大，承载滚子数变少且载荷向最大承载滚子集中，因此最大承载滚子接触载荷增大。图5表明：最大承载滚子接触载荷随滚子数的增加而减小，原因在于随着滚子数减少，分担给最大承载滚子的接触载荷变大。图6表明：滚子有效长度对最大承载滚子接触载荷影响较小，原因在于载荷主要从径向方向进行施加，因此沿轴向方向滚子长度变化对最大承载滚子接触载荷影响较小。

图4 最大承载滚子接触载荷与径向游隙关系

图5 最大承载滚子接触载荷与滚子数关系

图6 最大承载滚子接触载荷与滚子有效长度关系

3 多因素作用下风力发电机滚动轴承滑差变化规律研究

3.1 基于正交试验法分析不同滑差因素对轴承滑差演变的影响权重与机理

此处正交试验主要通过16组不同的滑差参数组合，采用四水平五因素L16(45)正交表以研究各滑差因素对轴承滑差影响权重与影响规律。水平因素如表3所示。

表3 正交实验水平因素表

此处结果数据为不同因素组合作用下的保持架滑差率。四水平五因素L16(45)正交表的具体因素组合如表4所示的，极差分析结果见表5。

表4 四水平五因素L16(45)正交表

(22)

(23)

此处KAi是A因素在i水平下的值，Yi是i实验组的实验结果数值，其他K值可以通过类似的方法获得。正交试验分析结果详见表5。

表5 高速滚动轴承滑差影响机理极差分析结果

由表5可以看出，不同的滑差因素对滚动轴承打滑影响权重不同。由极差的大小关系可以得到，径向载荷、径向游隙、内圈转速、滚子直径及润滑油黏度五个因素对滑差结果的影响主次关系是：径向载荷>径向游隙>内圈转速>滚子直径>润滑油黏度。针对风力发电机用大型滚动轴承，径向载荷对轴承打滑失效影响最为显著。针对大多数风力发电机应用而言，由于随机风/载荷的影响，实际加载于滚动轴承上的载荷也存在一定的波动，因此需要合理优化主机结构或选择高性能的滚动轴承以减轻可能出现的打滑乃至失效状况。相比而言，滚子直径和润滑油黏度对风力发电机轴承打滑失效影响较小，原因在于风力发电机转速较低且变化范围较窄，因此黏度对润滑油的润滑与动力性能影响有限，因而对轴承打滑影响较小。对于大型圆柱滚子轴承而言，滚子的尺寸变化效应相对于较大的轴承整体尺寸而言比值较小，因此其对滚动轴承打滑影响较小。

3.2 内圈转速与径向载荷因素对轴承打滑影响

从图7可以看出，针对风力发电机大型滚动轴承而言，随径向载荷增大，轴承打滑情况减轻。当临近或超过轴承必要最小径向载荷时，轴承滑差率数值变小，对于内圈转速600、1200、1800r/min当处于最小必要径向载荷时，滑差率均处于20%以下，且随着径向载荷的增大，这一数值持续减小；而当实际径向载荷由于启、停过程及快速加、减速等极端工况导致低于最小必要径向载荷时，图中可以看出滑差率数值很大，表明轴承打滑情况严重。

图7 内圈转速与径向载荷对风机轴承打滑的影响关系

此外，随着内圈转速增加，轴承滑差率数值变大，表明轴承打滑情况随内圈转速增加而加剧。

4 结论

本文以风电轴承为例，构建了轴承承载特性与滑差分析理论模型，分析了径向游隙、滚子有效长度、滚子数对滚动轴承内部接触载荷的影响规律，并在此基础上基于正交试验法研究了径向载荷、内圈转速、滚子直径、径向游隙、润滑油黏度等不同滑差组合参数对轴承滑差演变的影响权重及其影响机理。

(1) 分析了径向游隙、滚子有效长度、滚子数对滚动轴承内部接触载荷的影响规律，发现径向游隙和滚子数对滚动轴承最大承载滚子接触载荷的影响更为显著。最大承载滚子接触载荷随径向游隙的增加而增大，而随滚子数的增加而减小。

(2) 基于正交试验法研究了径向载荷、转速、滚子直径、径向游隙、润滑油黏度对轴承滑差演变的影响权重与影响机理，结果显示不同滑差因素对滚动轴承打滑影响权重依次为径向载荷、径向游隙、内圈转速、滚子直径及润滑油黏度，其中径向载荷对轴承打滑影响最为显著。

(3) 研究了不同径向载荷和内圈转速组合对轴承打滑的影响机理，发现风力发电机大型滚动轴承打滑情况随径向载荷增大而减轻、随内圈转速的增加而加剧，同时也分析了轴承最小必要径向载荷对轴承打滑现象的影响规律。

本文的研究工作可为风力发电机齿轮箱等类似应用场合故障诊断及失效分析提供一定的参考，进而有助于提高风电设计水平与可靠性。

[1] 徐涛，梁伟．第十三届世界风能大会暨第八届(上海)国际风能展览会成功举办[C]．中国农机工业协会风能设备分会风能产业，2014．

[2] 曲弋．MW级风力发电机组关键部件振动分析与故障诊断方法研究[D]．沈阳：沈阳工业大学，2012．

[3] Y Kang, R D Evans, G L Doll. Roller-raceway slip simulations of wind turbine gearbox bearings using dynamic bearing model[C]//STLE/ASME 2010 International Joint Tribology Conference. American Society of Mechanical Engineers, 2010: 407-409.

[4] D Dowson, Higginson GR. Elastohydrodynamic Lubrication[M]. Oxford: Pergamon Press, 1966.

[5] T A Harris. Rolling Bearing Analysis[M]. Second Edition. New York: Wiley, 1966.

[6] T A Harris. An Analytical Method to Predict Skidding in High Speed Roller Bearings[J]. ASLE Transactions, 1966, 9(3): 229-241.

[7] J V Poplawski. Slip and Cage Forces in a High-Speed Roller Bearing[J]. Journal of Lubrication Technology, 1972, 94(2): 143-150.

[8] 陈国定，李建华，徐建东,等．高速滚动轴承弹性流体动力润滑分析[J]．航空学报，1994，15(12)：1475-1477．

[9] 崔立，王黎钦，郑德志,等．高速球轴承打滑的临界负荷研究[J]．航空动力学报，2008， 22(11)：1971-1976．

[10] 崔立，王黎钦，郑德志,等．航空发动机高速滚子轴承动态特性分析[J]．航空学报，2008，29(2)：492-498．

[11] 邓四二，顾金芳，崔永存,等．高速圆柱滚子轴承保持架动力学特性分析[J]．航空动力学报，2014，29(1)：207-215．

[12] W Tu, Y Shao, C K Mechefske. An analytical model to investigate skidding in rolling element bearings during acceleration[J]. Journal of mechanical science and technology, 2012, 26(8): 2451-2458.

[13] J Liu, Y Shao, T C Lim. Vibration analysis of ball bearings with a localized defect applying piecewise response function[J]. Mechanism and Machine Theory, 2012, 56: 156-169.

[14] Y Shao, J Liu, J Ye. A new method to model a localized surface defect in a cylindrical roller-bearing dynamic simulation[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2014, 228(2): 140-159.

[15] 张立波．圆柱滚子轴承打滑失效分析[D]．西安：西安交通大学，2009．

[16] J Li, W Chen. Effects of different structure parameters on skidding of high-speed roller bearing considering bearing whirling[J]. Journal of Vibroengineering, 2014,16(2): 748-760.

[17] J Li, W Chen, Y Xie. Experimental study on skid damage of cylindrical roller bearing considering thermal effect[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2015, 228(10): 1036-1046.

(编辑 李秀敏)

找检测仪器，请上

QC检测仪器网

WWW.QCtester.com

微信号：qctest

Research on Load Distribution and Skidding Mechanism of Large Rolling Bearing

LI Jun-ning1,2，CHEN Wei2，MA Zhi-tao1，DU Hu-bing1

(1.School of Mechatronic Engineering, Xi’an Technological University, Xi’an 710021, China；2.Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System,Xi’an Jiaotong University, Xi’an 710049, China)

Skid analysis mainly concentrated on the ultra-high speed and light load rolling bearing in the past. In this paper, the load distribution and skid mechanism of large rolling bearing with relatively low speed and heavy load were studied. The load distribution and skid analysis model of rolling bearing in wind turbine were built, and the bearing load distribution characteristics were analyzed in terms of various factors such as radial clearance, effective length of roller and number of roller, the result showed that radial clearance and number of roller have more significant influence on load distribution than effective length of roller. Based on the orthogonal experiment method, the skidding mechanism were investigated systematically in terms of various factors such as radial load, inner ring speed, roller diameter, radial clearance and lubricant viscosity, the result showed that the radial load has the most significant influence on bearing skid.

wind turbine; rolling bearing; skid; orthogonal experiment

1001-2265(2017)07-0032-05

10.13462/j.cnki.mmtamt.2017.07.008

2017-02-06；

2017-03-13

国家自然科学基金项目(51505361)；陕西省高校科协青年人才托举计划(20160121)；陕西省自然科学基础研究计划(2015JM5190)

李军宁(1985—)，男，陕西咸阳人，西安工业大学讲师，硕士生导师，博士，研究方向为机械系统摩擦学与动力学，(E-mail)junningli@xatu.edu.cn。

TH122;TG506

A