磁强计测高自旋弹丸转速的方法及应用

曹咏弘， 薛凯允， 景永强

(中北大学 理学院， 山西 太原 030051)

磁强计测高自旋弹丸转速的方法及应用

曹咏弘， 薛凯允， 景永强

(中北大学 理学院， 山西 太原 030051)

基于力学原理研究了磁强计在高自旋弹丸一般运动时的输出公式. 在高自旋的特定环境下， 基于合理的假定， 化简了磁强计的输出信号， 研究了基于此信号的半周期确定方法及弹丸转速测试方法， 并进行了实弹测试， 利用小波分析方法处理了测试数据. 依据上述转速测试方法得到的转速曲线和利用陀螺得到的转速曲线是一致的， 说明了本文方法的有效性.

磁强计； 高自旋弹丸； 转速； 半周期； 小波分析

0 引 言

本文主要研究飞行时间很短的高自旋战术弹丸的转速确定问题， 由于高自旋弹丸主要在弹道平面内飞行， 且角速度主要为滚转角速度， 因此可以利用一维传感器近似测量高自旋弹丸的转速， 比如用一个沿弹轴方向的陀螺、 PSD或者PSD阵列等. 由于弹丸飞行时间较短， 可以认为弹丸所飞过的区域内地磁场强度不变， 从而可以利用地磁传感器确定弹丸转速， 目前国内外主要是利用线圈式地磁传感器进行测试弹丸转速的研究. 国内， 闫爱天等[1]基于地磁传感器与微机电系统(MEMS)陀螺仪的姿态测量系统, 以MEMS陀螺仪解算所得的偏航角作为三轴地磁传感器输入， 对传统单点姿态测量方法进行了研究与改进； 顾浩卿等[2]对地磁传感器飞行器转速测量方法进行了分析和研究， 并给出了结论及今后的展望、 应用； 马云建等[3]提出了一种适用于滚转弹药的基于地磁组件的角速度测量方法； 邱荣剑[4]介绍了一种双轴地磁传感器测量弹体滚转姿态的方法， 该测量方法利用地磁传感器随弹体滚转时感应磁场变化产生的正弦输出解算弹体滚转角速率及滚转方向； 常树茂等[5]设计出一种地磁传感器弹丸转数测试系统， 提出了基于地磁传感器弹丸转数实际测试中需要注意的问题及解决这些问题的具体方法； 马国梁[6]研究了磁强计/太阳方位角传感器的组合测姿方法， 通过仿真研究表明磁强计/太阳方位角传感器组合测姿方法能达到较高的测量精度； 王嘉雨等[7]采用三轴磁强计和陀螺组合测姿方案， 对姿态角的输出进行了修正； 杨荣军等[8]提出了一种速率陀螺与磁强计组合的姿态测量方案， 利用最优估计技术获得了滚转弹药姿态信息. 国外， Sang-Hee Yoon等[9]基于线圈研究了一种军用的计转速地磁传感器； Slawomir Tumanski[10]详细论述了感应线圈的理论及在各方面的应用. 目前， 利用磁强计测转速的研究很少， 本文就利用磁强计测高自旋弹丸转速进行研究.

1 磁强计测转速的一般理论

1.1 磁强计的安装方式

本文所采用的姿态测试系统由三轴磁通门式磁强计组成， 三轴的方向分别与弹体坐标系三个坐标轴同向， 该测试系统放置在一个铝合金的弹体内， 如图 1 所示.

图 1 三轴磁强计的安装位置Fig.1 The installation position of three axis magnetometer

图 1 只表示出了Oxz平面内的情况，y轴的方向为垂直纸面向里.

1.2 磁强计输出的数学表达式

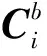
图 2 坐标系之间的转换Fig.2 Transformation between coordinate system

可得磁强计的输出为

式中： {BixBiyBiz}T是当地地磁场的3个分量， 即

Bbx=cψcγBix+(cθsγ+sθsψcγ)Biy+

(sθsγ-cθsψcγ)Biz,

Bby=-cψsγBix+(cθcγ-sθsψsγ)Biy+

Bbz=sψBix-sθcψBiy+cθcψBiz.

由式(3)可以看到， 在一般情况下， 磁强计的输出和3个姿态角都有关系.

2 高自旋时磁强计输出信号的简化

在高自旋的情况下， 根据旋转弹体的飞行姿态变化特点， 一般有如下假定[2，11]：

1) 在标准气象条件下， 弹体偏航角近似不变， 为了下面研究方便， 进一步假定初始偏航角θ=0；

2) 在弹体的一个滚转周期内， 横滚角速率近似不变；

3) 在弹体的一个滚转周期内， 俯仰角基本不变.

2.1 磁强计输出公式的简化[11]

由上述假定偏航角θ≈0， 可以得到sinθ≈0， cosθ≈1， 于是

Bbx=cosψcosγBix+sinγBiy-sinψcosγBiz=

Biysinγ+(cosψBix-sinψBiz)cosγ=

Bby=cosγBiy-cosψsinγBix+sinψsinγBiz=

(sinψBiz-cosψBix)sinγ+Biycosγ=

式(4)～式(6)是在高转速条件下磁强计的近似输出.

2.2 相位信息和转速的关系

研究转速实际上就是关注γ的变化规律， 从式(4)～式(6)看到， 简化后的Bbz和γ没有关系， 而Bbx和Bby都可以看做γ的函数， 所以可以从分析Bbx或Bby中找到γ的变化规律.

以Bbx为例进行分析. 根据假定， 在一个滚转周期内，ψ近似不变， 所以β近似不变， 可以认为Bbx是一条正弦曲线， 但由于在不同滚转周期，ψ在缓慢变化， 因而不同滚转周期内的正弦曲线的幅值在缓慢变化. 利用线圈的输出曲线在一个滚转周期之内是近似正弦曲线这一特征， 可以求出弹丸的滚转周期或半周期. 在一个滚转周期内， 弹丸滚转角近似为360°， 或者说在半个滚转周期内， 弹丸滚转角近似为180°， 由此可以得到转速n为

式中：τ为半个滚转周期， 单位为 s；n的单位为r/s.

连续求出各个滚转半周期内的平均转速， 就可以得到在整个飞行时间内的转速曲线图.

分析Bby同样可以得到滚转半周期及转速.

2.3 基于求极值的半周期的求法

由式(7)可以看到， 求转速的关键是求半周期. 对于正弦波半周期的简单确定方法有两种： 一种是基于零点的半周期求法； 另一种是基于极值的半周期求法， 即通过求波峰波谷的半周期求法. 从后面的实验曲线可以看到， 求零点的方法对于本文来说是不合适的， 因为有些情况并不存在零点， 这里介绍基于极值的半周期求法.

求极值的原理源于高等数学中关于极大值和极小值的定义. 以极大值为例， 一般设函数y=f(x)在x=x0及其附近有定义， 如果f(x0)的值比x0附近所有各点的函数值都大， 就说f(x0) 是函数的一个极大值，x0是极大值点. 换一种理解方式就是在极大值点x0的左边， 差分diff(f(x)) 都是正的， 或者说如果对差分求符号函数的话， 都等于1， 即sign(diff(f(x)))=1； 而在极大值点x0的右边， diff(f(x))<0， sign(diff(f(x)))=-1. 极大值点在出现在diff(sign(diff(f(x))))=2 时； 同理如果是极小值点的话， 就有diff(sign(diff(f(x))))=-2.

通过记录两个相邻的极大值点和极小值点的时间差， 可以得到半周期， 进而可求转速.

3 实 验

3.1 测试设备简介

图 3 所示为三轴磁强计， 在实验中， 为了对以上磁强计测转速的方法进行检验， 增加三轴陀螺(如图4所示)以方便地得到转速， 具体做法是： 首先根据姿态角和角速度之间的微分关系， 由龙格库塔法等求解微分方程的数值方法得到姿态角， 对其中的滚转角微分， 可以得到角速度和转速的关系， 从而得到转速. 转速测试系统的采样频率为 25 kHz， 采样时间为30 s.

图 3 磁强计Fig.3 Magnetometer

图 4 陀螺仪Fig.4 Gyro

3.2 测试数据分析

图 5 是实验测出的一条磁强计的输出曲线.

图 5 磁强计实测数据 Fig.5 Magnetometer’s data

从图 5 可以看到此曲线并不存在零点， 但每个正弦波都存在波峰波谷， 也就是上文中所说的极值， 因而可以利用本文的方法求转速. 数据比较密集的地方表明极值比较密集， 因而转速较高， 数据由密转疏表明转速由大变小.

图 6 磁强计给出的子弹转速图Fig.6 The bullet speed diagram from magnetometer

将数据经小波降噪[12]后， 由上述方法得到的转速是一些离散点， 为了使数据看起来更平滑， 采用样条函数进行数据拟合.

图 6 是拟合后所得到的转速曲线， 从中可以清楚地看到该子弹的转速变化规律： 发射时转速急速增加， 而后转速逐渐变小. 由磁强计的测试数据处理所得的转速曲线和与由陀螺得到的转速曲线(如图 7)变化规律一致， 但具体数据略有些差异， 最大误差小于2%， 完全满足测试要求.

图 7 陀螺仪给出的子弹转速图Fig.7 The bullet speed diagram from Gyro

4 结 论

本文研究了磁强计的一般输出公式， 并研究了在高转速环境下磁强计输出的简化， 以及半周期的确定方法及弹丸转速的测试方法， 并就某一工程问题进行了详细地分析， 利用本文方法得到的转速数据和用陀螺得到转速一致， 最大误差不超过2%， 说明了本文方法的有效性.

[1]闫爱天， 陈雄， 周长省， 等. 基于地磁传感器与陀螺仪的姿态测量法[J]. 弹箭与制导学报， 2016， 36(2)： 143-146. Yan Aitian， Chen Xiong， Zhou Changsheng， et al. Attitude measurement based on magnetometer and MEMS gyroscope[J]. Journal of Projectiles， Rockets， Missiles and Guidance， 2016， 36(2)： 143-146. (in Chinese)

[2]顾浩卿， 陈志， 孟光韦. 地磁传感器飞行器转速测量法研究[J]. 电子测试， 2016(10)： 23-24. Gu Haoqing， Chen Zhi， Meng Guangwei. Geomagnetism sensor’s air rotating frequency testing method research[J]. Electronic Test， 2016(10)： 23-24.(in Chinese)[3]马云建， 辛长范， 贾意弦， 等. 基于地磁传感器测量的滚转弹药角速度估计[J]. 弹箭与制导学报， 2016， 36(1)： 69-72. Ma Yunjian， Xin Changfan， Jia Yixian， et al. Angular velocity estimation of rolling-ammunition based on magnetometer[J]. Journal of Projectiles， Rockets， Missiles and Guidance, 2016， 36(1)： 69-72.(in Chinese)

[4]邱荣剑. 地磁传感器测量弹体滚转姿态方法研究[J]. 兵器装备工程学报， 2014， 35(10)： 103-106. Qiu Rongjian. Research on the method of measuring projectiles roll attitude by geomagnetic sensors[J]. Sichuan Ordnance Journal, 2014， 35(10)： 103-106.(in Chinese)

[5]常树茂， 王利， 弓楠. 基于地磁传感器的弹丸转数测试[J]. 弹箭与制导学报， 2011， 31(5)： 200-201. Chang Shumao， Wang Li， Gong Nan. Projectile spinning speed test based on geomagnetic sensor[J]. Journal of Projectiles， Rockets， Missiles and Guidance, 2011， 31(5)： 200-201.(in Chinese)

[6]马国梁. 高转速弹丸磁强计/太阳方位角传感器组合测姿方法[J]. 南京理工大学学报， 2013， 37(1)： 139-144. Ma Guoliang. Magnetometer/yawsonde integrated attitude measurement for high spin rate projectiles[J]. Journal of Nanjing University of Science and Technology, 2013， 37(1)： 139-144.(in Chinese)

[7]王嘉雨， 曹红松， 白松， 等. 基于自适应滤波算法的磁强计/陀螺组合误差修正[J]. 弹箭与制导学报， 2015， 35(2)： 153-155. Wang Jiayu， Cao Hongsong， Bai Song， et al. Research on integrated error correction of magnetometers and gyroscope using adaptive filtering[J]. Journal of Projectiles， Rockets， Missiles and Guidance, 2015， 35(2)： 153-155.(in Chinese)

[8]杨荣军， 王良明， 修观， 等. 基于磁强计测量的滚转弹药姿态估计[J]. 海军工程大学学报， 2011， 23(5)： 108-112. Yang Rongjun， Wang Liangming， Xiu Guan， et al. Attitude estimation of rolling-munitions using magnetometer[J]. Journal of Naval University of Engineering, 2011， 23(5)： 108-112. (in Chinese)

[9]Yoon S H， Lee S W， Lee Y H, et al. A miniaturized magnetic induction sensor using geomagnetism for turn count of small-caliber amunition[J]. Sensors， 2006， 6(7)： 712-726.

[10]Tumanski S， Induction coil sensors—a review[J]. Measurement Science and Technology, 2007, 18(3)： R31-R46.

[11] 曹咏弘. 基于MIMU 的姿态测试理论及优化算法研究[D]. 太原： 中北大学， 2010.

[12] 胡昌华， 张军波. 基于MATLAB的系统分析与设计—小波分析[M]. 西安： 西安电子科技大学出版社， 1999.

Method and Application of Rotational Speed Test of High Spinning Projectile Based on Magnetometer

CAO Yong-hong， XUE Kai-yun， JING Yong-qiang

(School of Science, North University of China, Taiyuan 030051, China)

Based on the principles of mechanics, the output signal formula of magnetometer was studied in this paper in the case of general movement of the projectile. Then in the case of high-spinning environment, based on reasonable assumptions, the output signal formula of the magnetometer was simplified. And based on the simplified formula, the determination of the half-cycle was studied, and the test method of rotational speed of projectile was studied. The rotational speed curve obtained by the method in this paper is almost same as that obtained by the gyros in the same live-fire test, the result indicates the effectiveness of the method.

magnetometer; high spinning projectile; rotational speed; half-cycle; wavelet analysis

2016-10-08

电子测试技术国家重点实验室基金资助项目(9140C120401080C12)

曹咏弘(1972-)， 男， 副教授， 博士， 主要从事工程力学的研究.

1673-3193(2017)02-0110-04

TP212.13; TJ410.6

A

10.3969/j.issn.1673-3193.2017.02.003