用“巧设值”学数学

万丽芳

我们遇到数量关系比较复杂或头绪比较混乱时，常用设单位“1”来解决分数问题或设未知数后列方程通过大量的计算来解答。有时我们只需要迅速得到结果，可以用设值的方法来达到目的。学数学和语文还是不一样的，语文要求语言丰富，刻画细腻，而数学要求有简洁的方法和正确的结果。设值设得“巧”往往能达到事半功倍的效果，所以我们也要养成用“巧设值”学数学的习惯。

一、用设值来增添条件

我们知道小学数学中最常用的数量关系是：每份数×份数=总数。在应用题中，知道了“每份数”、“份数”、“总数”中两个方面的具体量，第三个方面的具体量就应该可以算出来，不能随便设值。相反，如果只知道其中一个方面的具体量，一般不能算出另外两个方面的具体量，题目就好像“缺”条件，我们可以通过设值出其中另一个方面的具体量，来“增添”条件，达到我们平常的理解。如果设值巧妙，则能迅速地得到结果。

如题目：一批树苗，若分给六年级种，每人种10棵。若分给五年级种，每人种15棵。若分给两个年级共同种，每人种多少棵？

这里只有“每份（人）数”一个方面的具体量，没有“份（人）数”、“总（棵）数”方面的具体量，题目是不可能求出有多少人、总共多少树的。一般的人总觉得缺条件。我们就可以设值：或者设定六年级人数，或者设定总棵数。这里我们可用“公倍数”（通常是最小公倍数或最容易求的公倍数）来设总数比较简单。设定总共有30棵树（[15，10]=30），则六年级有学生：30÷10=3人，五年级有学生30÷15=2人，两年级共有3+2=5人，每人种30÷5=6棵。答案迅速地出来了，但每个年级2人3人的，不合常理，我们就只当是山里小学的复式班啦。

又如：小军从甲地上山到山顶用了90分钟，从山顶下山到乙地用了60分钟。已知他下山速度总是上山速度的2倍。小军从乙地上山经山顶返回甲地需要多长时间？

此题只有“份数（时间）”方面的具体量，没有“每份数（速度）”、“总数（路程）”方面的具体量。同样，我们可以设值来“增添”条件。这里，我们根据倍数关系“小军下山速度是上山速度的2倍”来设定具体值：上山速度每分钟1米，下山速度每分钟2米。于是很容易算出：甲地到山顶路程：1×90=90米；山顶到乙地路程2×60=120米，返回用的时间是120÷1+90÷2=165分钟。同样速度虽然不够合理，但计算简便，我们把小军当成一只小山龟就可以理解了。

虽然说“每份数”、“份数”、“总数”中只有一个具体量时，我们可以设值，但只要我们熟练掌握这个方法，对题中有两个方面的具体量时，我们依然可以借鉴这个方法。如：一次聚餐，每人用一个饭碗，每2人用3个菜碗，每5人用一个汤碗，一共用了540个碗。参加聚餐的一共有多少个人？这题在六年级学了分数除数后可以做，每人用1+3÷2+1÷5=2.7个碗，共有540÷2.7=200人。此题给四、五年级做，我们就可用设值方法了：如果我们先撇开“540个碗”这个“总数”具体量，题目就只有“每份数”这个具体量了。我们可以设人数为10人（[1，2，5]=10），则可以算出共用了10+15+2=27个碗。再把540与27相比，碗是20倍，人数应该是20倍了。10×20=200人。我们只当是10人一桌，共20桌，就好理解了。

二、利用设值来简化关系，理清思路

有些题目故意把数量关系说得很“绕”，像绕口令一样把人绕进去，使人晕头转向，理不出头绪。我们可用设值来简化条件，理清关系。

如：狗和兔同时从A地跑向B地，狗跑3步的距离等于兔跑5步的距离，狗跑2步的时间等于兔跑3步的时间。狗跑840步到达B地时，兔还要跑几步到达B地？

我们设值：狗跑3步距离=兔跑5步距离=15米。

条件简化为：狗每步5米，兔每步3米。

再设值：狗跑2步的时间=兔跑3步的时间=1秒。

条件演化成：狗每秒跑：5×2=10米；兔每秒跑：3×3=9米。

则容易算出：AB两地距离：5×840=4200米。

狗跑完用时：4200÷10=420秒

兔420秒跑的距离：9×420=3780米

兔还差多少米到B地：4200-3780=420米。

换成兔的步数：420÷3=140步

有些分数题目，有很多分数关系，没有具体量时，我们也可以直接进行设置，将分数关系直接轉化成具体量，可以减轻思维难度，迅速得到结果。

如：甲校学生是乙校的40%，甲校女生是甲校学生的30%，乙校男生是乙校学生的42%，两校女生数是两校学生数的百分之几？

此题作为分数应用题可以用单位“1”的方法来解。但为了迅速得出答案，我们采用设值法：根据40%设甲校400人，乙校1000人。则甲校女生400×30%=120人，乙校女生1000×（1-42%）=580人。再用（120+580）÷1400×100%迅速求得两校女生占35%。

有一道奥数题目，看起来很复杂：“有两包糖，各由奶糖、水果糖、巧克力糖组成。第二包糖的颗数是第一包糖的3/4。第一包中奶糖占25%，第二包中水果糖占40%，巧克力糖在第一包中所占的百分比与第二包中所占百分比相等。当两包合在一起时，巧克力糖占30%，水果糖占百分之几？”我们先设值，将题目简化为：“有两包糖，各由奶糖、水果糖、巧克力糖组成。第二包300颗，第一包400颗。第一包中奶糖有100颗，第二包中水果糖有120颗。巧克力糖在第一包中所占的百分比与第二包中所占百分比相等。当两包合在一起时，巧克力糖共210颗，水果糖占百分之几？”再通过画图、比较，是不难做出的。

三、用设值来找到突破口

有些题目，我们乍一看，或者觉得缺条件，或者觉得超出我们的能力范围，其实是没有巧妙的找到突破口。我们可以设特殊值，或者特殊到极点的值（极限）来思考，就可以找到突破口了。

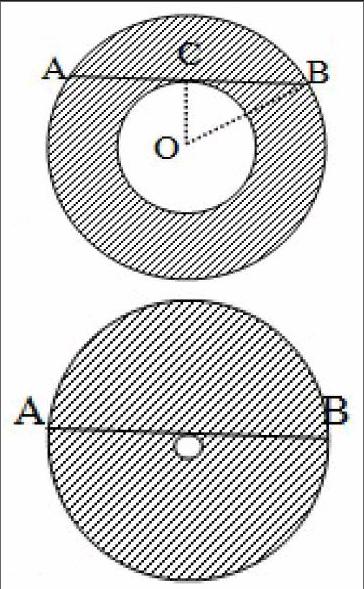
如图一：圆环中，AB=8厘米，要求圆环的面积（即阴影部分的面积）。

这题对于学过勾股定理的初中生来说不是问题，对于只学过圆的面积公式的小学生来说就显得难以下手。学生只想着用大圆面积减去小圆面积，如果知道OC和OB的长度就好算了。因为CB=4，如果学生知道“勾三股四弦五”的故事，能把OC看成3，把OB看成5吗？如果这样做，结果是对的。但又想，如果能把OC设为3，能不能将之设为1，或0.1，或0.01呢？OC的值越接近0，AB的长越接近直径，圆环的面积越接近圆的面积，如图二。

我们现在就设最特殊的值，OC就等于0，那么，AB就是直径，圆环面积就是圆的面积。根据直径求面积，学生能轻松算出。

到了中学，会盛行用字母表示数量关系，我们根据表达式有时判断绝对值，有时判断判别式，有时判断长度、面积、体积等几何值之间的关系，往往要用到设巧妙的特殊值计算，反过来，由具体的典型值去理解抽象的数量关系。

其实，设值方法是不够严格的，它是由个性去推得共性的结果，因此也是需要在一定的条件下才能用的。但这种方法能迅速找到一条路到达目的地，培养了思维的直觉性。在数学探索方面也需要思维的直觉性，数学历史上有很多数学难题：如“化圆为方”、“七桥问题”等，当我们一次次地证明不了的时候，能不能凭直觉感知到是不可能的，再从相反的方向去证明呢？“巧设值”好比大家都在论证能否到金山找到金子的时候，你却自己驾个小渔舟，到金山捡了块金子回来了。这也是异于常人的思维，是创造性思维的表现形式之一。