小学数学乘法分配律教学初探
李剑锋
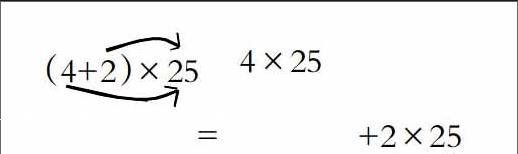
【摘 要】乘法分配律是小学阶段的重要运算定律。乘法分配律因其应用广泛、变化丰富、隐蔽性强、易于混淆等特点,无可争议地成为小学生认知上的难点。在教学中灵活巧妙地运用乘法分配律,不仅能解决教学中的诸多问题,还有利于培养学生的观察比较能力,提高学生的计算能力。
【关键词】小学数学;乘法分配律;教学实践
《课程标准》的基本理念所言:“数学教学活动,特别是课堂教学应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法。”教师在教学中既注重学生算理的理解、算法的掌握,又关注了学生良好习惯的培养,就可以有效地提高教学质量,促进学生运算技能的提高。乘法分配律这个知识点老师难教,学生难学。根据学生的情况,我在教学中采用“巧抓类型,分层把握”的策略,让学生在理解乘法分配律本质和基本类型的基础上建构模型,灵活运用。
一、理解基本类型的“分”掌握乘法分配律的特点
乘法分配律即两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。用字母表示的形式是(a+b)×c=a×c+b×c。这是乘法分配律最基本的类型,其思维方向是从先求和再求积转变为分别求积再求和,形式改变但结果不变。学生要特别注意两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加中的“两个数的和”与“分别”两个字。即一定要括号外的数分别乘括号里的两个数,再把积相加。这就是乘法分配律的“分”。
通过教材例题揭示乘法分配律,初步理解“分别相乘”。首先通过计算发现(4+2)×25与4×25+2×25结果相等;再观察箭头明白“分别相乘”。其次编形象化的语言帮助学生理解乘法分配律中“分别相乘”。“爸爸和妈妈都爱我等于爸爸爱我和妈妈也爱我”。最后深化到乘法分配律的本质。即(4+2)的和个25等于4个25加2个25。
这个基本类型常常应用于几个数的和(或差)与一个数相乘的简便运算中。在这个基础上,引导学生顺向扩展,掌握一些不同的形式乘法分配律基本类型:(a-b)×c=a×c-b×c;(a+b-d)×c=a×c+b×c-d×c。乘法分配律教学,除了因为它的构成因素多,展开式长一点外,更在于应用中的变化类型复雜。教者只有清晰地把握这些变式类型,才能在教学中,左右逢源,化难为易。
笔者根据自身多年教学经验,以一般字母表达式 “(a+b)×c=a×c+b×c”为基本式展开分析,试做如下分类:
1.在乘法分配律中套用乘法交换律的变式。这就是将乘法分配律基本式左边“(a+b)×c”变化为“c×(a+b)”,即需要变化为:c×(a+b)=c×a+c×b。虽然这样的变化是较简单的,但是,对于初学学生来说,还是具有了一定困难性。这需要教者有意识地作出多次安排,并要组织学生进行分辨对比。
2.延展乘法分配律项数的变式。这是顺次增加项数的变化。比如,将c×(a+b)两数和与一个数相乘,变为三四个数的和与一个数相乘。即:(a+b+c)×d=a×d+b×d+c×d。
3.两个数的和变为两个数差的变式。这是在同级运算之间的拓展,比如(a-b)×c=a×c-b×c。例如:(40+8)×25等,通过这些训练,大部分学生都能比较容易地掌握基本类型的简算方法。
二、理解乘法分配律逆推型的“收”,掌握乘法分配律的本质
所谓逆推型,即逆向推收,是乘法分配律的逆向运用。对乘法分配律的逆向性变化,即要让学生既能从左向右思考,也习惯于从右向左逆推。要让学生善于从计算简捷性要求出发,灵活地选择应用乘法分配律展开式的可逆变化方向,是训练学生熟练计算技能的重要途径。从一道式子中两个或三个积之和的形式推收成两个或三个数之和与一个数的积的形式,这是逆向思维的一种类型。“a×c+b×c=(a+b)×c”“a×c-b×c=(a-b)×c”“a×d+b×d+c×d=(a+b+c)×d”。
例如:76×35+76×65=(35+65)×76=100×76=7600。当学生训练完上面例子,接着让学生计算另一算式:24×12-24×2,使学生明白乘法分配律对于减法同样适应,这些方法学生容易掌握。再次要让学生通过大量习题练习发现特点。例 如:练习36×34+36×66等题后,要组织学生思考梳理:(1)一道式子必须是两个或三个积之和(或差)的形式;(2)而且积中还有一个相同的因数。这里要特别让学生观察理解:(3)变式书写时两个积中相同的因数只能写一次,即“收”。一个相同的因数作代表来乘的本质就a个c加b个c等于a加b的和个c或a个c减b个c等于a减b的差个c。为了让学生好理解,可用具体数字来证明即4个25加2个25等于4加2的和个25或4个25减2个25等于4减2的差个25。
在乘法分配律逆推型中尤其让学生反复理解特殊数“1”参与展开的变化式。即a×b+b=a×b+b×1=(a+1?)×b的形式。这里要求学生把一个确定的数,看作是一个算式,是这个数与1的积。例如:83+83×99=83×1+83×99,把83看作83×1,再用乘法分配律逆推类型来简算。
三、理解乘法分配律替代型的“替”掌握乘法分配律的灵魂
所谓替代型,即把接近整十或整百整千的数,用两个数的和或两个数的差来代替。例如:把102看作100+2,81看作80+1,99看作100-1等。78×102=78×(100+2),125×81 =125×(80+1),通过替代,把算式就转化为乘法分配律的基本类型,学生就容易进行简便运算了。
四、强化指导突出“练”,体会乘法分配律的“巧”
1.个别指导。对该定律理解的困难的孩子,要加强个别的指导。具体是举一些相关的实际问题,让孩子用两种不同的方法进行解题,在解题、比较的基础上理解两部分积表示的意义,理解括号外的数要分别乘括号内两个数的道理,这样借助具体事例,形象的进行理解、概括,有助于学生对乘法分配律的掌握。
2.对比练习。针对有的孩子把分配律和结合律混淆的情况,我设计针对性的练习,让孩子在练习中记性比较、分析,从而掌握。如:25×3×17×4,25×3+17×25比较两个算式的不同之处,说说算是中分别有什么运算,运用什么运算律才能简便计算,这样在比较的过程中学生能够慢慢区分乘法结合律与乘法分配律的区别。
3.针对练习。针对学生不能灵活应用规律进行简算的,我设计针对性的练习,让孩子在练习中说说自己的想法,比一比怎么计算更加简便。如:125×88因为刚学过乘法分配律,学生在计算125×88时,也应用分配律:125×80+125×8,针对这样的情况,我让学生再想一想还有没有其它简便计算的方法,引导学生用乘法结合律进行简便计算:125×8×11,再比一比:哪种方法更简便?这样在比较的过程中引导学生体会:用简便方法进行计算时,一定要先观察题目中各个数的特点,根据题目的特点选择合适的运算律进行简便计算,这样才能保证计算的简便与正确。

