罕遇地震下钢混组合结构损伤时变特性
王 莹 王若竹 李兆霞
(1东南大学江苏省工程力学分析重点实验室,南京 210096)(2常州市机关事务管理局,常州 213001)
罕遇地震下钢混组合结构损伤时变特性
王 莹1王若竹2李兆霞1
(1东南大学江苏省工程力学分析重点实验室,南京 210096)(2常州市机关事务管理局,常州 213001)
面向复杂钢混组合结构,依据动力弹塑性时程分析法获得罕遇地震下结构的动力响应,分别利用基于整体法和加权组合法的地震损伤时变模型,研究了罕遇地震下结构的损伤时变特性.考虑到结构刚度和阻尼等参数在计算时必须为常量,而在整个服役期间又具有变量特征,因此将其作为拟变量处理.通过研究一典型钢混组合算例发现:罕遇地震下结构损伤值呈现显著的时变特性,甚至可能超出相应性能限值;刚度变化会引起抗侧向力能力和地震传导能力的改变,使得时变损伤值呈现波动性,其中前者占主导作用.地震作用越大,地震传导能力变化对损伤影响越大,导致时变损伤值波动越显著,结构振动形态也发生显著变化.通过对比服役期内结构时变损伤与不考虑材料时变特性的设计值的差异可以发现,材料的时变特性对于抗震设计和评估的准确性有重要影响.
钢混凝土组合结构;时变损伤;时变特性;动力弹塑性时程分析
型钢混凝土组合构件因其具有良好的抗震性能在复杂高层结构中得到了广泛的应用.在有关建筑抗震性能的研究中,研究人员通常结合此类结构的性能化设计需求,基于数值模拟或实验技术等来探究不同类型的构件在地震作用下的破坏机理,进而对整体结构的承载能力和抗震性能进行评估[1-4].
对地震下结构损伤理论的研究主要集中在能描述损伤的构件层次和结构层次.李晓蕾等[5]基于刚度与能量的双参数地震损伤模型,定量描述了短肢剪力墙损伤破坏的全过程.侯丕吉[6]提出了基于变形和累积耗能非线性组合的型钢高强高性能混凝土框架柱地震损伤模型.Park等[7]将各构件的耗能比作为权重系数,由构件损伤加权得到楼层损伤,再由楼层损伤得到整体结构的损伤.欧进萍等[8]认为结构薄弱层和发生损伤的楼层位置对结构损伤有着重要影响,采用相应的构件损伤重要性指数加权得到整体结构损伤.杜修力等[9]对加权组合法进行了进一步研究,指出损伤越大的楼层对结构损伤的影响越大,通过楼层损伤确立加权系数.蒋欢军等[10]提出了非线性的楼层位置系数,进一步完善了加权组合法损伤模型.
可见,上述研究主要基于各类损伤本构关系,提供了多种从构件到结构的损伤评估方法,但研究多针对钢筋混凝土构件,而对于复杂钢混组合结构的损伤研究较少.对于此类结构,随着性能化设计要求的不断提高,从材料的时变效应来研究构件的时变性能,进而研究对整个结构时变性能的影响越来越得到设计人员和监测人员的重视.因此,本文针对服役期内的复杂钢混组合结构,基于动力弹塑性时程分析法研究罕遇地震下结构的动力响应,以及材料的时变性能对整体结构时变性能的影响,从而评估结构的抗震性能.
1 钢混组合结构时变损伤研究流程
首先,通过改变材料的抗压强度、弹性模量等力学参数来改变结构的刚度和阻尼等参数.由于地震波作用时间相较于服役期是一个极小的时间段,因此将刚度和阻尼作为拟变量处理:即在整个服役期内,刚度存在时变特性,为变量,但在特定的服役时间点进行动力弹塑性时程分析时,将刚度和阻尼作为常量代入.这样既保证了时变特性研究的需要,也便于应用显式的动力弹塑性时程法进行求解.其次,分别采用整体法和加权组合法来获得整体结构的损伤.整体法基于最大的楼层层间位移,而加权组合法根据剪力墙的层间位移、型钢混凝土柱的层间位移、型钢梁的梁端转角、连梁弦转角等关键构件的力学参数,通过选择合理的关键构件的加权系数和楼层的加权系数,综合评估整体结构的损伤.具体的研究流程如图1所示.
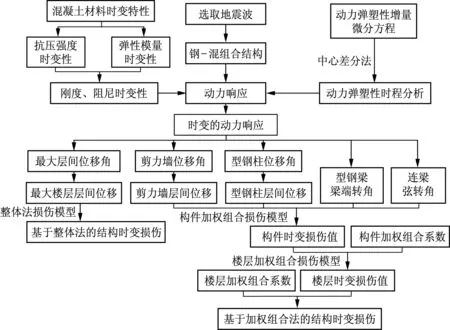
图1 钢混组合结构时变损伤研究流程图
2 混凝土材料时变模型
对于混凝土材料,随着时间变化的力学性能难以通过实验室的加速实验在短期内呈现.目前对混凝土材料强度的主要研究方法有基于现场统计大数据的实测法和实验室模拟环境法等.国内外研究人员基于上述2种方法,建立了一系列考虑时变效应的强度均值的数学模型[11].
文献[12]通过回弹法和钻孔法检测了大量服役期限为1~60年的建筑,收集2 000多组数据进行归一化处理,并采用假设检验和参数估计得出混凝土强度时变的概率分布函数,提出了新的混凝土材料时变强度的非线性模型.该模型能直观反映混凝土强度时变效应对设计误差的影响,适用年限长,因此本文选用该模型作为材料强度的时变分析模型.该模型表达式如下:
fc(t)=fcu,k(-2.861×10-4t2+
1.384×10-2t+0.876 9)
(1)
式中,fc(t)为服役t年时的混凝土强度;fcu,k为混凝土标准抗压强度.
混凝土抗压强度将影响材料的弹性模量,依据文献[13]中两者之间的关系,建立如下时变模型:
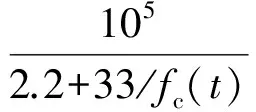
(2)
式中,Et为服役t年时的混凝土弹性模量.
3 基于整体法的地震损伤模型
层间位移角是地震变形中的主要控制参数,也是运用整体法评估结构损伤的重要指标.对于钢混组合结构在地震作用下的层间变形,《建筑抗震设计规范》规定:层间位移限值采用钢筋混凝土结构限值.结合规范对于结构弹塑性阶段的层间位移角的限值及其对应的损伤等级划分和损伤程度描述[14],本文提出基于层间变形和地震损伤等级的多级时变损伤模型:
(3)
式中,Dt为服役t年时的损伤;Δut为结构在服役期t年遭遇地震时的最大层间位移;Δu1,Δu2,Δu3和Δu4分别表示结构在地震作用下达到轻微损伤、中等损伤、严重损伤和倒塌时的层间位移限值.
损伤等级为基本完好对应抗震设防水准一的“小震不坏”的要求;损伤等级为轻微损伤和中等损伤时满足抗震设防水准二的“中震可修”的要求;损伤等级为严重破坏和倒塌时满足抗震设防水准三的“大震不倒”的要求.对界定地震破坏等级的4个层间位移角限值分别定义为θ1,θ2,θ3,θ4,楼层层间位移为各楼层的层间位移角与相应层高的乘积.层间位移与损伤的关系如表1所示.

表1 层间位移和结构损伤值的关系
4 基于加权组合法的地震损伤模型
由于构件的变形往往是其他动力响应改变的基础,在大量包含变形和能量的双参数损伤评估模型中,变形引起的损伤指数一般在80%以上,许多学者通过实验研究构件的变形与承载性能的关系并提出功能指标.因此,本文从复杂钢混组合结构中的钢筋混凝土剪力墙、型钢混凝土框架柱、型钢梁、钢筋混凝土连梁这4类关键构件的承载性能及损伤机理入手,建立了基于变形的加权组合损伤模型.
表2为剪力墙构件在各性能目标下相应的位移角与损伤程度,表3为型钢混凝土柱在各性能目标下相应的位移角与损伤程度.

表2 剪力墙位移角与损伤程度的关系
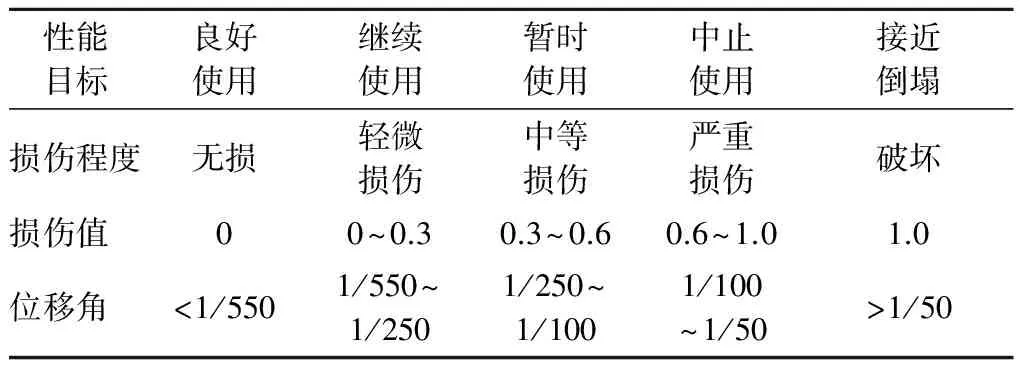
表3 型钢混凝土柱位移角与损伤程度的关系
根据位移角和层间位移的关系,可得剪力墙、型钢混凝土柱在各损伤状态下的层间位移限值,而运用动力弹塑性分析法可获得层间位移等结构响应.根据剪力墙和型钢混凝土柱在服役期内遭遇地震时的结构响应,定义这2类构件的损伤时变模型如下所示:
(4)
式中,下标a,b分别表示剪力墙和型钢混凝土柱;Dat(bt)为服役t年遭遇地震的剪力墙和型钢混凝土柱的时变损伤;Δuat(bt)为服役t年遭遇地震的剪力墙和型钢混凝土柱的最大层间位移;Δua1(b1),Δua2(b2),Δua3(b3)和Δua4(b4)分别为剪力墙和型钢混凝土柱达到轻微损伤、中等损伤、严重损伤和倒塌时的构件层间位移限值.
型钢梁在地震作用下多数保持弹性状态.当结构破坏严重时,主要损伤由底部柱脚屈服造成.根据变形破坏准则结合《结构抗震设计规范》中对于钢框架结构抗震设计的要求,建立梁端部转角与损伤值区间的对应关系,如表4所示.
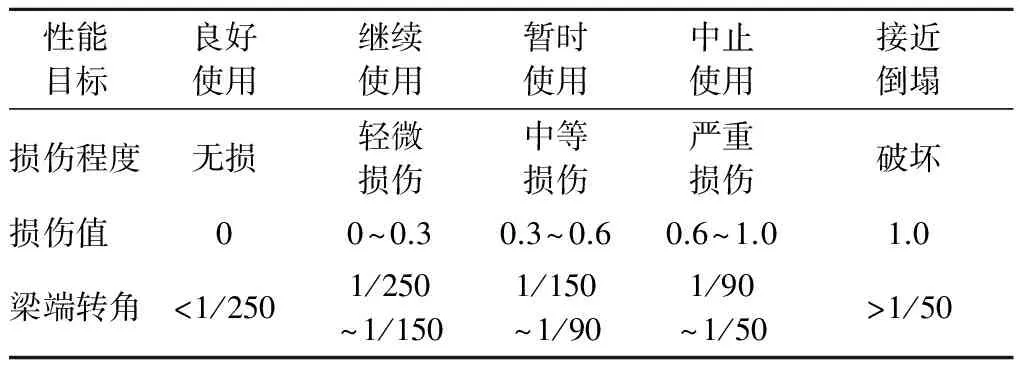
表4 型钢梁梁端转角与损伤程度的关系
本文采用弦转角作为连梁的性能控制指标.弦转角一般指连梁变形后两端的竖向位移与净跨度的比值,其与损伤程度的对比如表5所示.
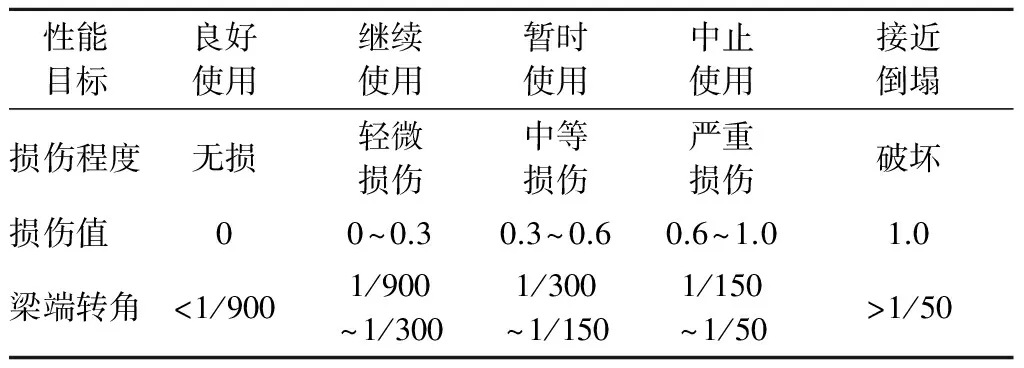
表5 连梁位移角与损伤程度的关系
根据型钢梁和连梁的性能角限值,建立型钢梁和连梁的损伤时变模型:
(5)
式中,下标c,d分别表示型钢梁和连梁;Dct(dt)为服役t年遭遇地震的型钢梁和连梁的时变损伤;θct(dt)为服役t年遭遇地震的各楼层型钢梁的梁端转角和连梁的弦转角的最大值;θc1(d1),θc2(d2),θc3(d3)和θc4(d4)分别为型钢梁和连梁达到轻微损伤、中等损伤、严重损伤和倒塌时的梁端转角和弦转角的限值.
研究发现,损伤越大的构件对于结构损伤的影响越大[15],因此赋予不同构件以不同的加权系数.运用加权组合法得到楼层的损伤时变模型:
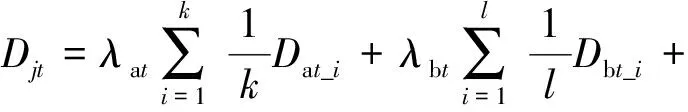
(6)
式中,Djt表示第j层楼层在服役t年时的结构损伤;Dat_i,Dbt_i,Dct_i,Ddt_i分别为服役t年遭遇地震时第i个剪力墙、型钢混凝土柱、型钢梁、连梁的时变损伤值;λat,λbt,λct,λdt分别为上述各类构件在服役t年时的加权组合系数;k,l,m,n分别为相应构件的个数.
不同楼层对结构损伤的影响程度不同,一般而言,底部楼层的影响程度大于上部楼层.文献[10]提出了非线性的楼层重要性系数γj:

(7)
式中,N表示楼层总数.
此外,由于楼层结构分布不同、存在薄弱层等因素,不同楼层对损伤的影响不同,楼层损伤值越大,对整体损伤评估的影响越大,因此本文建立具备时变特性的楼层损伤贡献系数:
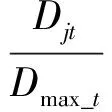
(8)
式中,ωjt表示服役t年时在地震作用下第j层楼的楼层损伤贡献数时变值;Dmax_t表示服役t年时遭遇地震作用的楼层损伤最大值.
结合上述楼层重要性系数和楼层损伤贡献系数,建立如下具备时变特性的整体结构时变损伤模型:
(9)
式中,λj为第j层楼层的损伤加权系数;Dj为第j层的楼层损伤.
5 算例分析
本算例为一高层写字楼,内部为混凝土剪力墙核心筒,外部为工字钢混凝土混合柱和型钢梁组成.结构总高度90 m,20层,层高4.5 m.标准层的平面图及结构示意图如图2所示.抗震设防烈度为8度,设计基本加速度为0.2g,场地类别为Ⅱ类,设计地震分组为第1组,特征周期为0.35 s.本文在计算中未考虑楼板作用,可能导致计算的自振周期比真实结构略大.结构符合《建筑抗震设计规范》的要求,结构的外部框架结构和核心筒结构的抗震等级都为一级,设计使用年限为60年.具体截面尺寸及材料如表6所示.
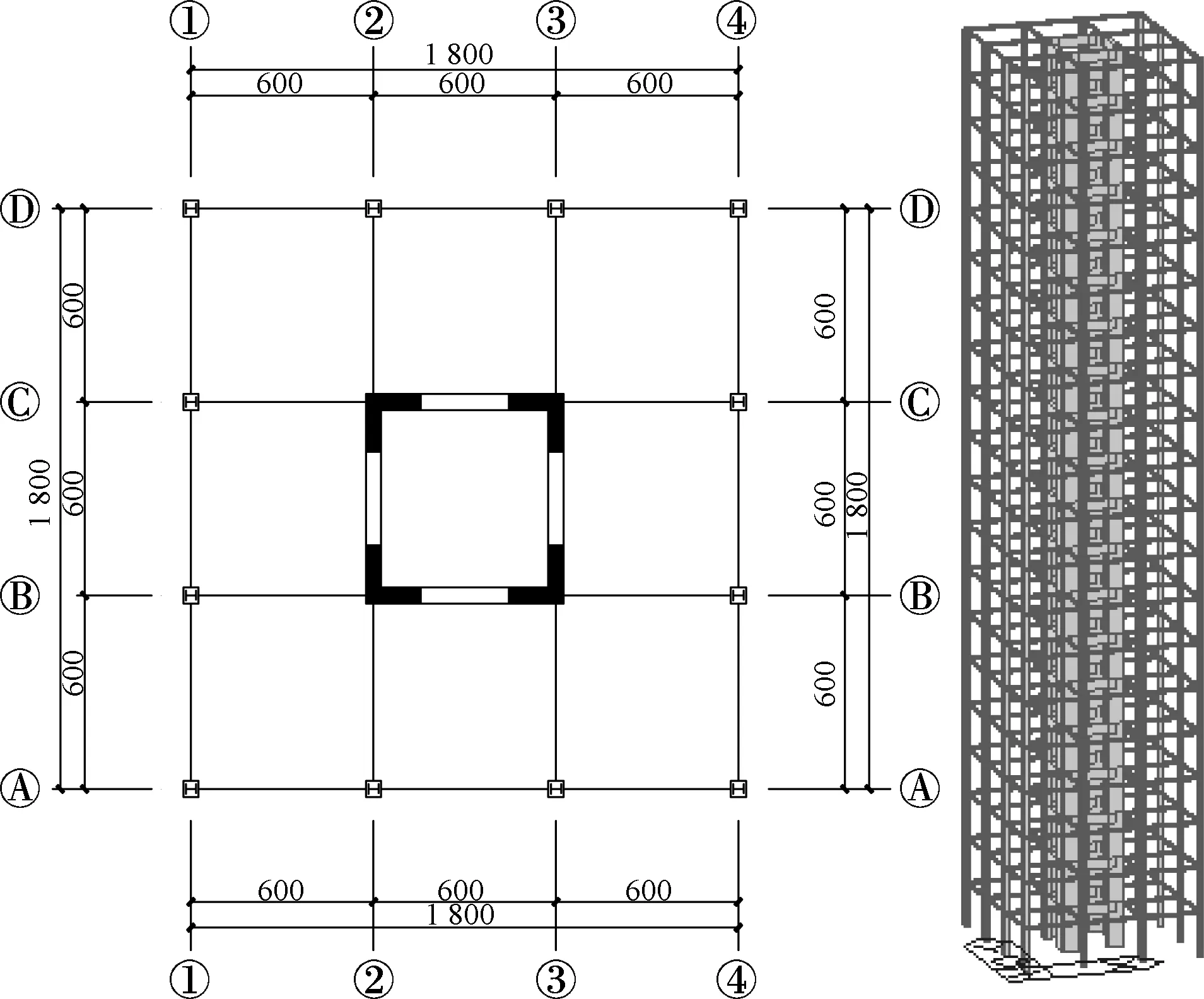
(a) 平面图 (b) 结构示意图

构件主要材料截面尺寸剪力墙C40混凝土1800mm×400mm型钢混凝土柱C40混凝土Q235钢500mm×500mm型钢梁Q235钢250mm×250mm×9mm×14mm连梁C40混凝土1000mm×400mm
采用纤维束模型进行动力弹塑性时程分析,截面的轴向变形和弯曲变形通过每个纤维的轴向变形实现,纤维的应力状态通过纤维的应变状态求解,继而计算截面的弯曲和轴力.纤维束模型如图3所示.本文选用Kent-Scott-Park模型[16]作为混凝土纤维的本构模型,钢材的纤维模型则采用Menegotto-Pinto模型[17].

图3 构件纤维束模型示意图
5.1 地震波选取
建筑规范中对罕遇地震的设防要求为“大震不倒”.表7给出了不同设防等级下的峰值加速度基准值,可按照下式调整地震波幅值以使峰值加速度达到对应的基准值:
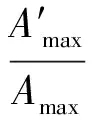
(10)
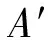
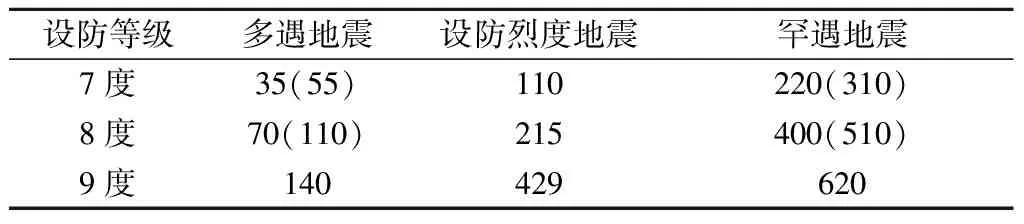
表7 峰值加速度基准值 cm/s2
注:括号内数值用于设计基本加速度为0.15g和0.3g的地区.
选取具有代表性的3条地震波:E1-Centro波、T2-Ⅱ-2波和Northridge波.基于动力弹塑性时程分析方法,获得结构在遭遇罕遇地震时的结构响应,采用整体法损伤模型和加权组合法损伤模型,研究罕遇地震下的结构损伤时变效应.
5.2 基于整体法的结构损伤时变特性研究
结构在服役期内遭遇罕遇和多遇地震(E1-Centro波)的时变损伤如图4所示.从图4(a)可看出,损伤值存在显著的时变特性,在服役前45年,损伤变化呈现明显波动,在服役50~60年遭遇地震时的时变损伤显著大于服役前45年遭遇地震时的损伤值.在多数服役年限,遭遇E1-Centro波作用时的时变损伤,显著高于不考虑材料时变特性时的结构损伤,在服役第60年遭遇该地震时的损伤值最大,超过设计值17%,且在服役第55年和第60年遭遇地震时的损伤均超出了相应设防损伤限值,可认为结构处于“倒塌”状态.与图4(b)比较发现,前者引起的损伤远大于后者,且波动性也较后者显著.服役第50~60年期间遭遇罕遇地震时的时变损伤明显高于前期,说明刚度变化所引起的抗侧向作用能力的变化可能是影响结构时变损伤值的主要因素.

(a) 罕遇地震
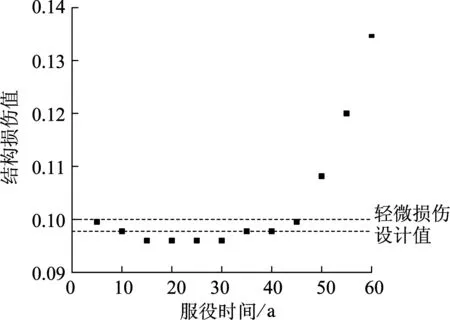
(b) 多遇地震
为更好地理解地震作用的增强对结构振动形态的影响,图5给出了罕遇和多遇地震下部分服役期的层间位移变化情况.可发现,罕遇地震下结构振动形态较为紊乱,究其原因,可能是由于地震作用越强,刚度变化带来的结构传导能力的下降也越发显著,从而导致结构振动形态显著改变,也加剧了时变损伤值的波动性.
进一步对T2-Ⅱ-2波和Northridge波下的结构损伤时变特性加以分析.图6(a)和(b)分别为罕遇和多遇地震(T2-Ⅱ-2波)下基于整体法的损伤值.由图6(a)看出,损伤呈现显著的波动性,存在部分服役期内损伤小于设计值的现象,在服役55年遭遇地震时结构时变损伤达到最大.在整个服役期间和设计条件下,损伤值均超过倒塌控制限值0.8,结构可能倒塌.与图4(a)对比发现,在遭遇罕遇地震T2-Ⅱ-2波时的时变损伤值要大于E1-Centro波时的损伤,且前者的波动性也强于后者,说明结构在遭遇不同波形的地震时,时变损伤有一定差别,地震波对于结构的作用越强时,时变损伤值越大,波动性也越大.对比图6(a)与(b)的振动形态可发现,不同地震强度下同一波形的结构时变损伤值和波动性差异较大,究其原因,可能是由于地震作用增强时,大量构件进入塑性,地震传导能力变化显著,从而引起了波动性的差异.
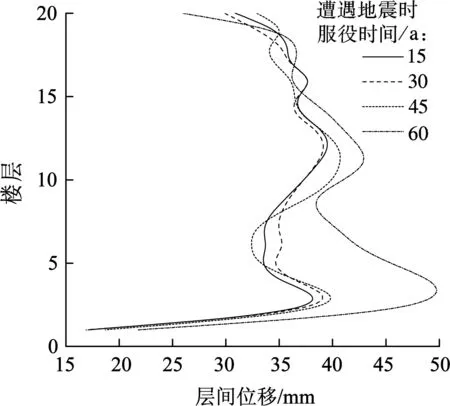
(a) 罕遇地震
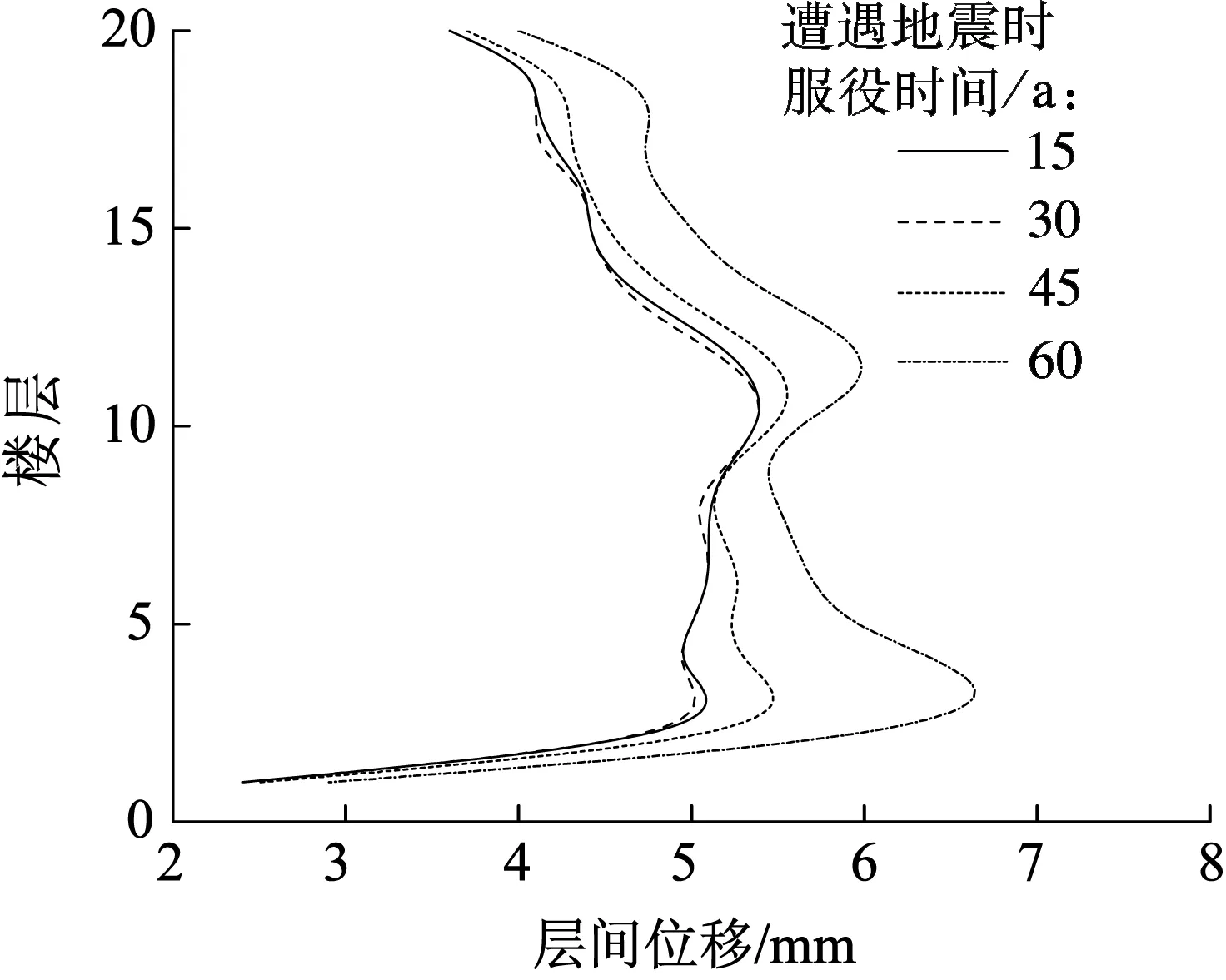
(b) 多遇地震
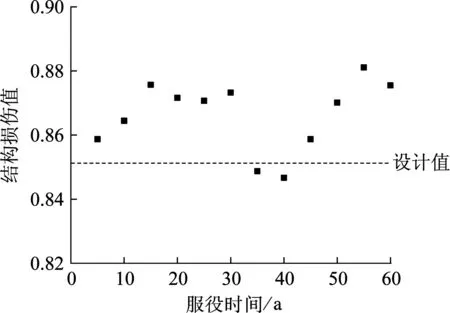
(a) 罕遇地震
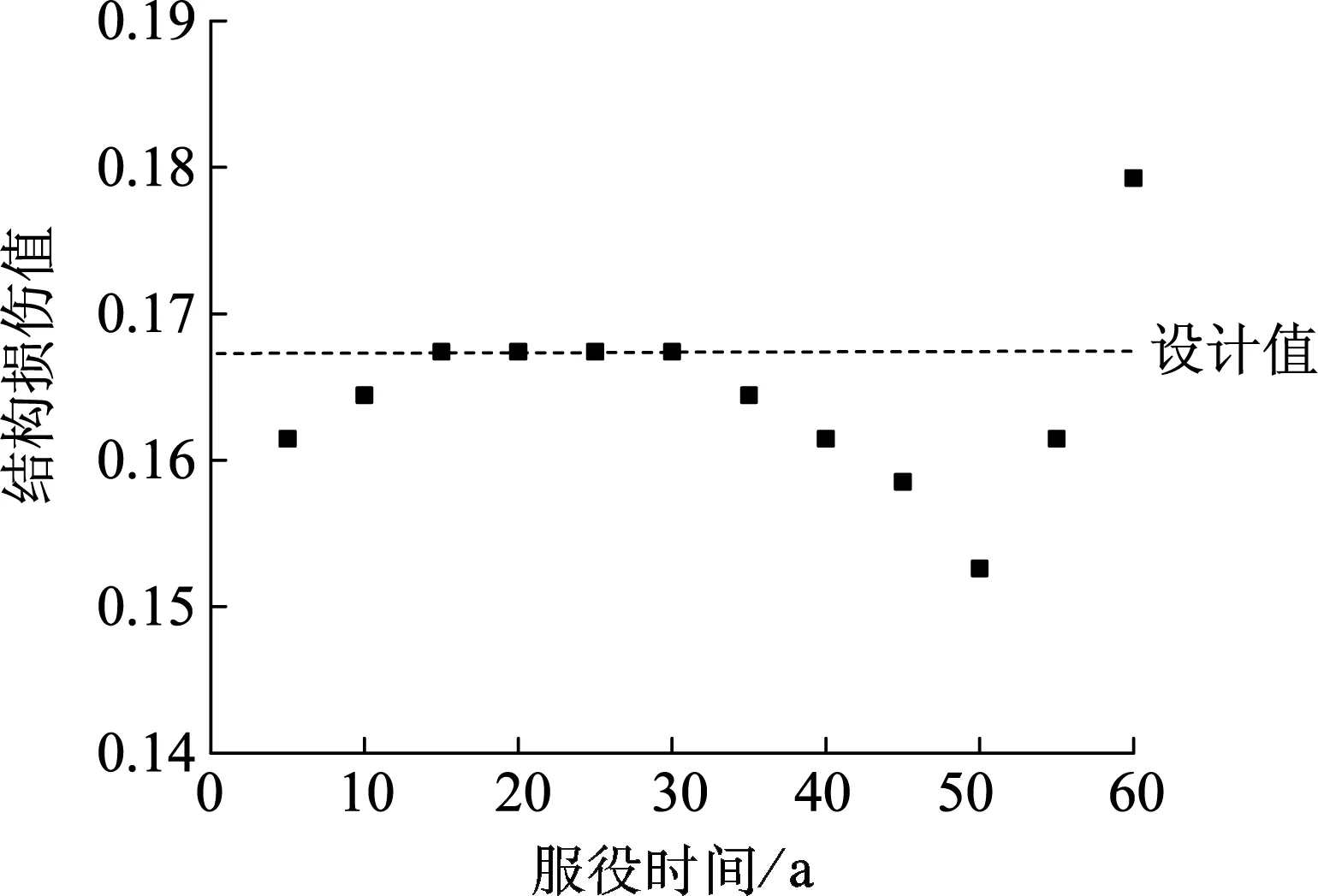
(b) 多遇地震
此外,结构在遭遇罕遇地震T2-Ⅱ-2波时的振动形态相比E1-Centro波时更加紊乱,如图7所示.服役第45年遭遇地震时的振动形态与其他年份相比有显著不同.观察服役第45年遭遇地震时的振动形态可发现,下部楼层的层间位移增大,而上部楼层的层间位移减小,导致最大层间位移减小,这正是导致该年遭遇地震时的损伤值小于其他服役年限的原因.同时也说明了结构底部楼层进入塑性消耗了大量地震作用,使传导至上部结构的地震作用减小,由此可以较好地解释地震传导能力和抗侧向力作用的双重影响会改变结构的振动形态的结论.
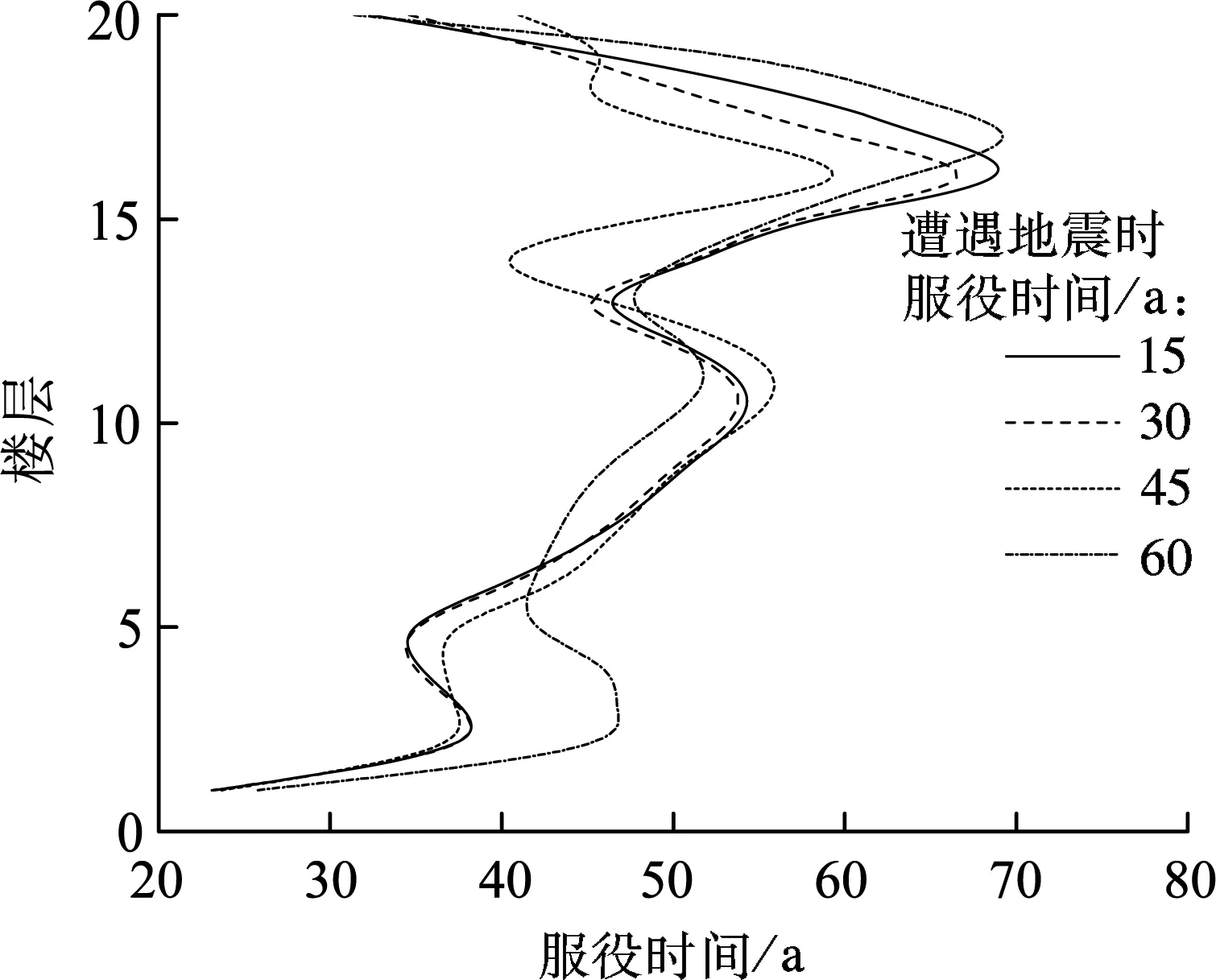
图7 遭罕遇地震(T2-Ⅱ-2波)时的层间位移
图8为服役期内遭遇罕遇地震Northridge波时的时变损伤值,可以看出损伤时变效应同样显著,服役期第25~40年、第55~60年结构遭遇地震时的损伤变化与刚度变化趋势一致,时变损伤值随刚度减小而减小;而其他年份时变损伤变化则与刚度变化超趋势相反.刚度变化带来的抗侧向作用能力下降和地震作用传导能力下降同时导致结构损伤时变的波动性.损伤值在第55年达到峰值,高出设计值6%但未达到倒塌限值,满足“大震不倒”的设防要求.结构在Northridge波作用下的时变损伤值波动性小于罕遇地震El-Centro波和罕遇地震T2-Ⅱ-2波.由图9可知,该波作用下各服役年限的层间位移变化趋势相对一致.在第15,30,45年遭遇地震时,结构振动形态变化不显著.服役期60年遭遇地震时,结构刚度下降,下部楼层层间位移增大,传导至上部结构的地震作用减小.

图8 罕遇地震(Northridge波)下的时变损伤
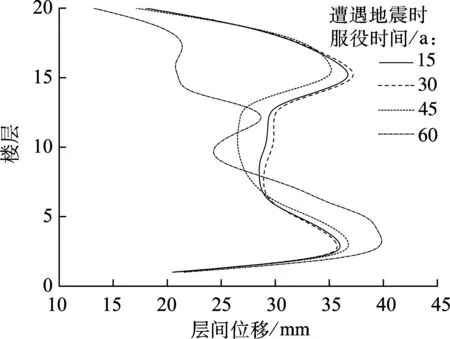
图9 遭罕遇地震(Northridge波)时的层间位移
对比结构在不同服役期下遭遇罕遇地震时的层间位移变化可以看出,地震作用越强,其振动形态变化越显著,损伤受刚度下降的影响也越显著,导致结构在服役期内遭遇地震时的时变损伤值变化波动性加剧,振动形态也更加紊乱.
5.3 基于加权组合法的结构损伤特性研究
整体法虽在一定程度上反映了结构在罕遇地震下的损伤时变特性,但有其局限性.根据5.2节分析可知,地震作用增强时,结构振动形态会发生改变,出现最大层间位移的楼层也会相应改变.由于不同楼层的损伤对整体结构损伤程度的影响不同,因此,仅采用基于整体法的损伤模型无法准确评估结构的损伤状态.为了进一步探究服役期内结构在罕遇地震下的损伤时变机制和破坏时各类构件的损伤情况,本节采用加权组合模型研究结构的损伤时变特性.
结构在罕遇地震E1-Centro波下,采用加权组合模型获得的时变损伤如图10所示.可以看出,损伤依然呈现时变特性,均不同程度上大于设计值.在服役20年时损伤最小,在服役40年以后基本呈增长趋势,服役60年时损伤最大,但总体上变化幅度不大.
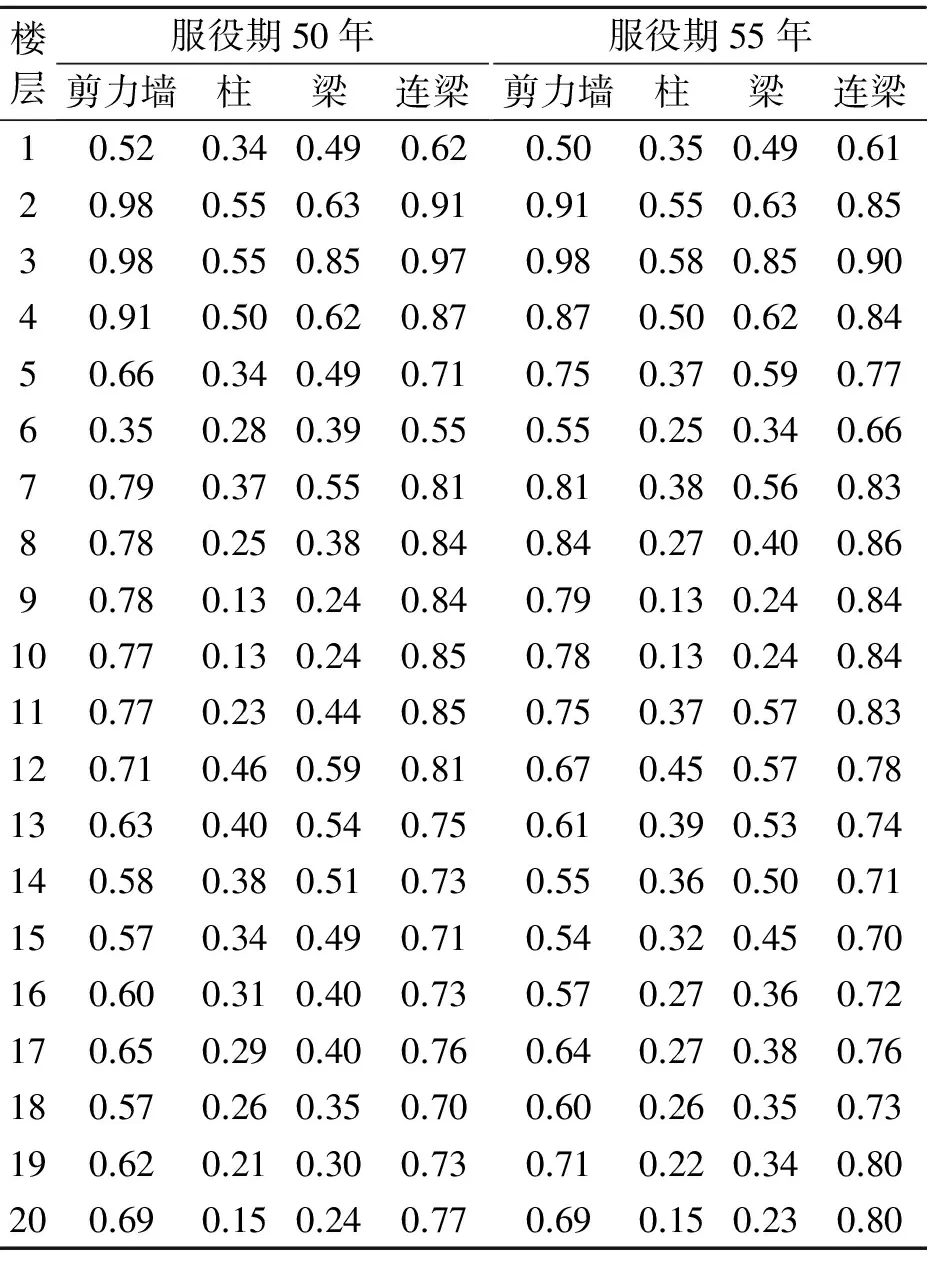
将图10采用加权组合法得到的损伤值与图4(a)的基于整体法的损伤模型的结果相比,可以发现前者在损伤过程中不仅考虑了竖向承载构件的损伤,而且考虑了型钢梁、混凝土连梁等构件的损伤,故采用加权组合法所获得的时变损伤与整体法并不相同,各楼层中各类构件的损伤均值如表8所示.服役50和55年遭遇地震时结构刚度、楼层和构件的损伤均有一定程度的改变.最终,基于整体法得到的损伤值继续上升,而基于加权组合法得到的损伤值有所回落.
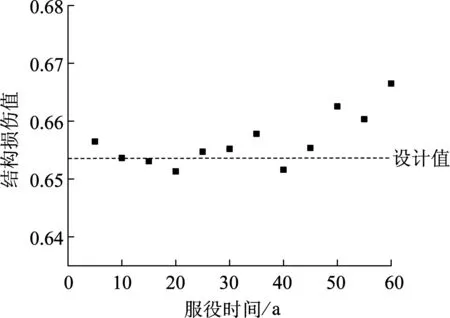
图10 罕遇地震(El-Centro波)下结构时变损伤值
表8 服役期50和55年遭遇罕遇地震(El-Centro波)时各楼层构件损伤均值
楼层服役期50年剪力墙柱梁连梁服役期55年剪力墙柱梁连梁10.520.340.490.620.500.350.490.6120.980.550.630.910.910.550.630.8530.980.550.850.970.980.580.850.9040.910.500.620.870.870.500.620.8450.660.340.490.710.750.370.590.7760.350.280.390.550.550.250.340.6670.790.370.550.810.810.380.560.8380.780.250.380.840.840.270.400.8690.780.130.240.840.790.130.240.84100.770.130.240.850.780.130.240.84110.770.230.440.850.750.370.570.83120.710.460.590.810.670.450.570.78130.630.400.540.750.610.390.530.74140.580.380.510.730.550.360.500.71150.570.340.490.710.540.320.450.70160.600.310.400.730.570.270.360.72170.650.290.400.760.640.270.380.76180.570.260.350.700.600.260.350.73190.620.210.300.730.710.220.340.80200.690.150.240.770.690.150.230.80
对比表8中不同楼层、构件的损伤,可以看出剪力墙和柱的最大损伤值出现在第3层,且在服役55年时略高.但由于其他楼层构件损伤的变化,最终导致结构在服役55年遭遇罕遇地震E1-Centro波时的时变损伤值小于服役50年遭遇该地震时的时变损伤.
运用加权组合法计算罕遇地震T2-Ⅱ-2和Northridge波下的损伤,结果如图11所示.可以看出,损伤值同样存在波动性,说明在刚度变化不显著的5~40年,地震作用传导能力的变化愈发显著,结构时变损伤虽在一定范围内波动,但整体呈现增大趋势,说明抗震能力下降对于结构损伤仍然占主导作用.
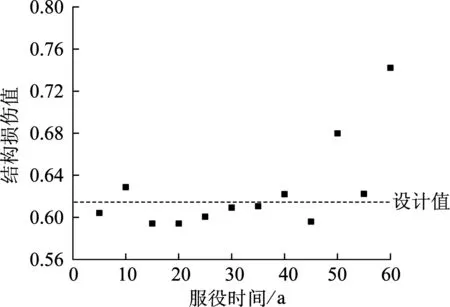
图11 罕遇地震(T2-Ⅱ-2波)下的时变损伤值(加权)
对比表9中服役60年和设计条件下的构件损伤,可以发现,在设计条件下多数构件出现不同程度损伤,连梁损伤较为严重,部分剪力墙损伤严重.在服役60年遭遇地震时,部分剪力墙、梁、连梁达到承载极限而破坏,部分型钢混凝土组合柱严重受损,多数连梁损伤大于相应楼层的剪力墙损伤.上述情况与倒塌时的状态比较接近.其中,第2~5层损伤较为严重,上部结构损伤较小.这是因为当结构刚度降低时,底部楼层承担了多数地震作用,发生严重的塑性变形和破坏,导致传递到上部结构的地震作用减小.上部结构的地震损伤减弱,验证了结构刚度降低可能导致结构的地震传导能力下降,从而使得部分构件的损伤值降低的结论.
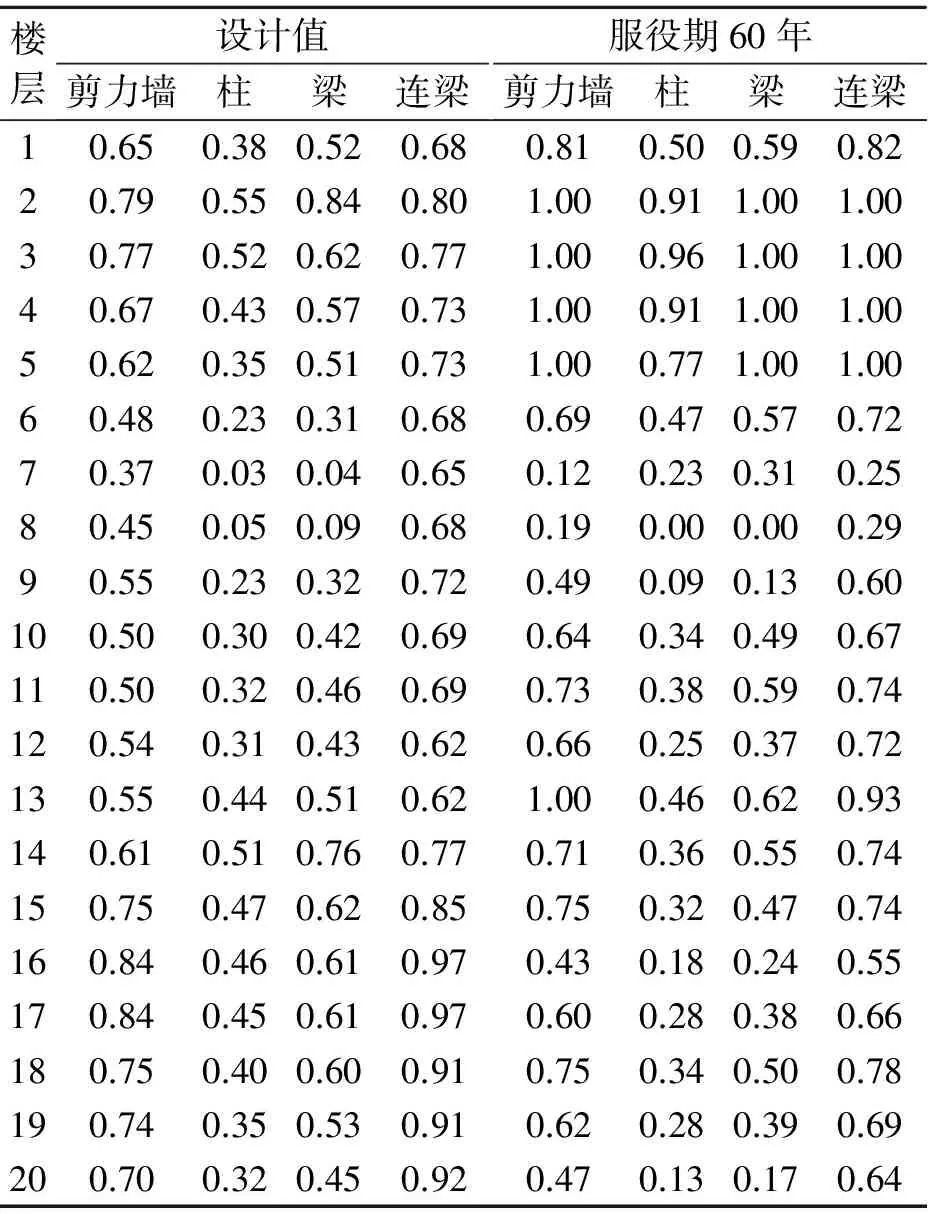
表9 设计标准下与服役期60年的各楼层构件损伤均值
最后,采用基于加权组合法分析了罕遇地震Northridge波下的时变损伤值,如图12所示.可以看出,损伤同样呈现明显的时变特性,5~45年时变损伤值较小,呈现波动性,45年后遭遇地震时的时变损伤持续增加,第60年达到最大,比设计值高出15%左右.但整个服役期内遭遇该波时的损伤基本小于E1-Centro波和T2-Ⅱ-2波.
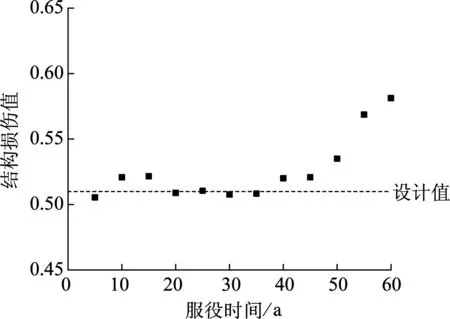
图12 罕遇地震(Northridge波)作用下时变损伤(加权)
综合对比结构遭遇上述不同地震波的损伤时变效应可以发现,在服役期后段结构刚度显著变化时损伤明显增大,个别年限发生倒塌,服役期前段损伤变化不显著.服役期大部分年限内遭遇罕遇地震时出现严重损伤,整个服役期受到结构抗侧向力变化和地震传导能力变化影响,时变损伤值呈现不同程度波动性,且在地震作用越强的地震波下,时变损伤波动越明显.
对比整体法和加权组合法所获得的罕遇地震下时变损伤均值的变化,结果如图13所示.可看出损伤呈现时变特性,特别是服役期45~60年期间,混凝土材料性能显著下降,导致结构性能改变,结构抗侧向力作用和地震传导能力均发生改变,从而引起结构的地震形态和构件损伤状态发生显著改变,结构时变损伤显著高于服役期前段.相较于整体法而言,运用加权组合法进行损伤评估时,损伤时变波动性更加显著.与不考虑材料时变的设计值对比可发现,基于整体法的最大时变损伤值超出设计值8%左右,而且超越相应的损伤限值,不符合抗震设防要求;基于加权组合法得到的最大时变损伤值超出设计值10%左右.参照基于整体法的损伤和结构性能的对应关系,可预估基于加权组合法的损伤倒塌限值应为0.65左右,若要准确评估,还应进行实验或大量数值模拟验证,以减小偶然因素的影响.
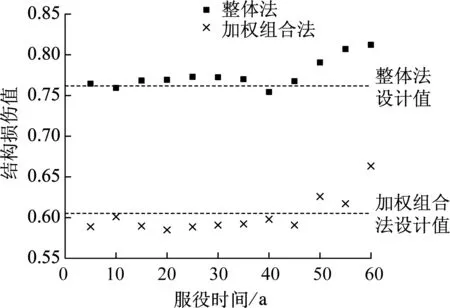
图13 罕遇地震下整体法和加权组合法的时变损伤均值
6 结论
1) 结构在服役期内遭遇罕遇地震时,基本处于严重损伤状态,损伤时变效应显著.结构振动形态变化显著,时变损伤值不断加剧,服役后期损伤整体高于前段,甚至超出倒塌限值.
2) 结构传导地震作用能力与抗侧向作用能力的共同作用可能会导致服役期内结构遭遇地震作用时的时变损伤值呈现波动性.
3) 结构刚度变化带来的结构抗侧向作用能力的变化对损伤变化起主导作用,但是地震作用越大,刚度变化带来的传导地震作用能力的影响就越大,结构时变损伤值的波动性越显著.
4) 采用整体法和加权组合法所获得的损伤时变规律基本一致,但是前者的时变损伤高于后者,可根据其相关性,建立基于加权组合法的结构性能标准.
References)
[1]赵慧玲, 叶志明. 钢-混凝土组合结构抗震性能研究进展[J]. 力学与实践, 2014, 36(1): 1-8.DOI:10.6052/1000-0879-13-104. Zhao Huiling, Ye Zhiming. Progress in seismic behavior of the composite steel-concrete structures[J].MechanicsinEngineering, 2014, 36(1): 1-8. DOI:10.6052/1000-0879-13-104.(in Chinese)
[2]杨晓巍, 李小琴, 赖靖宁, 等. 钢-混凝土组合结构界面受力行为初探[J]. 四川建筑, 36(4): 159-161, 165. DOI:10.3969/j.issn.1007-8983.2016.04.058. Yang Xiaowei, Li Xiaoqin, Lai Jingning, et al. Preliminary study of interface stress behavior of steel-concrete composite structure[J].SichuanArchitecture, 36(4): 159-161, 165. DOI:10.3969/j.issn.1007-8983.2016.04.058. (in Chinese)
[3]马辉. 型钢再生混凝土柱抗震性能及设计计算方法研究[D]. 西安: 西安建筑科技大学土木工程学院,2013
[4]杨怡亭, 侯兆新, 李国强, 等. 高强型钢混凝土组合柱小偏心受压力学性能[J]. 哈尔滨工业大学学报, 2016, 48(6): 132-137. DOI:10.11918/j.issn.0367-6234.2016.06.021. Yang Yiting, Hou Zhaoxin, Li Guoqiang, et al. Mechanical properties of high strength steel reinforced concrete columns under small eccentric load[J].JournalofHarbinInstituteofTechnology, 2016,48(6): 132-137. DOI:10.11918/j.issn.0367-6234.2016.06.021. (in Chinese)
[5]李晓蕾, 卢俊龙, 张超. RC短肢剪力墙地震损伤特征与模型研究[J]. 地震工程与工程振动, 2016,36(3): 68-75. DOI:10.13197/j.eeev.2016.03.67.lixl.009. Li Xiaolei, Lu Junlong, Zhang Chao. Damage characteristics and seismic damage model of RC short-pier shear wall[J].EarthquakeEngineeringandEngineeringDynamics, 2016, 36(3): 68-75. DOI:10.13197/j.eeev.2016.03.67.lixl.009.(in Chinese)
[6]侯丕吉. 型钢高强高性能混凝土框架柱地震损伤模型研究[D]. 西安:西安建筑科技大学土木工程学院, 2009.
[7]Park Y J, Ang A H S, Wen Y K. Seismic damage analysis of reinforced concrete buildings[J].JournalofStructuralEngineering,ASCE, 1985, 111(4): 740-757. DOI:10.1061/(asce)0733-9445(1985)111:4(740).
[8]欧进萍, 牛荻涛. 地震地面运动随机过程模型的参数及其结构效应[J]. 哈尔滨建筑工程学院学报, 1990, 23(2): 24-34. Ou Jinping, Niu Ditao. Parameters in the random process models of earthquake ground motion and their effects on the response of structures[J].JournalofHarbinUniversityofCivilEngineeringandArchitecture, 1990, 23(2): 24-34. (in Chinese)
[9]杜修力, 欧进萍. 建筑结构地震破坏评估模型[J]. 世界地震工程, 1991,7(3): 52-58. Du Xiuli, Ou Jinping. Earthquake damage assessment model of construction structure [J].WorldEarthquakeEngineering, 1991, 7(3): 52-58. (in Chinese)
[10]蒋欢军, 朱剑眉, 陈前. 超高层钢-混凝土混合结构地震损伤模型研究[J]. 振动与冲击,2014, 33(4): 77-83. DOI:10.3969/j.issn.1000-3835.2014.04.015. Jiang Huanjun, Zhu Jianmei, Chen Qian. Seismic damage model for steel-concrete composite structure of ultra-tall buildings [J].JournalofVibrationandShock, 2014, 33(4): 77-83. DOI:10.3969/j.issn.1000-3835.2014.04.015. (in Chinese)
[11]钟文, 潘坚文. 堆石混凝土抗压强度影响因素细观分析[J]. 水力发电学报, 2016, 35(5): 15-22. DOI:10.11660/slfdxb.20160502. Zhong Wen, Pan Jianwen. Meso-scale analysis of influence factors on compressive strength of rock-filled concrete using particle-based discrete element method[J].JournalofHydroelectricEngineering, 2016, 35(5): 15-22. DOI:10.11660/slfdxb.20160502.(in Chinese)
[12]高向玲, 颜迎迎, 李杰. 一般大气环境下混凝土经时抗压强度的变化规律[J]. 土木工程学报, 2015, 48(1): 19-26. Gao Xiangling, Yan Yingying, Li Jie. Change law of time-dependent concrete compressive strength in the atmospheric environment [J].ChinaCivilEngineeringJournal, 2015, 48(1): 19-26. (in Chinese)
[13]朱彦鹏. 混凝土结构设计原理[M]. 重庆:重庆大学出版社, 2002: 11-22.
[14]黄志华, 吕西林, 周颖, 等. 高层混合结构地震整体损伤指标研究[J]. 同济大学学报(自然科学版), 2010, 38(2): 170-177. DOI:10.3969/j.issn.0253-374x.2010.02.004. Huang Zhihua, Lü Xilin, Zhou Ying, et al. Studies on global seismic damage indices of high-rise hybrid structures[J].JournalofTongjiUniversity(NaturalScience), 2010, 38(2): 170-177. DOI:10.3969/j.issn.0253-374x.2010.02.004.(in Chinese)
[15]Banon H, Irvine H M, Biggs J M. Seismic damage in reinforced concrete frames[J].JournaloftheStructuralDivision, 1981, 107(9): 1713-1729.
[16]Scott B D, Park R, Priestley M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J].ACIJournal,1982, 79(2): 13-27.
[17]Gomes A, Appleton J. Nonlinear cyclic stress-strain relationship of reinforcing bars including buckling[J].EngineeringStructures, 1997, 19(10): 822-826. DOI:10.1016/s0141-0296(97)00166-1.
Time-dependent damage characteristics of steel-concrete composite structures under rarely occurred earthquake
Wang Ying1Wang Ruozhu2Li Zhaoxia1
(1Jiangsu Key Laboratory of Engineering Mechanics, Southeast University, Nanjing 210096, China) (2Changzhou District Government Offices Administration,Changzhou 213001, China)
For steel-concrete composite structure, the dynamic elastic-plastic time history analysis method is utilized to obtain the structural dynamic response under the rarely occurred earthquake. The seismic damage time-dependent model, which integrates global method and weighting combination method, respectively, is utilized to study the structural damage time-dependent characteristics under the rarely occurred earthquake. Considering that the parameters such as the stiffness and the damping are constants in the calculation but have the variable characteristics in the whole service period, they are treated as pseudo variables. A typical steel-concrete composite sample is studied. The results show that the damage has significantly time-dependent characteristics under rare earthquake and maybe exceeds the performance limits specified in the code. The stiffness change can cause the changes of lateral resistance force and earthquake conduction ability, thus leading to the significant fluctuations of the time-dependent damage. The influence of lateral resistance force on damage plays a dominant role. The more severe the earthquake, the greater the effect of earthquake conduction ability on damage. This can lead to more significant fluctuation of damage and vibration shapes. Comparing the time-dependent damage values and the design values without considering material time-dependent characteristics, it can be found that the material time-dependent characteristics have an important effect on the accuracy of the seismic design and evaluation.
steel-concrete composite structure; time-dependent damage; time-dependent characteristics; dynamic elastic-plastic time-history analysis
10.3969/j.issn.1001-0505.2017.04.022
2016-11-15. 作者简介: 王莹(1980—),女,博士,副教授; 李兆霞(联系人),女,博士,教授,博士生导师,zhxli@seu.edu.cn.
国家自然科学基金资助项目(51678135,51008069,11072060)、中央高校基本科研业务费专项资金资助项目.
王莹,王若竹,李兆霞.罕遇地震下钢混组合结构损伤时变特性[J].东南大学学报(自然科学版),2017,47(4):766-775.
10.3969/j.issn.1001-0505.2017.04.022.
O346.1
A
1001-0505(2017)04-0766-10

