再生混凝土力学性能的应变率敏感性数值模拟

李 龙 肖建庄 黄凯文

(1同济大学土木工程学院, 上海 200092)(2香港理工大学建设与环境学院, 香港999000)

再生混凝土力学性能的应变率敏感性数值模拟

李 龙1, 2肖建庄1黄凯文1

(1同济大学土木工程学院, 上海 200092)(2香港理工大学建设与环境学院, 香港999000)

基于九骨料模型再生混凝土建立了有限元模型,研究了再生混凝土力学性能的应变率敏感性以及细观相材料应变率敏感性对其的影响,并讨论了再生粗骨料取代率和新、老砂浆强度对再生混凝土应变率敏感性的影响．结果表明,该有限元模型能较好地模拟再生混凝土力学性能的应变率敏感性;再生混凝土峰值应力和弹性模量随着应变率的增大近乎线性增大,且弹性模量呈现更加均匀的增长趋势;相比骨料和界面过渡区,砂浆的应变率敏感性对再生混凝土整体应变率敏感性起主导作用;再生粗骨料取代率增大或新、老砂浆强度降低时,再生混凝土的弹性模量应变率敏感性增大,但它们对再生混凝土峰值应力应变率敏感性的影响有所不同．

再生混凝土;力学性能;应变率敏感性;数值模拟;再生粗骨料取代率

再生混凝土技术被认为是解决废混凝土问题的最有效措施之一．近年来，国内外大量学者对其进行了研究．许多研究表明,再生混凝土的强度和弹性模量等力学性能指标要低于相同水灰比的普通混凝土[1-3]．Xiao等[4]总结了过去15年国内学者对再生混凝土的研究工作,包括再生混凝土的细微观性能、力学性能、耐久性能以及结构性能．然而,目前学者对再生混凝土力学性能的研究基本还局限于静态力学性能的范围,其动态力学性能方面的研究较少．而工程结构在其生命周期内均有可能遭受地震、冲击等动荷载的作用,因此研究再生混凝土的动态力学性能对其在工程结构中的应用非常重要．

混凝土是一种应变率敏感性(简称率敏感性)材料,其强度和变形等性质均随应变率的变化而变化．1917年,Abrams[5]发现混凝土的抗压强度存在率敏感性，之后人们对混凝土不同应变率下的动态力学性能进行了广泛的研究．1991年,Bischoff等[6]对过去大量研究者对混凝土动态受压性能的工作进行了综述．1998年,Malvar等[7]总结了应变率对混凝土受拉性能影响的研究成果．然而,目前仅有少量再生混凝土动态力学性能相关的研究工作．例如,Lu等[8]对再生混凝土的冲击性能进行了初步研究;Rao等[9]对不同再生骨料取代率下的再生混凝土梁的冲击性能进行了研究;Xiao等[10-11]对再生混凝土在中低应变率以及高应变率下的动态力学性能进行了试验研究;肖建庄等[12]基于九骨料模型再生混凝土试件对再生混凝土的动态力学性能进行了试验研究．因此,有必要对再生混凝土动态力学性能进行更深入的研究．

本文在文献[12]试验研究的基础上,基于九骨料模型再生混凝土建立了有限元模型,对再生混凝土力学性能的率敏感性进行了数值模拟以及变参数分析．

1 有限元模型

1.1 几何模型

该模拟中再生混凝土试件采用平面几何模型,其与文献[12]中的九骨料模型再生混凝土试件的平面尺寸相同．该模型由五相材料构成,即天然骨料、老砂浆、新砂浆、老界面过渡区以及新界面过渡区,如图1所示．

过去大量研究表明,界面过渡区尺寸非常小．随着纳米压痕技术的出现,目前已可以直接测量界面过渡区的微观力学特征．Xiao等[13]研究表明,老界面过渡区和新界面过渡区的厚度分别约为50和60 μm．因此,本模拟中老界面过渡区和新界面过渡区的厚度分别设置为50和60 μm,沿径向仅划分为2个单元，并且均采用4节点平面应力缩减积分单元(CPS4R)．采取扫掠方式划分网格,划分好的网格如图2所示．

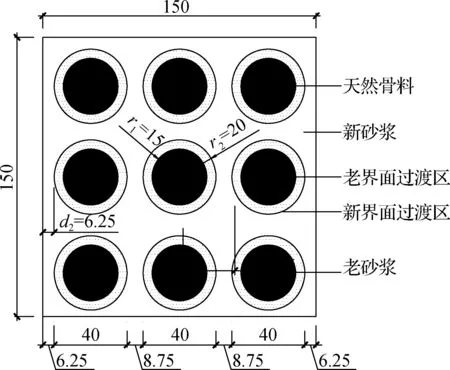
图1 再生混凝土模型(单位:mm)

(a) 整体 (b) 局部

1.2 材料参数

1.2.1 天然骨料材料参数

文献[12]研究表明,在各应变率下均未出现天然粗骨料开裂或者破坏的现象．因此,本文假定天然骨料在加载过程中始终处于弹性阶段,在该模拟中定义其为各向同性线弹性材料．花岗岩也是率敏感性材料,但相比砂浆和混凝土其率敏感性较低[14]．因此本文考虑骨料具有率敏感性,通过提高天然骨料的弹性模量来考虑其率敏感性,应变率每提高一级,设定天然骨料的弹性模量增加2.5%．本模拟中天然骨料的准静态弹性模量取70 GPa[15],泊松比均取0.16．

1.2.2 砂浆和界面过渡区材料参数

在本模拟中,砂浆和界面过渡区的本构关系均采用ABAQUS中的混凝土损伤塑性模型．采用该模型进行计算时,需要用户输入材料的受拉应力-开裂应变关系、受压应力-非弹性应变关系、材料受拉损伤因子-开裂应变关系和受压损伤因子-非弹性应变关系．本文结合《混凝土结构设计规范》(GB 50010—2010)给出的应力-应变关系来确定具体参数．

对于单轴受拉应力-应变关系,假定在达到破坏应力之前为线弹性,取峰值点的割线模量作为初始弹性模量Et．而非弹性阶段的应力-应变关系采用规范推荐的公式．因此单轴受拉应力-应变关系按下式确定:

(1)

(2)

式中,σt为受拉应力;εt为受拉应变;αt为单轴受拉应力-应变关系曲线下降段参数值;ft为单轴抗拉强度代表值;εtp为受拉峰值应变．

对于单轴受压应力-应变关系,假定应力小于峰值应力的1/2时应力-应变曲线为线弹性,混凝土的初始切线弹性模量为Ec．强化段和软化段应力-应变关系采用规范推荐的公式．因此,单轴受压应力-应变关系按下式确定:

(3)

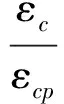
(4)

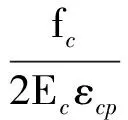
(5)

式中,σc为受压应力;εc为受压应变;αc为单轴受压应力-应变关系曲线下降段参数值;fc为单轴抗压强度代表值;εcp为受压峰值应变．

在ABAQUS软件中的混凝土损伤塑性模型中,受拉损伤因子-开裂应变关系和受压损伤因子-非弹性应变关系可分别按下式确定:

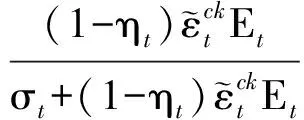
(6)

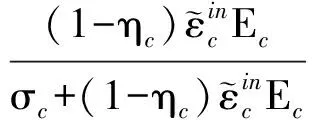
(7)

本模拟中,M30砂浆在各应变率下的峰值应力是根据文献[12]中模型砂浆M30的峰值应力与应变率关系拟合曲线来确定的．本文假定随应变率的增大,M30砂浆的弹性模量与峰值应力的增幅相同．由于缺乏砂浆抗拉强度的试验数据,砂浆的抗拉强度均取为抗压强度的1/10．砂浆的受压本构曲线下降段参数αc根据规范获得,受拉本构曲线下降段参数αt均取2．在各应变率下,砂浆的其他材料参数(如εcp,ηc,εtp和ηt)均采用相同的数值．本模拟中,M30砂浆在各应变率下的各材料参数的取值如表1所示,在各应变率下的单轴受拉和单轴受压应力-应变曲线如图3所示．

表1 M30砂浆本构参数

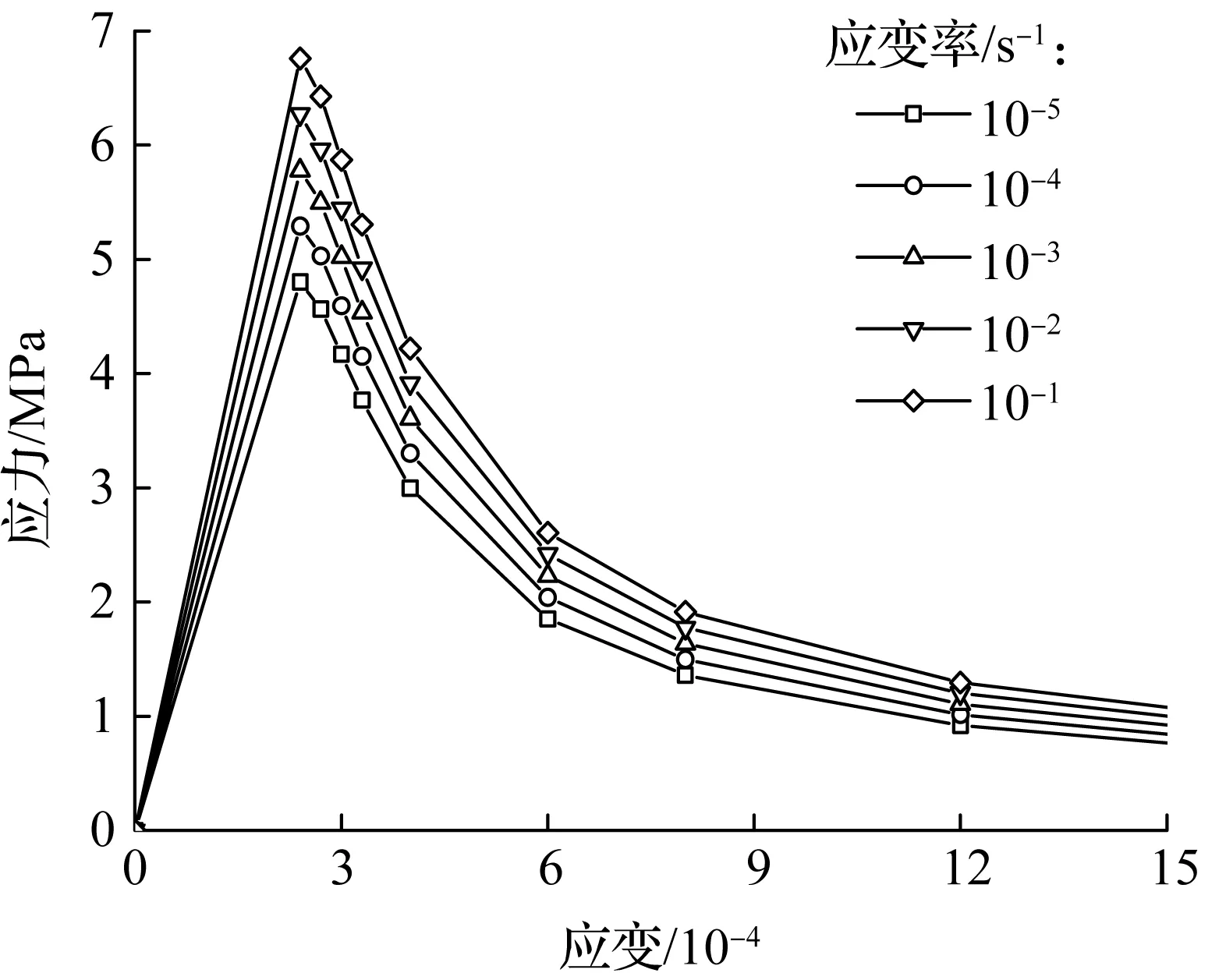
(a) 受拉

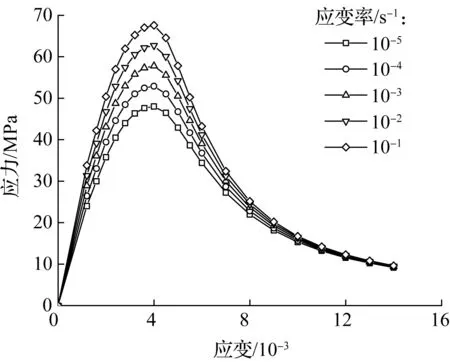
(b) 受压

图3 M30砂浆单轴受拉和受压应力-应变曲线

Xiao等[13]研究表明界面过渡区的弹性模量和强度约为对应砂浆的80%～85%,并且可采用与砂浆相似的本构模型．因此,界面过渡区的本构模型也采用混凝土损伤塑性模型,界面过渡区的抗压强度、抗拉强度和弹性模量均取为对应砂浆的0.8倍．其他参数的取值方法与砂浆一致．

1.3 加载与求解

本模拟采用ABAQUS/Explicit显式求解器求解．在试件顶部定义均匀分布位移荷载,通过位移控制模式加载．为得到完整的应力-应变曲线,本文设定Y向位移为0.9 mm时结束加载,对应的应变为6.0×10-3．底部所有节点Y向自由度限制,X向自由度和转动自由度不作限制．对底面各单元节点反力求和即为整个试件受力,除以受力面积即可得到试件的应力;顶面各节点位移即为整个试件的位移,除以试件高度即可得到试件的应变,如此可得到整个试件的应力-应变曲线．

2 有限元模型校核

在本模拟中,MRAC30-30代表新老砂浆均采用M30的再生混凝土,用于与试验中MRAC30试件进行对比．将本模拟得到的MRAC30-30在各应变率下的应力-应变曲线与试验中同应变率且峰值应力相近的应力-应变曲线进行对比,如图4所示．结果表明,在各应变率下,本模拟得到的应力-应变曲线的上升段与试验结果吻合较好,而不同之处在于模拟得到的应力-应变曲线下降段的下降趋势比试验结果更陡,其可能原因如下:该模拟中新老砂浆、新老界面过渡区的应力-应变曲线的下降段参数均取为相同强度混凝土的下降段参数,但由于骨料取为线弹性材料,超过峰值荷载后荷载下降时,骨料会回弹,使整体变形相对较小,从而使得模型试件(即新老砂浆、新老界面过渡区与骨料构成的整体)在下降段的下降趋势比实际的混凝土材料更陡．因此,在采用该有限元模型进行模拟时,新老砂浆、新老界面应力-应变曲线的下降段参数值应高于相同强度混凝土的下降段参数值,然而其取值方法还有待进一步研究．

虽然应力-应变曲线的下降段与试验结果有所差异,但它并不影响对再生混凝土力学性能率敏感性的分析,因为主要力学性能指标均可以通过应力-应变曲线上升段获得．下面将通过对比试验和模拟结果中峰值应力、弹性模量以及峰值应变随应变率变化的情况,来说明采用该有限元模型研究再生混凝土力学性能率敏感性的可靠性．

(a) 应变率为10-5/s

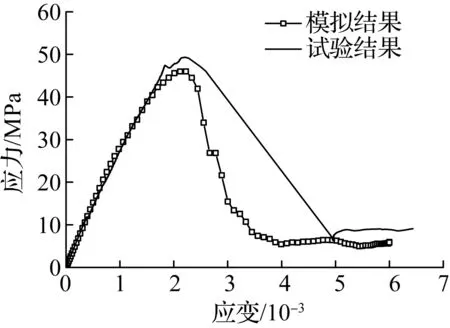
(b) 应变率为10-4/s

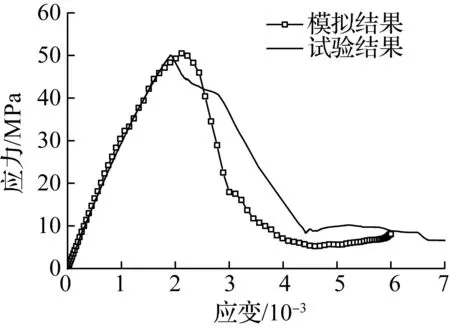
(c) 应变率为10-3/s

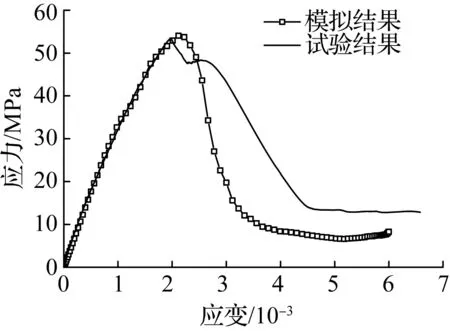
(d) 应变率为10-2/s

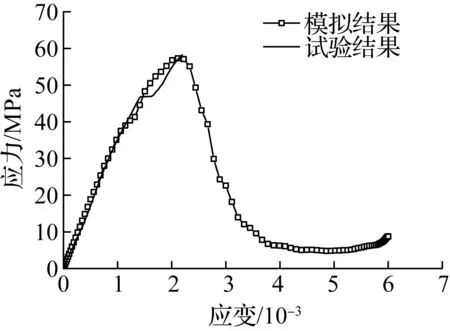
(e) 应变率为10-1/s

图5比较了试验和模拟结果中各力学指标与应变率的关系．由图可见,模拟结果中峰值应力、弹性模量及峰值应变与试验结果的均值差别不大,并且模拟和试验结果中峰值应力、弹性模量以及峰值应变随应变率的增大呈现较为一致的变化规律,即峰值应力和弹性模量随应变率的增大而增大,峰值应变随应变率的增大总体上呈现上下波动的趋势．而模拟和试验结果的差异主要来自试验结果的离散性．在模拟结果中,细观相材料都是均匀、确定的,消除了离散性,从而使得峰值应力和弹性模量随应变率的增大而增加更为均匀,峰值应变的波动幅度也较小．因此,可以认为该有限元模型能较好地模拟再生混凝土力学性能的率敏感性．

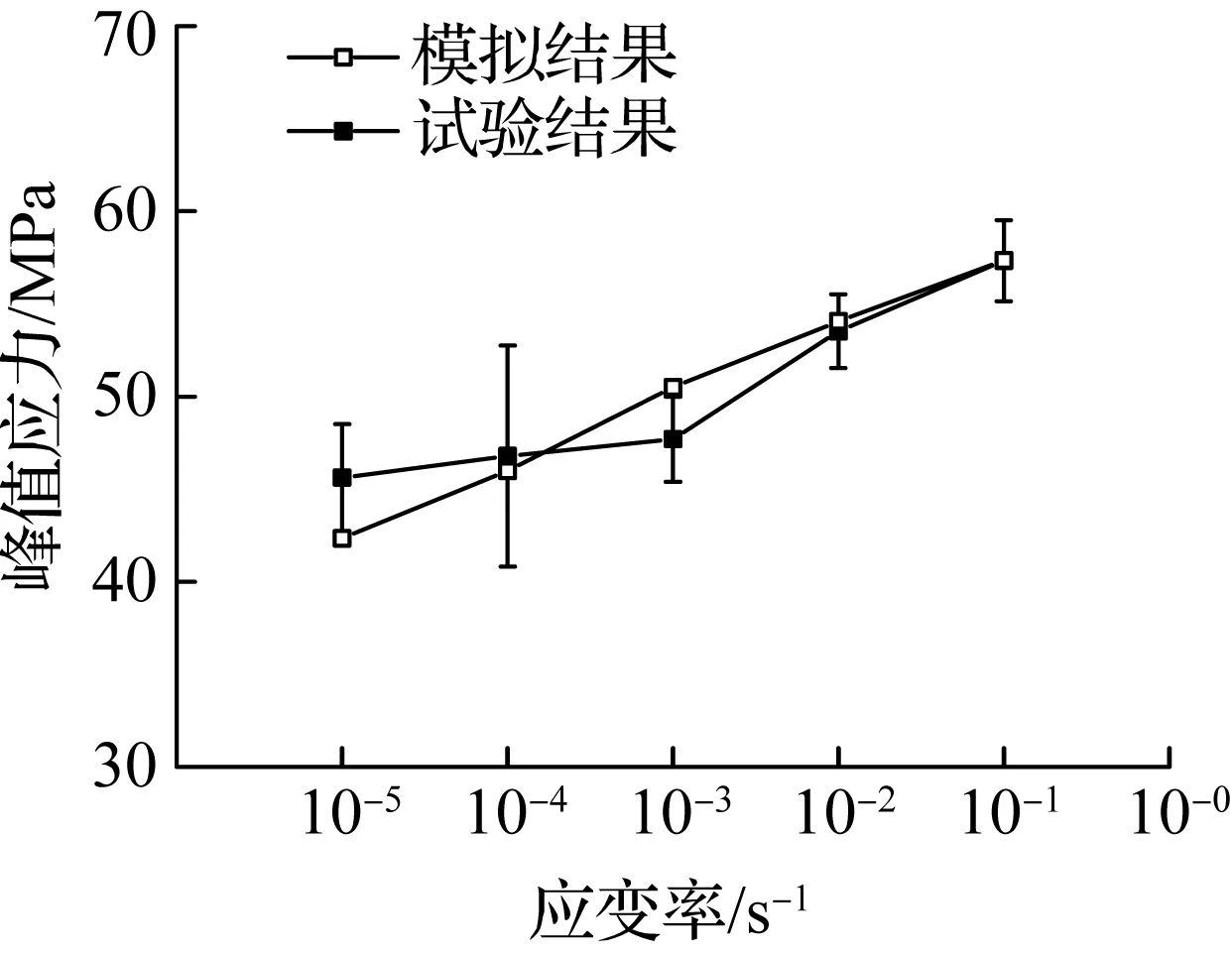
(a) 峰值应力与应变率关系

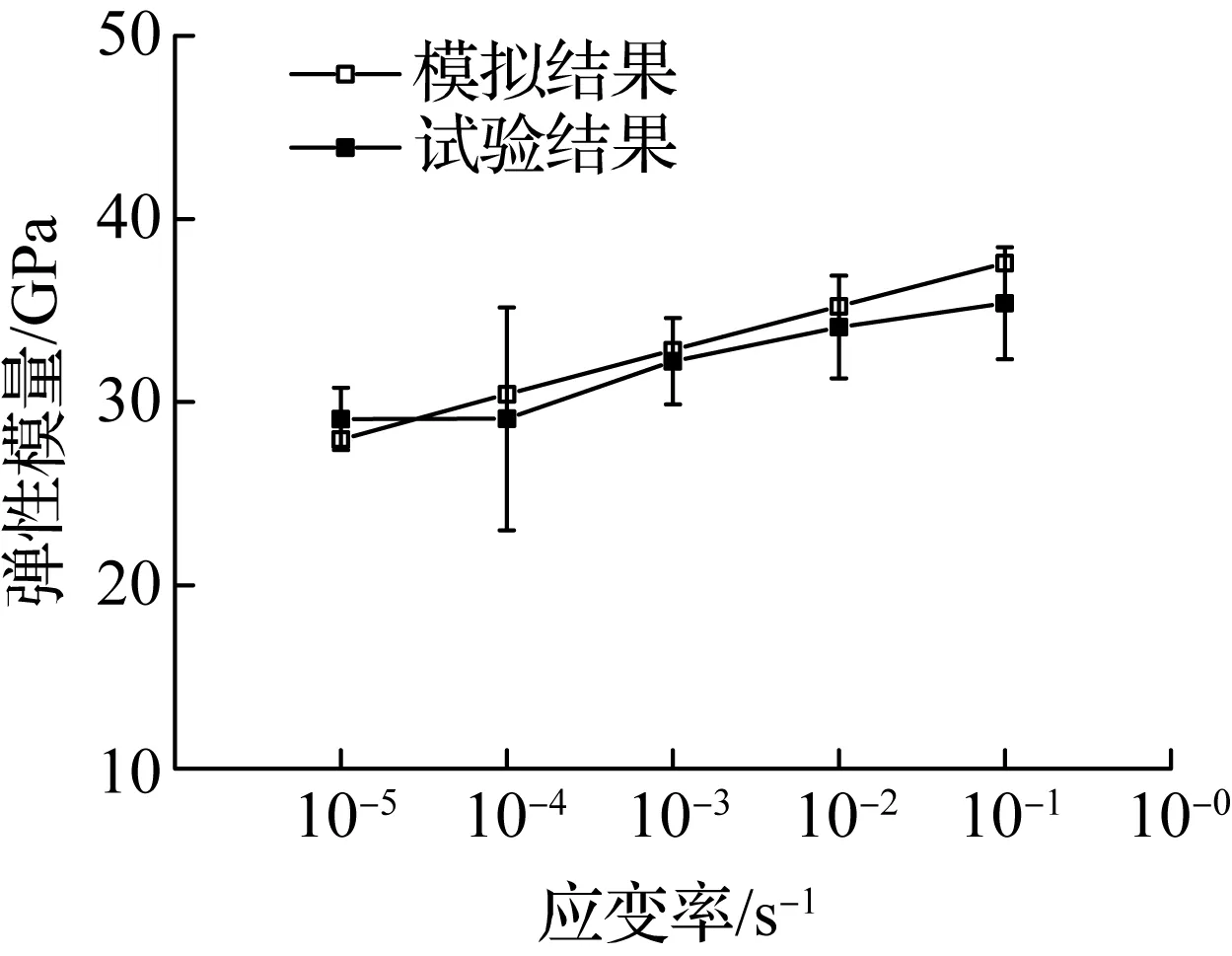
(b) 弹性模量与应变率关系

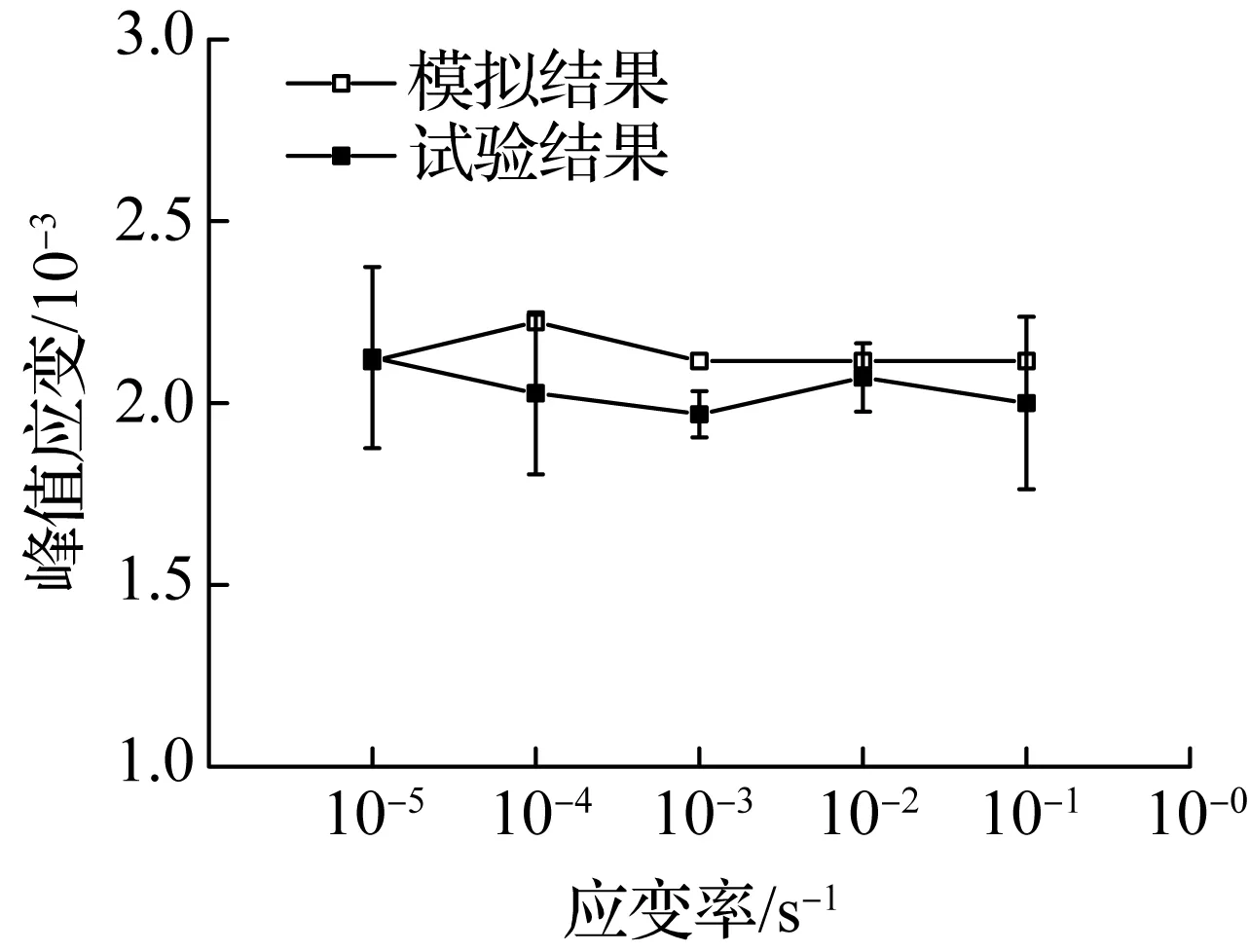
(c) 峰值应变与应变率关系

3 细观相材料率敏感性的影响

本文中材料的率敏感性是通过峰值应力动态增长因子(Df)和弹性模量动态增长因子(DE)随应变率的增大而变化的趋势来表征的．Df和DE分别代表动荷载下的峰值应力和弹性模量与准静态荷载下的峰值应力和弹性模量的比值．模拟结果表明,MRAC30-30的率敏感性高于骨料的率敏感性,低于砂浆和界面过渡区的率敏感性．事实上,MRAC30-30的率敏感性可视作是细观各相材料的率敏感性的加权平均值,各相材料所占的权重有所不同．为了探讨细观相材料对再生混凝土整体率敏感性的影响,下面将通过分别仅考虑骨料、砂浆和界面过渡区的率敏感性来研究其对再生混凝土整体率敏感性的影响．

3.1 对峰值应力率敏感性的影响

分别仅考虑骨料、砂浆和界面过渡区的率敏感性时,再生混凝土的Df与应变率的关系如图6所示．结果表明,当仅考虑骨料的率敏感性时,再生混凝土的Df随应变率的增大几乎没有改变,说明骨料的率敏感性对整体峰值应力的率敏感性几乎没有影响,这是因为在各应变率下骨料均处于弹性阶段,对整体峰值应力的影响很小;当仅考虑界面过渡区的率敏感性时,再生混凝土的Df随应变率的增大有一定程度增大,说明其对整体峰值应力率敏感性有一定影响;当仅考虑砂浆的率敏感性时,再生混凝土的Df随应变率的增大显著增大,而且其增长速度接近考虑所有细观相材料率敏感性时的情况．总体而言,相对于骨料和界面过渡区,砂浆部分的率敏感性对再生混凝土整体的峰值应力率敏感性的影响起主导作用．

图6 考虑细观相材料率敏感性时Df与应变率的关系

3.2 对弹性模量率敏感性的影响

分别仅考虑骨料、砂浆和界面过渡区的率敏感性时再生混凝土的DE与应变率的关系如图7所示．结果表明,当仅考虑骨料的率敏感性时,再生混凝土的DE随应变率的增大略有增长,说明骨料的率敏感性对整体弹性模量率敏感性有影响,但影响较小;当仅考虑界面过渡区的率敏感性时,再生混凝土的DE随应变率的增大仅有微小增长,其增长速度甚至小于只考虑骨料率敏感性的情况,说明界面过渡区的率敏感性对整体弹性模量率敏感性的影响很小,且远小于其对整体峰值应力率敏感性的影响程度;当仅考虑砂浆的率敏感性时,再生混凝土的DE随应变率的增大有显著增长,其增长速度接近考虑所有相材料率敏感性的情况,说明再生混凝土试件整体的弹性模量率敏感性主要受砂浆的率敏感性影响．

图7 考虑细观相材料率敏感性时DE与应变率的关系

4 变参数设计及结果分析

为了研究再生粗骨料取代率(简称取代率)对再生混凝土率敏感性的影响,该模拟中考虑了5个取代率,即0,33%,55%,66%,100%．在本模拟中,所有材料参数均不发生改变,仅将MRAC30-30中的部分老砂浆和老界面过渡区的材料参数赋予骨料的材料参数,这就相当于将再生粗骨料替换成天然粗骨料．

为了研究新、老砂浆强度对再生混凝土率敏感性的影响,本模拟设置了不同新砂浆的3种试件,即MRAC30-20,MRAC30-30和MRAC30-40,分别代表老砂浆为M30,新砂浆为M20,M30和M40的再生混凝土试件．设置了不同老砂浆的3种试件,即MRAC20-30,MRAC30-30和MRAC40-30,分别代表新砂浆为M30,老砂浆为M20,M30和M40的再生混凝土试件．M20,M30和M40的强度和弹性模量的比值均为0.75∶1∶1.25．考虑到混凝土类材料的强度越低,其率敏感性越显著的特征[16],本模拟设定应变率每增大一级,M20砂浆和M40砂浆的峰值应力以及弹性模量分别增加15%和5%．其他参数的变化方式与M30砂浆相同．

4.1 取代率的影响

4.1.1 取代率对峰值应力率敏感性的影响

不同取代率下再生混凝土的Df随应变率的变化如图8所示．可以发现,取代率为0时,再生混凝土的Df相对较小;取代率为33%,55%,66%和100%时,再生混凝土的Df差别不明显,例如当应变率为10-1/s时,Df分别为1.360,1.366,1.358和1.354．这说明再生混凝土的峰值应力率敏感性并非随着取代率的增大而提高或者降低,即取代率对再生混凝土峰值应力率敏感性的影响没有明确的规律．

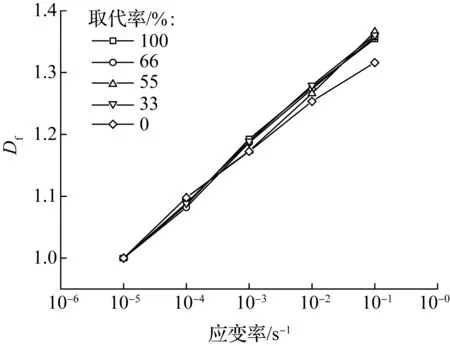
图8 不同取代率的再生混凝土的Df与应变率的关系

4.1.2 取代率对弹性模量率敏感性的影响

不同取代率下再生混凝土的DE随应变率的变化如图9所示．可发现,取代率越大,再生混凝土的DE增长越快,即再生混凝土弹性模量率敏感性越高．同时可发现,在各取代率下,随着应变率的增大,弹性模量的增长程度比峰值应力更加均匀．

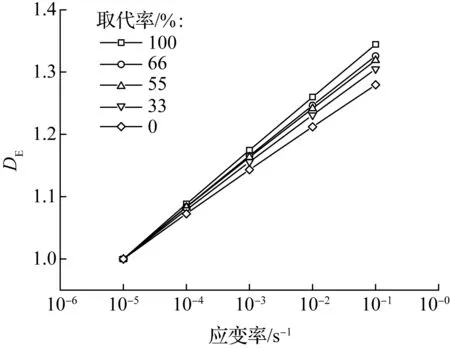
图9 不同取代率的再生混凝土的DE与应变率的关系

4.2 新砂浆强度的影响

4.2.1 新砂浆强度对峰值应力率敏感性的影响

不同新砂浆的再生混凝土的Df与应变率的关系如图10所示．可发现,新砂浆强度越高, 再生混凝土的Df增长越慢,即峰值应力率敏感性越低．

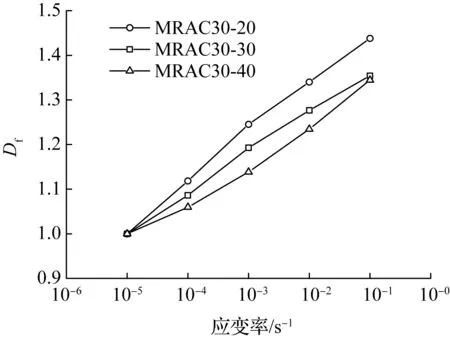
图10 不同新砂浆的再生混凝土的Df与应变率的关系

4.2.2 新砂浆强度对弹性模量率敏感性的影响

不同新砂浆的再生混凝土的DE与应变率的关系如图11所示．可发现,随着新砂浆强度的提高,再生混凝土的DE的增长速度越小,即弹性模量率敏感性越低．这与新砂浆强度对峰值应力率敏感性的影响一致．但相对峰值应力,弹性模量随着应变率的增大,其增长更加均匀．新砂浆强度改变时,再生混凝土的DE的增长速度的改变比Df的增长速度的改变更加均匀．

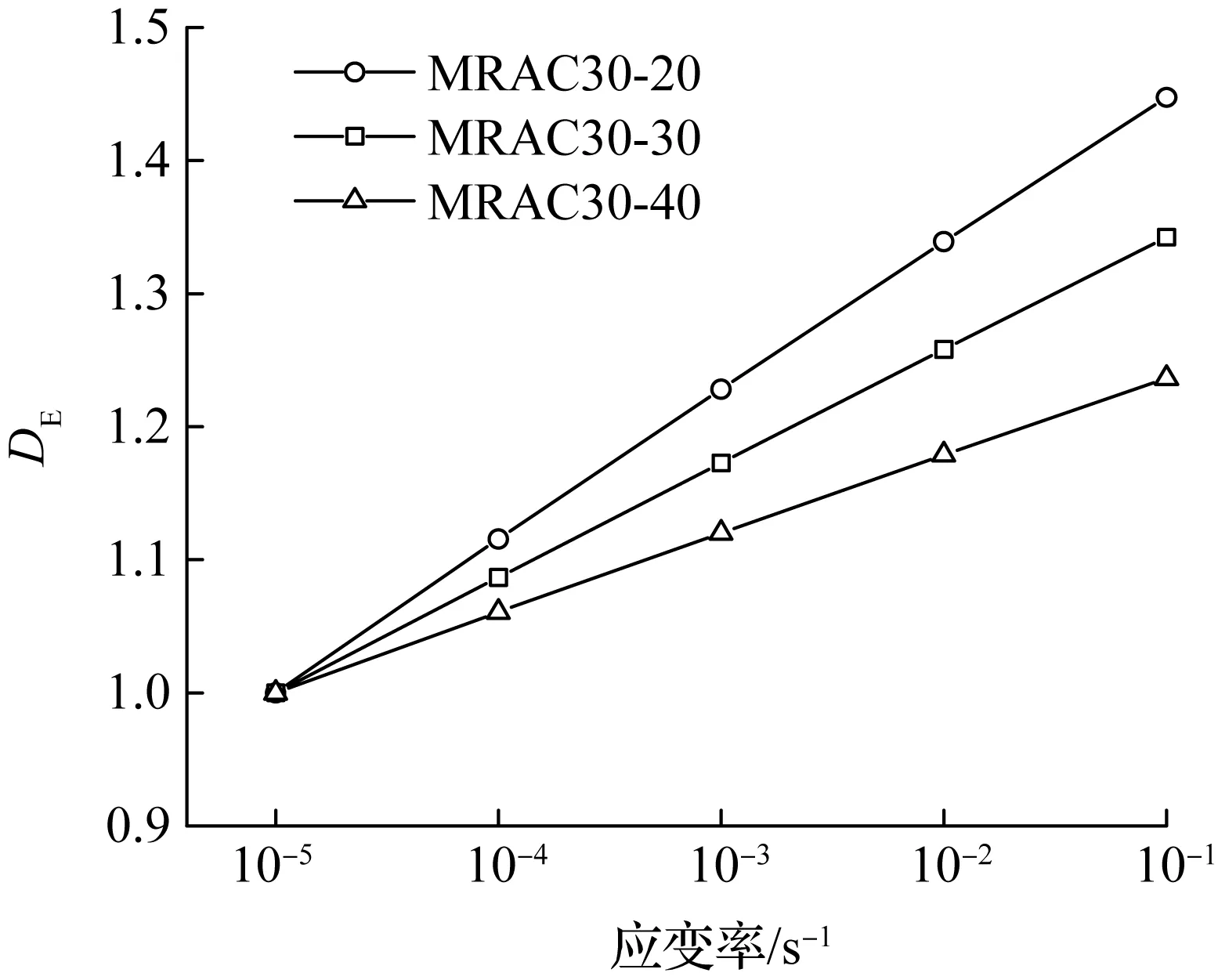
图11 不同新砂浆的再生混凝土的DE与应变率的关系

4.3 老砂浆强度的影响

4.3.1 老砂浆强度对峰值应力率敏感性的影响

不同老砂浆的再生混凝土的峰值应力Df与应变率的关系如图12所示．可发现,尽管MRAC20-30中老砂浆的率敏感性大于MRAC30-30中老砂浆的率敏感性,但整体的峰值应力率敏感性却略小于MRAC30-30．这说明再生混凝土的峰值应力率敏感性并非随着老砂浆率敏感性的增大而增大．本文认为新老砂浆相对强度可能也会影响其整体率敏感性．

图12 不同老砂浆的再生混凝土的Df与应变率的关系

4.3.2 老砂浆强度对弹性模量率敏感性的影响

不同老砂浆的再生混凝土的DE与应变率的关系如图13所示．结果表明,老砂浆强度越高,再生混凝土的DE增长越慢,即其弹性模量率敏感性越小,该特征与老砂浆强度对峰值应力率敏感性的影响有所不同．

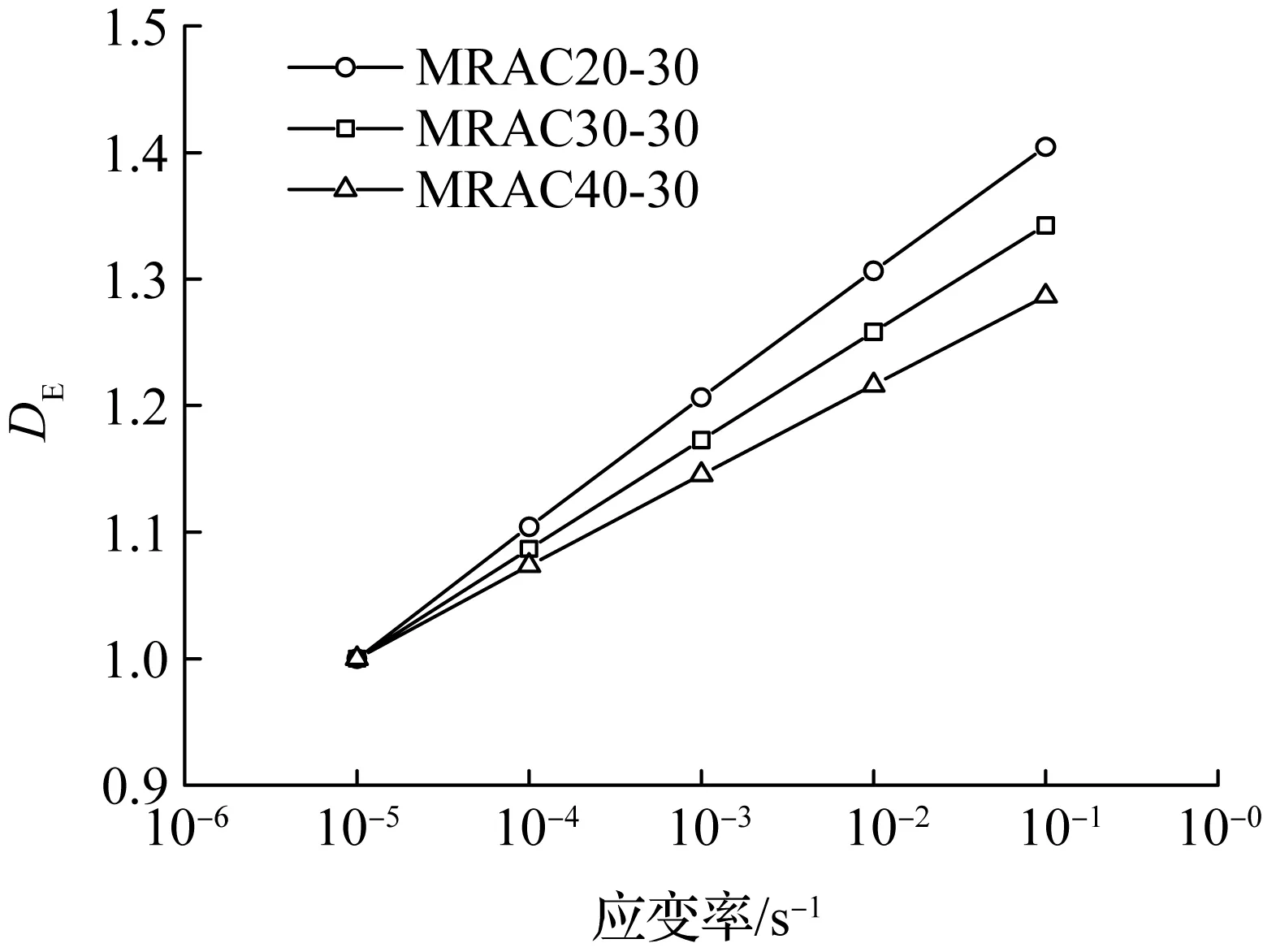
图13 不同老砂浆的再生混凝土的DE与应变率的关系

4.3.3 新、老砂浆强度的影响对比

图14和图15分别比较了改变新、老砂浆强度对再生混凝土试件的Df和DE的影响．由图可知,采用率敏感性较大的新砂浆时,再生混凝土DE的增长速度比采用率敏感性较大的老砂浆时更快,说明相对于老砂浆,新砂浆的率敏感性对整体弹性模量率敏感性的影响更加显著．然而,新、老砂浆对试件整体Df的影响程度孰重孰轻却没有一致的规律．总体而言,由于试件中新砂浆含量高于老砂浆,使得新砂浆对整体弹性模量率敏感性的影响程度更大,但是对整体峰值应力率敏感性的影响程度没有明确规律,这可能是因为影响试件整体峰值应力的因素比影响弹性模量的因素更复杂．

图14 新、老砂浆强度对再生混凝土的Df的影响比较

图15 新、老砂浆强度对再生混凝土的DE的影响比较

5 结果讨论

再生混凝土的弹性模量反映的是其初始阶段的变形特征,它可视作各细观相材料弹性模量的加权平均值,权值由各细观相材料的体积分数决定．因此,体积分数大的砂浆对再生混凝土弹性模量率敏感性起主导作用,体积分数小的界面过渡区对其的影响非常小;取代率越大时,再生混凝土中砂浆含量越高,而砂浆的率敏感性大于骨料,从而使得再生混凝土整体弹性模量率敏感性越大;采用率敏感性较高的新、老砂浆,再生混凝土整体弹性模量率敏感性也较大．这也是各参数改变时DE呈现均匀增长的原因．

根据李杰等[17]提出的混凝土随机本构模型,一个混凝土试件可简化为一个串并联弹簧系统,该系统由多个并联弹簧构成的损伤体串联而成．混凝土的强度由最弱损伤体单元的强度控制．因此,在再生混凝土试件中界面过渡区的体积分数虽小,但它们是试件整体的薄弱部位,决定着最弱损伤体单元的强度,所以界面过渡区的峰值应力提高时会对整体峰值应力有一定影响,故界面过渡区率敏感性对整体峰值应力率敏感性有一定影响．当混凝土试件的细观结构或各细观相材料的相对强度和变形能力发生变化时,混凝土试件的最弱损伤体单元也会发生变化,即它们会影响混凝土试件的整体强度．因此,当取代率增大时,虽然砂浆含量增大,但细观结构也在发生变化,使得再生混凝土试件峰值应力率敏感性与取代率并非呈现递增关系;虽然采用率敏感性较大的新、老砂浆,但此时细观相材料之间的相对强度也发生变化,从而使得再生混凝土试件峰值应力率敏感性并没有严格增大．

6 结论

1) 本文有限元模型可以较好地模拟再生混凝土的率敏感性,且模拟结果中也得到了与试验结果类似的规律:再生混凝土的峰值应力和弹性模量随着应变率的增大近乎线性增大,且弹性模量的增长更加均匀;峰值应变随应变率的增大没有明显变化．

2) 砂浆部分的率敏感性对再生混凝土整体的峰值应力和弹性模量率敏感性影响起主要作用,而界面过渡区和骨料部分的率敏感性对其影响较小．

3) 再生粗骨料取代率越大,再生混凝土弹性模量的率敏感性越大;再生粗骨料取代率为33%,55%,66%和100%的再生混凝土的峰值应力率敏感性差别不大,且均比普通混凝土高．

4) 随着新、老砂浆强度降低,再生混凝土的弹性模量率敏感性增大;而峰值应力率敏感性随新砂浆强度的降低而增大,随老砂浆强度的降低并未呈现增大趋势．

References)

[2]Etxeberria M, Vzquez E, Marí A, et al. Influence of amount of recycled coarse aggregates and production process on properties of recycled aggregate concrete[J].CementandConcreteResearch, 2007, 37(5): 735-742. DOI:10.1016/j.cemconres.2007.02.002.

[3]胡琼, 宋灿, 邹超英. 再生混凝土力学性能试验[J]. 哈尔滨工业大学学报, 2009, 41(4): 33-36. Hu Qiong, Song Can, Zou Chaoying. Experimental research on the mechanical properties of recycled concrete [J].JournalofHarbinInstituteofTechnology, 2009, 41(4): 33-36. (in Chinese)

[4]Xiao J Z, Li W G, Fan Y H, et al. An overview of study on recycled aggregate concrete in China (1996—2011)[J].ConstructionandBuildingMaterials, 2012, 31: 364-383. DOI:10.1016/j.conbuildmat.2011.12.074.

[5]Abrams D A.Effect of rate of application of load on the compressive strength of concrete [J].ASTMJournal, 1917, 17(2):70-78.

[6]Bischoff P H, Perry S H. Compressive behaviour of concrete at high strain-rates[J].MaterialsandStructures,1991, 24(6): 425-450. DOI:10.1007/bf02472016.

[7]Malvar L J, Ross C A. Review of strain-rate effects of concrete in tension [J].ACIMaterialsJournal, 1998, 95(6): 735-739.

[8]Lu Y B, Chen X, Teng X, et al. Dynamic compressive behavior of recycled aggregate concrete based on split Hopkinson pressure bar tests[J].LatinAmericanJournalofSolidsandStructures, 2014, 11(1): 131-141. DOI:10.1590/s1679-78252014000100008.

[9]Rao M C, Bhattacharyya S K, Barai S V. Behaviour of recycled aggregate concrete under drop weight impact load[J].ConstructionandBuildingMaterials, 2011, 25(1): 69-80. DOI:10.1016/j.conbuildmat.2010.06.055.

[10]Xiao J Z, Li L, Shen L M, et al. Compressive behaviour of recycled aggregate concrete under impact loading[J].CementandConcreteResearch, 2015, 71: 46-55. DOI:10.1016/j.cemconres.2015.01.014.

[11]Li L, Xiao J Z, Poon C S. Dynamic compressive behavior of recycled aggregate concrete[J].MaterialsandStructures, 2016, 49(11): 4451-4462. DOI:10.1617/s11527-016-0800-1.

[12]肖建庄,袁俊强,李龙. 模型再生混凝土单轴受压动态力学特性试验[J].建筑结构学报,2014,35(3): 201-207. Xiao Jianzhuang, Yuan Junqiang, Li Long. Experimental study on dynamic mechanical behavior of modeled recycled aggregate concrete under uniaxial compression [J].JournalofBuildingStructures, 2014, 35(3): 201-207. (in Chinese)

[13]Xiao J Z, Li W G, Corr D J, et al. Simulation study on the stress distribution in modeled recycled aggregate concrete under uniaxial compression [J].JournalofMaterialsinCivilEngineering, 2013, 25(4): 504-518. DOI:10.1061/(asce)mt.1943-5533.0000598.

[14]翟越, 马国伟, 赵均海, 等. 花岗岩和混凝土在单轴冲击压缩荷载下的动态性能比较[J]. 岩石力学与工程学报, 2007, 26(4): 762-768. DOI:10.3321/j.issn:1000-6915.2007.04.015. Zhai Yue, Ma Guowei, Zhao Junhai, et al. Comparison of dynamic capabilities of granite and concrete under uniaxial impact compressive loading[J].ChineseJournalofRockMechanicsandEngineering, 2007, 26(4): 762-768. DOI:10.3321/j.issn:1000-6915.2007.04.015.(in Chinese)

[15]肖建庄, 黄凯文, 李龙. 模型再生混凝土单轴受压静力与疲劳性能数值仿真[J].东南大学学报(自然科学版), 2016, 46(3): 552-558. Xiao Jianzhuang, Huang Kaiwen, Li Long. Numerical simulation on static force and fatigue behaviors of modeled recycled aggregate concrete under uniaxial compression [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2016, 46(3): 552-558.(in Chinese)

[16]Comité Euro-international du Béton. CEB-FIP model code 1990 [S]. London: Thomas Thelford, 1993.

[17]李杰, 张其云. 混凝土随机损伤本构关系[J]. 同济大学学报(自然科学版), 2001, 29(10): 1135-1141. DOI:10.3321/j.issn:0253-374X.2001.10.001. Li Jie, Zhang Qiyun. Study of stochastic damage constitutive relationship for concrete material[J].JournalofTongjiUniversity(NaturalScience), 2001, 29(10): 1135-1141. DOI:10.3321/j.issn:0253-374X.2001.10.001.(in Chinese)

Numerical simulation on strain-rate sensitivity of mechanical properties of recycled aggregate concrete

Li Long1,2Xiao Jianzhuang1Huang Kaiwen1

(1College of Civil Engineering, Tongji University, Shanghai 200092, China) (2Faculty of Construction and Environment, The Hong Kong Polytechnic University, Hong Kong 999000, China)

A finite element model based on the modeled recycled aggregate concrete with nine aggregates is established. The strain-rate sensitivity of mechanical properties of recycled aggregate concrete (RAC) and the influence of the strain-rate sensitivity of each meso-phase material on it are studied. The effects of the recycled coarse aggregate (RCA) replacement ratio and the strength of new mortar or old mortar on the overall strain-rate sensitivity of RAC are discussed. The simulation results show that the finite element model can simulate the strain-rate sensitivity of RAC well. The peak stress and elastic modulus of RAC increase almost linearly with the increase of strain-rate, and the increasing rate of elastic modulus is more uniform. Compared with aggregate and interfacial transition zone, the strain-rate sensitivity of RAC is mainly influenced by the strain-rate sensitivity of mortar in RAC. When the RCA replacement ratio increases or the strength of new mortar or old mortar decreases, the strain-rate sensitivity of elastic modulus of RAC increases, but the influences of these factors on the strain-rate sensitivity of peak stress of RAC are different.

recycled aggregate concrete (RAC); mechanical property; strain-rate sensitivity; numerical simulation; recycled coarse aggregate (RCA) replacement ratio

10.3969/j.issn.1001-0505.2017.04.023

2016-12-20. 作者简介: 李龙(1988—)，男，博士；肖建庄(联系人)，男，博士，教授，博士生导师，jzx@tongji.edu.cn.

国家杰出青年科学基金资助项目(51325802).

李龙,肖建庄,黄凯文.再生混凝土力学性能的应变率敏感性数值模拟[J].东南大学学报(自然科学版),2017,47(4):776-784.

10.3969/j.issn.1001-0505.2017.04.023.

TU528.59

A

1001-0505(2017)04-0776-09