基于“最值”问题，开展变式教学

贾林

[摘 要] 新课标大纲注重问题的变式探究，变式问题的本质是围绕教材的基本概念和原理开展的，这对教师的教学备课提出了更高的要求，筆者认为作为教师有必要围绕教学内容进行设计和变式教学，提升学生的探究能力. 本文整理了最近的一次关于“解析几何最值问题”的教学设计，与同行研讨.

[关键词] 解析几何；最值；变式探究

解析几何的最值问题是教材内容的变式拓展，在考题中出现的频次很高，考查学生的变式探究能力，这也是当下课改的主体思想，作为教师也需要关注变式问题，并以此进行教学设计，围绕相关的问题开展变式教学，培养学生的变式思维.

[?] 教学流程

1. 问题引入

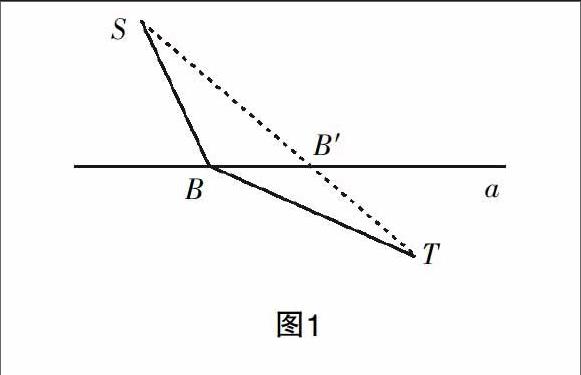
在公路a两旁有两所学校S和T，现将要在公路上建一个公交站台B，让两所学校的学生到这个站台的距离之和为最小，现设计该站台的具体位置，并说出理由.

预设问题：解决最值问题的基本原理是什么？两点之间线段最短如何证明？有人提出应该放在三角形中进行求解，你是如何思考的？

预设意图：本节主要学习解析几何中的最值问题，通过生活中的实际问题，让学生对最值问题有个初步的认识，理解最值问题的基本原理，然后以此为线索开展课题，提高学生的学习兴趣，以学生为教学的主体，这样的设计有助于培养学生的思考能力，以及变式思维，为今后的教学做准备.

探究：当定点S和T位于动点所在直线的异侧时可求距离之和，解决最值问题，可以根据原理：两点之间线段最短，证明上可借助三角形的两边之和不小于第三边.

解析：如图1所示，连接直线ST，线段ST和直线a的交点为B′，在直线a上任取一点B，则根据三角形边的关系有：SB+TB≥ST，所以SB+TB的最小值就是线段ST的长度.

[?] 典例讲评与变式

预设问题：动点M和N的轨迹是什么样的曲线？如果当点P静止的时候，线段PM和PN的大小有联系吗？求PM+PN的最小值，是否可以实现PM和PN都达到最小值？

预设意图：由生活中的最值问题转化为解析几何中常见的求解动点的最值问题，通过逐步的设问来引导学生培养正确的解题思路，这里以圆上的动点为例，引导学生进行数形结合，通过分析判断求解最值问题的特定情形.

（3）经过点F1（-2，0）作两条互相垂直的直线，直线分别交椭圆C于A，B和D，E点，求AB+DE的最小值.

设计意图：经过对解析几何最值问题的基础讲解以及变式后，有必要对学生进行视野拓展，通过对高考历年真题的赏析使学生深入理解解析几何中的最值问题的考查要求，扎实基础，进一步提升综合解题能力.

[?] 教学立意的进一步解读

1. 重视概念，重视原理

学习概念和数学原理是求解问题的基础，在理解原理的基础上才可以实现变式拓展，例如题课中关于最值问题，两点之间线段最短则是最值问题的理论依据. 在教学过程中不可忽视数学概念的教学，即使是原本枯燥无味的概念原理课，通过精心的课程设计也可以变得生动，在教授过程中要有准备有意识地引导学生去发现、创造，笔者认为新课标更应该注重教材的原理和概念教学，重视问题的外延本源，从问题的出发点进行教学更加有利于学生掌握基础，拓展变式. 在讲授解析几何问题时要研究曲线的性质以及求解方法的原理. 解题的步骤是：作图、分析、化简、求解. 问题的产生和发展都应以教材的概念和原理作为载体，所以课堂教学必须以教材的基础知识作为出发点.

2. 探究问题，拓展变式

解析几何的问题都可以在教材中找到原理依据，仅对一道例题的讲解是无法使学生掌握原理，理解教材概念的. 特别是解题背后所蕴含的数学思想和方法技巧，所以对于教材的探究则变得非常重要. 在本节课的教学环节进行了典题变式和衔接高考真题，都是为了使学生在理解最值的基础上进行深入探究，在训练中抓住问题的本质，理解高考命题策略. 对问题的拓展，都是对问题的进一步解读和探索；对新问题的思考，将问题的条件和结论进行类比和联想，都可以使学生产生新的解题思路，这是变式的核心内容. 探索问题的过程是一种发掘的过程，可以彻底地理解课本原理，拓展学生的思维，提升解题能力.

3. 系统思考，总结归纳

问题的产生是一个系统的过程，所以解题的目的也是为了通过思考分析，层层推进，形成一个系统的思维体系. 在教学过程中，教师要善于利用教学资源，让学生以一个研究者的身份去思考问题，敏锐观察，系统归纳，让教学成为一个系统探究的过程. 教师要让学生学会总结归纳，发现问题的内在联系，学会从不同的角度进行分析和综合，从整体上把握解题思路，只有从整体出发，进行的创作认知才可以透过问题的表象深入精髓. 在数学解题中要鼓励学生去深入探究，每一次思考都是一次成功的探究，每一次总结归纳都可以获得思维上的提升，让学生学会系统的思考才是教学的重点.

[?] 写在最后

教学设计是教师能力的体现，一堂好的教学课可以使学生在理解基本知识的基础上，获得探究能力的提升，对于解析几何的相关问题，笔者认为应该落实到课堂中，每一次课堂讲授都值得精心设计.