圆锥滚子无心贯穿式超精研中滚子滑动分析
贾松阳,马有福,时可可,师金台,高鹏飞
(1.洛阳LYC轴承有限公司,河南 洛阳 471039;2.航空精密轴承国家重点试验室,河南 洛阳 471039)
近年来,高性能轴承受到重视,其中高精度圆锥滚子的加工质量成为制约我国高性能轴承制造质量的瓶颈之一[1-2]。无心贯穿式超精研是目前普遍使用的圆锥滚子凸度加工工艺,对圆锥滚子的表面质量与加工精度有着决定性影响,其能在几秒至几十秒内,把滚子表面粗糙度值由0.63~0.16μm减小到0.08~0.01μm,使装配后的轴承噪声明显降低,旋转精度和寿命可靠性均有较大幅度地提高[3-5]。圆锥滚子无心超精研加工中,滚子由2个同向旋转的导辊带动旋转和移动,依次通过不同粒度和硬度的振荡油石;前后油石以不同压紧力作用于滚子表面对其进行研磨加工。根据滚子需求的凸度形状不同,可分为导辊工作面角度相同的直进式超精和角度不同的斜进式超精。
超精导辊是结构复杂技术含量高的工装,其廓形为复杂空间曲面的组合,对精加工和修磨技术要求很高[6-7]。在导辊驱动滚子运动过程中会出现滚子轴向滑动[8],同时,导辊依靠摩擦力驱动圆锥滚子旋转,其形式是摩擦传动,不可避免也会出现圆周方向的滑动现象。这种轴向和周向滑动势必导致导辊的磨损。试验结果表明,在加工铁路客车轴承滚子时,导辊大约1个月就需要修磨1次,修磨时间增加了滚子成本[9]。因此,面对日益严峻的追求低成本和高精度的市场形势,有必要分析无心贯穿式超精研中导辊与滚子之间的滑动现象。
目前缺少导辊与滚子间滑动问题的相关研究。文献[8]阐述了一种利用丝表测试及微调导辊来降低滚子不稳定性的方法,该方法有助于减少轴向滑动造成的圆锥滚子旋转不稳定,从而提高加工精度。文献[10]从滚子扭矩角度分析了导辊接触角对滚子旋转运动稳定性的影响,在分析滚子转速时,滑动系数取值为0.9,但未说明取值原因或来源。因此,现对无心贯穿式超精研滑动问题中的周向滑动问题进行探讨,对减少导辊磨损和提高滚子加工质量有一定工程借鉴意义。
1 导辊与滚子间的周向滑动类型
无心贯穿式超精研中,导辊依靠摩擦力驱动圆锥滚子旋转,理想情况是滚子匀速旋转,使其圆周面能均匀得到油石的超精加工。但实际上,摩擦传动存在周向滑动现象,其滑动可分为弹性滑动、几何滑动和打滑[11-12]。
1.1 弹性滑动
导辊与滚子截面弹性滑动如图1所示。由于材料的弹性变形,导辊与滚子形成一个很小的面接触(接触区),摩擦力Ft的方向在滚子接触面上与滚子线速度方向相同,在导辊的接触面上与导辊线速度相反。在压力和摩擦力的综合作用下,接触区内导辊的表面金属层由进口处的压缩变形过渡到出口处的拉伸变形;滚子的表面金属层则相反,由进口处的拉伸变形过渡到出口处的压缩变形。由于接触区这2种方向相反的弹性形变变化过程,使导辊与滚子表面在接触区产生相对滑动,弹性滑动会导致滚子的速度损失。钢-钢的滑动系数约为0.2%[13]。
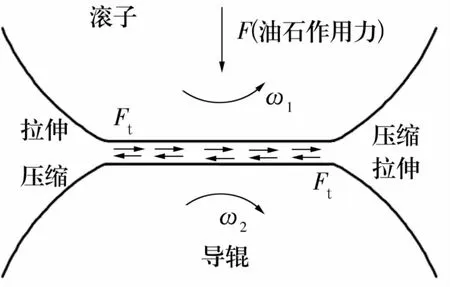
图1 圆锥滚子的弹性滑动Fig.1 Elastic sliding of tapered roller
由于导辊与滚子材料的弹性模量都很大,而接触压力又比较小,因此弹性滑动的影响甚小,可忽略不计。这里仅作简要介绍和说明,不作重点研究。
1.2 几何滑动
由于传动副几何形状及相对位置等因素引起的滑动称为几何滑动。几何滑动的大小一方面由接触线的形状决定,另一方面由某些运动和结构参数决定[14]。导辊与滚子的廓形都是复杂的锥形面,其摩擦传动形式与一般的圆筒形摩擦传动显然是不同的。这种特殊的锥形几何形状会导致几何滑动,因此,高精度圆锥滚子的加工不能忽视该问题。
1.3 打滑
摩擦传动中,当载荷过大以至于超过最大摩擦力时将产生打滑;此外,传动件接触点处线速度的大小或方向不同也会导致打滑。圆锥滚子无心贯穿式超精研中,滚子受到导辊的支承力、摩擦力及油石的压力、研磨力,滚子贯穿研磨全过程,要通过4~6块压力不等、粒度和硬度不同的振荡油石,压力和研磨力都将发生变化,导辊的支承力和摩擦力也会随之发生变化;滚子贯穿单个油石的过程中,油石的振荡作用使研磨力方向动态变化。目前尚未见到对油石研磨力计算方面的研究,因此,分析导辊与滚子之间的打滑现象十分困难。
1.4 小结
综上可知,弹性滑动影响甚小,限于滚子受力情况的复杂,打滑现象的分析存在困难。因此,文中将重点对几何滑动展开分析。
2 导辊与滚子间的几何滑动
圆锥滚子无心贯穿式超精研中,导辊与滚子的复杂锥形几何特征导致了几何滑动。
2.1 导辊与滚子的几何接触形状
导辊辊形对圆锥滚子超精研加工质量有显著影响。由文献[5]可知,目前国内对导辊辊形进行了大量的研究,在不同的简化条件下,采用不同的数学方法得到了不同的工作面表达式,均表示导辊工作面的轴向截形是一条复杂的内凹曲线,如图2所示。
图2中α和β分别为圆锥滚子和导辊的半锥角。β是导辊形面设计的重要参数,有多种计算方法,文献[6]根据多年实践总结的简化经验公式,更适合现场计算使用,
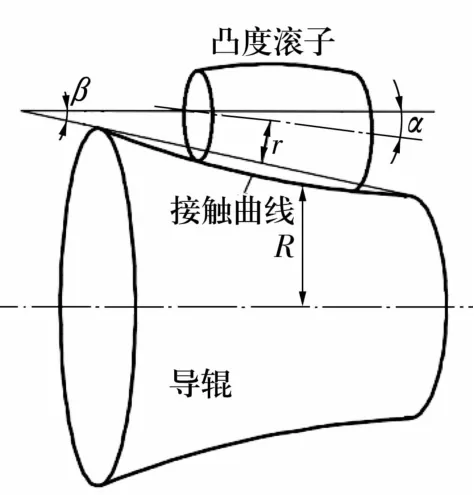
图2 导辊和圆锥滚子的接触曲线Fig.2 Contact curve of guide roller and tapered roller
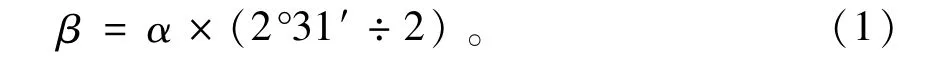
导辊的设计十分复杂,涉及很多参数,因其对分析几何滑动关系不大,这里不深入展开。
导辊以一定的角速度ω2驱动滚子以角速度ω1回转,由于导辊(或滚子)在接触线范围内各处半径的不同,其接触线上的线速度不同,导致了几何滑动的发生。
2.2 导辊与滚子几何滑动建模
由于导辊辊形曲线的计算方程十分复杂,将会加大几何滑动的分析难度,为方便建模,将导辊与滚子的轮廓线都简化为直线,而不是带凸度曲线,这也是很多导辊设计和修磨经常采用的简化计算方法。如图3所示,圆锥滚子绕中心轴Ⅰ旋转,角速度为ω1;导辊沿轴线Ⅱ旋转,角速度为ω2。圆锥滚子的小端半径为r1,导辊上对应滚子小端的初始半径为R1,L为滚子长度。
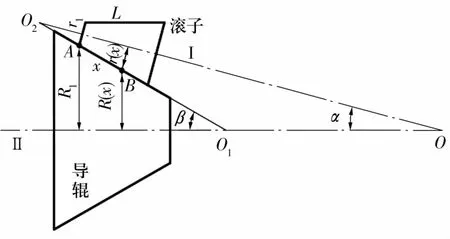
图3 圆锥滚子几何滑动分析图Fig.3 Analysis diagram of geometric sliding of tapered roller
假设接触线起点为A点,距离起点为x的B点对应的圆锥滚子半径可表示为

则滚子上任意点的线速度v1(x)可表示为
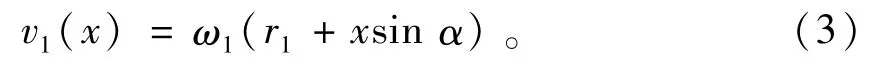
同理可得B点对应的导辊半径R(x)及线速度v2(x)为
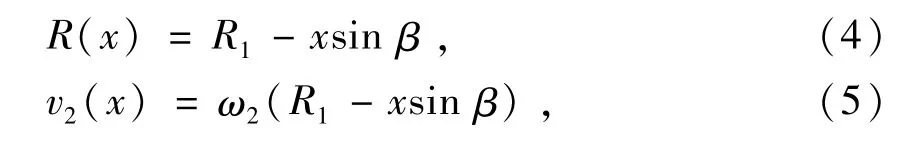
以上x∈[0,L]。
由(3),(5)式可知,接触线上滚子的速度是关于x的线性增函数,导辊的速度是关于x的线性减函数。如图4所示,在接触线上的某一点处,滚子线速度v1(a)等于导辊线速度v2(a),而其他各点处均不相等,即存在几何滑动,且在相等点两侧滑动速度分布方向相反。称此速度相等点为纯滚动点,即
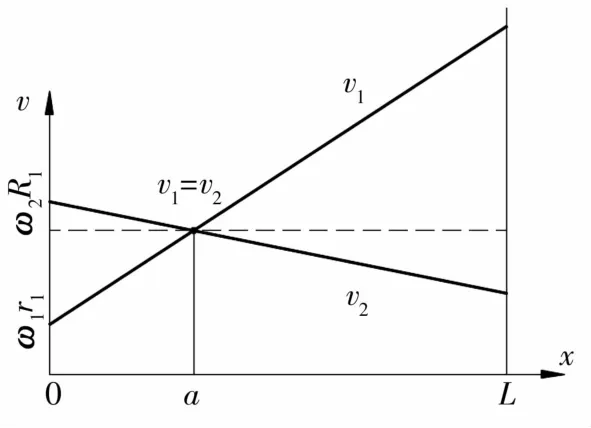
图4 圆锥滚子与导辊的线速度Fig.4 Linear velocity of tapered roller and guide roller

将(3),(5)式代入(6)式,整理得到导辊与滚子角速度关系式为
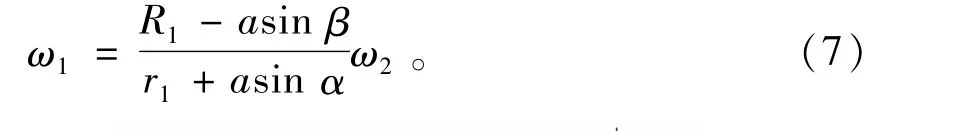
理想情况下,在接触线上导辊与滚子运动应同步,即线速度应相等,但实际情况是存在差值而且不同位置差值不相等。从评估滑动对导辊磨损的影响这一角度看,可以认为导辊与滚子接触线上的线速度差值之和最小时,导辊磨损最小。因此目标函数可表示为
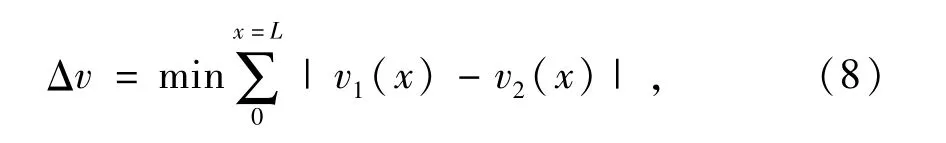
式中:Δv为导辊与滚子在接触线上各位置线速度差值的和。为简化计算,认为接触长度和圆锥滚子长度相等(实际差值很小,可忽略)。
因各参数代入(8)式后计算分析困难,从图3可知,可将其等价转换为v1(x)和v2(x)所夹面积之和,用S表示。因此,从几何关系上,几何滑动的目标函数可表示为
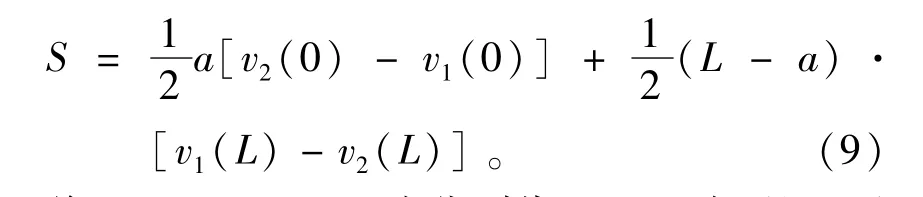
将(3),(5),(7)式分别代入(9)式,整理后得到几何滑动目标函数为
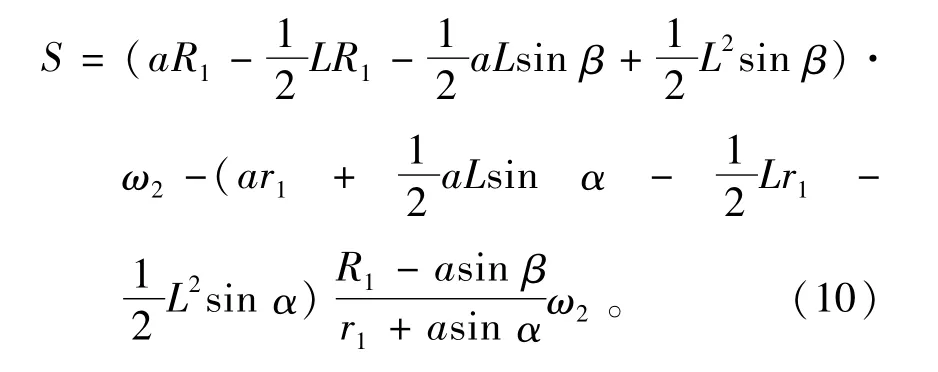
2.3 导辊与滚子几何滑动的分析
在给定圆锥滚子时,(10)式中可变参数为导辊半径R1、导辊转速ω2和纯滚动点位置a;另外,滚子锥角是引起几何滑动的根本原因。因此,对这些参数进行分析。
2.3.1 纯滚动点的最优位置
由(7)式可知,在纯滚动点位置,导辊与滚子转速符合一定传动比。反言之,若已知导辊与滚子转速就能计算出纯滚动点的位置。导辊的转速可以主动调整确定,而滚子的转速是依靠摩擦力被动形成的,可见纯滚动点位置和滚子转速是互为已知条件而计算得到的。实际上,由于加工中各种因素的影响,滚子的转速可能存在微小的变化,需根据具体情况实际检测滚子的转速,因此,单从理论上无法确定滚子转速,也就无法计算纯滚动点的实际位置。
虽然无法理论确定纯滚动点的实际位置,根据(10)式,对a求导,则可以得出纯滚动点的最优位置。

整理化简后得
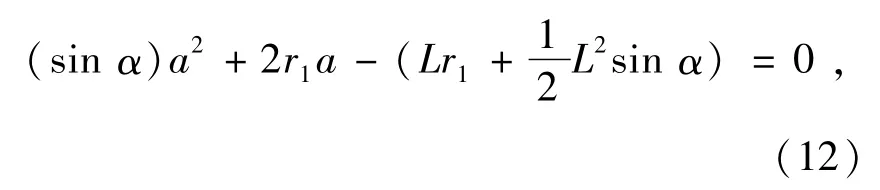
从而解得纯滚动点位置a的最优位置计算方程为
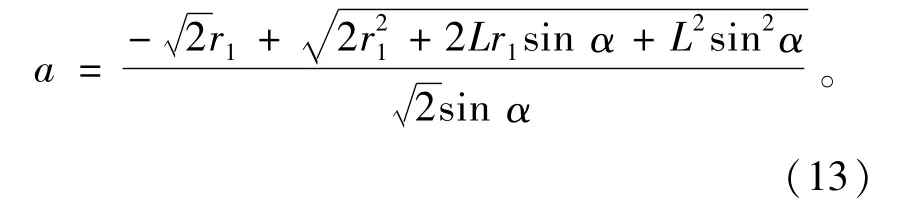
在给定圆锥滚子形状参数:α=2°,L=48 mm,r1=16 mm下,将导辊转速和半径分别固定为60 rad/s和80 mm,由(1)式计算得β=2°31′,由(13)式计算出的最优纯滚动点位置为a=24.6 mm。将纯滚动点设置为a=0~48 mm,基于(10)式绘制出的几何滑动变化情况如图5所示。
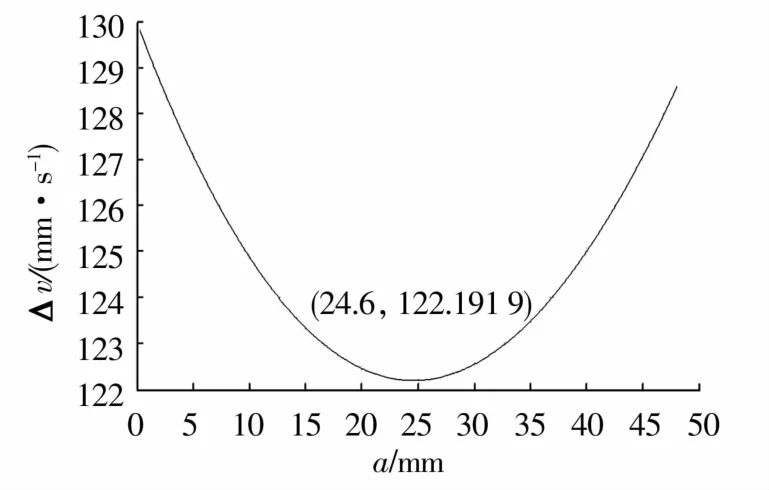
图5 纯滚动点位置对几何滑动的影响Fig.5 Influence of position of pure rolling point on geometric sliding
由以上分析可知,纯滚动点位于由(13)式确定的位置时,总的几何滑动最小,此时应是最优情况。由于纯滚动点的实际位置未知,因此实际中对纯滚动点位置控制的问题有待进一步实践、研究。
2.3.2 导辊半径和转速对几何滑动的影响
滚子参数不变,取纯滚动点在最优位置即a=24.6 mm;设置导辊转速ω2=20~100 rad/s,导辊半径R1=20~100 mm,计算出的几何滑动变化情况如图6所示。
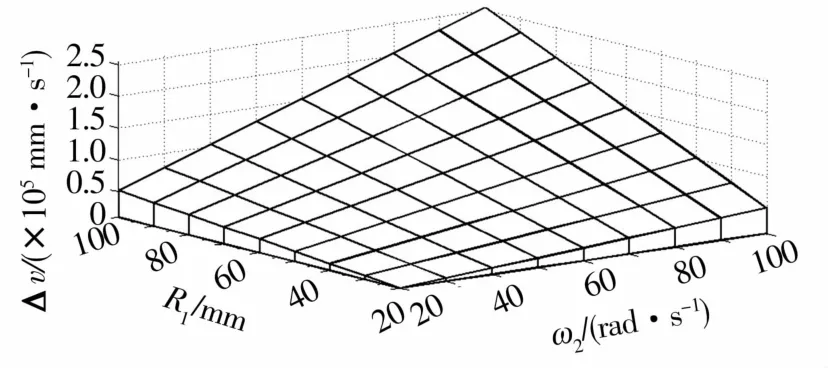
图6 导辊半径R1和转速ω对几何滑动的影响Fig.6 Influence of guide roller radius R1 and rotational speed ωon geometric sliding
由图可知,在导辊转速和导辊半径逐渐增大的过程中,几何滑动都表现出逐渐增大的趋势。不管是单因素还是2个因素的综合作用,导辊转速和半径都与几何滑动正相关。
2.3.3 导辊设计应注意的问题
在导辊设计时,导辊半径的确定方法如下

式中:T为导辊螺距,mm;d为滚子的小端直径,mm;Lw为导辊有效长度(即油石下的长度),mm;L为滚子长度,mm;B为导辊挡边厚度,一般取4~6 mm。
由(7)式可知滚子转动速度ω1由纯滚动点处导辊与滚子的半径及导辊的转速确定。综上,在给定滚子的情况下,导辊的半径最终由自身在使用中的转速和纯滚动点位置决定。纯滚动点位置是未知和不可控因素,转速则是根据实践经验确定的。若采取的导辊转速越大,导辊设计半径也就越大,加工中造成的几何滑动也越大,所以实践过程中,要选择合适的导辊转速用以设计导辊和控制滚子加工过程中的滑动。转速高虽能加大滚子贯穿速度,提高加工效率,但同时也会加大滚子几何滑动,影响滚子质量和加快导辊的磨损。
2.3.4 滚子锥角对几何滑动的影响
将圆锥滚子半锥角设置为α=2°~30°,导辊转速和半径分别固定为60 rad/s和80 mm。由(1),(13)式分别确定导辊半锥角β和纯滚动点最优位置a,计算得几何滑动变化趋势如图7所示。
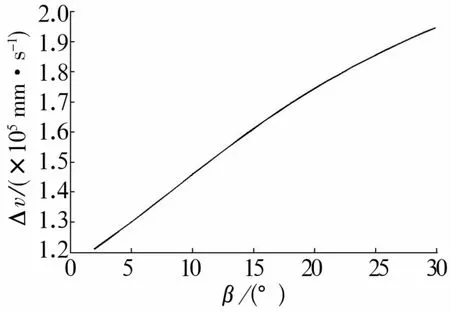
图7 圆锥滚子锥角对几何滑动的影响Fig.7 Influence of taper angle of tapered roller on geometric sliding
由图可知,滚子锥角越大,几何滑动越大,越不利于加工后的滚子表面质量,加快导辊的磨损。因此,在实践中对大锥角圆锥滚子的超精更应加强控制。
3 结论
1)给出了几何滑动最优化方程,并得到纯滚动点最优位置计算方程。纯滚点在最优位置时,几何滑动最小,但纯滚动点实际位置的控制有待研究。
2)导辊转速和导辊半径越大,导辊和圆锥滚子之间的几何滑动越大。在导辊设计时,应综合加工效率尽量选取较小的导辊转速参与计算,以减小几何滑动,提高加工质量,减少导辊磨损。
3)圆锥滚子锥角越大导致的几何滑动越大,实践中应加强大锥角圆锥滚子超精过程的滑动控制。

