基于改进人工蜂群的轴承故障诊断方法

薛勇，万振刚

(江苏科技大学 电子信息学院，江苏 镇江 212003)

滚动轴承在机械设备中的安装位置特殊，故障表征不明显，通过表面现象及简单的分析手段难以对轴承早期故障做出有效判断。为了对轴承早期故障进行有效识别，需要采用一定的算法对故障数据进行有效的分类和提取。人工蜂群算法是一种群体智能算法[1]，具有自组织性和自适应性，且具有搜索速度快、参数少、易于实现等优点，已成功应用于故障诊断、图像处理等领域[2-3]。

但人工蜂群算法在实际应用中存在易陷入局部最优，后期收敛效率低等问题。为了克服人工蜂群在识别过程中存在随机性、收敛速度慢、相似性匹配全局搜索能力差等问题，对人工蜂群算法进行了改进，通过组合权重的方式获取新的目标函数，从而进行人工蜂群全局性搜索，并可在搜索过程中通过均值法提高目标函数的收敛速率及稳定性，以增强故障诊断的效果。

1 故障分析理论

1.1 小波包熵特征提取

滚动轴承存在不同故障时，其振动信号在不同频带上的能量分布会有所不同，可根据各频带能量特征的差异性进行故障识别。小波包变换能够将时域中不易分辨的信息转换到频域上，并保持信息的完整性[4-5]。小波包熵提取的具体步骤为:

1)对原始信号进行4层小波包分解，获取16个频带上的信号特征。

2)求取16个频带上信号的能量，设X4j为对应频带中的重构信号，则其能量为

(1)

3)对得到的各能量进行归一化，即

(2)

4)计算各频带的能量熵P，作为待识别的故障特征值，P即人工蜂群算法中的引领蜂。

Pj=-TjlogTj。

(3)

1.2 人工蜂群算法

人工蜂群算法[6]一种群体智能优化算法，蜜蜂采蜜过程的主要组成要素包括：蜜源、引领蜂、跟随蜂和侦察蜂，引领蜂和跟随蜂开采蜜源，侦察蜂开辟新蜜源，帮助该算法跳出局部最优。蜜蜂采蜜即一种寻找最优解的过程。该过程中，假设有N个蜜源{x1,x2,…,xN}，每个蜜源xi(i=1,2,…,N)就是一个d维向量。

蜂群初始化后，整个蜂群进行引领蜂、跟随蜂和侦察蜂搜索过程的循环，直到达到最大迭代次数M或误差允许值u。具体搜索过程如下：

1)搜索开始阶段，引领蜂依据(4)式进行蜜源位置更新，即

vi,j=xi,j+λi,j(xi,j-xk,j)，

(4)

式中：k为随机产生的整数，k∈{1,2,…,N}，且j∈{1,2,…,d}；λi,j为[-1,1]之间的随机数。

2)引领蜂完成搜索后，将蜜源位置等信息与跟随蜂分享，跟随蜂通过这些分享信息判断蜜源的收益率，并根据收益率的大小选择采蜜的位置，适应度值为

(5)

式中：fi为第i个解的适应度值。

在人工蜂群算法中，设待优化目标函数为f(x)，若优化为最小值问题，则适应度函数为f(x)的变形，即

(6)

在人工蜂群算法中，Limit参数用于记录某个解未被更新的次数，通过L次循环之后仍未寻找最优解，则表明该解陷入局部最优，则该位置被舍弃，引领蜂则转变为侦察蜂。

2 改进的人工蜂群算法

作为一种群体优化算法，人工蜂群算法具有全局搜索能力强、识别准确度高、操作简便的特点，用于轴承故障的分析时可提高故障诊断的效率和准确性。但原始人工蜂群算法存在收敛速度慢、随机性高等问题，因此，提出了一种改进的人工蜂群算法，通过优化相似性匹配函数的方式对目标函数进行改进，通过改变迭代更新目标位置的方式克服原始人工蜂群算法中寻优目标位置选取的随机性，加快了收敛速度，丰富了共享信息内容，并充分发挥了人工蜂群全局寻优能力强的特点，大大提高了故障诊断的正确率。

基于改进人工蜂群算法的滚动轴承故障诊断流程如下：

1)计算轴承振动信号的小波包能量熵，提取特征向量。

2)采用Minkowski距离[7]和Pearson相关系数[8]相结合的方式对目标函数进行优化。通过计算匹配过程中2种算法的影响因子进行权重分配，确定目标函数。设Minkowski距离权重为a，Pearson相关系数权重为b，则

(7)

(8)

式中：S1，S2分别为Minkowski距离和Parson相似性系数的可区分度。综合2种距离测度方法得到最终相似性测度为

Z(xi,xj)=aD(xi,xj)+b[1-M(xi,xj)]，

(9)

式中：D(xi,xj)为Minkowski距离；M(xi,xj)为Pearson相似性系数。

3)蜂群搜索开始阶段，将蜜蜂分为引领蜂和跟随蜂，引领蜂通过目标函数寻找优质蜜源，即相似性匹配，以(9)式为目标函数寻找匹配适应度最大的蜜源位置，并将该蜜源的位置、含蜜量(适应度值)等信息分享给跟随蜂；跟随蜂通过分享信息确定各蜜源的收益率及位置，采用求特征向量与最优解向量均值[9]的方式对蜜源位置进行逐次迭代更新，直到满足最大迭代次数或误差小于限定值时，确定适应度大小及最优位置信息{fi, [x1,x2,…,xN]}。

4)根据适应度大小确定最终数据分类后所属的类型，若经过L次循环仍未寻找到优质蜜源，则放弃该蜜源，重新开辟新的蜜源位置，即寻找新的特征聚类中心。

3 试验分析

试验数据来源于凯斯西储大学轴承数据中心，故障模拟平台包括驱动电动机，扭矩传感器，功率计以及电子控制设备。测试数据来自驱动端轴承SKF6205，采用电火花加工的单点损伤模拟故障，故障直径为0.533 4 mm，转速1 797 r/min，采样频率为12 kHz，对轴承4种工作状态下(内圈故障、外圈故障、钢球故障和正常状态)的加速度信号分别采样，每种状态采样11组(第1组无故障状态数据作为模板数据，其余10组作为试验数据)，共计41组数据，每组200个数据点。

试验开始阶段，首先对振动信号进行小波包变换，提取振动信号在16个不同频带上小波包熵特征值，以16个频带的熵值作为特征向量进行相似性测度匹配。4种状态下振动信号的各频带能量熵如图1所示。

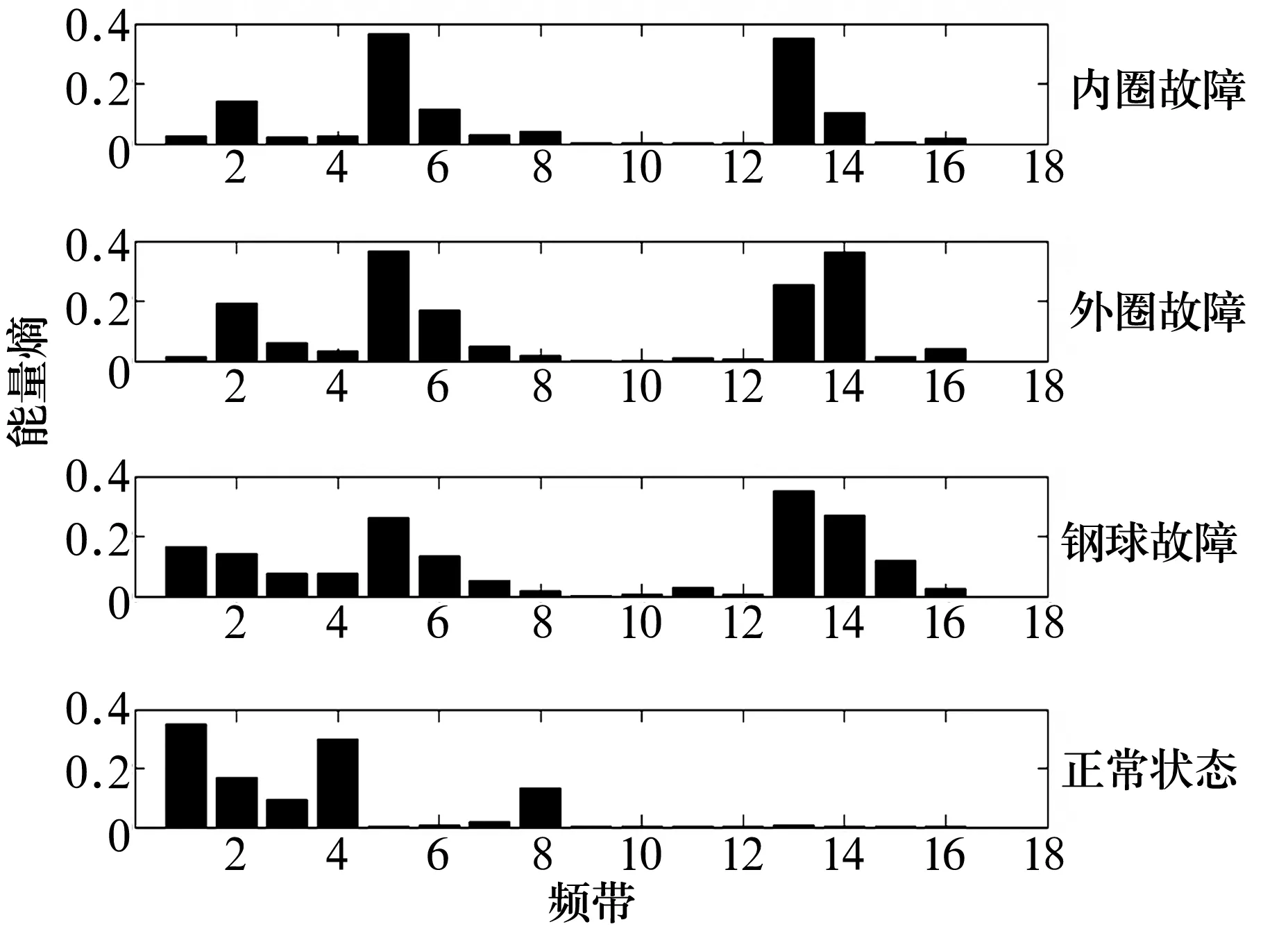
图1 各频带能量熵分布Fig.1 Energy entropy distribution on each frequency

从图1可以看出，不同状态振动信号的特征值在整体分布上存在明显的差异：内圈故障主要分布在5,13频带上,外圈故障主要分布在5,13,14频带上,钢球故障主要分布在1,5,13,14频带上,而正常状态数据主要分布在1,4频带；由不同频带上的特征值所组成的特征向量存在距离或角度上的差异性,通过相似性特征匹配可以反映出轴承存在的早期故障。

通过数据之间的相似性可以判断其所属类别，而相似性可以通过类内距离表示。试验中，采用第1组无故障数据对4种状态进行相似性识别，当相似性距离测度大于0.7时为故障状态，相似性距离测度小于0.1时为正常状态，当相似性测度在0.1～0.7之间时则为待识别状态。

为证明改进人工蜂群算法在故障识别上的优越性，采取欧氏距离相似性测度匹配作为对比，对轴承正常及故障状态进行识别，结果见表1和表2。由表可知：1)在相同条件下，改进人工蜂群算法的识别率更高，这是由于改进人工蜂群算法通过优化目标函数，显著提高了相似性匹配的精度；2)改进人工蜂群算法所用时间明显较少，表明利用人工蜂群的共享信息机制可以大大缩短故障匹配时间，提高全局寻优能力和故障识别效率。

表1 相似性匹配结果Tab.1 Results of similarity matching

表2 不同算法的对比分析Tab.1 Contrastive analysis of different algorithms

4 结束语

综上所述，改进人工蜂群算法在提高同类型数据匹配精度、减少运算时间方面具有显著效果，在轴承故障诊断过程中可提高故障识别的精度和效率，增强对轴承早期故障的诊断能力，但对于不同轴承而言需要建立不同的无故障模板数据库，还不能够很好的兼容不同类型轴承，对于多轴承状态分析会带来影响。在接下来的研究中，应更侧重于无故障数据模型的建立，使其能适应更多不同类型轴承的故障诊断。