基于拓扑优化和多目标优化的掀背门轻量化研究

郭铃铃，谭东升，刘向征

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

基于拓扑优化和多目标优化的掀背门轻量化研究

郭铃铃，谭东升，刘向征

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

应用拓扑优化和多目标优化设计方法，采用CAE分析软件Altair.OptiStruct和Altair.HyperStudy，对某大型SUV掀背门进行轻量化研究。得到掀背门原始结构的性能参数，确定优化目标；运用Altair.OptiStruct软件对掀背门结构进行拓扑优化，得出掀背门内板筋的最优布置；再运用Altair.HyperStudy软件对掀背门进行多目标优化，包括形状变量和尺寸变量优化，寻找到掀背门内板加强筋的截面尺寸和各部件厚度的最优解。优化后的结构在综合性能提高的同时，总质量也明显减轻，实现了轻量化的目标。

掀背门；拓扑优化；多目标优化；轻量化

0 引言

随着汽车技术的发展，人们对汽车轻量化的要求越来越高。汽车轻量化指的是在保障汽车本身强度、刚度和安全性能的前提下，降低质量，从而提高汽车的动力性，减少环境污染，降低燃料消耗。当下，汽车轻量化技术的主要实施途径包括：轻质材料的使用、新工艺的运用、汽车结构的优化。目前，汽车结构优化是应用最广泛、技术最成熟、效果最明显的途径。文中从汽车结构优化入手，结合CAE技术，综合考虑NVH、刚度、质量等多方面影响，应用拓扑优化和多目标优化等分析方法，对某大型SUV的掀背门结构进行轻量化研究，最后在提升综合性能的前提下达到了明显减重的效果，为后续车型的轻量化设计提供指导。

1 某大型SUV掀背门性能分析

1.1 掀背门刚度和模态仿真分析结果

某车型的掀背门刚度、模态分析结果见表1。

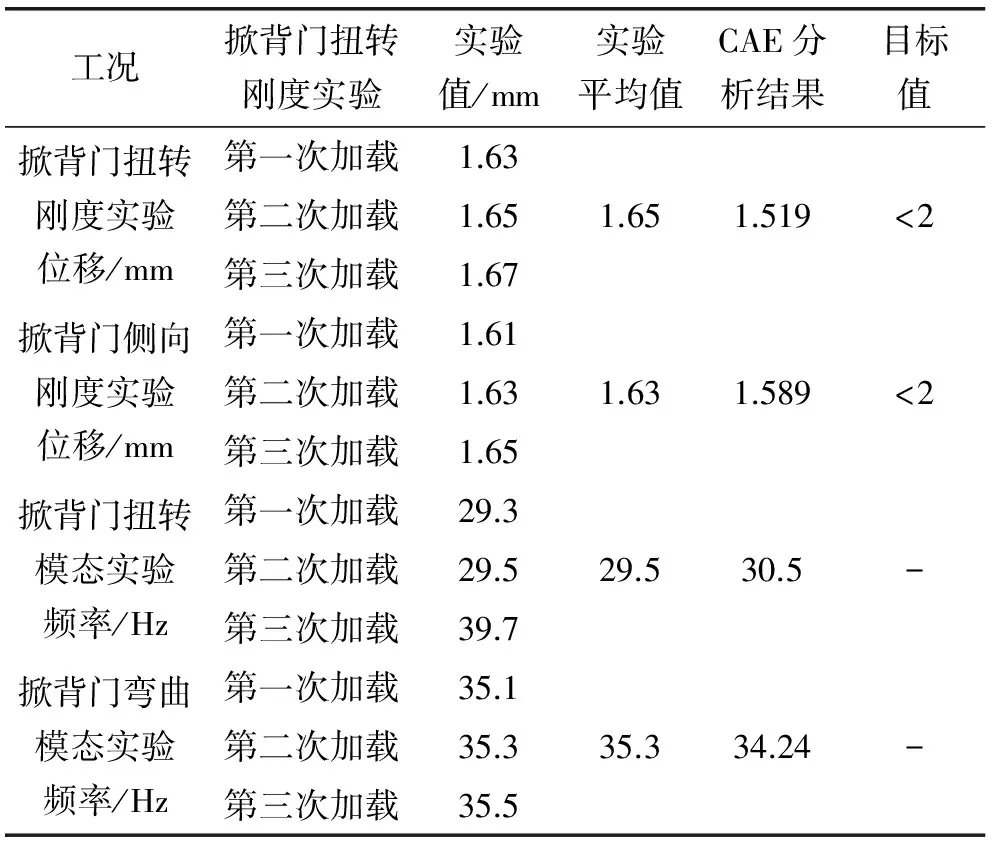
表1 掀背门刚度模态实验值与仿真值结果对比

1.2 掀背门刚度和模态实验验证结果

某车型的掀背门刚度、模态实验结果见表1，实验过程中需加载3次，得出3组数据，最后取平均值。扭转刚度实验状态如图1所示。

图1 掀背门扭转刚度实验

由表1中仿真值与实验值的对比可知：该车型的掀背门扭转刚度、侧向刚度、扭转模态、弯曲模态仿真分析结果与实验结果基本保持一致，说明文中建立的有限元模型具有一定的精度，能够满足后续轻量化优化分析的需要。同时，各性能均有较大富余量，可通过以下结构优化，在保证性能的同时达到减重的效果。

2 掀背门拓扑优化

2.1 拓扑优化基本理论和方法

2.1.1 拓扑优化基本理论

拓扑优化是指在指定的设计区域内，寻找最佳的材料分布。

一个优化问题通常由以下3个要素组成：

(1)设计变量是发生改变从而影响目标函数的变量；

(2)目标函数是要求最优的设计性能，实现对系统响应的最大(小)化，或者使响应趋于目标值，是关于设计变量的函数；

(3)约束条件是对设计的限制，是对设计变量和其他性能的要求。

拓扑优化数学模型为：

Minimize：f(X)=f(x1,x2,…,xn)

Subjectto:g(X)≤0j=1,…,m

hk(X)≤0k=1,…,mh

其中：X=(x1,x2,…,xn)是设计变量，如产品的结构尺寸等；f(X)是设计目标，如各种力学性能或者质量；g(X)和h(X)是需要进行约束的设计响应，如对产品工作时的变形和应力水平进行约束[1]。

2.1.2 拓扑优化方法

常用的结构拓扑优化方法包括：均匀化法和变密度法[1]。均匀化法由于理论比较复杂，变量繁多，目前主要应用在理论研究领域。变密度法以人为假定的单元密度(伪密度)为设计变量，单元密度在0～1之间连续取值，优化求解后单元密度为1(或靠近1)表示该单元位置处的材料很重要，需要保留；单元密度为0(或靠近0)表示该处的材料不重要，可以去除，从而达到材料的高效率利用，实现轻量化设计[2]。与均匀化法相比，变密度法的设计变量少，计算程序实现起来简单，因此是最常用的拓扑优化方法[2]。

拓扑优化变密度法的数学模型可用下式表示：

Minf(x)

xmin≤xi≤1,i=1,…,n

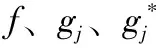
2.2 掀背门拓扑优化过程

结合掀背门以上4种工况，在保证掀背门整体性能的前提下，利用Altair.OptiStruct软件对掀背门内板进行拓扑优化设计。原掀背门结构如图2所示，对原掀背门内板进行拓扑结构优化，实现设计区域内的材料最优分布。

图2 掀背门内板原始模型

(1)定义拓扑优化的设计空间

考虑到整车总布置的空间约束，在不改变掀背门锁、铰链、雨刮电机、气弹簧等安装孔位置、同时不改变密封面的位置的情况下，选择掀背门内板中部作为优化设计区域，如图3所示。

(2)定义拓扑优化的设计变量

设计变量为设计空间里每个单元的密度。考虑到掀背门内板的加工性，制造约束中最小成员尺寸设置为20 mm，并且选择对称约束。

(3)定义拓扑优化的目标

在保证NVH和刚度性能的同时，使掀背门内板的使用材料最少。

(4)定义拓扑优化的设计约束

选择以上掀背门扭转刚度、侧向刚度、扭转模态和弯曲模态4种工况，作为掀背门内板拓扑优化的约束工况。

图3 掀背门内板拓扑优化区域

(5)掀背门拓扑优化结果

掀背门内板拓扑优化结果如图4所示，根据工程经验和产品的可加工性，对掀背门内板拓扑优化的结果进行工程解析，得到可行性设计的掀背门内板结构，如图5所示。拓扑优化结果见表2。

图4 掀背门内板拓扑优化结果

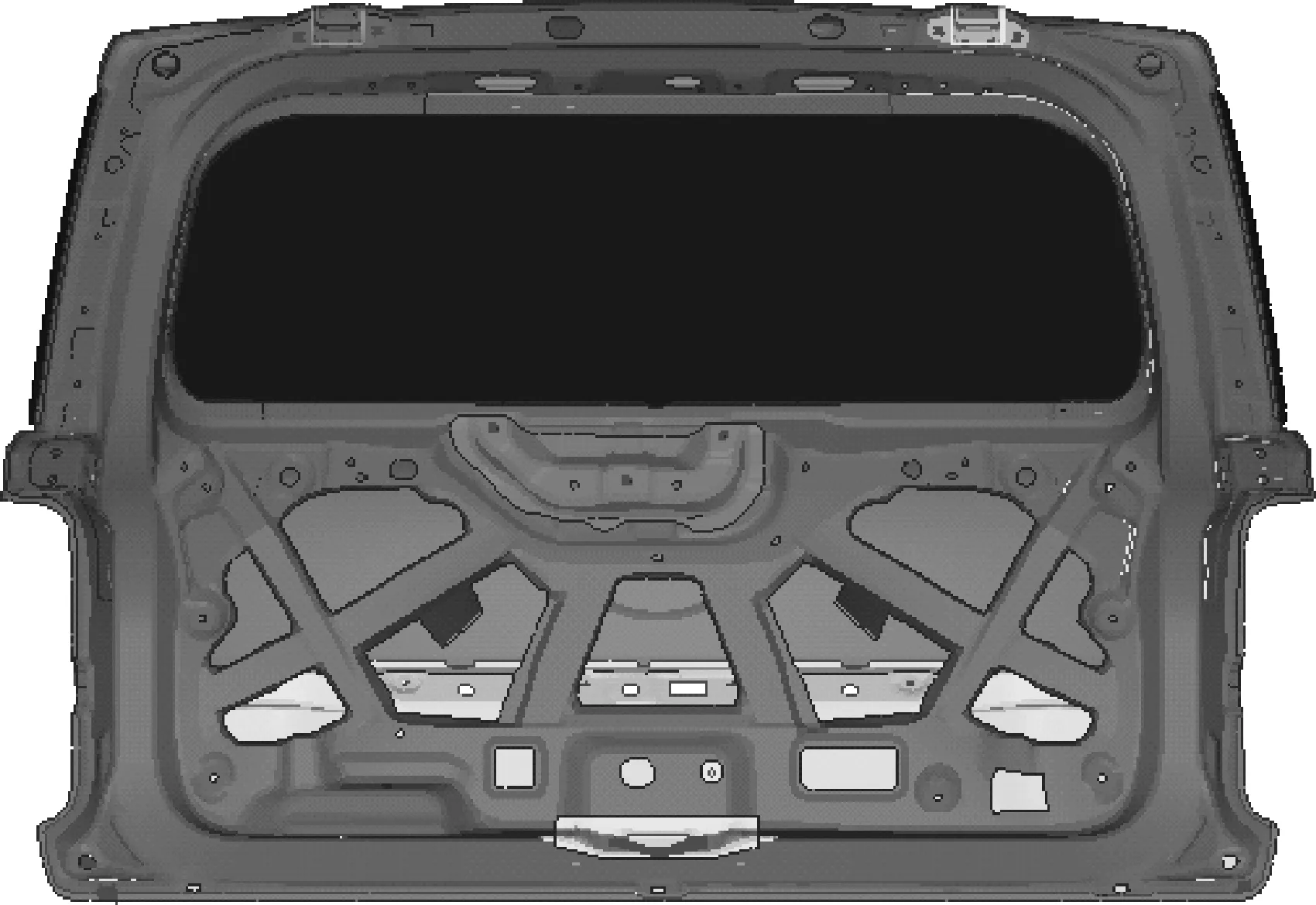
图5 掀背门优化模型

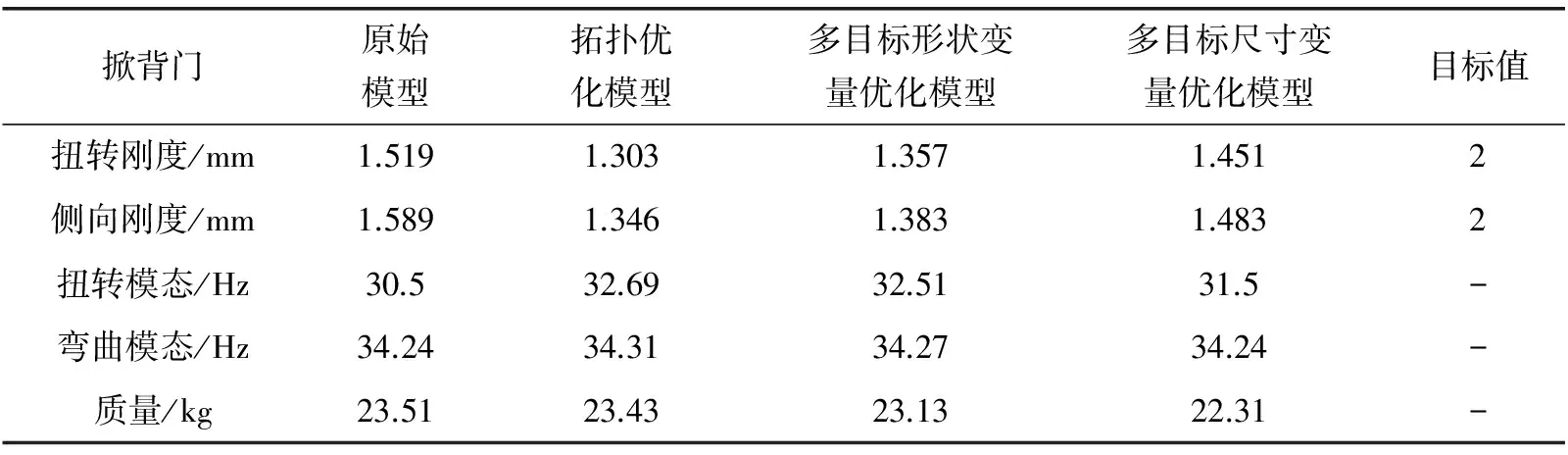
掀背门原始模型拓扑优化模型多目标形状变量优化模型多目标尺寸变量优化模型目标值扭转刚度/mm1．5191．3031．3571．4512侧向刚度/mm1．5891．3461．3831．4832扭转模态/Hz30．532．6932．5131．5-弯曲模态/Hz34．2434．3134．2734．24-质量/kg23．5123．4323．1322．31-

由拓扑优化的结果可知：拓扑优化后的结构使综合性能均有较大提升。但由于拓扑优化只能得出掀背门内板筋的最优布置位置，无法确定各个筋的具体最优截面尺寸，故需要在此基础上，通过以下的多目标形状变量优化来确定掀背门内板筋的长、宽、高的最优尺寸。

3 掀背门多目标优化

3.1 多目标优化理论

目标优化问题一般指的是通过一定的优化算法获得目标函数的最优解。当优化问题中的目标函数为一个的时候，称为单目标优化(Single-objective Optimization Problem, SOP)，当优化的目标函数为两个或者两个以上的时候，则称为多目标优化(Multi-objective Optimization Problem, MOP)。单目标优化问题的解为有限解，而多目标优化问题中的目标之间是相互矛盾的，优化解通常是一组均衡解。多目标优化是一种针对于涵盖了多学科、多领域的复杂系统进行优化设计的方法，强调的是各学科、各子系统在单独优化设计的基础上，相互之间的并行协作。

多目标优化问题的数学描述由设计变量、目标函数、约束函数组成。

一般多目标优化数学描述如下：

Min(& Max)y=f(x)=[f1(x),f2(x),…,fn(x)](n=1,2,…,N)

S.t.g(x)=[gz(x),g2(x),…,gk(x)]≤0

h(x)=[hz(x),h2(x),…,hm(x)]≤0

x=[x1,x2,…,xd,…,xD]

xdmin≤xd≤xdmax(d=1,2,…,D)

其中：x为D维决策变量，y为目标函数，N为优化目标总数；fn(x)为第n个子目标函数；g(x)为k项不等式约束条件，h(x)为m项等式约束条件，约束条件构成了可行域；xdmin和xdmax为向量搜索的上下限。

文中采用全局响应面法GRSM(Global Response Surface Method)对掀背门进行多目标优化。

全局响应面法(GRSM)是一种基于响应面的直接优化方法，与其他直接优化方法相比，具有实用、高效的优点。该算法从初始值周围一些随机的设计点开始优化，在每一个迭代步中，基于响应面的优化会产生一些新的设计点，从而在兼顾局部搜索和全局搜索之间取得一个较好的平衡[3]。所有这些在迭代步中产生的设计点以并行的方式进行求解，新产生的设计点将用来更新响应面以更好地对实际模型进行拟合[3]。全局响应面法具有全局搜索能力，可进行单目标优化或多目标优化，可设置约束条件，也可以进行无约束的优化[3]。

3.2 多目标形状变量优化

首先通过有限元前处理软件Altair.HyperMesh中的网格变形模块HyperMorph[4]对掀背门内板网格进行变形处理，再利用Altair.HyperStudy软件对掀背门内板基于全局响应面法进行多目标形状变量优化分析，该优化模型的形状优化设计变量包括掀背门内板筋的宽度和高度方向上的6个形状变量。

3.2.1 模型参数化

将掀背门内板筋的形状尺寸作为优化分析的设计变量，HyperMesh中的网格变形模块HyperMorph是用于创建形状变量的专门工具，在HyperMorph中可以对网格形状进行任意调整来得到新的网格位置，原始网格位置和变形后得到的新的网格位移之间各个节点自由度的矢量就称为形状变量。在HyperMorph中可以创建任意多个形状变量，这些变量在优化过程中根据优化算法得到的变形系数进行独立变化。由原始形状与形状变量的矢量和可以得到新的网格形状，即新设计。在HyperMesh的网格变形模块HyperMorph中创建的形状变量可直接与HyperStudy建立连接并传递，HyperStudy会根据优化过程得到的系数不断调用HyperMesh来更新网格，再提交给求解器计算。

如图6—11所示：创建了形状变量1～形状变量6，分别为掀背门内板筋的宽度和高度。

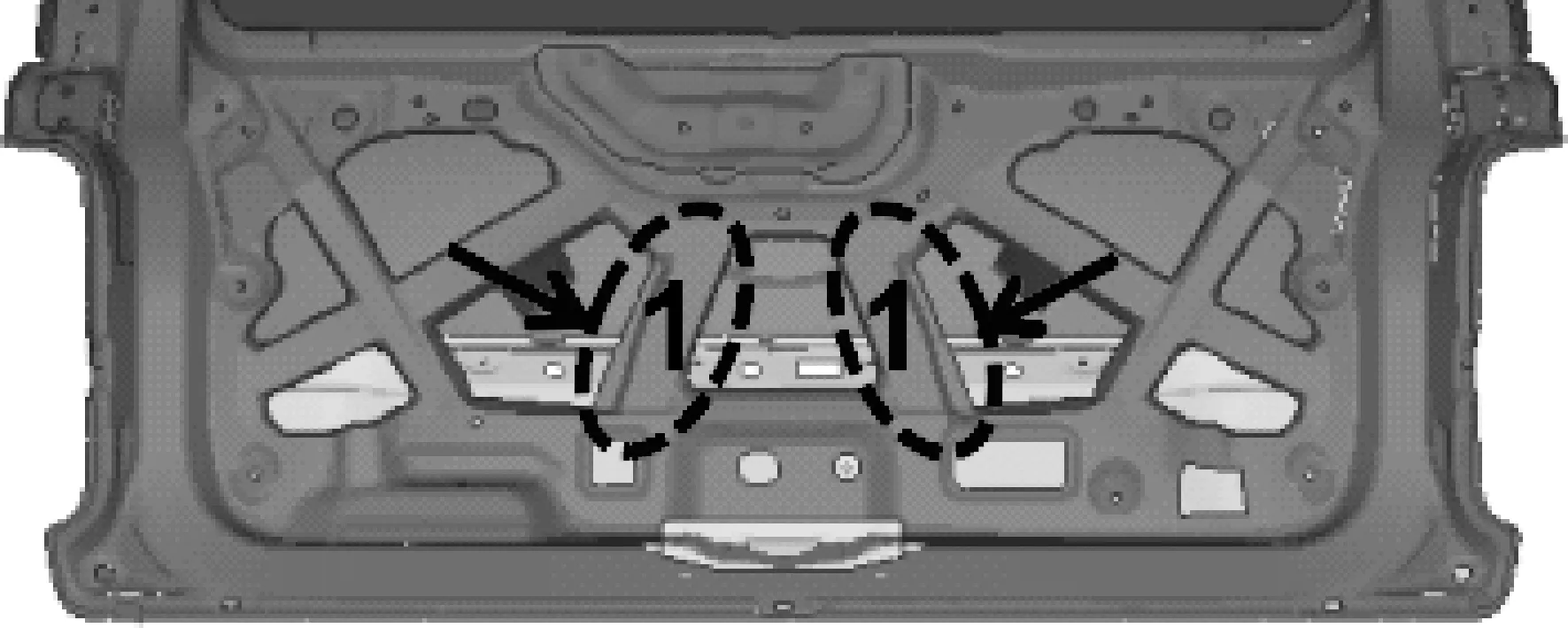
图6 形状变量1

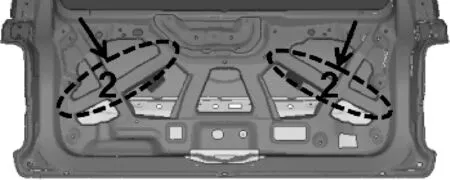
图7 形状变量2

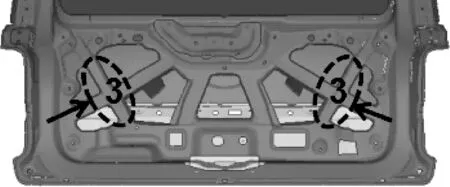
图8 形状变量3

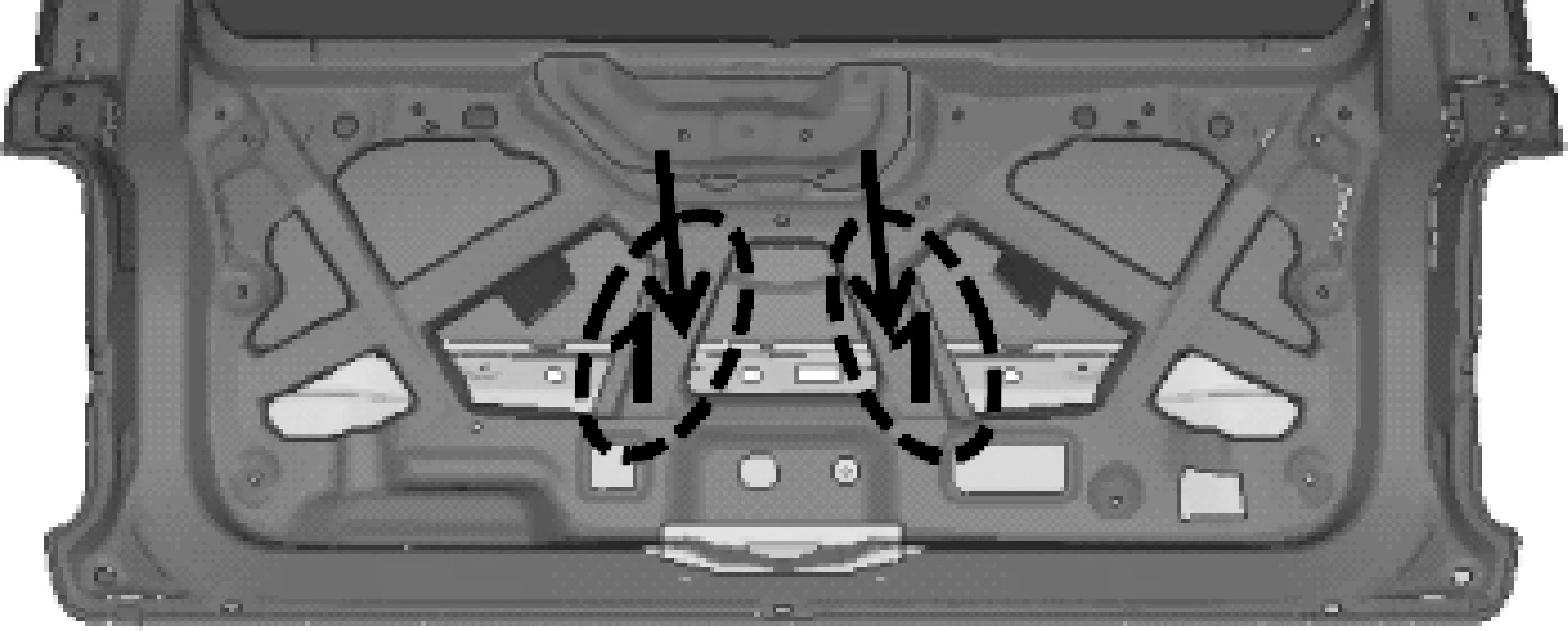
图9 形状变量4

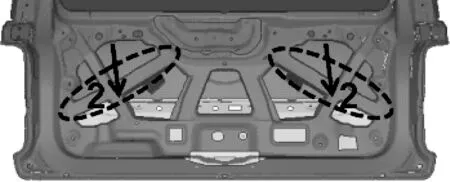
图10 形状变量5

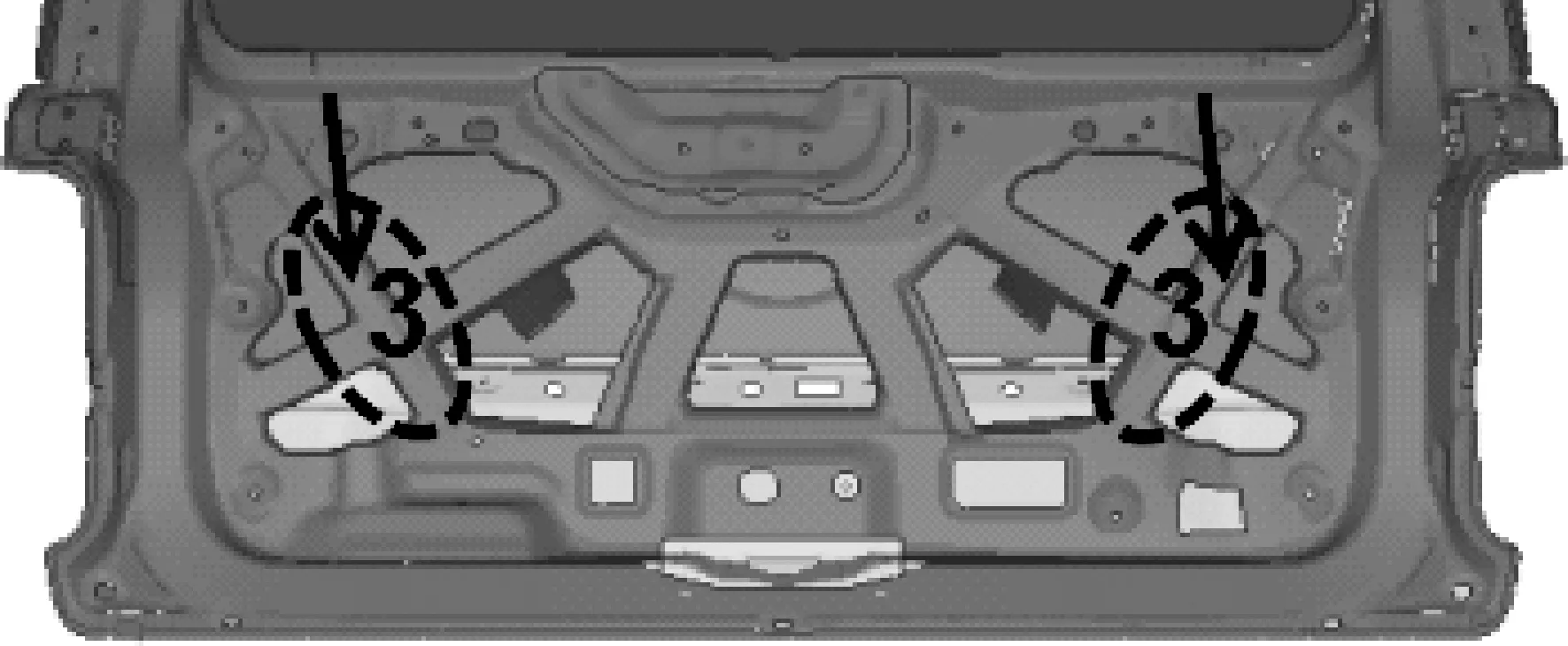
图11 形状变量6

3.2.2 优化模型建立及优化结果

以掀背门体积最小化，一阶弯曲、扭转模态频率最大化作为优化目标，最大变形量作为约束，用全局响应面法(GRSM)进行多目标优化。

优化后，掀背门内板筋的宽度和高度选用迭代后的最优解，最终优化结果如下：

形状变量1，即掀背门内板筋1的宽度为35 mm；

形状变量2，即掀背门内板筋2的宽度为25 mm；

形状变量3，即掀背门内板筋3的宽度为25 mm；

形状变量4，即掀背门内板筋1的高度为10 mm；

形状变量5，即掀背门内板筋2的高度为10 mm；

形状变量6，即掀背门内板筋3的高度为10 mm。

优化模型如图12所示，多目标形状变量优化结果见表2。

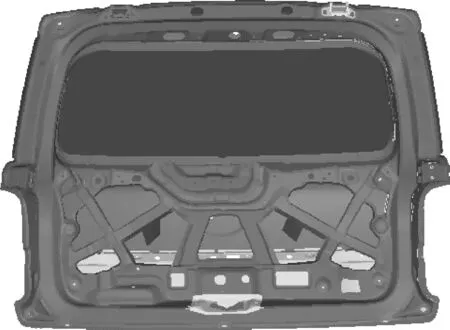
图12 多目标(形状变量)优化分析结果

3.3 掀背门多目标尺寸变量优化

3.3.1 模型参数化

利用Altair.HyperStudy软件进行多目标尺寸变量优化，选取对掀背门性能和质量影响较大的11个部件的厚度作为多目标尺寸变量优化的设计变量，见图13，设计变量参数设置见表3。

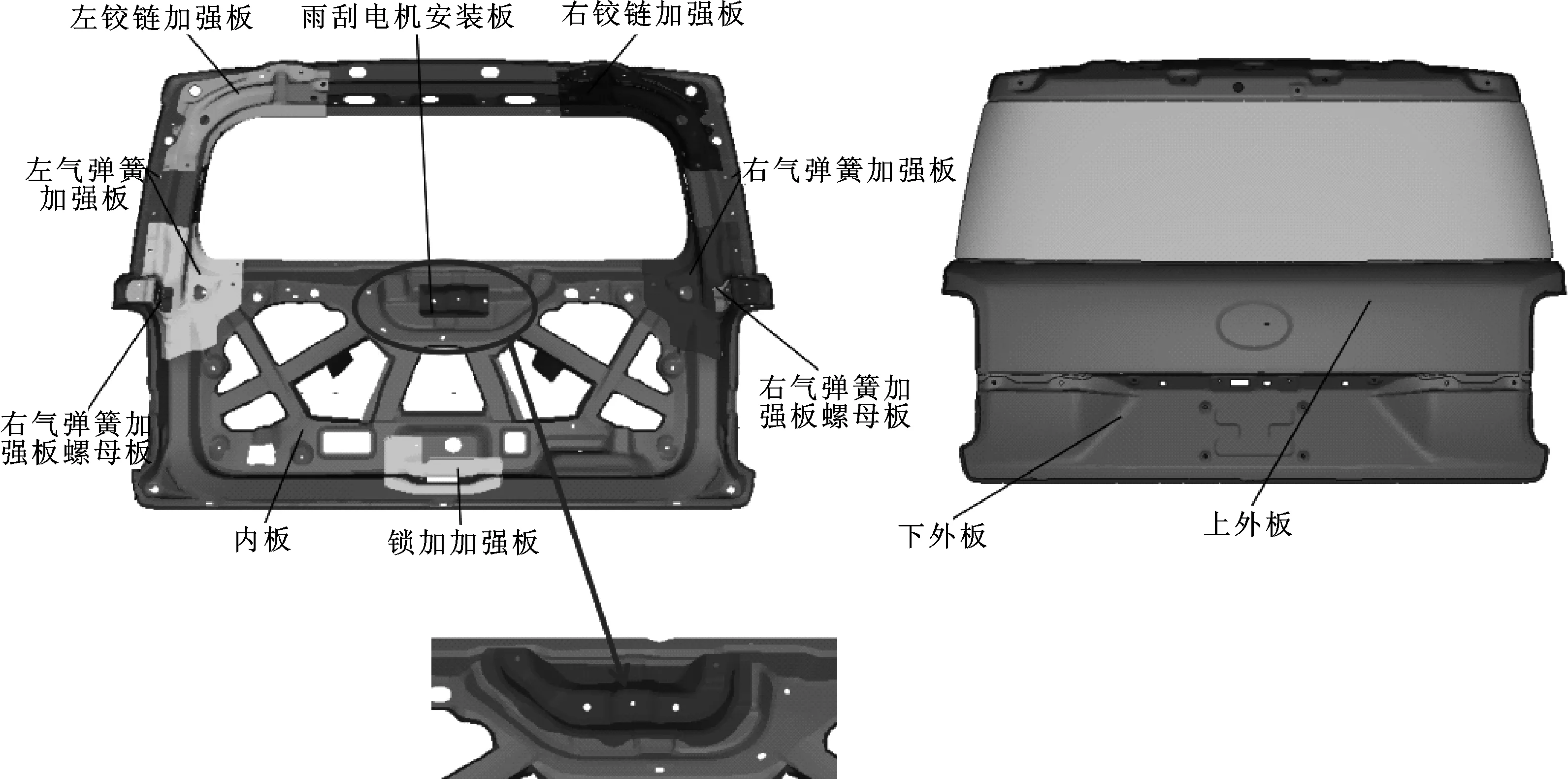
图13 掀背门模型

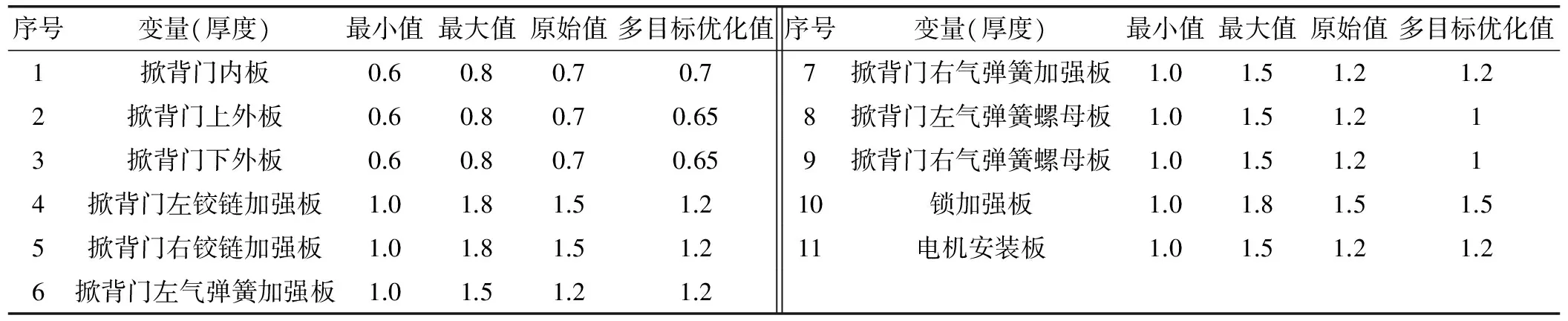
表3 多目标(尺寸变量)优化参数设置 mm

3.3.2 优化模型建立

多目标尺寸变量优化的目标是使掀背门质量最小的同时掀背门各工况性能满足目标要求，因此该多目标优化问题可被定义为：

Obj：min[m] max[F1] max[F2]

Ri≤αi,Fj≥βji=j=1,2

其中：m表示掀背门总成质量(kg);F1表示掀背门一阶扭转模态;F2表示掀背门一阶弯曲模态;Ri表示扭转刚度和侧向刚度工况下的变形量(mm);Fj表示掀背门一阶扭转和一阶弯曲模态(Hz)；αi和βj分别代表各相应工况下的目标值[1]。即分别以扭转刚度工况和侧向刚度工况的目标变形量为约束条件，以扭转模态和弯曲模态工况的目标频率最大化，以车门质量最轻为优化目标，经过50次迭代，约束函数与目标函数均收敛，选取各响应的收敛值为此次优化的最优解。取整后，优化前后设计变量厚度的变化如表3所示。

3.3.3 优化结果

将多目标优化(尺寸变量)的优化结果代入有限元模型进行计算，多目标尺寸变量优化结果如表2所示。

通过以上拓扑优化和多目标优化，在保证各项性能均有提升的前提下，达到了明显减重的效果，最终减质量1.2 kg，使得掀背门总成减重5.1%。

4 结论

以某大型SUV掀背门为设计对象，采用了拓扑优化和多目标优化技术相结合的优化设计方法，利用当今通用的CAE技术和工具，找到了掀背门内板加强筋的最优布置和截面形状，对掀背门各部件的厚度进行了优化。通过以上优化方法，优化后的掀背门综合性能提高的同时，总质量也明显减轻，实现了轻量化的目标。

分析中涉及的优化方法对于汽车中其他零部件的正向开发设计具有一定的参考意义，可针对具体的优化分析项，选用适合的设计变量、约束条件和目标函数，能使优化过程更加事半功倍。将此轻量化方法应用到项目前期开发和设计中，可大大缩短项目的开发周期，降低产品成本，提高产品的综合性能。

【1】洪清泉，赵康，张攀.OptiStruct & HyperStudy理论基础与工程应用[M].北京:机械工业出版社，2012.

【2】季学荣，丁晓红.基于拓扑和形貌优化的汽车发动机罩板设计[J].机械设计与研究,2011,27(1):35-38. JI X R,DING X H.Design Optimization of Engine Hood Based on Topology and Topography Optimization[J].Machine Design & Research,2011,27(1):35-38.

【3】尹安东，曹诚，徐俊波，等.基于全局响应面法的电动汽车车架多目标优化[J].汽车科技,2014(5)：8-11. YIN A D,CAO C,XU J B,et al.Multi-objective Optimization of Electric Vehicle Frame Based on GRSM[J].Automobile Science & Technology,2014(5)：8-11.

【4】王钮栋，金磊，洪清泉.HyperMesh & HyperView应用技巧与高级实例[M].北京:机械工业出版社，2012.

【5】杨佳璘，赵桂范，顾海明，等.轿车发动机罩拓扑结构优化及其轻量化设计[J].机械设计与制造,2013(5):32-35. YANG J L,ZHAO G F,GU H M,et al.Topological Structure Optimization and Lightweight Design of the Car Engine Hood[J].Machinery Design & Manufacture,2013(5):32-35.

【6】刘孟祥，胡辽平，谢辉.基于形状变量和全局响应面法的增压器涡轮多目标优化[J].内燃机工程,2013,34(4):71-76. LIU M X,HU L P,XIE H.Multi-objective Optimization of Turbocharger Turbine Based on Shape Variable and Global Response Surface Method[J].Chinese Internal Combustion Engine Engineering,2013,34(4):71-76.

【7】黄永旺，袁登木.多目标拓扑优化技术在汽车行业中的应用[C]//第五届中国CAE工程分析技术年会论文集,2011:117-119.

【8】谢晖，李全.铝合金材料发动机罩内罩板优化设计研究[J].机械工程与自动化,2015(2):42-44. XIE H,LI Q.Hood Inner Cover’s Optimized Design Based on Aluminum Alloy[J].Mechanical Engineering & Automation,2015(2):42-44.

Research on Light Weight of Lift Gate Based on Topology Optimization and Multi-objective Optimization

GUO Lingling，TAN Dongsheng，LIU Xiangzheng

(GAC Automotive Engineering Institute, Guangzhou Automobile Group Co.,Ltd., Guangzhou Guangdong 511434,China)

With the application of topology optimization and multi-objective optimization based on CAE analysis softwares Altair.OptiStruct and Altair.HyperStudy, the lightweight research on a large SUV lift gate was made. The performance parameters of the original structure of the lift gate were gotten to determine the optimal goal. Then topology optimization to the structure of the lift gate was completed by using Altair.OptiStruct software, the optimal layout of the lift gate door panel reinforcement was gotten. Multi-objective optimization to the lift gate was completed by using Altair.HyperStudy software, including the shape optimization and the size variable optimization. The optimal values of the section sizes of the lift gate door panel reinforcement and the thicknesses of the various components were found. Not only the optimized structure has improved comprehensive performance, but also the total quality is reduced. The goal of lightweight is achieved.

Lift gate; Topology optimization; Multi-objective optimization; Lightweight

2017-02-22

郭铃铃(1989—)，女，工学学士，工程师，研究方向为汽车车身强度刚度分析。E-mail:guolingling@gaei.cn。

10.19466/j.cnki.1674-1986.2017.06.002

U463.83+4

A

1674-1986(2017)06-005-06