两种滑行试验处理方法对比及风速对滑行距离影响的研究

孙涛，王振来

(中国第一汽车股份有限公司技术中心，吉林长春 130011)

两种滑行试验处理方法对比及风速对滑行距离影响的研究

孙涛，王振来

(中国第一汽车股份有限公司技术中心，吉林长春 130011)

对比了两种滑行试验数据处理方法，比较两种方法计算结果的差异，并且研究了滑行阻力系数中常数项、一次项、二次项的影响因素，提出一次项系数不能省略的依据，最后分析了纵向风速对滑行试验距离的影响程度。

滑行阻力；滑行阻力系数；滑行试验数据处理方法

0 引言

在整车研发过程中，计算仿真、整车转鼓试验、汽车底盘状态检查、产品定型试验等都需要滑行试验数据作为输入，所以能否获得准确的滑行试验结果至关重要。滑行(Coasting)是指汽车在水平路面且无风的条件下加速至某预定车速后，摘挡脱开发动机，利用汽车的动能继续行驶的减速运动[1]。

结合滑行的定义以及汽车动力性理论的相关内容可以知道，车辆在滑行时没有坡度阻力，它在滑行状态时的行驶方程为：

(1)

式中：Ff为滚动阻力；Fw为空气阻力；m为车辆质量，单位为kg；v为车速，单位为m/s;δc为排除发动机飞轮转动惯量后的汽车旋转质量换算系数，δc=∑Iw，Iw为轮胎的转动惯量；Tr为滑行时传动系施加于驱动轮的摩擦阻力矩与从动轮摩擦阻力矩之和，相关文献认为Tr可以不计，但文中的研究结论认为Tr是必须要考虑的项目。

关系式(1)只是从理论上分析了滑行试验的力学规律，但并不适用于实际道路滑行试验的数据处理。目前对滑行数据进行处理的目的是得到车辆滑行状态时车速与车辆阻力(或者阻功率)的关系式，一般认为汽车滑行阻力与其行驶车速呈现一个二次函数的关系，即：

F=K0+K1v′+K2v′2

(2)

式中：v′为车速，其单位为km/h;F为汽车在滑行时受到的总阻力。将式(2)改写为微分方程形式，并转换单位到国际基本单位：

(3)

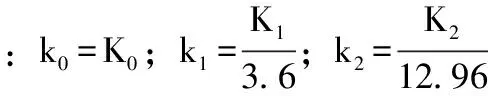
1 两种滑行试验数据处理方法

实际道路阻力滑行试验的结果输出为滑行阻力系数K0、K1、K2，主要应用于底盘测功机的阻力模拟、车辆检查以及与竞品对比分析。目前大多采用GB18352.3-2005《轻型汽车污染物排放限值及测量方法(中国Ⅲ、Ⅳ阶段)》附录CC给出的方法求出滑行阻力后，再利用最小二乘法拟合出滑行阻力系数，该方法以下称为标准法。因标准法取固定的点(速度，时间)描述整个试验过程,故该方法直观简单易操作。另一种方法是从微分方程(3)入手，通过求解该微分方程，得到速度与时间的关系式，而滑行试验的直接结果就是速度、时间和距离，这就变成了已知速度、时间，求解滑行阻力系数的问题。可以利用MATLAB软件Toolbox中的曲线拟合工具，得到基于最小二乘法的滑行阻力系数，该方法以下称为方程法。方程法略去了对滑行数据的求阻力处理过程，直接利用原始数据进行拟合。需要特别提出的是，文中并没有对行驶阻力进行标准环境(20 ℃，100kPa)下的校准，但数据仍然具有对比性。

1.1 省略滑行末段数据

图1是某车型滑行试验的速度-时间曲线，可以发现曲线末尾阶段(约1km/h至0)并不符合试验数据预期。这是由试验测试仪器精度、润滑状态的改变等因素造成：此试验采用的车速传感器精度为0.1km/h，在速度接近为0时会有误差；传动系用的润滑油在低转速下润滑效果变差，也可能增加阻力；另外，滑行速度过小的情况下滚动阻力与风阻的比例关系差距悬殊，此时测量的滚动阻力系数误差较大[2]，会影响试验数据处理精度。基于以上原因，阻力计算中略去末尾阶段的滑行数据。

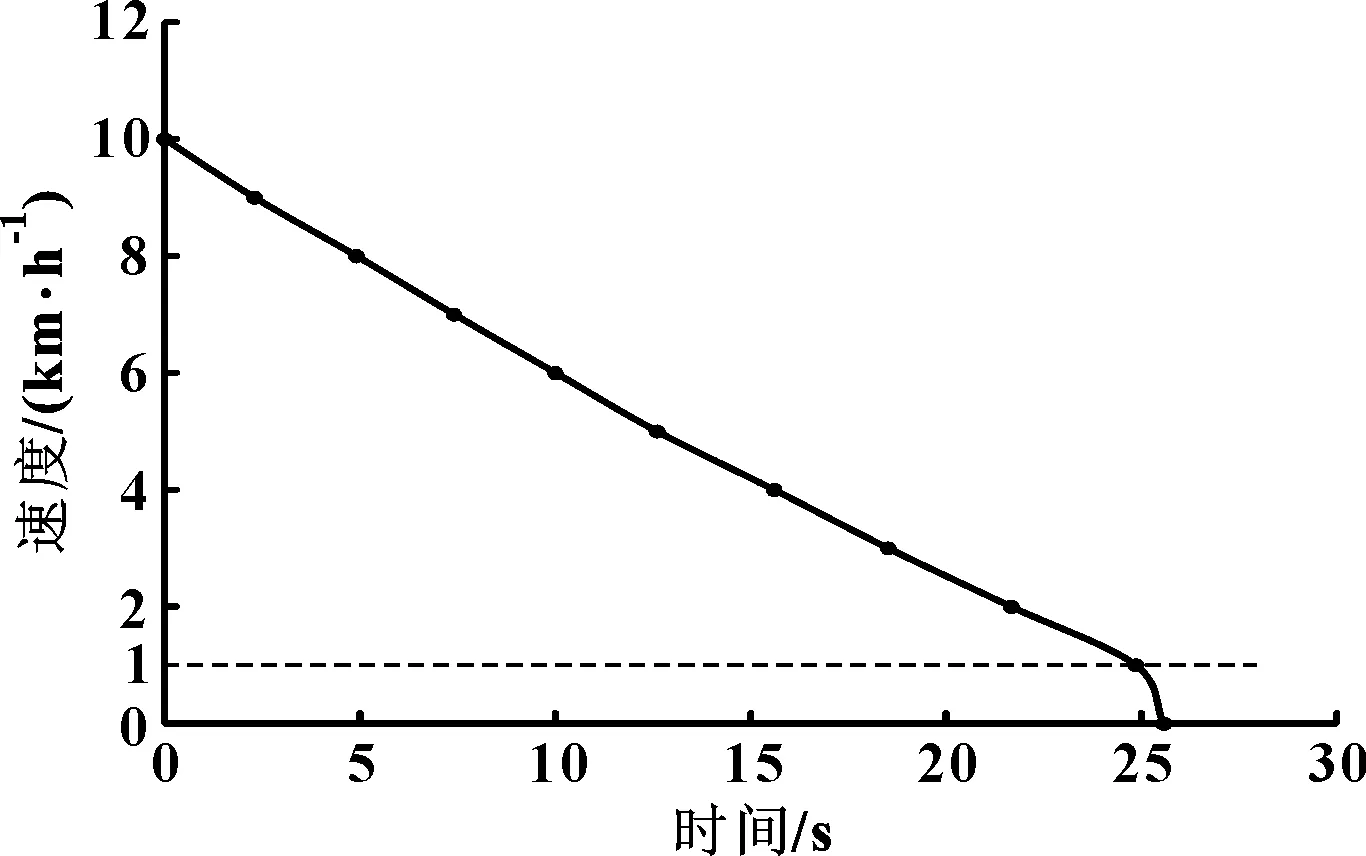
图1 某车型滑行试验速度-时间曲线

1.2 标准法

标准法假设在滑行试验过程中的某一速度区间内车辆做匀减速滑行，即假设速度在(v+5)～(v-5) km/h区间内的减速度是一致的，那么就可以利用公式(4)计算得到在速度v时的阻力:

(4)

式中：Δv为滑行车速变化幅度，其值为2.78 m/s；Δt为车辆由速度(v+5) km/h滑行到(v-5) km/h所经过的时间。得到指定车速的滑行阻力之后，用最小二乘法拟合出公式(2)，就得到了滑行阻力系数的值。

1.3 方程法

方程法没有假设条件，不对原始数据进行处理，而是利用解微分方程(3)之后得到的带滑行阻力系数的时间-速度关系式T=f(v)直接拟合滑行试验得到时间-速度曲线。其中：微分方程的初始条件为在时间T=0时，v=34.72 m/s(125 km/h)；T=t时，v=2.78 m/s(10 km/h)解微分方程得到时间-速度关系式(5)：

(5)

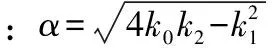
表1列出了某两个车型分别用标准法和方程法得到的滑行阻力系数值。车型Ⅰ为某轿车车型，车型Ⅱ为某SUV车型。两车型的试验环境风速均为0，其余试验条件均满足GB/T 12534-1990《汽车道路试验方法通则》的要求。

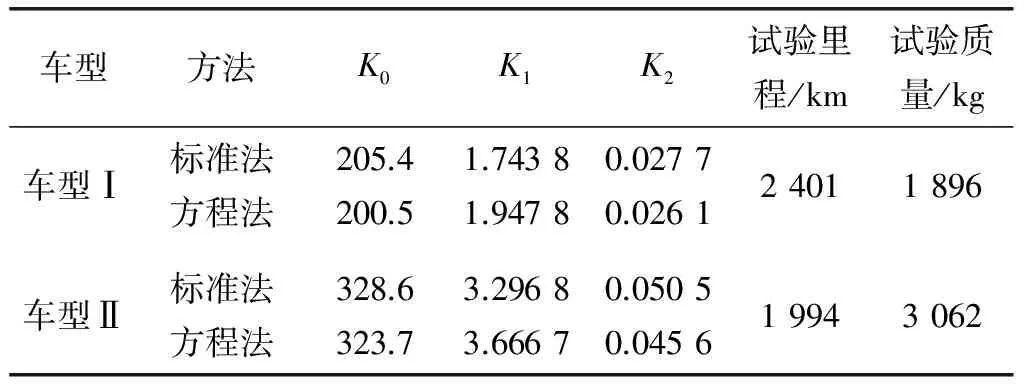
表1 滑行阻力系数拟合值

通过表1的滑行阻力系数去计算相应车速的滑行阻力，得到图2和图3。

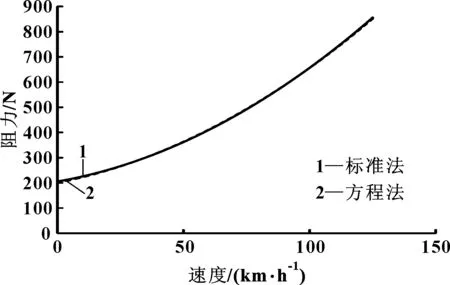
图2 车型Ⅰ的滑行阻力曲线

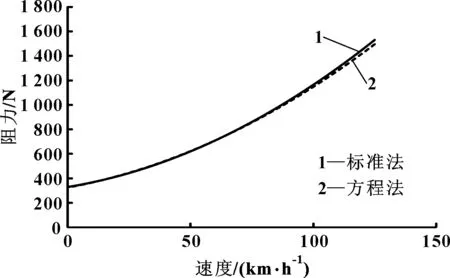
图3 车型Ⅱ的滑行阻力曲线

可以发现，用这两种方法得到的两个车型的滑行阻力系数非常接近，在较高滑行车速段利用方程法得到的实际滑行阻力会稍小于用标准法得到的滑行阻力，见表2。但在实际的试验车速范围内，基本可以将两条曲线看作是重合的。

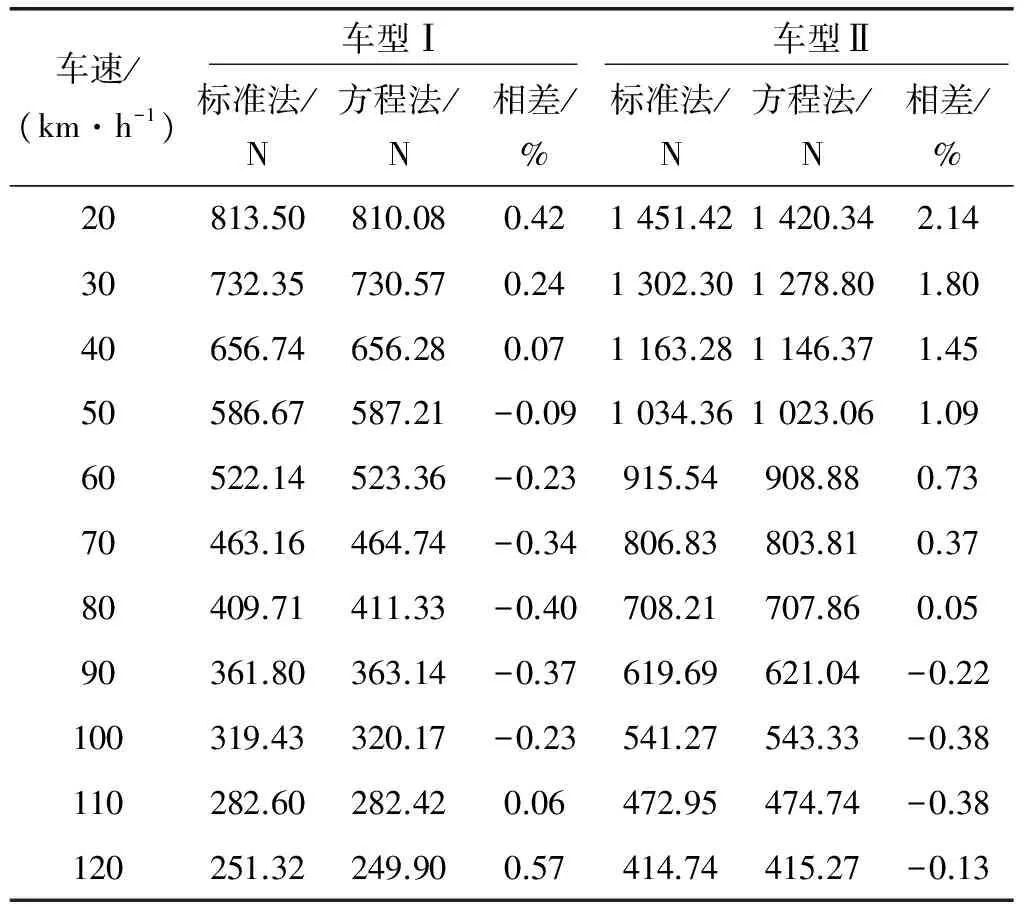
表2 各车速下计算滑行阻力对比

2 滑行阻力系数的一次项

基于滚动阻力系数为常数项、忽略传动系阻力以方便数据对比的假设，有人将道路滑行阻力系数中的一次项系数省略。比如SAEJ1263-FEB96标准《道路载荷测量和用滑行技术进行测功机模拟》中，将滑行的滑行微分方程(3)更改为：

(6)

可以看出，该微分方程省略了一次项系数，根据微分方程(6)解出的时间-速度关系式为：

t=δc×m×ε×(arctana-arctanb)

(7)

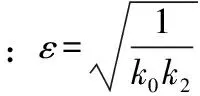
这样，方程(3)和方程(6)就用两种不同的曲线描述了同一个滑行试验。通过曲线可以比较一下省略一次项系数和不省略一次项系数的滑行阻力曲线的不同。表3给出了两个车型在省略一次项后用方程法得出的道路阻力滑行系数，图4、图5给出了两个车型采用不同表达方程所描述的曲线。可以发现：省略了一次项系数的曲线，在40～90 km/h范围内的阻力值较低，其余速度区间阻力值较高。

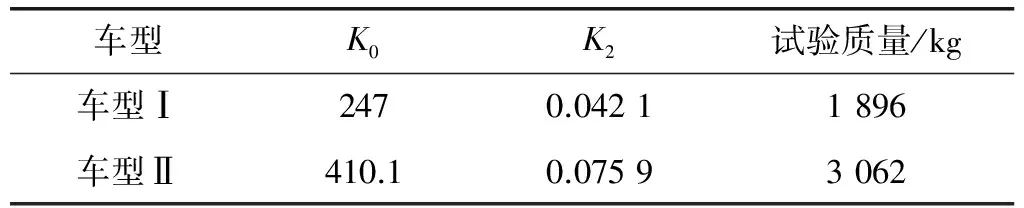
表3 省略一次项系数后计算滑行阻力系数

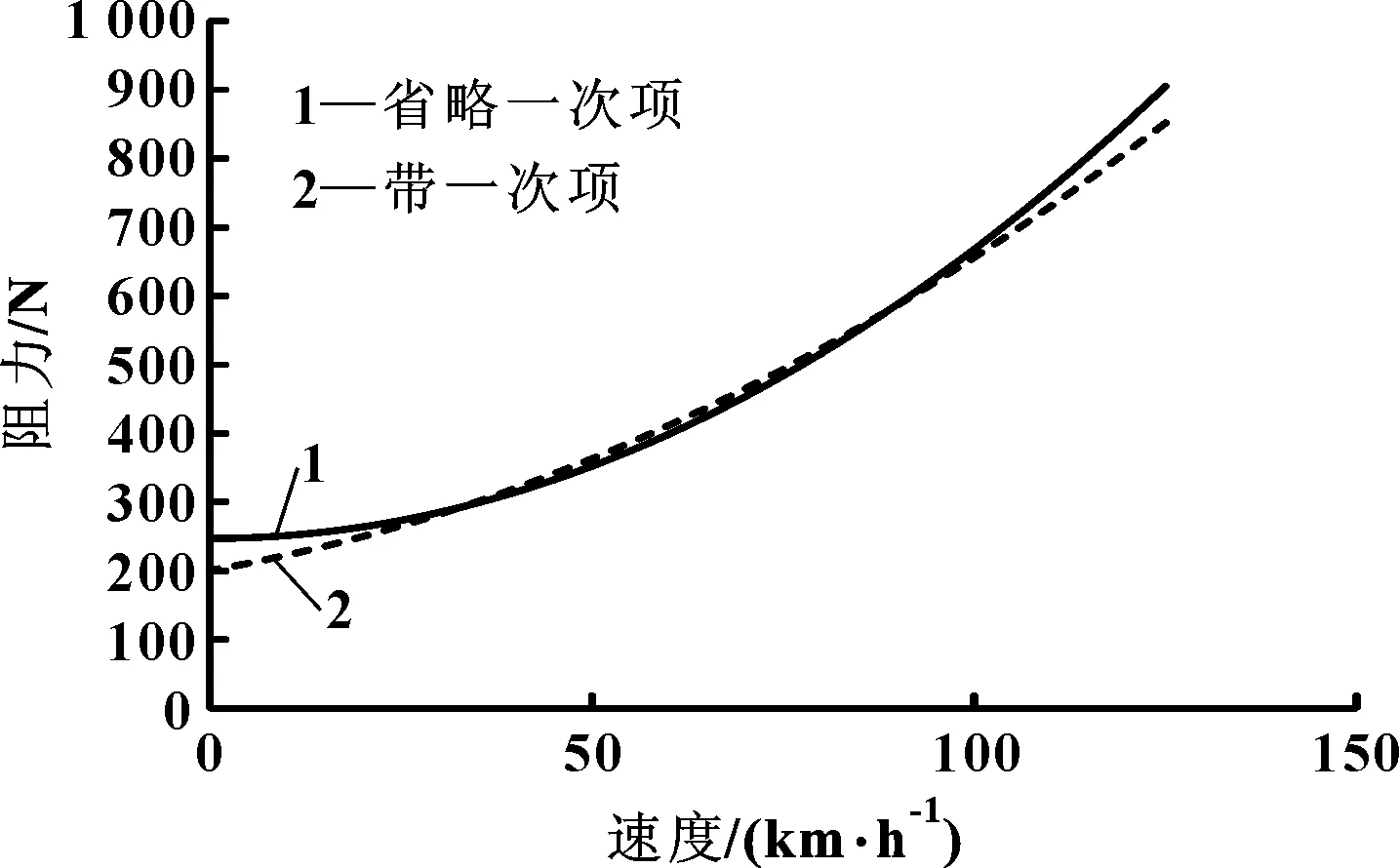
图4 车型Ⅰ两种阻力表达方式曲线

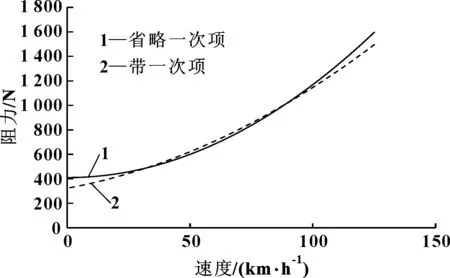
图5 车型Ⅱ两种阻力表达方式曲线

表4给出了车型Ⅰ在低速时的阻力分布情况。

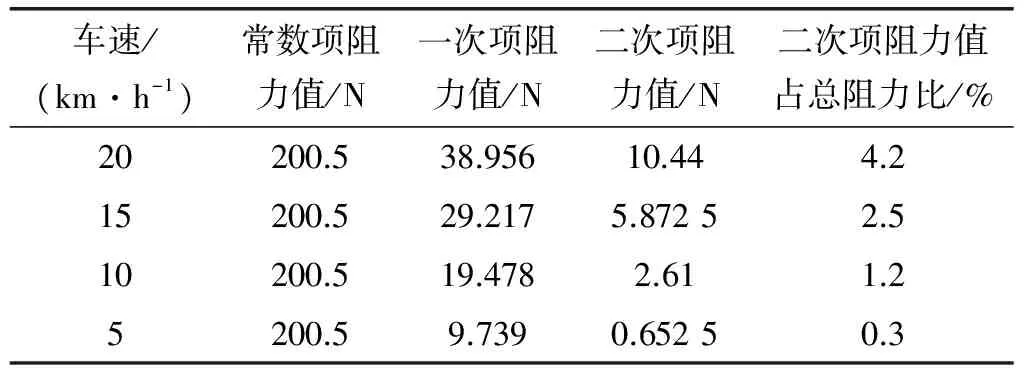
表4 车型Ⅰ在低速状态下的阻力分布

此表数据显示:车速在20 km/h下，二次项阻力占总阻力的比值不到5%。此时可以认为，滑行阻力在低速下(20 km/h以下)的表示为[3]：

初始条件为v=5.556 m/s(20 km/h)时，t=0，解方程得：

代入车型Ⅰ的滑行数据得k0=208.1，k1=1.934 1。这与用方程法计算出的滑行阻力系数基本一致，也就说明利用方程法计算出的滑行阻力一次项系数的确是滚动阻力和传动系阻力受车速影响的综合体现。进一步说，含有一次项的汽车滑行阻力方程中，二次项系数只与车辆的风阻系数以及迎风面积有关，那么在已知车辆迎风面积的情况下，就可以计算出车辆的风阻系数。

依据省略一次项的阻力-速度曲线可以用于简单的对比分析的假设，省略一次项的表达是没有问题的，但是无论从数据还是从曲线来看，这种对比是“失真”的：低速段和高速段的阻力过大，中速段的阻力较小，这种曲线描述仅仅是数学概念上的拟合，不符合实际。

由此可以说，省略了一次项系数之后再去对比车辆滚动阻力以及风阻是不合适的。传动系阻力特别大而风阻相对小的车辆在省略一次项系数后的行驶阻力表达式中体现出较大的滚动阻力或者风阻，这会影响车辆试验结果的对比。在产品开发中，对标车的道路滑行试验就不应该省略一次项系数，以保证对比的车辆在各个方面的差异性足够正确且明显。另外，如果存在变速器、主减速器的润滑油加注过多的情况，此时搅油造成的阻力也会体现在一次项阻力系数上。

3 风速对滑行距离的影响

在滑行阻力系数确定后，滑行阻力与车速的关系随之确定。根据GB/T 12534-1990《道路试验方法通则》中对气象条件的要求，滑行试验过程中的平均风速不能大于3 m/s，约合10.8 km/h。也有企业试验标准注明阵风最大风速不能超过5 m/s，约合18 km/h。利用方程(2)也可以计算出在顺风和逆风两种条件下的滑行距离，表5 列出了两个车型在120 km/h初速度滑行试验中，不同风速条件下的滑行距离。

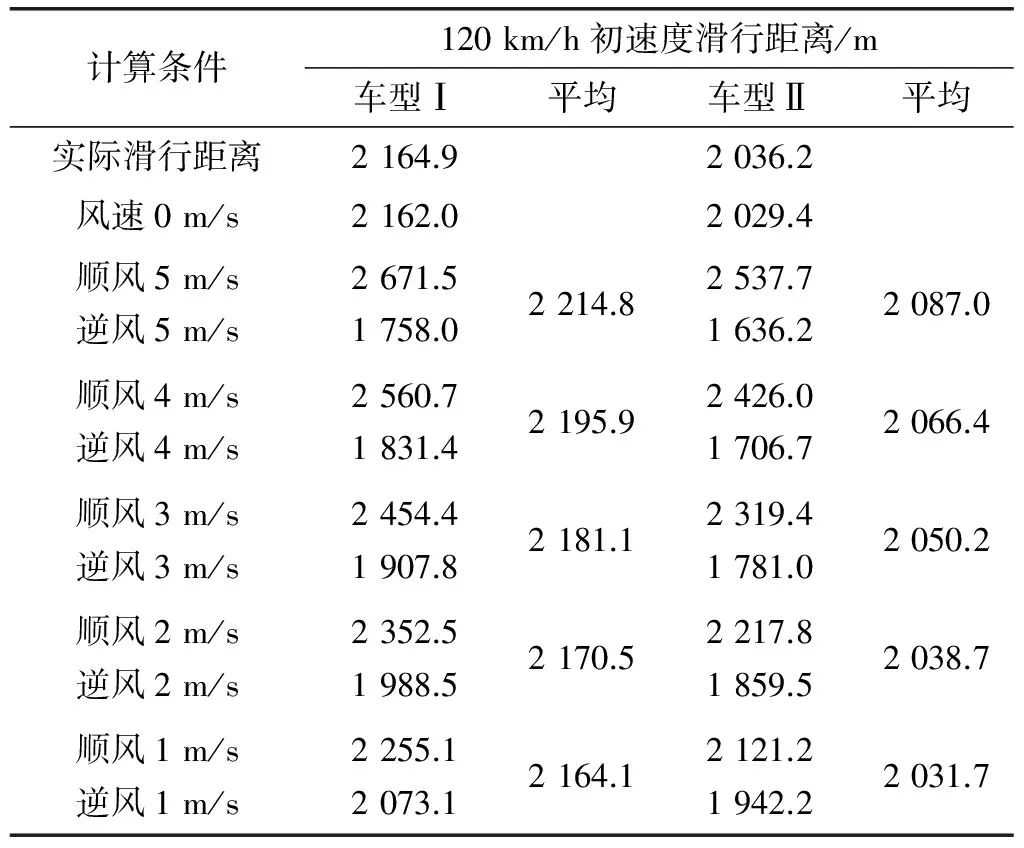
表5 120 km/h初速度滑行距离

GB/T 12536-1990 《汽车滑行试验方法》是我国专门的汽车道路滑行试验方法标准，该标准适用于各类汽车，滑行初速度为50 km/h。根据中机函[2010]145号文件，汽车新产品公告时，对滑行试验项目的检验依据仍然是上述标准，所以有必要考查各个风速对50 km/h初速度滑行距离的影响，计算结果见表6。

综合表5、表6的计算结果可以发现：两种初速度下的滑行实际距离与滑行理论计算距离几乎一致。如果在120 km/h初速度滑行试验中的风速一直处于3 m/s的状态，那么两个方向的滑行距离会相差26.5%；如果在50 km/h初速度滑行试验中的风速一直处于3 m/s的状态，那么，两个方向的滑行距离会相差8.5%，这说明，风速对较高的初速度滑行试验影响更大。随着风速越大，平均滑行距离越大，但各环境风速条件下的平均滑行距离相差不大。

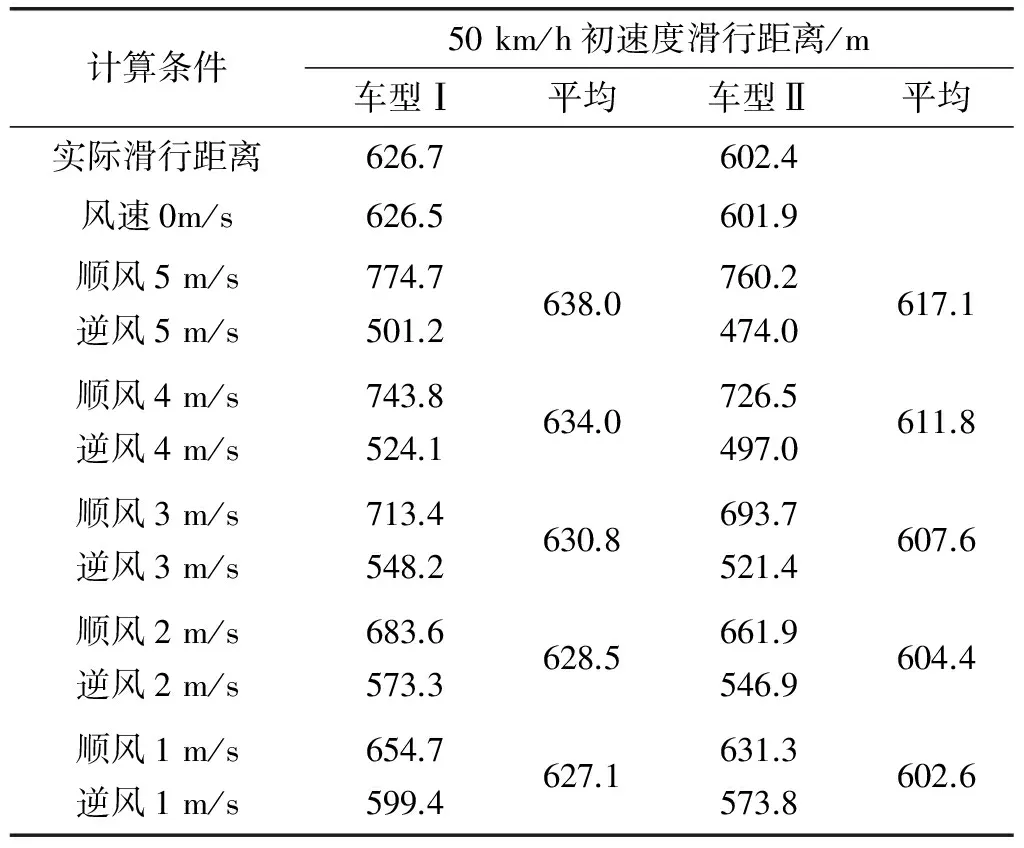
表6 50 km/h初速度滑行距离

4 结论

(1)在进行不大于120 km/h初速度时的滑行阻力拟合时，方程法与标准法具有几乎相同的拟合精度。虽然在理论上，方程法的拟合精度要高于标准法，但在实际操作中使用标准法是可接受的。

(2)道路滑行阻力常数项为车速为0时的滚动阻力。滑行阻力一次项系数不能省略，它是滚动阻力、传动系阻力受车速影响的综合体现。

(3)通过文中的实例，在符合试验条件的情况下，120 km/h初速度滑行试验中相反方向的滑行距离偏差可以高达26%的。为保证滑行试验结果的正确性，滑行试验需要进行多次，并且要剔除往返一次平均滑行距离过大的试验数据。

【1】余志生.汽车理论[M].3版.北京：机械工业出版社，2000.

【2】周荣宽，韩晓东，韩宗奇，等.基于道路试验的电动汽车滑行阻力系数分析[J].汽车技术，2015(4)：52-55. ZHOU R K，HAN X D，HAN Z Q，et al.Road Test Analysis of Coasting Resistance Coefficient for Electric Vehicle[J].Automobile Technology,2015(4):52-55.

【3】王博文，候永平，周毅，等.乘用车滑行阻力与传动系阻力的研究[J].汽车科技，2010(2)：24-27. WANG B W，HOU Y P，ZHOU Y，et al.Investigation on Coasting Resistance and Transmission Resistance of Passenger Car[J].Automobile Science & Technology,2010(2):24-27.

Compare between Two Methods on Coasting Data Processing and the Influence of Wind Velocity on Coasting Distance

SUN Tao, WANG Zhenlai

(Research & Development Center, FAW Co., Ltd., Changchun Jilin 130011,China)

Two different methods on coasting data processing were compared. Some affecting factors on the constant term, linear term and quadratic term in coasting resistance coefficient were investigated, and the basis that linear coefficient could not be omitted was given. At last, the influence levels of wind velocities on the coasting distance were compared.

Coasting resistance; Coasting resistance coefficient; Coasting data processing methods

2017-02-24

孙涛(1989—)，男，学士，助理工程师，研究方向为汽车性能试验。E-mail：st_crx@126.com。

10.19466/j.cnki.1674-1986.2017.06.001

U467.1

A

1674-1986(2017)06-001-04