基于改进的无尺度网络的高斯动态粒子群优化算法在舰船电网故障重构中的应用

陈洋， 刘彦呈， 王川

(大连海事大学 轮机工程学院，辽宁 大连 116026)

基于改进的无尺度网络的高斯动态粒子群优化算法在舰船电网故障重构中的应用

陈洋， 刘彦呈， 王川

(大连海事大学 轮机工程学院，辽宁 大连 116026)

针对当前优化算法在处理大规模舰船电网重构问题时易陷于局部极值的缺点，提出一种基于改进的无尺度网络的高斯动态粒子群优化(Gaussian Dynamic Particle Swarm Optimization, GDPSO)算法.该算法融合无尺度网络理论与种群拓扑结构，采用改进的无尺度网络BA模型随机地逐渐增加种群拓扑规模，增加种群多样性，提高种群跳出局部极值的能力.以某20节点和扩充为60节点的舰船电网为例进行故障后重构测试.结果表明，该算法对多维度舰船电网重构有效.

舰船电网； 故障重构； 高斯动态粒子群优化； 无尺度网络

0 引 言

舰船电力系统为舰船上很多设备提供动力.一旦舰船电网在某点故障，整个电网的安全可靠运行就可能受到影响，因此需要立即将故障隔离，并且快速生成重构方案，最大限度地保证重要负载的供电恢复，以确保舰船航行中的安全性.

BUTLER等[1]提出了一种专家系统与地理信息系统相结合的故障检测方法来实现船舶电力系统重构，其专家系统的完善经历了一个漫长的过程.文献[2]用遗传算法来搜索重构策略，但只考虑了负载恢复这一单目标问题，未考虑其他可能影响重构的因素.文献[3-4]采用一种机器学习算法来处理小型船舶电网重构的问题，进行了一系列假设，有一定局限性.文献[5]提出了一种小种群粒子群算法对船舶电网进行重构，文献[6]在此基础上提出动态小种群的概念，两篇文献均只验证了简单的船舶电网模型.文献[7]将“背包策略”和模拟退火算子与粒子群算法进行融合，该算法在操作中增加了重构的复杂性，从而拖长了重构所需时间.为应对复杂舰船电网重构问题的求解要求，本文提出一种改进的无尺度网络高斯动态粒子群优化(Gaussian Dynamic Particle Swarm Optimization, GDPSO)算法，该算法对种群拓扑结构进行改进，将无尺度网络理论融合到种群拓扑结构中，以增强种群多样性，从而更好地求解复杂的多目标优化问题.

1 舰船电网重构问题数学模型

1.1 舰船电网的网络拓扑

图1 某驱逐舰供电系统的符号示意图

表1 负载参数及负载等级

1.2 舰船电网重构问题的目标函数和约束条件

舰船电网在实际运行中如果出现故障或处于非正常运行状态，就需要快速准确地对故障进行处理.如果处理不当或者不及时，就有可能造成损失，危害整个舰船的安全性.舰船电网重构的主要任务就是在出现故障时，在满足运行约束条件的前提下，通过切换电网中的开关来保证重要负载的供电.若考虑1级、2级和3级负载的恢复，则其目标函数[2]为

(1)

式中：N1，N2和N3分别为1级、2级和3级负载的个数，负载总数NL=N1+N2+N3；P1i，P2j和P3k分别为1级、2级和3级负载的功率；λ1，λ2和λ3分别为1级、2级和3级负载的权重因数；xi,xj和xk分别表示1级、2级和3级负载的供电状态，xi(xj,xk)=0表示负载失电，xi(xj,xk)=1表示负载主线路供电，xi(xj,xk)=2表示负载备用线路供电.

为满足负载恢复最大的目标，同时要考虑目标的优先级，必须保证优先等级高的负载先恢复供电.为此，将负载的权重因数赋予不同的值.考虑操作自动开关和手动开关，目标函数可以表示为

(2)

式中：yG，yM和yA分别表示故障后舰船电网负载恢复过程中操作发电机出口开关、手动开关和自动开关的总数；kG，kM和kA分别为对应的权重因数，kG>kM>kA.

本文中考虑两个约束条件：系统的容量约束和连接性约束.容量约束是指当系统出现故障，重构方案中负载转移时，不能引起支路或发电机的过载(如果过载，则必须先选择卸掉部分非重要负载).

(3)

式中：xij=0或1，表示连接开关的断开或接通；Si为负载或支路的用电量；Mj为支路j的容量裕度.连接性约束是指对于有备用路径供电的负载，正常供电路径和备用路径有且仅有一条能够闭合.

(4)

式中：Ωi为转换开关集合；zk和zl分别表示同一负载的正常开关和备用开关的工作状态，zk，zl=0或1，0表示断开，1表示接通.

2 改进无尺度网络GDPSO算法

2.1 GDPSO算法的由来

粒子群优化算法自1995年被提出后，一直被不断改进.文献[8]提出一种信息全部共享的粒子群(Fully Informed Particle Swarm，FIPS)算法，该算法利用邻居节点的最优信息进行粒子速度的迭代.对FIPS算法进行进一步改进，就形成了GDPSO算法.GDPSO算法迭代公式为

(5)

(6)

(7)

式中：W1和W2均为权值，一般取W1=0.729，W2=2.187；G(0, 1)为一个高斯随机数；k表示粒子i的邻居节点的标号；K表示粒子i的邻居节点的个数；pid表示粒子i的当前最优值；pkd表示粒子i的邻居节点的最优值.

GDPSO算法中粒子每次迭代都会调用粒子自身和邻域粒子的最优信息，这使得算法性能受邻域拓扑结构影响很大，因此需要合理选择拓扑结构以提高算法性能.

2.2 无尺度网络的改进策略

改进的无尺度网络拓扑结构由两部分组成：rand-5静态拓扑结构[9]和无尺度网络拓扑结构.rand-5静态拓扑结构是一种平均度为5，度分布标准偏差小于3的随机生成的静态拓扑结构.

随着复杂网络研究的兴起，无尺度网络的概念被提出.BARABASI等[10]通过分析万维网发现，其度分布遵守幂律分布，将这种网络称为无尺度网络.最初的幂律分布的网络结构模型被称为BA模型，该模型有两个最主要的生成机制——增长机制和择优连接机制.增长机制：初始网络G0较小，初始网络的节点数量为m0，每经过一固定的时间步长Δt，网络添加1个具有m(≤m0)条边的新节点，与m个已经存在的不同的节点相连.择优连接机制：在新节点加入过程中，新节点优先考虑连接度值更高的节点.定义pi为新添加的节点连接到原始网络节点i的概率，则pi值取决于节点i的度ki，即

(8)

定义Δt的增加次数r与迭代次数i之间的关系为mod(i/r)=n，其中r=0，1，…，N-m0，n表示时间步长控制系数，N表示粒子总数.一般来说，r≠i.每增加一次时间步长后都有一个新的非活跃粒子被激活连接到网络中，r计数加1，增加r次时间步长后，得到的新网络节点数就增加至m0+r.随着r值的增大，该网络进入尺度不变的状态，尺度指数为γ=2.9±0.1，与模型中唯一的参数m无关.为适当提高低度数粒子的信息传递速度，从而提高算法精度和成功率，在每次时间步长里都增加1次粒子间的连接机会，设定平均度最高的粒子jh与平均度最低的活性粒子jl相连的概率为p(r)=1.这样的修正仍然遵守无尺度网络幂律分布特性.

图2描述了一个简单的无尺度网络的生成过程.初始活跃节点数m0=2，每次增加1个节点j与m(=2)个粒子建立连接.当遇到两个粒子的度值一样时，节点j随机选取其中一个粒子与其连接.

图2 无尺度网络的生成过程

3 改进的无尺度网络GDPSO算法应用于舰船电网重构的仿真流程

将改进的无尺度网络拓扑结构与GDPSO算法结合，就构成了改进的无尺度网络GDPSO(Improved Scale-Free GDPSO, ISFGDPSO) 算法.ISFGDPSO算法流程见图3.

4 舰船电网重构仿真算例分析

本文采用图1所示的舰船电力系统模型，故障前所有负载均由常规供电路径供电.设置算例1：某一时刻，支路19和57发生故障.设置算例2：为验证当电网规模扩大时算法的有效性，将图1电网模型所有参数扩大到原来的3倍，负载个数增加到60个(分别记为L1-1～L20-1，L1-2～L20-2和L1-3～L20-3)，增加的负载和原负载在供电线路、负载等级以及负载容量上都保持一致；发电机容量也增加到原来的3倍；某一时刻L5-1，L15-1，L5-2，L15-2的常规供电线路出现故障.

图3 ISFGDPSO算法流程

设置最大种群规模N=50，每个算法执行31次，最大迭代次数为3 000次.为进行对比，选用5种算法与本文提出的ISFGDPSO算法进行对比.选用的5种算法分别为DGA(免疫遗传算法)[2]、SWPS-s算法(小世界网络粒子群算法)[11]、R3PS算法(小生境粒子群算法)[12]、DNSPS算法(带邻居搜索的粒子群算法)[13]和SFIPS算法(无尺度FIPS粒子群算法)[14].

图4为采用这6种算法得到的适应度值中值收敛曲线.由图4a)可以看出，ISFGDPSO算法能够在较小的迭代步数内搜索到最小的适应度值，比其他5种算法的收敛速度快.表2记录了算例1中采用这6种算法得到的适应度值的最小值、中值、最大值、平均值及其标准偏差值.由表2可以看出，ISFGDPSO算法在适应度值上的表现明显好于其他算法，从标准偏差值对比也能看出，其具有最好的数值稳定性.表3记录了对算例1进行仿真生成的故障状态下的最终重构方案.由表3可以看出，ISFGDPSO算法失电负载最少，虽然它比DGA多了几次开关操作，但少了一个2级负载失电.综合考虑，ISFGDPSO算法的重构方案更为合理.

a)算例1

b)算例2

算法最小值中值最大值平均值标准偏差值DGA0.0940.1680.5320.1640.204R3PS算法0.1340.2020.3870.2130.139SFIPS算法0.0970.2010.4280.1870.156DNSPS算法0.0820.1810.2860.1780.102SWPS-s算法0.1630.2230.5430.2320.231ISFGDPSO算法0.0710.1480.2610.1460.094

表3 算例1重构方案

由图4b)可以看出，虽然个别其他算法在最初的迭代过程中收敛很快，但ISFGDPSO算法最终收敛效果最好.表4记录了算例2中采用这6种算法得到的适应度值的最小值、中值、最大值、平均值及其标准偏差值.由表4可以看出：适应度值的中值和平均值的最优值均是由ISFGDPSO算法获得的，说明该算法有较好的收敛性能；适应度值的标准偏差最小值也是由ISFGDPSO算法获得的，说明该算法的数值稳定性相对更好.

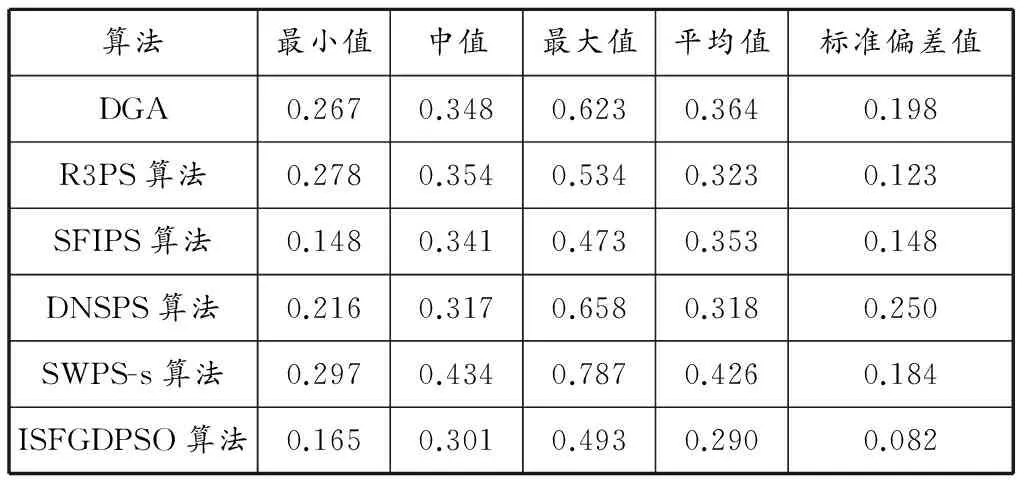
表4 算例2适应度值

表5记录了对算例2进行仿真得到的重构方案的最终结果.由表5可以看出：DGA的最优重构方案虽然具有最少的开关操作次数，但卸载了重要负载，对重构效果影响较大，并且该算法不是每次都能收敛，导致平均迭代次数较大；其他5种算法中，ISFGDPSO算法最优方案中卸载的负载个数和开关操作次数都是最少的，并且具有最小的平均迭代次数，说明ISFGDPSO算法在该算例中具有最好的优化性能.

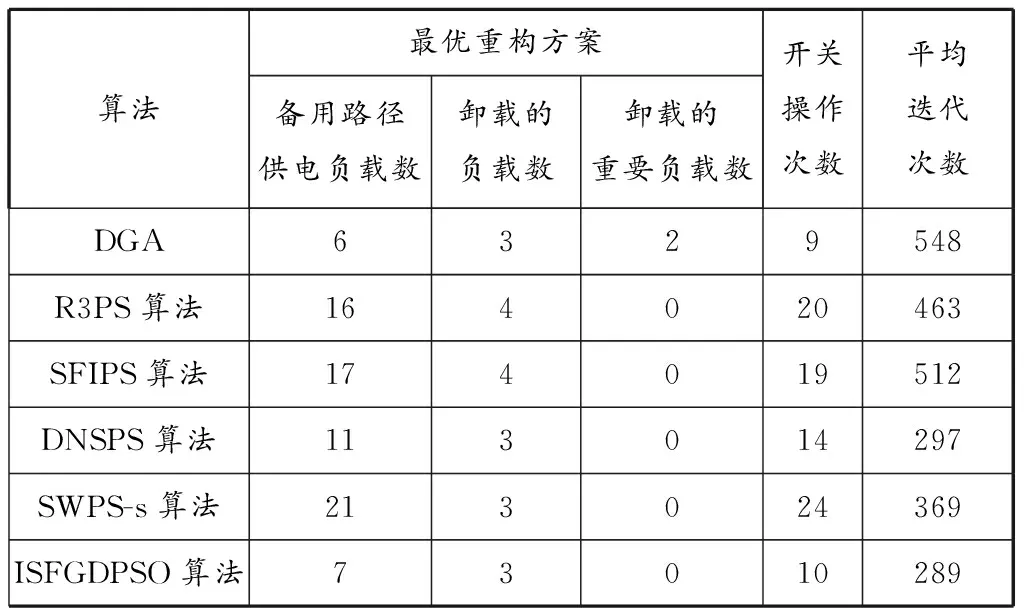
表5 算例2重构方案

5 结 论

针对高维度、多目标的舰船电网的故障重构模型，给出一种改进的无尺度网络高斯动态粒子群优化(ISFGDPSO)算法，用无尺度网络的BA模型构造算法的种群拓扑结构，从而增加粒子群的种群多样性，避免粒子群过早陷入局部极值，满足优化目标的重构要求.仿真结果表明，改进的无尺度网络拓扑结构能够有效增加种群多样性，满足高维度舰船电网故障后的重构要求.

[1]BUTLER K L, SARMA N D R, WHITCOMB C,etal. Shipboard systems deploy automated protection[J]. IEEE Computer Applications in Power, 1998, 11(2): 31-36.

[2]杨秀霞, 张晓锋, 张毅, 等. 基于启发式遗传算法的舰船电力系统网络重构研究[J]. 中国电机工程学报, 2003, 23(10): 42-46.

[3]DAS S, BOSE S, PAL S,etal. Dynamic reconfiguration of shipboard power systems using reinforcement learning[J]. IEEE Transactions on Power Systems, 2013, 28(2): 669-676.

[4]BOSE S, PAL S, NATARAJAN B,etal. Analysis of optimal reconfiguration of shipboard power systems[J]. IEEE Transactions on Power Systems, 2012, 27(1): 189-197.

[5]MITRA P, VAYAGAMOORTHY G K. Implementation of an intelligent reconfiguration algorithm for an electric ship’s power system[J]. IEEE Transactions on Industry Applications, 2011, 47(5): 2292-2300.

[6]WANG C, LIU Y C, ZHAO Y T. Application of dynamic neighborhood small population particle swarm optimization for reconfiguration of shipboard power system[J]. Engineering Applications of Artificial Intelligence, 2013, 26(4): 1255-1262.

[7]陈雁, 孙海顺, 文劲宇, 等. 改进粒子群算法在船舶电力系统网络重构中的应用[J]. 电力自动化设备, 2011, 31(3): 29-34.

[8]MENDES R, KENNEDY J. The fully informed particle swarm: simpler, maybe better[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 204-210.

[9]CHEN Y, LIU Y C, WANG C,etal. Associations between population topologies and Gaussian dynamic particle swarm performance[J]. International Journal of Modelling, Identification and Control, 2015, 24(2): 138-148.

[10]BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286: 509-512. DOI: 10.1126/science.286.5439.509.

[11]KIRLEY M, STEWART R. Multiobjective evolutionary algorithms on complex networks[J]. Evolutionary Multi-Criterion Optimization, 2007, 4403: 81-95.

[12]LI Xiaodong. Niching without niching parameters: particle swarm optimization using a ring topology[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(1): 150-169.

[13]WANG Hui, SUN Hui, LI Changhe,etal. Diversity enhanced particle swarm optimization with neighborhood search[J]. Information Sciences, 2013, 223(2): 119-135.

[14]ZHANG C G, YI Z. Scale-free fully informed particle swarm optimization algorithm[J]. Information Sciences, 2011, 181: 4550-4568.

(编辑 贾裙平)

Application of Gaussian dynamic particle swarm optimization algorithm based on improved scale-free network in fault reconfiguration of ship power system

CHEN Yang, LIU Yancheng, WANG Chuan

(Marine Engineering College, Dalian Maritime University, Dalian 116026, Liaoning, China)

To overcome the shortcoming that the existing optimization algorithm is prone to a local extremum when dealing with large-scale reconfiguration issues of ship power system, Gaussian Dynamic Particle Swarm Optimization(GDPSO) algorithm based on the improved scale-free network is proposed. This algorithm integrates the scale-free network theory with the population topology structure. It adopts the modified BA model of scale-free network to increase the scale of population topology randomly, which can increase the population diversity and improve the ability of population jumping out of the local extremum. Fault reconstruction tests are run with the cases of a 20-node ship power system and an expanded 60-node ship power system. Results show that the proposed algorithm is effective for multi-dimensional ship power system reconfiguration.

ship power system; fault reconfiguration; Gaussian dynamic particle swarm optimization; scale-free network

10.13340/j.jsmu.2017.01.016

1672-9498(2017)01-0079-05

2016-02-06

2016-04-29

辽宁省自然科学基金(2014025006)

陈洋(1980—)，女，湖南常德人，工程师，博士，研究方向为智能算法和船舶电力系统优化控制，(E-mail)shangruihan@163.com； 刘彦呈(1963—)，男，辽宁大连人，教授，博导，博士，研究方向为船舶电力推进、船舶机电一体化和新能源利用，(E-mail)liuyc@dlmu.edu.cn

U665.12

A