多箱区多场桥调度优化模型及算法实现

初良勇， 李淑娟， 阮志毅

(1. 集美大学 航海学院，福建 厦门 361021； 2. 仰恩大学 管理学院，福建 泉州 362000； 3. 海南师范大学 数学与统计学院，海口 571158；4. 厦门雅迅网络股份有限公司，福建 厦门 361008)

多箱区多场桥调度优化模型及算法实现

初良勇1， 李淑娟2， 阮志毅3,4

(1. 集美大学 航海学院，福建 厦门 361021； 2. 仰恩大学 管理学院，福建 泉州 362000； 3. 海南师范大学 数学与统计学院，海口 571158；4. 厦门雅迅网络股份有限公司，福建 厦门 361008)

为探究在预知集卡进场时间与运载任务的条件下，如何低成本、高效率地对多场桥进行调度这一难题，本文以多箱区多场桥调度为研究对象，以场桥移动成本与时间窗下场桥与集卡之间的等待罚金之和最小为目标，以场桥间作业安全距离为约束，并考虑场桥作业时间的均衡性，建立数学模型.利用模拟退火算法对模型进行求解，并利用MATLAB实现算法编程.根据某港口的实例数据，通过应用程序进行多场桥调度的算法求解.求解结果与实际人工操作相比，运作成本大幅降低，作业时间也缩短，这验证了本文调度优化模型及其实现算法的有效性与显著性.

多箱区； 多场桥； 移动成本； 等待罚金； 模拟退火算法

0 引 言

场桥是集装箱堆场上重要的装卸设备，场桥与内外集卡的顺利衔接，对整个堆场物流系统乃至整个港口集装箱物流系统起着巨大的推动作用.国内外关于场桥调度优化问题的研究成果丰硕，大多数研究集中在优化场桥的移动轨迹、操作次序和配置数量等方面.KIM等[1]以单个龙门吊为研究对象，研究了外集卡的交箱和取箱任务的作业序列问题.KIM等[2]考虑不同限制条件对场桥操作的影响，建立了混合整数规划模型，并采用分支定界法和贪婪随机自适应搜索算法进行求解.NG等[3]以龙门吊的等待时间最小为目标，利用分支定界法对模型的有效性进行验证.贺茂英[4]建立了单台龙门吊和多台龙门吊的路径优化模型，利用改进的模拟退火算法对模型进行求解.杨曼[5]以龙门吊最短作业时间为目标建立了数学优化模型，并运用近邻策略的遗传算法进行求解，通过实例验证了模型和算法的有效性.郑红星等[6-8]对混堆箱区的场桥调度问题展开了细致的研究，先后对单箱区单场桥的调度问题、多箱区多场桥的调度问题、考虑外集卡等待时间的场桥调度问题进行了研究，并根据各模型的特点设计智能算法进行求解，最后运用实例验证了模型的有效性.

随着信息技术的不断发展，很多港口已实现外集卡进场提前预约，这使得场桥的调度问题有了进一步优化的空间，但当前大多数的参考文献并未考虑这一因素.本文引入时间窗，设定外集卡期望被服务的时间窗，并同时考虑场桥的移动时间成本，对场桥等待集卡和集卡等待场桥的时间进行优化.

1 模型建立

本文针对堆场的实际情况，建立多箱区多场桥调度模型，对调度过程进行优化使得场桥调度时间成本和费用成本最低，并着重于均衡各场桥的作业时间.

1.1 问题提出

在实际的堆场中，因为场桥体积大且成本高，通常场桥的配置数量是少于堆场的箱区数量的，所以经常会出现场桥转场的情况.场桥的转场是通过转动轮胎90°实现的，通常每次转场都要花费至少5 min的时间，箱控室在安排场桥操作任务时都会尽量避免场桥转场(一般就近安排场桥)，因此经常会出现有的箱区场桥工作繁忙，而有的箱区场桥闲置的情况.箱控室对场桥的调度没有具体的调度规则，场桥调度受人的因素影响较大.本文以场桥转场时间、集卡等待时间和场桥等待时间最短为目标，以场桥移动成本最少和时间窗内场桥等待集卡和集卡等待场桥的罚金最小为目标，同时考虑场桥与场桥之间作业时间的均衡性，建立相应的数学模型，以获取最优的任务调度方案.本文所研究的箱区布局见图1.

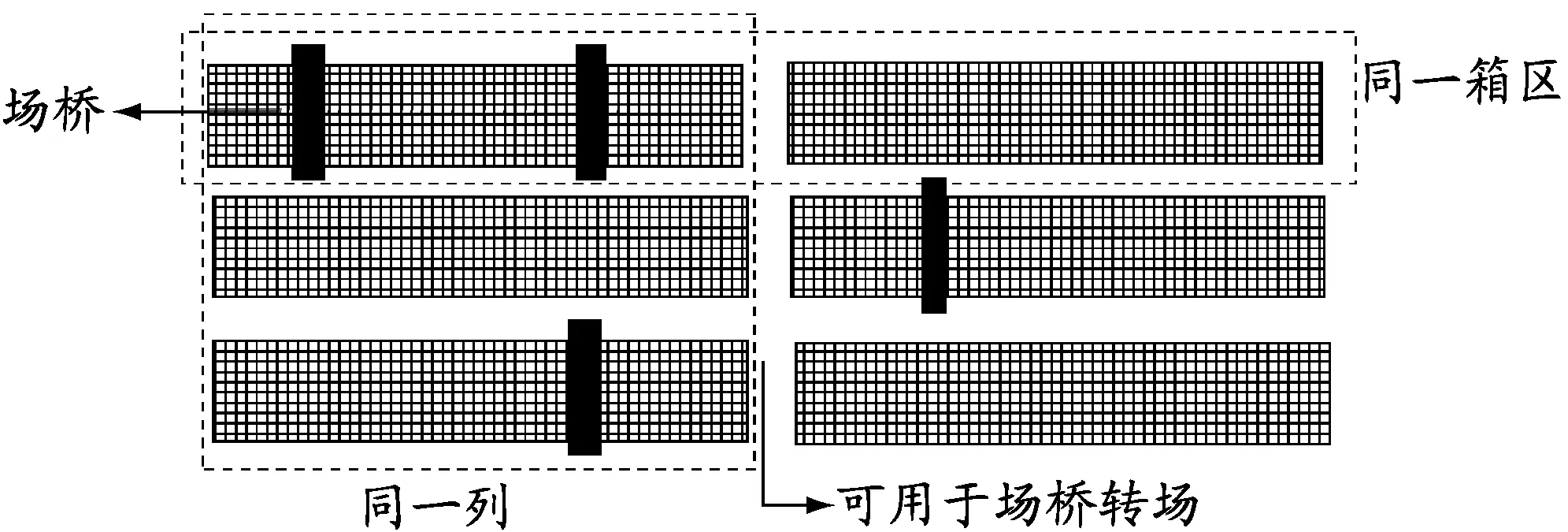
图1 集装箱堆场俯视图

1.2 模型假设

(1)堆场上场桥的操作任务都以20英尺标准集装箱(TEU)为单位；(2)场桥移动速度以及转场时轮胎转动90°的时间是固定的；(3)每台场桥的移动成本相同，忽略设备老旧可能导致的能耗的不同；(4)在同一箱区内操作的场桥之间必须保持一定的距离以保证安全；(5)计划期内场桥待操作任务总数远多于场桥的数量；(6)场桥初始时刻位于其初始操作任务所在的贝位处，且操作完最后一个任务后即停在原地直至所有场桥作业结束；(7)场桥操作完一个任务后，随即移动至下一个任务所在的贝位处，且沿最短路径移动；(8)计划期内场桥的任务量、任务所在位置、集卡到达时间以及场桥操作任务的时间都是已知的；(9)忽略场桥司机技术的娴熟程度，即每个任务被任一场桥操作的时间长度都是相同的；(10)堆场列间过道两侧的贝位数相同，且箱区间过道宽度为一个贝位，列间过道宽度为两个贝位；(11)场桥可通过列间过道和两侧过道进行转场，其中列间过道可同时通过两个场桥，两侧过道仅可通过一个场桥.

1.3 模型相关参数说明

模型中基本参数的设定见表1.

根据堆场、任务与贝位等初始信息，场桥从任务

表1 模型中的基本参数

i到任务j的移动距离可表示为

其中，任务之间位置的示性函数为

从而可得场桥从任务i到任务j的移动时间为

不失一般性，本文假设场桥k有操作任务p和q，并且其操作次序为p→q，即xpqk=1，则场桥到达任务q的时刻为sqk=Fpk+Tpq，任务操作结束的时刻为Fqk=Tq+max{sqk,Rq}.

1.4 目标函数

本文以场桥移动成本和场桥、集卡等待罚金最小为目标，并考虑场桥之间作业时间的均衡性，建立调度优化模型，其目标函数为

(1)

式中：场桥k对于任务i和j的示性函数为

场桥和集卡等待时间的惩罚函数为

场桥k对于任务i的示性函数为

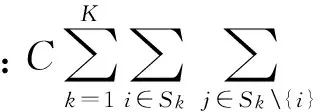
1.5 约束条件

(2)

(3)

(4)

Nk>1，k=1,2，…，K

(5)

(6)

(7)

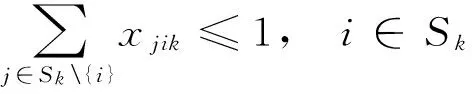
(8)

i∈Sk；k=1,2,…,K

(9)

xijk≤ωikωjk，i,j=1,2,…，N；k=1,2,…K

二是深化市场经济体制改革。全要素生产率增长的源泉主要有两个：技术进步和资源配置效率的改进，从中国目前来看，资源配置效率改进最大的动力就是市场经济体制改革。因此，应进一步推动和完善市场配置资源的制度，营造公平竞争的经济环境，为全要素生产率的提高创造制度空间。

(10)

(11)

式(2)表示所有场桥操作任务总数为N；式(3)表示由场桥k操作的任务数为Nk；式(4)表示每个任务由且仅由一个场桥操作；式(5)表示堆场上的每个场桥操作的任务多于1个，基于待操作任务总数远多于场桥数量这一假设，此约束条件并不会影响模型的最优化求解，同时它还是式(9)成立的前提；式(7)表示任意由场桥k操作的任务i,至多存在某个任务p使得操作次序为i→p；式(8)表示任意由场桥k操作的任务i,至多存在某个任务q使得操作次序为q→i；式(9)表示任意由场桥k操作的任务i,至少存在某个任务p使得操作次序为i→p,或者至少存在某个任务q使得操作次序为q→i；式(10)是对变量ωik和xijk定义的刻画；约束条件(11)表示任意时刻不同场桥之间必须保持在相互的安全距离之外.式(6)～(10)构成模型的子回路消除约束和流入流出约束.

2 算法设计

本文所研究的问题属调度遍历问题，其求解主要可分为精确解法和近似解法.当此类NP难问题规模较大时，一般采用启发式算法进行求解.本文采用模拟退火算法求解.事实上，对车辆路径问题的求解，一般会优先考虑模拟退火算法.这是因为模拟退火算法具有通用易实现以及对初始点稳定性好的优点，且该算法具有全局搜索的特点，理论上它总能够100%地收敛到全局最优解.结合所建立的优化模型，下面对相关的参数与规则进行设定.

2.1 解的表现形式

首先，将进场的外集卡进行编号，形成一条任务顺序链，即1,2,…,N.然后，对任务以一定次序分配给K个场桥，每个场桥均得到一组任务编码.最后，根据编码代表的操作次序对相应场桥进行调度.本文采用两个变量表示解的编码，其中一个编码为所有任务号，另一个编码为分配给场桥的相应任务量.例如图2表示两个场桥分别以9→4→2→1→8和7→3→5→6的次序操作对应任务，即根据任务量变量依次序将任务号分割成[9-4-2-1-8]和[7-3-5-6].

a)任务号b)任务量

图2 解编码方式的表示

2.2 初始解的产生

运用蒙特卡洛方法进行若干次模拟，并选择其中最优的解作为算法的初始解.在蒙特卡洛模拟过程中：先随机选出K个任务分配给K个场桥，作为其初始操作任务;然后，对照初始操作任务，按就近原则将剩下的任务逐一地分配给相应的场桥.这样既可以最大程度地使模拟解满足式(11)，又能够使模拟退火算法以较快的速度收敛到最优解.

2.3 邻域解的产生

本文中邻域解的产生有两种方式:(1)在每个场桥分配到的任务中，任意选取两个任务互换其操作次序，以生成新的邻域解，如图3中操作次序[3-4-2-1-5-7-6]的3个不同互换形式;(2)为均衡各场桥的作业时间，将作业时间最长的场桥的最后一个任务调配给作业时间最短的场桥，作为其最后一个操作任务，从而形成新的邻域解.以上这两种方式的邻域解产生概率相等.

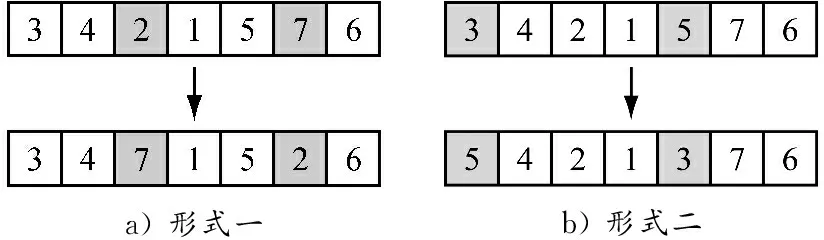
a)形式一b)形式二

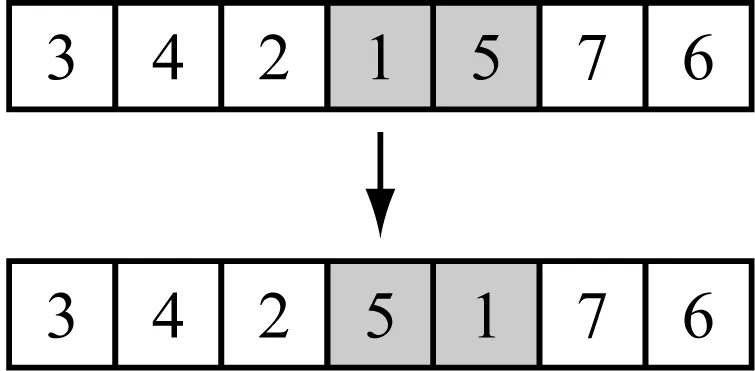
c) 形式三

2.4 相关参数的设定

设置初始温度t0，终止温度te和降温因数α(0<α<1).同时，设定降温函数为tm=αtm-1.在降温过程中，以概率接受新产生的邻域解，即若满足

(12)

则接受邻域解，其中，r～U[0,1]，ΔZ为邻域解与当前解的目标函数差值，tm为当前温度.当前温度低于终止温度时终止算法，即只要满足tm

然而，蒙特卡洛模拟得到的解以及产生的邻域解可能不满足式(11).为使算法在一定程度上难以接受不满足式(11)的邻域解，以目标函数值与一个大于1的数γ相乘(即γZ)作为惩罚.

对于初始解与邻域解，由初始时刻起每隔一定的时间步长对场桥进行一次定位，并计算各场桥之间的距离，以判断对应的解是否满足式(9).显然，所取的时间步长必须小于Bsafe/v.

3 实例验证

通过采集某港口实际运营数据，验证本文所建立的模型以及用于求解模型的启发式算法的有效性.选取该港口3个出口箱区中在75 min内到达的集卡的40个任务，具体数据见表2.

该箱区左右两侧各有30个贝位，中间过道和两侧都有场桥的转场板.在模型中，假定集卡期望在其到达的30 min内被服务，即TLi=TEi+30.可以根据码头管理者的偏好设定场桥等待时间和集卡等待时间的罚金，若是更倾向于码头的运营成本，则可以设置.场桥和集卡的相关参数见表3.

表2 算例数据

表3 场桥和集卡的参数设定

设定场桥之间作业时间均衡性函数的调节因数λ为1/8，以及γ为1 000.进行1 000次蒙特卡洛模拟，得到初始解，其目标函数值为90 697.082 2单位.同时，设置初始温度为5 000 ℃，终止温度为100 ℃，降温因数为0.999 9.利用模拟退火算法由初始解分别进行3次迭代求解，经过若干次接受邻域解的迭代，得到算法在降温过程中的“最优解”.对该港口实际人工操作次序与算法所得的最优解及其目标函数值进行比较，结果见表4.

由表4可知：通过模拟退火算法对本文调度优化模型进行编程，3次迭代求解结果的目标函数值均远小于实际人工操作的目标函数值；从这3次迭代求解的结果看，除了场桥操作任务的次序略有区别之外，优化后两个场桥所分配到的任务是完全相同的.本文中由移动成本与等待罚金之和所组合的目标函数，要求优化模型综合考虑集卡到达时间和任务所处贝位等信息进行求解.对于后者，本文给出了两种邻域解的产生方式，显然其中用于调配任务的邻域解产生方式已达到预设的目的，而另外一种原本希望能够以较快的速度收敛到“最优解”的邻域解产生方式，在其即将趋近于“最优解”时容易造成移动距离或等待罚金增大或者使场桥间作业时间的不均衡程度扩大，从而难以收敛到“最优解”.针对这个问题，在优化程序中设置将解保存为句柄变量，使其可在各控件的返回函数中传递，即在每次降温过程中对当前最优解进行保存，从而可以进行多次模拟退火过程，通过反复迭代收敛到“最优解”.

因为γ取值1 000，且初始温度值远小于初始解的目标函数值，所以在降温过程中算法几乎不可能接受不满足式(11)的邻域解.不难看出，与用调度优化模型得到的结果比较，实际人工调度的操作次序轨迹具有更多的移动路程和转场次数.同时，实际人工调度需要超过190 min才能完成所有任务的操作，而运用调度优化模型大约用120 min即可完成，节省了大量的作业时间.由此可以得出结论，本文所建立的模型以及所运用的算法，在多箱区多场桥的调度优化上效果显著.

表4 实际人工调度与求解调度优化模型得到的结果比较

4 结论与展望

对当前多箱区间场桥的调度问题进行研究，建立多箱区多场桥的调度优化模型，通过优化调度过程实现场桥调度移动成本和场桥、集卡之间等待罚金之和的最小化，并运用模拟退火算法求解该模型，利用MATLAB实现算法的编程，最后利用实例数据对模型和算法的有效性进行验证.从实例验证的结果中可以看出，多箱区多场桥的调度优化模型能够有效避免场桥之间的安全距离问题，避免移动过程中不必要的等待时间，并且可以有效均衡场桥之间的作业时间，使得场桥司机的作业效率得到保障，这对场桥的实际操作具有现实意义.在实际的操作中，场桥的工作效率不只受场桥的移动轨迹和对任务操作次序的影响，因此对堆场布局、场桥调度和算法优化进行综合性研究将是下一阶段的工作重点，例如:(1)邻域解.对第3部分实例验证中所给邻域解的产生方式不足之处，可适当考虑增加或改进邻域解的产生方式，并对它们的产生概率进行调整，从而在确保收敛性的条件下，提高算法收敛于“最优解”的速度.(2)移动路径.本文假设场桥在任务的贝位间沿最短路径移动，这容易造成所产生的解多数并不满足安全距离，尤其是在场桥数量相对较多的时候，此时可以考虑在相同的转场情况下提供多条移动路径，并根据它们的移动距离以随机的形式对路径再次进行选择.(3)启发式算法.本文采用模拟退火算法对优化调度模型进行编程求解，但是由于模拟退火算法求解过程中仅考虑单一状态，很大程度上限制了算法求解的收敛速度，因此可以融入如遗传算法、粒子群算法、差分进化算法等种群、族群的特性，提高算法收敛效率与性能.(4)堆场.本文主要针对图1类型的集装箱堆场进行研究，然而，实际的港口堆场并不像图中箱区那样有规则性地堆放集装箱，因此还可以在不规则的堆场布局下，对多箱区多场桥的调度优化进行建模并实现.

[1]KIM K H, LEE K M, HWANG H. Sequencing delivery and receiving operations for yard cranes in port container terminals[J]. International Journal of Production Economics, 2003, 84(3): 283-292.

[2]KIM K H, KIM K Y. An optimal routing algorithm for a transfer crane in port container terminals[J]. Transportation Science, 1999, 33(1): 17-33.

[3]NG W C, MAK K L. Yard crane scheduling in port container terminals[J]. Applied Mathematical Modelling, 2005, 29: 263-267.

[4]贺茂英. 集装箱堆场龙门吊路径优化问题研究[D]. 大连: 大连海事大学, 2010.

[5]杨曼. 集装箱码头堆场资源优化配置与调度研究[D]. 大连: 大连海事大学, 2011.

[6]郑红星, 于凯. 基于混合遗传算法的混堆箱区内场桥调度研究[J]. 交通运输系统工程与信息, 2013,13(5): 150-158. DOI:10.16097/j.cnki.1009-6744.2013.05.025.

[7]郑红星, 于凯. 混堆集装箱箱区场桥调度模型与算法[J]. 计算机工程与应用, 2015, 51(3): 254-259. DOI: 10.3778/j.issn.1002-8331.1303-0464.

[8]郑红星, 吴岳, 杨文滔, 等. 混堆模式下多箱区场桥联合调度[J]. 水运工程, 2015(4): 113-119. DOI:10.16233/j.cnki.issn1002-4972.2015.04.021.

(编辑 贾裙平)

Scheduling optimization model and algorithm implementation of multiple container blocks with multiple yard cranes

CHU Liangyong1， LI Shujuan2, RUAN Zhiyi3,4

(1. Navigation College, Jimei University, Xiamen 361021, Fujian, China; 2. Management College, Yang’en University, Quanzhou 362000, Fujian, China; 3. School of Mathematics and Statistics, Hainan Normal University, Haikou 571158, China; 4. Xiamen Yaxon Network Co., Ltd., Xiamen 361008, Fujian, China)

To explore such an intractable issue as the scheduling of multiple yard cranes with low cost and high efficiency under the condition that the arrival time and task of container trucks are known beforehand, the scheduling issue of multiple container blocks with multiple yard cranes is studied. A mathematical model is established, where the objective is to minimize the cost including the moving cost of yard cranes and the fine of waiting between yard cranes and container trucks under the time window, the constraint is the safety distance of yard crane operating, and the balance of operating time among yard cranes is considered. The model is solved by the simulated annealing algorithm, and the programming of the algorithm is realized by MATLAB. The real data of a certain port are used as an example to carry out the algorithm for the scheduling solution of multiple yard cranes. Compared with the actual manual operation, the solution shows that the operating cost is reduced greatly and the operating time is shortened, which verifies the validity and the significance of the scheduling optimization model and its algorithm.

multiple container block; multiple yard crane; moving cost; fine of waiting; simulated annealing algorithm

10.13340/j.jsmu.2017.01.008

1672-9498(2017)01-0037-06

2016-05-22

2016-11-09

福建省自然科学基金(2017J01796，2017J01797)；福建省教育厅中青年教师教育项目(JA15288)；福建省厦门市科技项目(3502Z20143022,3502Z20113032)

初良勇(1973—)，男，黑龙江讷河人，副教授，博士，研究方向为集装箱物流系统优化与管理，(E-mail)chuliangyong@163.com

U691.34

A