指派问题的等价问题研究
鲍培文
(特警学院教学科研部,北京102211)
指派问题的等价问题研究
鲍培文
(特警学院教学科研部,北京102211)
任何一个指派问题有多个解决问题的渠道,每种渠道都对应一个新指派问题,这个新指派问题与原指派问题等价,即指派问题有多个等价问题.本文系统研究了每一指派问题的等价问题及其解法,找出不同解法之间的关系,有利于决策者快速准确进行指派问题的最优分配.
指派问题;等价问题;研究
在日常管理工作中,往往会碰到这样的人员分配问题:有n项任务(或工作)A1,A2,…An,需要给n个人B1,B2,…,Bn去完成,每人只能执行一项任务.由于每个人完成每一项任务的时间(或效率)不尽相同,所以对不同的分配方案,完成任务的总时间(或总效率)也不同.如何分配某人去完成某项任务,才能使完成n项任务的时间最少(或总效率最高),这就是指派问题,它包括标准指派问题和非标准指派问题.标准指派问题是人数与事数相等、一人一事及一事一人的最小费用问题.日常活动中也不乏人数与事数可以不等、一人多事及一事多人的情形,这类事务呈现了指派问题非标准的实际背景.非标准指派问题是人数与事数不等,或指定一人某事、某人一事,或一人多事、一事多人,或最大效益的指派问题.由于指派问题种类繁多,模型特殊,任何一个指派问题有多个解决问题的渠道,每种渠道都对应一个新指派问题,这个新指派问题与原指派问题等价,即指派问题有多个等价问题.本文系统研究了每一指派问题的等价问题及其解法,找出不同解法之间的关系,有利于决策者快速准确进行指派问题的最优分配.
1 指派问题及其解法
1.1 问题及其模型
任务分配与工作指派问题简称为分配问题或指派问题(Assignment Problem).标准指派问题是:每项工作只能分配给一个单位(人或武器)去完成;每个单位(人或武器)只能接受其中一项任务的最小费用问题.标准指派问题的数学模型为:


这时称目标函数的系数所构成的矩阵为费用矩阵或系数矩阵;满足约束方程的解xij(i,j=1,2,…,n)构成的矩阵X=(xij)n×n为解矩阵.
从以上模型可见,指派问题是一类特殊的线性规划和运输问题,正是由于其模型的特殊性,求解这类问题的方法才有其特殊的方法.
1.2 标准型的匈牙利解法
匈牙利法是库恩(W.W.Kuhn)于1955年提出的求解指派问题的算法,由于这种算法的理论根据是匈牙利数学家考尼格(D.Konig)提出的并证明了两个定理(证明略),因此得名匈牙利法.
1.2.1 匈牙利法基本思想
定理1设指派问题的系数矩阵为A=(aij)n×n,则从A的第i行各元素中分别减去一个常数ui(i=1,2,…,n),从第j列中各元素分别减去一个常数vj(j=1,2,…,n),得到一个新的效益矩阵B=(bij)n×n,其中bij=aij-(ui+vj)(i,j=1,2,…,n),那么以B为系数矩阵求得的最优解与原问题最优解相同.
定理2若一个方阵中的一部分元素为0,一部分非0,则覆盖方阵内所有0元素的最少直线数恰好等于那些位于不同行、不同列的0元素的最多个数.
匈牙利法的基本思想是:基于标准型(1),利用定理1不断变换效益矩阵,使其含有尽可能多的“0”元素,并且始终保持所有元素非负,直到能从变换后的矩阵中找到n个位于不同行、不同列的“0”元素(简称为独立0元素)为止.设最后得到的效益矩阵(bij)n×n,则以(aij)n×n为效益矩阵的指派问题与原问题同解.在(bij)n×n对应问题的解矩阵n×n中,对应这n个独立的0元素的变量xij取值为1,其他变量取值为0,则其目标函数值为0,它是最小值,从而得到以(bij)n×n为系数矩阵的指派问题的最优解,也是原问题的最优解.
1.2.2 匈牙利法的计算步骤
通过举例说明匈牙利法的具体步骤.
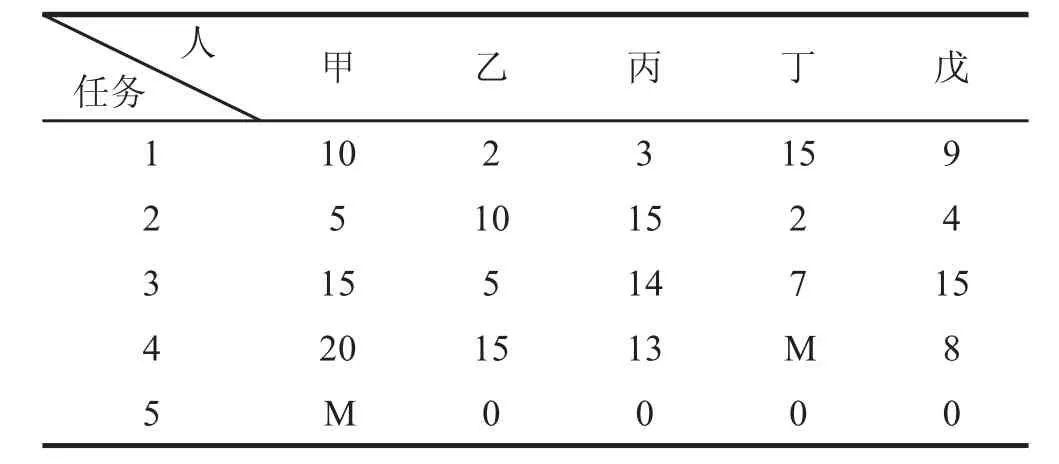
例1某任务有四项工作,需四个单位完成,因时间限制,每单位只能完成其中一项,单位Bj完成项目Ai所需时间如表1所示.

表1
求使总完成时间最少的分配方案.

第一步:效益矩阵的初始变换——0元素的获得
①从系数矩阵的每行元素减去该行的最小元素;
②再从系数矩阵的每列元素中减去该列的最小元素.
若某行(列)已有0元素,那就不必再减了,在例1中,

第二步:最优性检验
进行试指派,寻求最优解.为此,按以下步骤进行.
经第一步变换后,系数矩阵中每行每列都已有了0元素;但需找出n个独立的0元素,若能找出,解矩阵(xij)中,与这些独立0元素对应的元素xij为1,其他为0,这就得到最优解.当n较小时,可用观察法、试探法去找出n个独立0元素,若n较大时,就必须按一定的步骤去找,常用的步骤为:
①从只有一个0元素的行(列)开始,给这个0元素加圈,记作薜.这表示对这行所代表的人,只有一项任务可指派,然后划去薜所在的列(行)的其他0元素,记作准.这表示这列所代表的任务已派完,不必再考虑别人了.
②给出只有一个0元素列(行)的0元素加圈,记作薜,然后划去薜所在的行的0元素,记作准.
③反复进行①、②两步,直到所有0元素都被圈出或划掉为止.
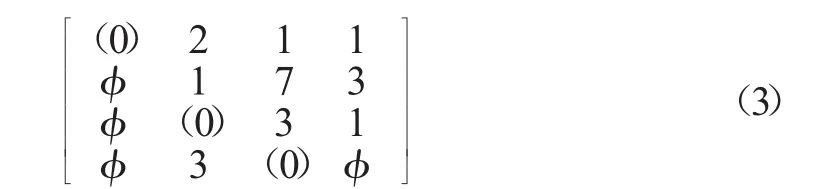
④若仍有没有划去的0元素,且同行(列)的0元素至少有两个(表示对这两项任务中指派其一,可用不同的方案去试探),从剩余的0元素最少的行(列)开始,比较这行各0元素所在列中0元素的数目,选择0元素少的那列的这个0元素加圈(表示选择性多的要让选择性少的),然后划掉同行同列的其他0元素,可反复进行,直到所有的0元素都已圈出和划掉为止.
对B进行①~④操作后得
⑤若薜元素的数目m等于矩阵的阶数n,那么指派问题的最优解已得到.若m 由于上面的矩阵中0元素的数目m=3 第三步:找出能覆盖非最优的变换阵中所有0元素的最少直线集合 即作最少的直线,覆盖所有的0元素,以确定该系数矩阵中能找到的最多的独立0元素数.按以下步骤进行: ①对无准的行打“√”号; ②对已打“√”号的行中所有含0元素的列打“√”; ③再对打“√”号的列中含有0元素的行打“√”; ④重复②、③直到得不到新的打“√”号的行、列为止; ⑤对未打“√”号的行画一横线,打“√”的列画一纵线,这就得到覆盖所有0元素的最少直线数.令这些直线数为l. 若l<n,说明必须再变换当前的系数矩阵,才能找到独立的0元素,为此转入第四步;若l=n,而m<n,应回到第二步中的④,另行试探. 本例中,对矩阵(3)按以下序次进行操作: 由于l=3 第四步:非最优阵的变换——0元素的移动 在未被直线覆盖的所有元素中,找出最小元素; 所有未被直线覆盖的元素都减去这个最小元素; 覆盖线十字交叉处元素都加上这个最小元素,其余元素不变. 即在没有被覆盖的元素中找出最小者,然后在打√列的各元素都加上这最小元素,以保证原来独立0元素不变,这样得到新系数矩阵(与原问题最优解相同).若得到n个独立0元素,则已得到最优解,否则重复第三步. 例1中,在(4)中找出(第一、第二行,第一列)未画线部分的最小元素为1,第一、二行各元素分别减去“1”,第一列各元素加“1”得矩阵(5) 由于出现未被划去的0元素,且所在行、列有多于一个0元素的,按第二步中的④的操作得 此时,矩阵(7)中,薜元素数目与直线数目相等,将(7)式中的薜元素换为“1”,其余元素换为“0”,则得到指派问题最优解 即x13=1,x21=1,x32=1,x44=1,其余xij=0,目标函数最优值: f*=39+31+41+39=150(小时) 匈牙利法只适用于指派问题的标准型,而实际的指派问题不一定是标准的,必须加以处理.针对目标函数是最大或最小、人数与任务数不等、定人定任务,提出了虚拟任务或人的方法,将问题转化为能够用匈牙利算法求解的等价指派问题.由于指派问题属于线性规划中的运输问题的特例,可以等价于线性规划和运输问题.此外,指派问题从对偶问题、对立问题的角度出发,也有等价问题,这些等价问题有的可转为标准型,有的不转标准型的方法也比较简单、易于计算,有很高的应用价值. 2.1 最大问题与最小问题的等价 当目标是极大化的指派问题时,即 则令:cij=M-aij,M充分大,以至于所有cij叟0(如取aij中的最大者为M),f=-Z,则上述问题可转化为极小指派问题: 且Zmax=nM-fmin 2.2 人数与任务数不等时虚增人或任务使得人数与任务数一致的等价 举例说明这种情况的处理. 例2某作战单位有三种火器拟分配给A、B、C、D四名射手,各射手使用不同的火器的命中概率如表2所示,问如何安排,使得总射击效果最好? 表2 解:设 令 该问题求最大值,先将极大化问题转化为极小化.取M=0.9,修正原效益矩阵 火器数比射手少1,增加一件虚拟火器M4,得效益矩阵 这样便得到一个标准指派问题模型,用匈牙利法求解,可得最优分配方案:第一种火器分配给B,第二种火器分配给A,第三种火器分配给D. 2.3 指定任务时的等价 n人n项工作,要求每人只能做一项工作,但指定某项工作必须由某人完成,问如何指派使完成任务的总时间最短? 例3分配甲、乙、丙、丁、戊去完成四项任务,每人完成各项任务的时间如表3.由于人多,规定其中有一任务可由两人共同完成,其中,丁不完成任务4,甲必须完成四项任务中的一项,试确定总花费时间最少的分派方案. 表3 虚增任务5,根据条件丁不完成任务3,甲必须完成四项任务中的一项,确定甲完成任务5的时间为很大值M,丁完成任务4的时间为M,在此基础上进行指派. 表4 这个问题和原问题等价.当然,虚增任务5,时间如下: 表5 在此基础上进行指派,根据定理1,这个问题也与原问题等价. 2.4 等价的对偶问题 在标准型指派问题匈牙利解法中,寻找独立0元素的个数最大值等价于寻找覆盖所有0元素的最少直线数,这就是对偶问题.对偶性体现在以下五个方面: (1)一个问题求最大值,另一个问题求最小值. (2)求最大值问题,约束条件为“=”,求最小问题,约束条件为“=”. (3)原问题中有n个变量,对偶问题就有n个约束条件,原问题有n个约束条件,对偶问题中就有n个变量(称为对偶变量). (4)原问题的目标函数中变量的系数就是对偶问题约束条件的常数项.原问题中约束条件的常数项就是对偶问题目标函数中变量的系数. (5)两个互为对偶问题约束条件的系数矩阵互为转置矩阵. 当找到了覆盖所有0元素的最少直线数等于独立0元素的个数(等于任务数和人数)时,即在直线上找到的不同行不同列的0元素,就是最优分配方案. 2.5 等价的对立问题 由于查找非标准型指派问题的最优分配方案,首先要进行标准型的转换,然后再利用匈牙利解法,多次循环,步骤较为繁琐.为了便于操作,我们可以考虑原指派问题的对立问题.对立问题就是通过梳理原问题(最小值)每行每列的(n-3)个对立(最大)值,在此基础上逐步找出最优分配方案.具体步骤如下: 第一步,若任务数和人数不一致,采用虚增任务或人转变为任务数和人数一致; 第二步,判断指派问题为最小问题还是最大问题,若为最小问题,则在费用矩阵中找最大值;若为最大问题,则在效益矩阵中找最小值; 第三步,判断矩阵的维度(设行列数为n,n>3),则需要找出对立深度为(n-3)的最值.当同一行或同一列除某元素外,皆为不同深度的最值,则该元素即为指派问题中一项最优解.重复以上过程,直至找出所有最优解.以例1为例. 对立深度4-3=1 Min问题等价于max问题,1c代表列最值,1r代表行最值, 在上面4×4的矩阵中,第二列除了40,第四列除了39外,这两列其余皆为不同深度的最值,根据对立等价性,第二列40与第四列39这两元素可能为最优解.通过比较这两个非深度最值,39较40更小,因此39为指派问题第四项任务的最优分配,划去39所在的行或列,在此基础上再用匈牙利法找出其它的最优解. 2.6 等价于运输问题 指派问题是一类特殊的运输问题,求解这类问题可等价于运输问题.即类似交通等情况,制定合理运输方案,使总的运输代价(运费或吨千米数)最小.运输问题可以用比单纯形法更有效的方法——表上作业法求解.建立运输图表;最小元素法寻求初始运输方案;用位势法判别初始运输方案是否最优;闭回路法寻求改进方案,回到第二步,计算改进方案检验数σ′ij.在求解运输问题过程中,有时会碰到非零数字格的个数小于m+n-1的情况,这时,在数字格中任选几个作为数字格,而使得数字格个数恰为m+n-1个,从而保证基变量个数为m+ n-1个,从而确定出最优分配方案. 2.7 等价于线性规划问题 指派问题是一类特殊的线性规划问题,求解这类问题可等价于线性规划问题,采用图解法,QSB软件法,单纯形法等方法寻找最优分配方案.在用图解法求解线性规划问题时可知,如果线性规划有最优解存在的话,则一定可以在可行域(凸多边形)的顶点上找到.这个方法可以推广到多个变量的线性规划问题.我们知道由多个变量所组成的不等式组成的可行域在n维空间内是一个凸多面体,与多边形一样,凸多面体的每一个顶点均是一个基本可行解.我们只需要从可行域(凸多面体)的顶点中去找,按照问题的标准形式,从可行域中一个基本可行解(一个顶点)开始,转换到另一个基本可行解(顶点),并且使目标函数的值逐步减少;当目标函数达到最小值时,问题就得到了最优解.当图解法使用困难时,可采用QSB软件法,单纯形法,matlab,lindo等方法. 以上给出了指派问题的七类等价问题,它们是从不同视角分析的等价问题,拓展了指派问题的寻优思路.七类等价问题虽然分类不同,但是它们之间有密切的关系,我们要根据每类问题的特点选择使用. 3.1 理顺各等价问题间的关系 指派问题问题按照是否标准分为标准型和非标准型两类,非标准型与标准型的转化就是一种大范围的等价,其中,最大最小问题的等价、任务数与人数不等、特定人员的指派问题都属于非标准型与标准型的等价问题,就是通过化非标准型为标准型,利用匈牙利法找出最优解.等价对偶问题是换一种思维方式寻找指派问题的分配方案,思维转换后再进行指派问题的分配.等价对立问题是从对立面思考,排除掉对立问题的方案,找出最优方案,这类问题在转型到任务数与人数一致的基础上,对任何指派问题可以直接寻找最优解,省去了很多中间步骤.指派问题是特殊的线性规划和运输问题,将指派问题等价于这两类问题也是自然.等价运输问题和等价线性规划问题,是从已有的运输问题和线性规划方法出发,寻找最优方案. 3.2 根据问题特点选择等价类型 指派问题的匈牙利法和等价于线性规划中的运输问题的方法适用于任务数和人数较小(小于等于4),当任务数和人数较多(大于4)时,可通过前三种等价问题,将非标准型指派问题转化为标准型来寻找最优分配方案.当对匈牙利法的两个定理很熟悉时,可以通过等价对偶问题,寻找覆盖所有0元素的最少直线数来判断最优分配方案.当指派问题基础知识掌握较好时,可以通过等价对立问题来进行最优分配. 3.3 利用不同类等价问题进行检验 以上七类等价问题都是原问题的等价问题,因此,它们之间可以进行相互检验.当手边有QSB软件包时,用指派问题等价于线性规划、运输问题、标准指派问题,查找最优方案,此时检验速度较快.当利用匈牙利法查找最优方案时,目测覆盖所有0的最少直线数等于任务数和人数,则将指派问题等价于对偶问题,选择对偶问题来进行寻找最优解的检验.当熟练掌握了指派问题及其解法,在采用等价于最大最小问题、人数任务数不同问题、独立0元素和覆盖0的直线数的对偶问题,找出最优解后,可以直接利用对立问题进行查找最优解检验. [1]张最良,李长生,张文志,等.军事运筹学[M].北京:军事科学出版社,2000. [2]董树军,张庆捷.军事运筹学教程[M].北京:蓝天出版社, 2006. The Research on Equivalence Problem of Assignment Problem BAO Pei-wen Assignment problems usually involve more than one solution.And the solutions concerned also involve smaller assignment problems,the amount of which is equivalent to the original problem.In other words,an original assignment has many equivalent problems.In this paper,in order to discuss the optimization of the assignment,the solutions of an assignment problem as well as its equivalent problems are analyzed.With the relations between solutions figured out, it would be more efficient for decision makers to pass down the assignment. assignment problem;equivalence problem;research O22 A 1671-9743(2017)05-0023-05 2016-12-28 鲍培文,1968年生,女,江西南昌人,教授,研究方向:军事运筹学、高等数学等.



2 指派问题的等价问题类型及其解法









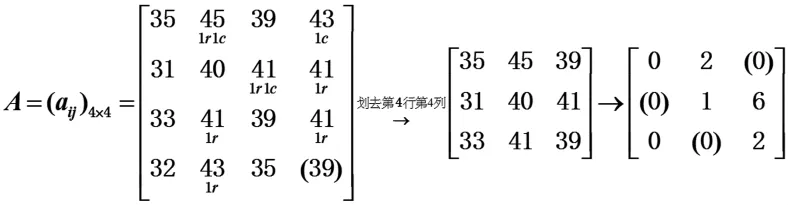
3 巧用等价问题求解时应把握的问题
(The Teaching and Research Department,Special Police College,Beijing,102211)
——如何培养学生的创新思维

