含有各阶导数的非线性4阶边值问题的正解

杨志林，李盟

（青岛理工大学理学院，山东青岛266033）

含有各阶导数的非线性4阶边值问题的正解

杨志林，李盟

（青岛理工大学理学院，山东青岛266033）

正解；先验估计；积分-常微分方程；Dirichlet问题；对称正解

1 引言

本文主要研究如下非线性4阶常微分方程边值问题的正解：

因而积累了丰富的文献，参见[1-13]，较早的文献见[14-18].作者在文[19]中研究了如下比（1.2）更一般的问题正解的存在性和唯一性：

其中αj，βj（j=0，1）为非负常数，且α0α1+α0β1+α1β0>0.得到的结果与2阶情形（即n=1）的结果类似[20，21].这些结果说明，由于具有对称性，Lidstone问题（1.2）和更一般的问题（1.3）本质上分别与2阶Dirichlet问题和Sturm-Liouville问题是一样的.自然地，人们希望知道非线性项依赖于各阶导数从而不再具有对称性的如下问题能有什么结果（这也是Eloe在[13]中提出的一个公开问题）：

这方面的文献不多，见[22]，相关的文章还见[23]及参考文献.本文将研究上述问题的一个类似问题（n=2），即研究如下问题的对称正解：

基本想法是先研究（1.1）的正解的存在性，然后再把所得结果应用于上述问题.为了克服各阶导数带来的困难，我们将问题（1.1）降阶转化为一个二阶积分-微分方程的边值问题.在先验估计的基础上，运用不动点指数理论建立这个二阶积分-微分方程的边值问题正解的存在性，多重正解的存在性以及正解的唯一性.

本文安排如下：第2节把问题（1.1）转化为一个二阶积分-微分方程的边值问题，并给出一些必要的引理；第3节叙述和证明本文的主要结果；第3节考虑问题（1.1）的一个特殊情形，即非线性项不含2阶导数的情形，得到了最优结果；第4节考虑问题（1.5）的对称正解.

2 问题的转化和引理

记

则（E，‖·‖）为实Banach空间，P为E中的锥.设

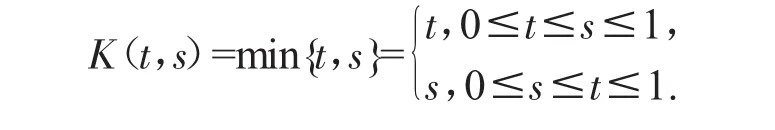
定义积分算子：

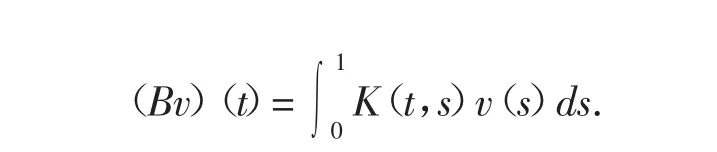
则B：E→E为全连续线性算子，而且是正线性算子，即B（P）奂P.令v（t）=-u″（t），则（1.1）等价于如下二阶积分-微分方程边值问题：

它又等价于如下积分-积分方程：

定义

若（H1）满足，则A：P→P全连续.从而（1.1）的可解性等价于全连续非线性算子A：P→P的不动点存在性问题.引理1设v∈C2[0，1]，v（0）=v′（1）=0，则

证分部积分，并利用v′（1）=0，可得到

再对第二个积分分部积分，并利用v（0）=0，得到

从而等式（2.3）成立.注意到（Bv）″=-v，坌v∈C[0，1]，根据引理1可得.引理2设v∈C[0，1]，则

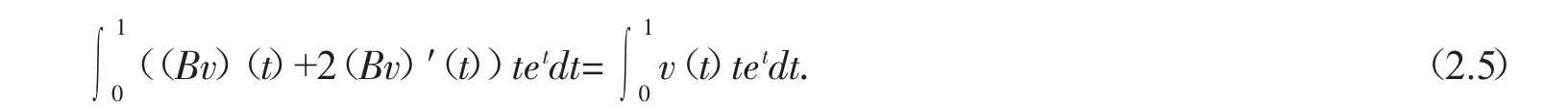
引理3设v∈P，v（0）=0，v′在[0，1]上递减，则

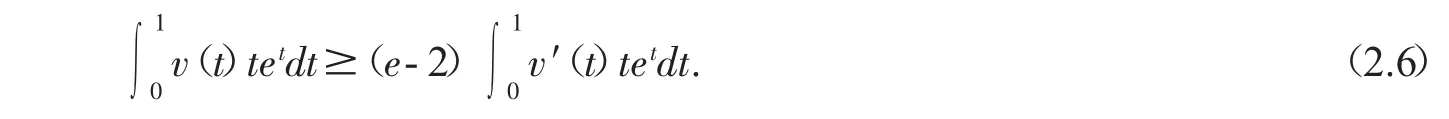
证由于v′在[0，1]上递减，tet在[0，1]上递增，并注意到v（0）=0，根据Chebyshev不等式，我们有

另一方面，注意到（1-t）et为[0，1]上递减函数，再根据Chebyshev不等式，得到

根据（2.4），我们有

联立上式和（2.7），即得不等式（2.6）.

引理4设v∈P，v（0）=0，则

证分部积分，并运用条件v（0）=0，可得

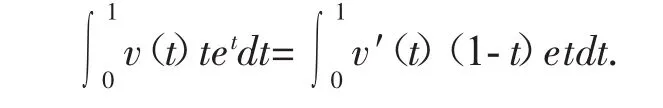
从而，

引理5[24]设E为实Banach空间，P为E中的正锥，Ω奂E为有界开集，A：Ω∩P→P全连续.若存在v0∈P {0}使得

则i（A，Ω∩P，P）=0，其中i为锥P上的不动点指数.

引理6[24]设E为实Banach空间，P为E中的正锥，Ω奂E为有界开集，0∈Ω.A：Ω∩P→P全连续.若

则i（A，Ω∩P，P）=1.

以下结果是容易证明的.

引理7对[0，1]上任何非负不恒为0的连续函数h，存在正数bh≥ah，使得

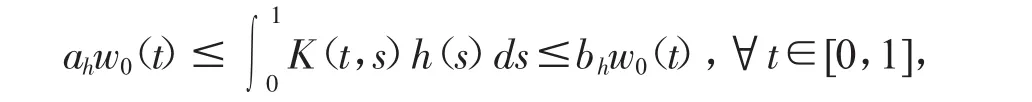
其中

3 正解的存在性：非线性项含有2阶导数的情形

本节讨论（1.1）正解的存在性以及多解的存在性，正解的唯一性.以下是本节使用的条件.

（H2）存在α叟0，β叟0，c>0，使得α（1-2e-1）+β>1，且

对任意（t，x1，x2，x3，x4）∈[0，1]×R+成立.

（H3）对任意M>0，存在函数Φ∈C（R+，R+）使得

（H4）存在a叟0，b叟0，r>0，使得a+b<1，且

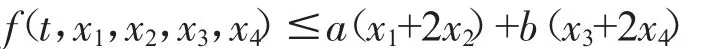
对任意（t，x1，x2，x3，x4）∈[0，1]×[0，r]×[0，r]×[0，r]×[0，r]成立.

（H5）存在ξ叟0，η叟0，c>0，使得ξ+η<1，且

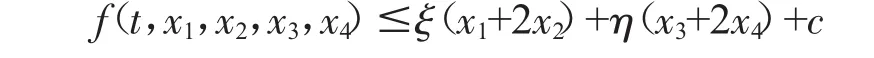
对任意（t，x1，x2，x3，x4）∈[0，1]×R4+成立.

（H6）存在p叟0，q叟0，r>0，使得p（1-2e-1）+q>1，且

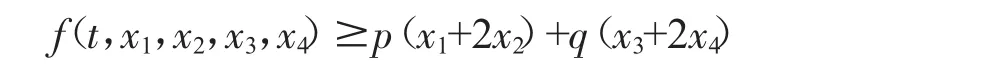
对任意（t，x1，x2，x3，x4）∈[0，1]×[0，r]×[0，r]×[0，r]×[0，r]成立.

（H7）存在ω>0，使得f在[0，1]×[0，ω]×[0，ω]×[0，ω]×[0，ω]上为x1，x2，x3，x4的增函数，且f（t，ω，ω，ω，ω）<ω，坌t∈[0，1].

（H8）f为x1，x2，x3，x4的增函数，且

对任意x1>0，x2>0，x3>0，x4>0，t∈[0，1]，λ∈（0，1）成立.

以下记Bρ={v∈E：‖v‖<ρ}，ρ>0.

定理1若（H1）-（H4）满足，则边值问题（1.1）至少有1个正解.

证明令

其中φ（t）=te-t.下证M1有界.事实上，若v∈M1，则v∈P∩C2[0，1]，v（0）=v′（1）=0，且存在μ≥0，使得

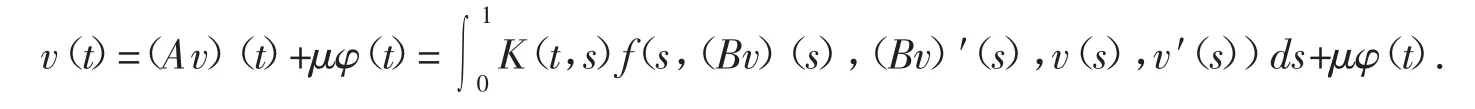
它等价于

根据（H2），我们有

上式中以ψ（t）=tet相乘，在[0，1]上积分，并注意到等式（2.3）和（2.5），得到

易知，对任意v∈M1，v′在[0，1]上递减，从而根据不等式（2.6），得到

从而

根据不等式（2.8），得到

由此进一步得到，对任意v∈M1，

另一方面，令

故存在M1>0，使得

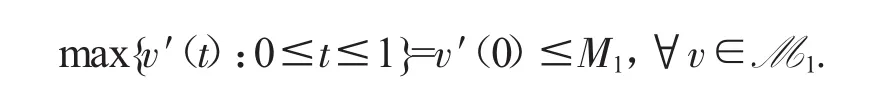
这说明M1有界.任取R>sup{||v||：v∈M1}，必有

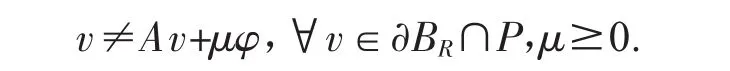
根据不动点指数的缺方向性（引理5），

下证M2＝{0}.事实上，若v∈M2，则，且存在θ∈[0，1]，使得

它的等价形式是

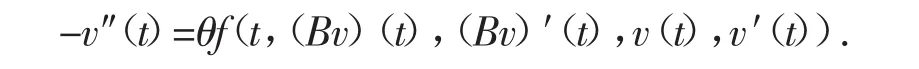
根据（H4），我们有

两边用ψ（t）=tet相乘，并注意到等式（2.3）和（2.5），得到

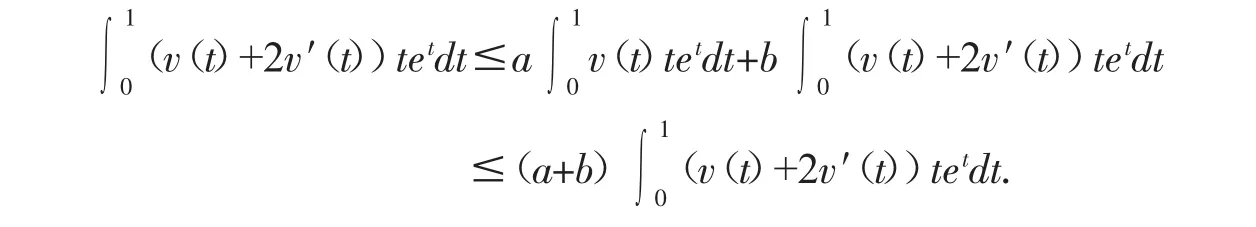
根据不动点指数的同伦不变性（引理6），

结合（3.4）（3.5），得到

定理2若（H1）（H5）（H6）满足，则边值问题（1.1）至少有1个正解.

证明令

下证M3为有界集.事实上，若u∈M3，则由定义知，v∈P∩C2[0，1]，v（0）=v′（1）=0，且存在λ∈[0，1]，使得

它等价于

根据（H5），我们有

两边用ψ（t）=tet相乘，并注意到等式（2.3），可得

从而，根据（2.8），得到

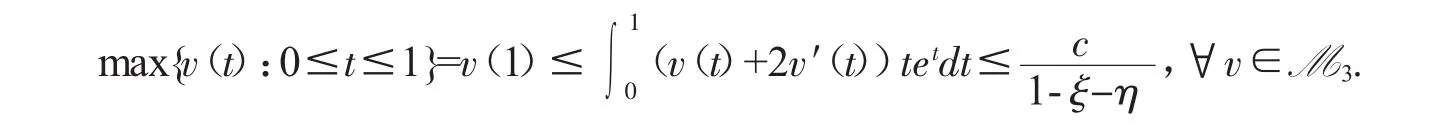
根据上式，更进一步，对任意v∈M3，我们有

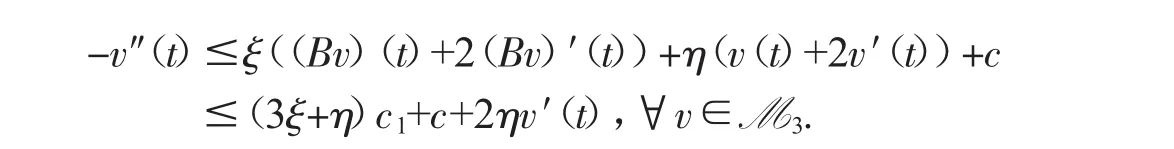
注意到v′（1）=0，由上式得到

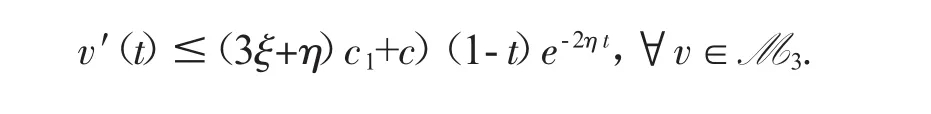
从而

这证明了M3的有界性.任取R>sup{‖v‖：v∈M3}，则必有

根据不动点指数的同伦不变性（引理6），

另一方面，令

其中φ（t）=te-t.下证M4={0}.事实上，若v∈M4，则v∈Br∩P∩C2[0，1]，v（0）=v′（1）=0，且存在λ叟0，使得

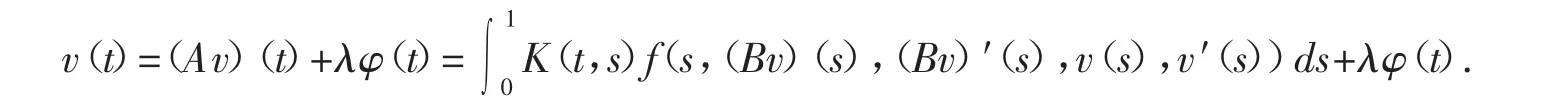
等价形式为

根据（H6），我们有

两边用ψ（t）=tet相乘，在[0，1]上积分，并注意到等式（2.3），得到

由于对任意v∈M4，v′在[0，1]上递减，从而根据不等式（2.6），得到

根据不动点指数的缺方向性（引理5），有

结合（3.6）（3.7）式，得到

故A在（BRBr）∩P上至少有一个不动点.从而边值问题（1.1）至少有一个正解.

定理3若（H1）（H2）（H3）（H6）（H7）满足，则边值问题（1.1）至少有2个正解.

证明根据（H2）（H3）（H6），可知（3.4）（3.7）成立，且可选取R>ω>r（参看定理1和定理2的证明）.根据（H9），

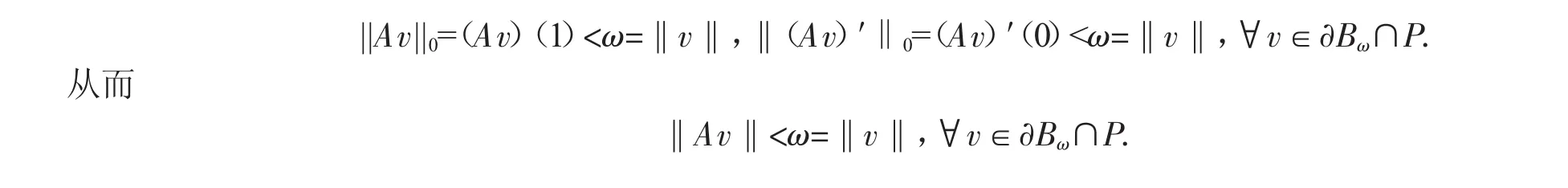
更进一步，有

根据不动点的同伦不变性（引理6），

再根据（3.4）（3.7），得到

所以A在（BRBω）∩P上和（BωB）r∩P上分别至少有1个不动点.从而边值问题（1.1）至少有2个正解.

定理4若（H1）（H5）（H6）（H8）满足，则边值问题（1.1）恰有1个正解.

证明根据定理2，边值问题（1.1）至少有1个正解，从而只需要证明正解的唯一性.设u1∈C4[0，1]，u2∈C4[0，1]为边值问题（1.1）的两个正解，则为算子A的两个正不动点，满足

根据引理7，存在ai>0，bi>0，使得

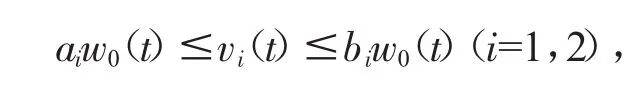
其中w0（t）由（2.9）给出.从而

令μ0=sup{μ>0：v2（t）叟μv1（t），坌t∈[0，1]}.则0<μ0<+∞.现在断言必有μ0叟1.否则0<μ0<1，令

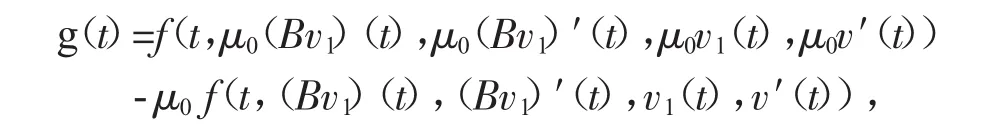
根据（H8），有g（t）>0，坌t∈（0，1）.从而根据引理7，存在ε>0，使得

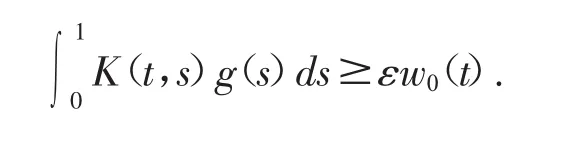
从而

这与μ0的定义矛盾.故μ0叟1，从而v2（t）叟μ0（t）叟v1（t），同理v1（t）叟v2（t）.故v1（t）≡v2（t），从而u1（t）≡u2（t）.所以边值问题（1.1）恰有1个正解.

4 正解的存在性：非线性项不含2阶导数的情形

本节我们考虑如下非线性项不含2阶导数u″的4阶边值问题正解的存在性问题：

其中非线性项f的条件如下：

对任意（t，x1，x2，x3）∈[0，1]×R3+成立.

（H11）对任意M>0，存在函数Φ∈C（R+，R+）使得

（H12）存在0<β<1，使得

对任意（t，x1，x2，x3）∈[0，1]×[0，r]×[0，r]×[0，r]成立.

（H13）存在00，使得

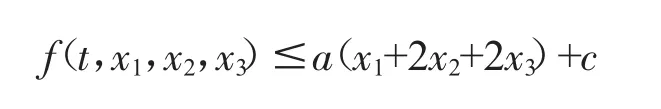
对任意（t，x1，x2，x3）∈[0，1]×R3+成立.

（H14）存在b>1，r>0，使得

对任意（t，x1，x2，x3）∈[0，1]×[0，r]×[0，r]×[0，r]成立.

根据引理1，可得到如下结果.

引理8若v∈C2[0，1]，v（0）=v′（1）=0，则

以下是本节的两个结果.

定理5若（H9）-（H12）满足，则边值问题（4.1）至少有1个正解.

定理6若（H9）（H13）（H14）满足，则边值问题（4.1）至少有1个正解.

运用引理8和第2节的有关引理，定理5和定理6的证明可仿照定理1和定理2的证明进行，故从略.还可以考虑（4.1）多重正解的存在性和正解的唯一性，限于篇幅，也从略.

注4.1可以看出，定理5和定理6给出了问题（4.1）正解存在的最佳条件.

5 Dirichlet问题的对称正解

本节我们应用主要结果来建立问题（1.5）对称正解的存在性，其中f满足如下条件：

（H15）f∈C（R+×R×R+×R，R+），f（x1，-x2，x3，-x4）=f（x1，x2，x3，x4），坌（x1，x2，x3，x4）∈R+×R×R+×R.

称u为（1.5）的对称正解，若u∈C4[.1，1]为（1.5）的解，且满足u（t）>0，坌t∈（-1，1），且u（-t）=u（t），坌t∈[-1，1].

定理7若（H15）（H2）（H3）（H4）满足，则（1.5）至少有1个对称正解.

证显然，（H15）可推出（H1）.于是，根据定理1，问题

至少有一个正解w.令

则u∈C4（[0，1]，R+）为（1.5）的一个对称正解.

类似可证明如下结果：

定理8若（H15）（H5）（H6）满足，则（1.5）至少有1个对称正解.

定理9若（H15）（H2）（H3）（H6）（H7）满足，则（1.5）至少有2个对称正解.

定理10若（H15）（H5）（H6）（H8）满足，则（1.5）恰有有1个对称正解.

[1]Y.Ma.Existence ofpositive solutions ofLidstone boundaryvalue problems[J].J.Math.Aanal.Appl，2006，314：97-108.

[2]Y.Wang.On 2nth-order Lidstone boundaryvalue problems[J].J.Math.Anal.Appl，2005，312：383-400.

[3]Y.Wang.On fourth-order elliptic boundaryvalue problems with nonmonotone nonlinear function[J].J.Math.Anal.Appl，2005，307：1-11.

[4]Z.Wei.Existenceofpositivesolutionsfor2nth-ordersingularsublinearbound-aryvalueproblems[J].J.Math.Anal.Appl，2005，306：619-636.

[5]Z.Wei.Positivesolutionsfor2nth-ordersingularsub-linearm-pointboundaryvalueproblems[J].AppliedMathematicsandComputation，2006，182：1280-1295.

[6]Z.Wei.A necessary and sufficient condition for 2nth-order singular superlinear m-point boundary value problems[J].J.Math.Anal.Appl，2007，327：930-947.

[7]Q.Yao.Existence of n positivesolutions to general Lidstone boundary value problems[J].Acta mathematica sinica，2005，48：365-376.

[8]R.P.Agarwal，D.O’Regan，S.Staněk.Singular Lidstone boundary value problem with given maximal values for solutions[J].Nonlinear Analysis，2003，55：859-881.

[9]Z.Bai，W.Ge.Solutions of 2nth Lidstone boundary value problems and de-pendence on higher order derivatives[J].J.Math.Anal.Appl，2003，279：442-450.

[10]J.M.Davis，P.W.Eloe，J.Henderson.Triple positive solutions and dependence on higher order derivatives[J].J.Math.Anal.Appl，1999，237：710-720.

[11]M.A.Del Pino，R.F.Manasevich.Existence for a fourth-order nonlinear boundary problem under a twoparameter nonresonance condition[J]. Proc.Amer.Math.Soc，1991，112：81-86.

[12]J.Ehme and J.Henderson.Existence and local uniqueness for nonlinear Lid-stone boundaryvalue problems[J].J.Inequ.Pure and Appl.Math，2000（1）：article 8.

[13]P.W.Eloe.Nonlinear eigenvalue problems for higher order Lidstone boundaryvalue problems[J].EJQTDE，2000（2）：1-8.

[14]A.R.Aftabizadeh.Existence and uniqueness theorems for fourth-order bound-ary value problems[J].J.Math.Anal.Appl，1986，116：415-426.

[15]R.P.Agarwal，On fourth-order boundaryvalue problems arisingin beamanalysis[J].Di.erential Integral Equations，1989（2）：91-110.

[16]R.P.Agarwal，G.Akrivis.Boundaryvalue problems occurringin plate defiec-tion theory[J].J.Comput.Appl.Math，1982，8：145-154.

[17]R.P.Agarwal，P.J.Y.Wong，Lidstone polynomials and boundaryvalue problems[J].Comput.Math.Appl，1989，17：1397-1421.

[18]C.DeCoster，C.Fabry，F.Munyamarere.Nonresonance conditions for fourth-order nonlinear boundary value problems[J].Int.J.Math.Math. Sci.，1994，17：725-740.

[19]Z.Yang.Existence and uniqueness of psoitive solutions for a higher or-der boundary value problem[J].Computers and mathematics with applications，2007，54：220-228.

[20]F.Li，Z.Liu.Multiple positive solutions ofsome operators and applica-tions[J].Acta Mathematica Sinica，Chinese Series，1998，41：97-102.

[21]Z.Liu，F.Li.Multiple positive solutions ofnonlinear two-point value problems[J].J.Math.Anal.Appl，1996，203：610-625.

[22]B.Zhang，X.Liu.Existence of multiple symmetric positive solutions of higher order Lidstone problems[J].J.Math.Anal.Appl，2003，284：672-689.

[23]H.Feng，D.Ji，W.Ge.Existence and uniqueness of solutions for a fourth-order boundary value problem[J].Nonlinear Analysis，2009，70：3561-3566.

[24]D.Guo，V.Lakshmikantham.Nonlinear problems in abstract cones[M].Academic Press，Boston，1988.

Positive Solutions of a Fourth-order Boundary Value Problem Involving all Derivatives

YANG Zhi-lin，LI Meng
（Department of Mathematics，Qingdao Technological University，Qingdao，Shandong 266033）

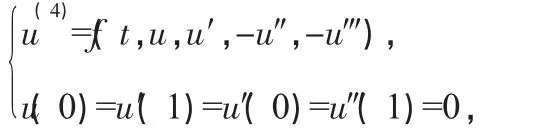
positive solution；a priori estimate；integro-ordinary differ-ential equation；dirichlet problem；symmetric positive solution

O175.8；O177.91

A

1671－9743（2017）05－0014－09

2016-11-09

山东省教育厅基金资助项目（J16LI09）.

杨志林，1963年生，男，湖南芷江人，教授，博士，研究方向：非线性泛函分析.